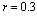-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Algorithms Research
p-ISSN: 2324-9978 e-ISSN: 2324-996X
2013; 2(2): 43-49
doi:10.5923/j.algorithms.20130202.02
Constant Stress Partially Accelerated Life Test Design for Inverted Weibull Distribution with Type-I Censoring
Mustafa Kamal, Shazia Zarrin, Arif-Ul-Islam
Department of Statistics & Operations Research, Aligarh Muslim University, Aligarh, 202002 (U.P.), India
Correspondence to: Mustafa Kamal, Department of Statistics & Operations Research, Aligarh Muslim University, Aligarh, 202002 (U.P.), India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In Accelerated Life Testing, acceleration factor is known or there exists a mathematical model which specifies the life stress relationship. However, there are some situations in which neither acceleration factor is known nor such models exist or are very hard to assume. In such cases partially accelerated life tests are better criterion to use. This paper deals with simple Constant Stress Partially Accelerated life test using type-I censoring. Assuming that the lifetimes of test item follow Inverted Weibull distribution, the maximum likelihood estimation procedure is used to obtain the estimates for the distribution parameters and acceleration factor. Asymptotic confidence interval estimates of the model parameters are also evaluated by using Fisher information matrix. A Simulation study is used to illustrate the statistical properties of the parameters and the confidence intervals.
Keywords: Acceleration Factor, Maximum Likelihood Estimation, Reliability Function, Fisher Information Matrix, Asymptotic Confidence Interval, Simulation Study
Cite this paper: Mustafa Kamal, Shazia Zarrin, Arif-Ul-Islam, Constant Stress Partially Accelerated Life Test Design for Inverted Weibull Distribution with Type-I Censoring, Algorithms Research , Vol. 2 No. 2, 2013, pp. 43-49. doi: 10.5923/j.algorithms.20130202.02.
Article Outline
1. Introduction
- In life testing and reliability experiments, time-to-failure data obtained under normal operating conditions is used to analyze the product’s failure-time distribution and its associated parameters. The continuous improvement in manufacturing design of today’s products and materials makes them highly reliable. Therefore, it is very difficult to obtain such life data while testing them at normal use conditions and the small time period between design and release. Under such conditions the life testing becomes very expensive and time consuming. These problems have motivated researchers to develop new life testing method and obtain timely information on the reliability of products, components and materials. Accelerated life testing (ALT) is then adopted and widely used in manufacturing industries. In ALT, products are tested at higher-than-usual levels of stress (e.g., temperature, voltage, humidity, vibration or pressure) to induce early failure. The life data collected from such accelerated tests is then analyzed and extrapolated to estimate the life characteristics under normal operating conditions by using a proper life stress relationship.A lot of literature is available for ALT analysis. For example, Nelson[1, 2] provides a bibliography of 159 references on statistical plans for accelerated tests. Shan-rang et al.[3] developed the statistical analysis method for obtaining estimators of the fouling life under usual stress level using type-II censored exponential life data under constant stress ALT models. Pascual[4] presents methods for planning ALT in the presence of k competing risks. Ding et al.[5] considers the design of ALT sampling plans under Type I progressive interval censoring with random removals. Tan et al.[6] proposed Bayesian method for analyzing incomplete data obtained from constant stress ALT when there are two or more failure modes, or competing failure modes. Ding and Tse[7] investigates the design of ALT plans under progressive Type II interval censoring with random removals assuming that the lifetimes of items follow a Weibull distribution, and the number of random removals at each inspection is assumed to follow a binomial distribution. Guo et al.[8] present two methods for designing ALT to compare two different designs in terms of their B10 life. Balakrishnan and Han[9] considered modification for censoring scheme in small sample sizes. Fan et al.[10] discussed the maximum likelihood estimation (MLE) and Bayesian inference in group data ALT models under the relationship between the failure rate and the stress variables is linear under Box-Cox transformation. Al-Masri and Al-Haj Ebrahem[11] derived the optimum times of changing stress level for simple step-stress plans under a cumulative exposure model assuming that the life time of a test unit follows a log-logistic distribution with known scale parameter by minimizing the asymptotic variance of the maximum likelihood estimator of the model parameters at the design stress with respect to the change time. Hassan and Al-Ghamdi[12] obtained the optimal times of changing stress level for simple stress plans under a cumulative exposure model using the Lomax. Xu and Fei[13] introduced and compared the four basic models for step-stress ALT: cumulative exposure model (CEM), linear cumulative exposure model (LCEM), tampered random variable model (TRVM), and tampered failure rate model (TFRM). Limitations of the four models were also discussed for better use of the models.There are situations where a life stress relationship is not known and cannot be assumed, i.e., the data obtained from ALT cannot be extrapolated to use conditions. In such situations, partially accelerated life testing (PALT) is used. In PALT, test units are run at both use and accelerated conditions. Constant stress PALT and step stress are two commonly used methods. In constant stress PALT products are tested at either normal use or accelerated condition only until the test is terminated. In step stress PALT, a sample of test items is first run at use condition and, if it does not fail for a specified time, then it is run at accelerated condition until a prespecified numbers of failures are obtained or a prespecified time has reached.So far a few research articles are available for constant stress PALT in which Bai & Chung[14] consider constant stress PALT to obtain maximum likelihood estimates of the parameter of the exponential distribution and the acceleration under type-I censoring, Abdel-Ghaly et al.[15] presented the MLE method to estimate the parameters of the Burr XII distribution with Types I and II censoring for a constant stress-PALT model, Abdel-Hamid[16] also considered the MLE method to estimate the parameters of the Burr XII distribution with progressive Type II censoring for a constant stress-PALT model, Ali A. Ismail[17] obtained the maximum likelihood estimators of the model parameters consider constant stress PALT with type-II censoring assuming that the lifetime at design stress has Weibull distribution. Cheng and Wang[18] present a model for constant-stress PALT for Burr XII distribution under multiple censored data. The performance of the MLEs of the parameters was obtained by two maximization methods. One is quasi-Newton algorithm and other is theexpectation-maximization (EM) algorithm. More recently Zarrin et al.[19] considered constant stress PALT with type-I censoring. Assuming Rayleigh distribution as the underlying lifetime distribution, the MLEs of the distribution parameter and acceleration factor were obtained.In this paper Constant Stress PALT plan using type-I censoring assuming that the lifetimes of test item at use condition follow an Inverted Weibull distribution is considered. Maximum likelihood estimates and confidence intervals for parameters and acceleration factor are obtained. The performance of the inference method used in present papers is evaluated by a simulation study.
2. The Model
- Notations: Some notations are used from Bai & Chung[14]
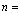 total number of test items in a PALT
total number of test items in a PALT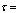 censoring time of in constant stress PALT
censoring time of in constant stress PALT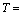 life time of an item at use condition
life time of an item at use condition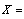 life time of an item at accelerated condition
life time of an item at accelerated condition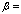 acceleration factor
acceleration factor 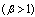 and defined as
and defined as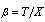
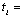 observed life time of
observed life time of 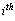 item at use condition
item at use condition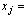 observed life time of
observed life time of 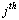 item at accelerated condition
item at accelerated condition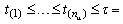 ordered failure times at use condition
ordered failure times at use condition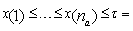 ordered failure times at accelerated conditionThe Inverted Weibull distributionThe probability density function (PDF), cumulative distribution function (CDF), reliability function (RF) and hazard function (HF) for Inverted Weibull distribution with scale parameter
ordered failure times at accelerated conditionThe Inverted Weibull distributionThe probability density function (PDF), cumulative distribution function (CDF), reliability function (RF) and hazard function (HF) for Inverted Weibull distribution with scale parameter 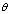 and shape parameter
and shape parameter 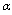 are given respectively by
are given respectively by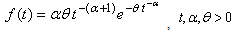 | (1) |
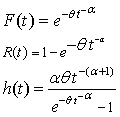 Constant Stress PALT Procedure:i. Total
Constant Stress PALT Procedure:i. Total 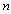 items are divided randomly into two samples of sizes
items are divided randomly into two samples of sizes 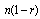 and
and 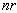 respectively where
respectively where 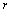 is sample proportion. First sample is allocated to normal use condition and other is assigned to accelerated conditions.ii. Each test item of every sample is run without changing the test condition until the censoring time
is sample proportion. First sample is allocated to normal use condition and other is assigned to accelerated conditions.ii. Each test item of every sample is run without changing the test condition until the censoring time 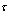 .Assumptions:i. At use condition the lifetime of a test item follows an Inverted Weibull distribution given in (1).ii. The lifetime of a test item at accelerated condition is obtained by using
.Assumptions:i. At use condition the lifetime of a test item follows an Inverted Weibull distribution given in (1).ii. The lifetime of a test item at accelerated condition is obtained by using 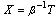 where
where 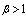 , is an acceleration factor. Therefore, the PDF at accelerated condition is given, for
, is an acceleration factor. Therefore, the PDF at accelerated condition is given, for 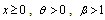 ,by
,by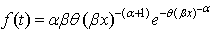 | (2) |
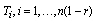 of items allocated to normal condition are i.i.d. random variables.iv. The lifetimes
of items allocated to normal condition are i.i.d. random variables.iv. The lifetimes 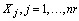 , of items allocated to accelerated condition are i.i.d. random variables.v. The lifetimes
, of items allocated to accelerated condition are i.i.d. random variables.v. The lifetimes 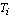 and
and 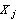 are mutually independent.
are mutually independent.3. Parameter Estimation
- The maximum likelihood estimation method is used here because the ML method is very robust and gives the estimates of parameter with good statistical properties such as consistency, asymptotic unbiased, asymptotic efficiency and asymptotic normality. In this method, the estimates of parameters are those values which maximize the sampling distribution of data. However, ML estimation method is very simple for one parameter distributions but its implementation in ALT is mathematically more intense and, generally, estimates of parameters do not exist in closed form, therefore, numerical techniques such as Newton Method and some computer programs are used to compute them.Let
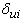 and
and 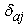 be the indicator functions (Indicator Function is a function defined on a set
be the indicator functions (Indicator Function is a function defined on a set 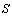 that indicates membership of an element in a subset
that indicates membership of an element in a subset 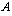 of
of 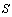 , having the value 1 for all elements of
, having the value 1 for all elements of 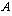 and the value 0 for all elements of
and the value 0 for all elements of 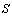 not in
not in 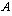 ) at use and accelerated condition respectively, such that
) at use and accelerated condition respectively, such that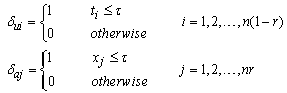 | (3) |
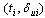 and
and 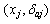 are respectively given by
are respectively given by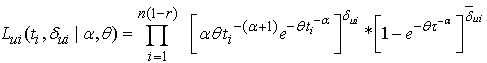 | (4) |
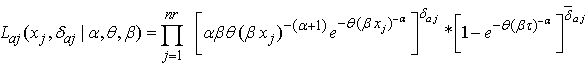 | (5) |
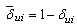 and
and 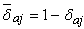 .The total likelihood for
.The total likelihood for 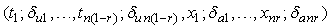 is given by
is given by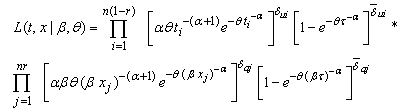 | (6) |
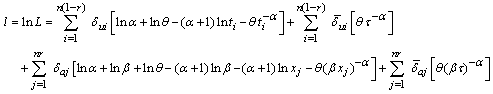 | (7) |
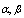 and
and 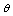 are obtained by solving the system of equations
are obtained by solving the system of equations 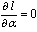 ,
, 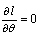 and
and 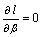 respectively, where
respectively, where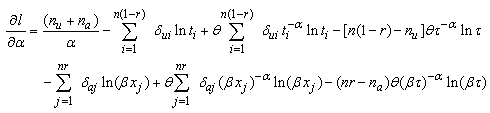 | (8) |
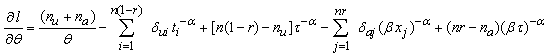 | (9) |
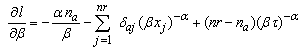 | (10) |
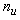 represent the number of items failed at use condition and is given by
represent the number of items failed at use condition and is given by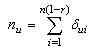
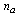 represent number of items failed at accelerated condition and is given by
represent number of items failed at accelerated condition and is given by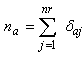 Equations (8), (9) and (10) are non-linear equations and in order to obtain the MLEs of
Equations (8), (9) and (10) are non-linear equations and in order to obtain the MLEs of 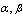 and
and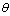 , their solutions will numerically be obtained by using Newton Raphson method.
, their solutions will numerically be obtained by using Newton Raphson method.4. Asymptotic Confidence Interval
- According to large sample theory, the maximum likelihood estimators, under some appropriate regularity conditions, are consistent and normally distributed. Since ML estimates of parameters are not in closed form, therefore, it is impossible to obtain the exact confidence intervals, so asymptotic confidence intervals based on the asymptotic normal distribution of ML estimators instead of exact confidence intervals are obtained here.The observed Fisher information matrix can be expressed in terms of the second derivative of the log likelihood function under the regularity conditions as:
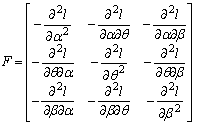 where elements of Fisher information matrix are given as
where elements of Fisher information matrix are given as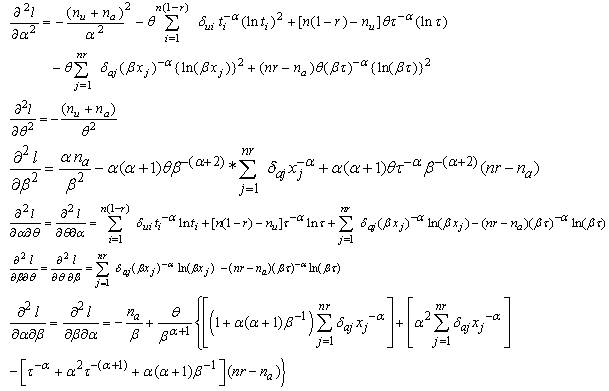 Now, the asymptotic variance-covariance matrix of
Now, the asymptotic variance-covariance matrix of  and
and can be written as
can be written as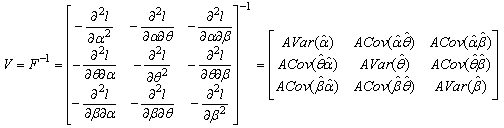 The
The 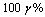 asymptotic confidence interval for of
asymptotic confidence interval for of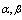 and
and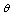 are then given respectively by
are then given respectively by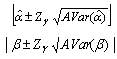 and
and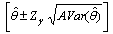
5. Simulation Study
- To evaluate the performance of the method of inference described in present study, first a random data with sample sizes
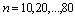 and censoring times
and censoring times 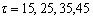 is generated from Inverted Weibull distribution. The values of parameters are chosen to be
is generated from Inverted Weibull distribution. The values of parameters are chosen to be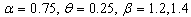 . The estimators and the corresponding summary statistics are obtained by the present Constant Stress PALT model. For different given samples and censoring times with
. The estimators and the corresponding summary statistics are obtained by the present Constant Stress PALT model. For different given samples and censoring times with 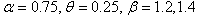 the ML estimates of, the asymptotic standard error
the ML estimates of, the asymptotic standard error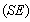 the mean squared error
the mean squared error 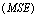 and the coverage rate of the 95% confidence interval for
and the coverage rate of the 95% confidence interval for 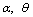 and
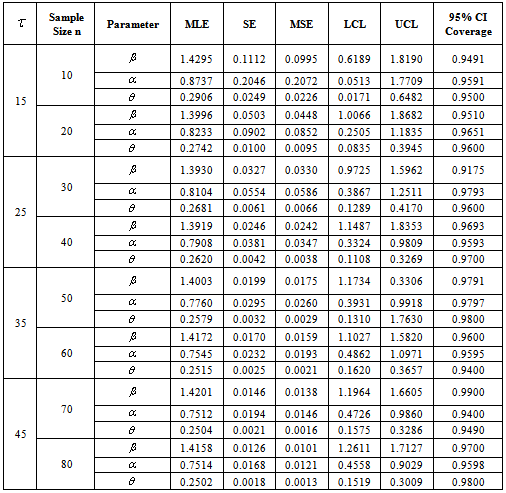
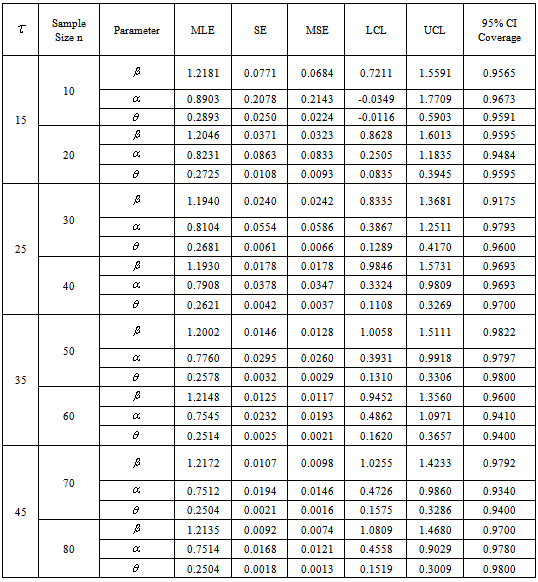
and 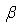 based on 500 simulation replications are obtained and summarized in Table-1 and 2.
based on 500 simulation replications are obtained and summarized in Table-1 and 2.
|
|
6. Conclusions
- From results in Table 1 and 2, it is observed that estimates obtained by the present model estimates the true parameters
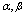 and
and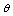 quite well respectively with relatively small mean squared errors. The estimated standard error also approximates well the sample standard deviation. For a fixed
quite well respectively with relatively small mean squared errors. The estimated standard error also approximates well the sample standard deviation. For a fixed 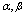 and
and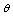 we find that as
we find that as 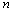 increases, the mean squared errors of the estimates get smaller. This may be because that a larger sample size results in a better large sample approximation. It is also observed that the mean squared errors of the estimates get smaller as τ increases for a fixed
increases, the mean squared errors of the estimates get smaller. This may be because that a larger sample size results in a better large sample approximation. It is also observed that the mean squared errors of the estimates get smaller as τ increases for a fixed 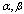 and
and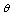 . It is also noticed that the coverage probabilities of the asymptotic confidence interval are close to the nominal level and do not change much across the different sample sizes. In short, it is reasonable to say that the present step stress ALT plan works well and has a promising potential in the analysis of accelerated life testing. For further future research in constant stress PALT one may consider some other life time distribution with different censoring schemes.
. It is also noticed that the coverage probabilities of the asymptotic confidence interval are close to the nominal level and do not change much across the different sample sizes. In short, it is reasonable to say that the present step stress ALT plan works well and has a promising potential in the analysis of accelerated life testing. For further future research in constant stress PALT one may consider some other life time distribution with different censoring schemes. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML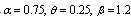 and
and 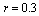
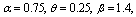 and
and