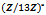-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Algorithms Research
p-ISSN: 2324-9978 e-ISSN: 2324-996X
2012; 1(5): 31-42
doi: 10.5923/j.algorithms.20120105.01
Cryptography: A Comparison of Public Key Systems
Tzvetalin S. Vassilev, Andrew Twizell
Department of Computer Science and Mathematics, Nipissing University, North Bay, Ontario, P1B 8L7, Canada
Correspondence to: Tzvetalin S. Vassilev, Department of Computer Science and Mathematics, Nipissing University, North Bay, Ontario, P1B 8L7, Canada.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Exchanging information electronically in a secure way become very important in the age of computers. Over fifty years of research and implementation were devoted to developing methods and systems for such a secure communication. These systems are commonly known as cryptosystems. Among the cryptosystems currently in use, the public key cryptosystems have a special place. These are cryptosystems which allow any user, completely unaware of the methods of encryption and decryption, i.e. of the intricate details of the system, to use them for variety of purposes in their daily life. The most common examples of this are digital signatures and electronic banking transactions. Here we provide an overview of different cryptosystems, including but not limited to an examination and comparison of five different influential public key cryptosystems. This examination includes an in-depth look at: the RSA algorithm, the Diffie-Hellman key exchange protocol, the elliptic curve cryptosystems, the ElGamal encryption method and the knapsack approach. We provide the necessary mathematical and number theoretic preliminaries. Further, we introduce each cryptosystem starting with the relevant definitions, theorems and properties. We discuss the encryption and the decryption process, the creation and exchange of the keys, present plenty of examples, as well as discussion of the implementation issues and the known strengths and weaknesses of each cryptosystem against cryptanalytic attacks.
Keywords: Cryptography, Public Key Cryptosystems, Algorithms, Elliptic Curves, RSA, Knapsack
Cite this paper: Tzvetalin S. Vassilev, Andrew Twizell, "Cryptography: A Comparison of Public Key Systems", Algorithms Research, Vol. 1 No. 5, 2012, pp. 31-42. doi: 10.5923/j.algorithms.20120105.01.
Article Outline
1. Introductory Mathematics
- Cryptography is the practise of creating techniques that allow the secure communication among two parties in the presence of eavesdroppers. Cryptography is a very old science dating back hundreds of years where its origins began with the very basic transposition ciphers, which would rearrange letters in words to form something else. Today it has become much more scientific with the design of cryptographic algorithms designed to be infeasible for an attacker to decipher. The purpose of the paper is to discuss the use of public key cryptosystems, describe and compare five major types of these systems. The five systems that will be discussed include: the RSA Cryptosystem, the Diffie-Hellman Key Exchange Protocol, the ElGamal Encryption Method, the Knapsack approach and the use of Elliptic Curves in Cryptosystems. Before these methods are discussed in detail, some introductory mathematics must first be established.
1.1. Greatest Common Divisor
- The first fundamentals of number theory that will be discussed are the concepts of greatest common divisor, divides and relatively prime. Consider the following definitions:Definition 1.1.1: Let a and b be two integers. We say that a divides b if there exists an integer k such that
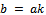 . We denote a divides b as:
. We denote a divides b as: 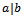 Definition 1.1.2: Let a and b be two integers. The greatest common divisor (gcd) of a and b, denoted by (a,b), satisfies the following two properties:•
Definition 1.1.2: Let a and b be two integers. The greatest common divisor (gcd) of a and b, denoted by (a,b), satisfies the following two properties:• 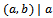 and
and 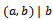 • If
• If 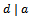 and
and 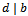 then
then 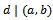 The concepts of divisibility and gcd are of the utmost importance when working with cryptosystems, specifically the ones mentioned in this paper. Definition 1.1.3: Let a and b be two integers. a and b are said to be relatively prime if and only if the only positive integer that divides both is 1, that is the gcd(a, b) = 1
The concepts of divisibility and gcd are of the utmost importance when working with cryptosystems, specifically the ones mentioned in this paper. Definition 1.1.3: Let a and b be two integers. a and b are said to be relatively prime if and only if the only positive integer that divides both is 1, that is the gcd(a, b) = 1 1.2. Congruence Modulo n
- The idea of division with remainders is one of the key components of most public key cryptosystems. Consider the following definition:Definition 1.2.1: Let a and b be two integers. We say that there is a remainder after division if there exist integers k and r such that
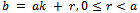 when r is the remainder. This definition ties perfectly into the idea of congruence modulo n, as defined by the following definition.Definition 1.2.2: Let a and b be two integers. a and b are said to be congruent modulo n. written:
when r is the remainder. This definition ties perfectly into the idea of congruence modulo n, as defined by the following definition.Definition 1.2.2: Let a and b be two integers. a and b are said to be congruent modulo n. written: 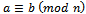 if they leave the same remainder on division by n. Equivalently, a is congruent to b, mod n if n divides a – b.It can also be said that a and b belong to the same congruence class, mod n. Example 1.2.1: Find three integers that are congruent to 5 (mod 13).Solution:By definition of congruence we need to find three integers a, b, c that are all congruent to 5 (mod 13).That is:
if they leave the same remainder on division by n. Equivalently, a is congruent to b, mod n if n divides a – b.It can also be said that a and b belong to the same congruence class, mod n. Example 1.2.1: Find three integers that are congruent to 5 (mod 13).Solution:By definition of congruence we need to find three integers a, b, c that are all congruent to 5 (mod 13).That is: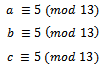 By definition of congruence mod n, 13 |(a – 5), Thus we can notice we have:
By definition of congruence mod n, 13 |(a – 5), Thus we can notice we have: 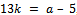 , thus
, thus 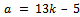 .Set
.Set 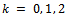 . We get
. We get 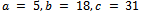 . Thus we have,
. Thus we have,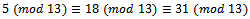 All these values belong to the same congruence class mod 13.
All these values belong to the same congruence class mod 13.1.3. Extended Euclidean Algorithm
- Using Definition 1.2.2 Euclid developed an algorithm to find the greatest common divisor by repeatedly subtracting the smaller number from the larger number. More precisely, his algorithm goes as follows:Suppose that
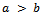 and let
and let 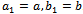 .Then for each pair
.Then for each pair 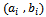 we form the pair
we form the pair 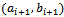 , where
, where 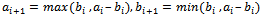 .Since this algorithm produces smaller and smaller pairs, eventually it must end and we notice that we will get:
.Since this algorithm produces smaller and smaller pairs, eventually it must end and we notice that we will get: 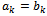 in which the case we conclude that
in which the case we conclude that 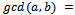
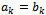 .Arguably the most important consequence of the Euclidean algorithm is that we have the following propositionProposition 1.3.1: Let a and b be integer values we can see from the Euclidean Algorithm that we have:
.Arguably the most important consequence of the Euclidean algorithm is that we have the following propositionProposition 1.3.1: Let a and b be integer values we can see from the Euclidean Algorithm that we have: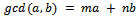 for some integers m and n.Example 1.3.1: Find the
for some integers m and n.Example 1.3.1: Find the 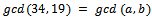 in the form
in the form 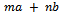 .Solution: We must begin by using division with remainder, subtracting the appropriate multiple of the second number from the first to get the remainder at each step. We have:
.Solution: We must begin by using division with remainder, subtracting the appropriate multiple of the second number from the first to get the remainder at each step. We have: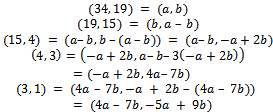 We can see that we now have,
We can see that we now have, 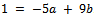 .We can try this out by substituting in our original values for a and b, we have
.We can try this out by substituting in our original values for a and b, we have 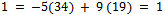 The Euclidean algorithm is extremely important in practice and theory. It is useful in practice because it is unusually fast, you can get the gcd of a k-digit number in around k steps, which is much faster than any known algorithm for finding divisors of a k-digit number.
The Euclidean algorithm is extremely important in practice and theory. It is useful in practice because it is unusually fast, you can get the gcd of a k-digit number in around k steps, which is much faster than any known algorithm for finding divisors of a k-digit number.1.4. Fast Exponentiation
- The next fundamental mathematical algorithm we must discuss is the process of computing large powers in a monoid G. This algorithm and its variants are central ingredients of many cryptographic protocols. We must begin by letting
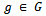 and e be a positive integer. Let
and e be a positive integer. Let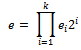 Be the binary expansion of e. Observe that the coefficients ei are either 0 or 1. Therefore,
Be the binary expansion of e. Observe that the coefficients ei are either 0 or 1. Therefore, 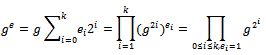 From this formula, we obtain the following idea for computing
From this formula, we obtain the following idea for computing 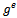 :1. Compute the successive squares
:1. Compute the successive squares 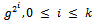 .2. Determine
.2. Determine 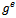 as the product of those
as the product of those 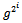 for which
for which 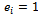 .Observe that
.Observe that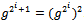 .Therefore,
.Therefore, 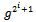 can be computed from
can be computed from 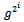 by squaring only once. Here is an example of a situation where this method is very useful.Example 1.4.1: Determine the value of 673 (mod 100).Solution: Consider
by squaring only once. Here is an example of a situation where this method is very useful.Example 1.4.1: Determine the value of 673 (mod 100).Solution: Consider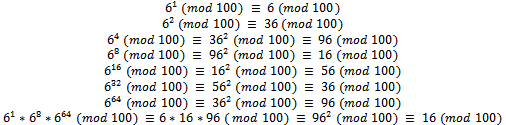 Note that using fast exponentiation only 6 squares were calculated and then the product of three integers (mod 100), compared to computing
Note that using fast exponentiation only 6 squares were calculated and then the product of three integers (mod 100), compared to computing 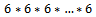 (with 73 calculations) then taking the modulus 100 of that value, this is a much easier computation.
(with 73 calculations) then taking the modulus 100 of that value, this is a much easier computation.2. RSA Cryptosystem
- The first public key cryptosystem invented was developed and named after its creators Ron Rivest, Adi Shamir and Len Adleman[9]. The RSA cryptosystem is a relatively strong security, and what makes it rather impressive is that since the system has been implemented in 1978 it still, to this day has not been broken[11]. To break the system a user must be able to factor a very large composite number which is the product of two large prime numbers.The RSA system is built on basic number theory, more specifically on (+, *) arithmetic modulo n, and on Fermat’s little theorem as generalized by Euler. The whole system works due to three simple properties of integers, well known by theoreticians:• It is difficult for a computer to factor a large number• It is easy for a computer to construct large prime numbers• It is easy for a computer to decide whether a given large number is prime
2.1. Generation of the Public Key
- To generate the public key we must begin with a few simple rules. Let us generate p, and q to be two large distinct prime numbers. Now we must find the product of p and q, and let n be this product, that is:
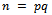 Now determine an integer e such that,
Now determine an integer e such that,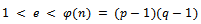 Where e is relatively prime to
Where e is relatively prime to 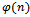 , that is
, that is 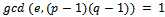 . It can be noted that e will always be odd, since
. It can be noted that e will always be odd, since 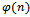 is always even, and if e was even then by definition of greatest common divisor,
is always even, and if e was even then by definition of greatest common divisor, 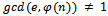 . We must now compute an integer d, such that:
. We must now compute an integer d, such that: 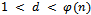 where
where 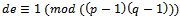 .The existence of this integer d is known from the simple fact that
.The existence of this integer d is known from the simple fact that 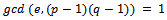 . Using the extended Euclidean algorithm we can determine a value d for every public key
. Using the extended Euclidean algorithm we can determine a value d for every public key 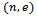 if the primes p and q are known. We call the value e the encryption exponent and our value d the decryption exponent.Example 2.1.1: Develop values p, q and use them to calculate the value n, and find encryption and decryption exponents that work with these values.Solution: Let our prime numbers be
if the primes p and q are known. We call the value e the encryption exponent and our value d the decryption exponent.Example 2.1.1: Develop values p, q and use them to calculate the value n, and find encryption and decryption exponents that work with these values.Solution: Let our prime numbers be 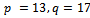 . We can easily compute that
. We can easily compute that 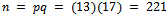 .It can easily be noticed that our
.It can easily be noticed that our 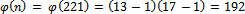 . Next we must determine an integer e such that
. Next we must determine an integer e such that 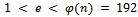 , and e is relatively prime to
, and e is relatively prime to 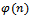 . We can use
. We can use 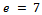 for this. It can easily be seen that
for this. It can easily be seen that 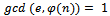 (which is the definition of relatively prime), and now we can use Euclid’s algorithm to find d:
(which is the definition of relatively prime), and now we can use Euclid’s algorithm to find d: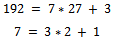 Working backwards, we can see that we have:
Working backwards, we can see that we have: 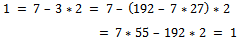 It can be noticed from this that we have:
It can be noticed from this that we have: 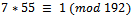 , thus giving us
, thus giving us 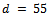 .
.2.2. Encrypting a Message Using the Public Key
- The encrypting of an integer is very simple using the RSA cryptosystem. Let our message that we wish to encrypt be called m, note that any
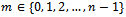 where m is relatively prime to n. To encode m using our public key
where m is relatively prime to n. To encode m using our public key 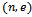 , we must compute:
, we must compute: 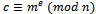 , where c is our desired ciphertext. We are now able to safely send our encoded value c to the receiver who has access to the decryption key d. For smaller values of
, where c is our desired ciphertext. We are now able to safely send our encoded value c to the receiver who has access to the decryption key d. For smaller values of 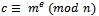 we can use the method discussed in Section 1.4 for fast exponentiation.Example 2.2.1: Encrypt the simple integer
we can use the method discussed in Section 1.4 for fast exponentiation.Example 2.2.1: Encrypt the simple integer 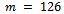 using the values computed in Example 2.1.1 so the message m is secure and cannot be decrypted without access to the decryption key d.Solution: We know from Example 2.1.1, we have the following values:
using the values computed in Example 2.1.1 so the message m is secure and cannot be decrypted without access to the decryption key d.Solution: We know from Example 2.1.1, we have the following values: 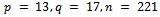 , where
, where 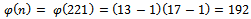 . We chose our value
. We chose our value 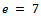 and calculated
and calculated 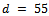 .Using the given integer
.Using the given integer 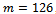 , we must use the public key
, we must use the public key 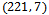 to calculate:
to calculate: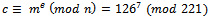 It can easily be seen that:
It can easily be seen that: 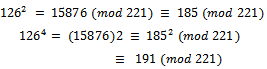 It can be seen that
It can be seen that 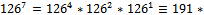
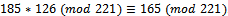 . It can be noted that our value for
. It can be noted that our value for 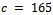 .
.2.3. Decrypting a Message Using the Decryption Key
- The decryption of RSA is based on the following theorem:Theorem 2.3.1: Let
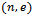 be a Public RSA key and d the corresponding private RSA key.Then:
be a Public RSA key and d the corresponding private RSA key.Then: 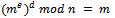 for any integer m with
for any integer m with 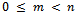 .Proof: We know that
.Proof: We know that 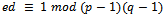 by the definition of d, thus there must exist an integer t such that
by the definition of d, thus there must exist an integer t such that 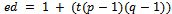 .Therefore
.Therefore 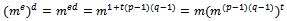 It follows that:
It follows that: 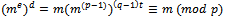 If p is not a divisor of m, then this congruence follows from Fermat’s little theorem (If
If p is not a divisor of m, then this congruence follows from Fermat’s little theorem (If 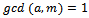 , then
, then 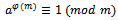 ). Otherwise, the assertion is trivial because both sides of the congruence are 0 (mod p). Analogously, we see that
). Otherwise, the assertion is trivial because both sides of the congruence are 0 (mod p). Analogously, we see that 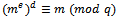 Because p and q are distinct prime numbers, we obtain
Because p and q are distinct prime numbers, we obtain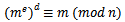 The assertion follows from the fact that
The assertion follows from the fact that 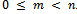 . This concludes the proof.Corollary 2.3.2: When the message m is encrypted by using
. This concludes the proof.Corollary 2.3.2: When the message m is encrypted by using 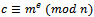 where
where 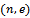 is the public key, it follows that the ciphertext c can be decrypted by the following equation:
is the public key, it follows that the ciphertext c can be decrypted by the following equation: 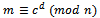 Thus using Corollary 2.3.2 we can now decrypt our ciphertext to find the original message m.Example 2.3.1: Decrypt the cipher text calculated in Example 2.2.1 using the values computed in Example 2.1.1 so the message m is recovered properly.Solution: We know from Examples 2.1.1 and 2.2.1 we have the following values:
Thus using Corollary 2.3.2 we can now decrypt our ciphertext to find the original message m.Example 2.3.1: Decrypt the cipher text calculated in Example 2.2.1 using the values computed in Example 2.1.1 so the message m is recovered properly.Solution: We know from Examples 2.1.1 and 2.2.1 we have the following values: 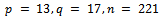 where
where 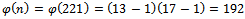 . We chose our value
. We chose our value 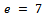 and calculated
and calculated 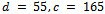 .Using Corollary 2.3.2, we can now decrypt our ciphertext
.Using Corollary 2.3.2, we can now decrypt our ciphertext 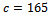 . We have:
. We have: 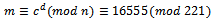 .Using the fast exponentiation as described in Section 1.4, we can see that:
.Using the fast exponentiation as described in Section 1.4, we can see that: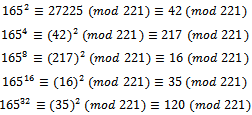 It can be noted that
It can be noted that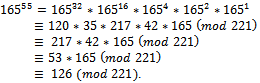 Thus we have decrypted our original message and found the desired result of
Thus we have decrypted our original message and found the desired result of 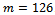 .
.2.4. Security of the RSA Cryptosystem
- The RSA cryptosystem is a public key system, thus to consider this a legitimate cryptosystem we must first consider the security of the system itself. More specifically we must consider the security of the secret key d. It can be noticed that for an attacker to compute the secret key directly, they will need to know the prime factorization of n, which gives them p and q. They use p and q with the public key to generate the value of d (by solving the congruence:
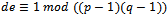 ), and decrypt any stolen message. The converse of this statement is also true, that it is possible to compute the values of p and q from the public key and the secret key. To show this, we must state the following lemma and theorems. First, we let
), and decrypt any stolen message. The converse of this statement is also true, that it is possible to compute the values of p and q from the public key and the secret key. To show this, we must state the following lemma and theorems. First, we let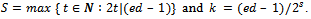 Theorem 2.4.1: Let
Theorem 2.4.1: Let 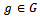 and
and 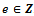 . Then
. Then 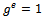 if and only if e is divisible by the order of g in G.Proof: Let
if and only if e is divisible by the order of g in G.Proof: Let 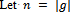 (the order of g). If
(the order of g). If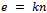 , then:
, then: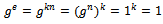 Conversely, let
Conversely, let 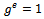 and
and 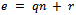 with
with 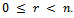 . Then:
. Then: 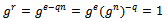 Because n is the least positive integer with
Because n is the least positive integer with 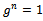 , and since
, and since 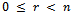 , we have
, we have 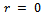 and therefore
and therefore  . Hence, n is a divisor of e, as asserted. This concludes the proof.Lemma 2.4.2: For all integers a that are relatively prime to n, the order of the residue class
. Hence, n is a divisor of e, as asserted. This concludes the proof.Lemma 2.4.2: For all integers a that are relatively prime to n, the order of the residue class 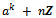 in the group
in the group 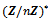 is in
is in 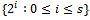 .Proof: Let a be an integer that is relatively prime to n. By Euler’s theorem we have
.Proof: Let a be an integer that is relatively prime to n. By Euler’s theorem we have 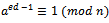 . Since
. Since 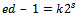 , this implies
, this implies 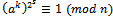 . Hence, by Lagrange’s theorem the order of
. Hence, by Lagrange’s theorem the order of 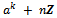 is a divisor of
is a divisor of 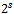 . This concludes the proof.Theorem 2.4.3: Let a be an integer that is relatively prime to n. If the orders of the residue class
. This concludes the proof.Theorem 2.4.3: Let a be an integer that is relatively prime to n. If the orders of the residue class 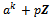 in
in 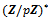 and for
and for 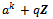 in
in 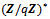 are different, then
are different, then 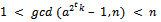 for some
for some 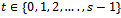 .Proof: By Lemma 2.4.2, the order of
.Proof: By Lemma 2.4.2, the order of 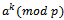 and
and 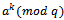 is in
is in 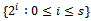 . Without loss of generality, the order of
. Without loss of generality, the order of  is greater than the order of
is greater than the order of 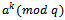 . Let the order of
. Let the order of  be
be 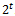 . Then
. Then 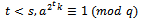 but
but 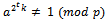 . Therefore,
. Therefore, 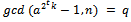 . This concludes the proof.Thus we can finally factor n, proceeding with the following algorithm:1. Choose at random an integer a in the set
. This concludes the proof.Thus we can finally factor n, proceeding with the following algorithm:1. Choose at random an integer a in the set 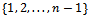 2. Compute
2. Compute 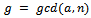 3. If
3. If 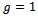 , then compute
, then compute 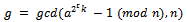 for
for 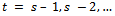 until g > 1 or t = 0.4. If
until g > 1 or t = 0.4. If 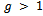 , then
, then 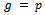 or
or 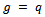 . Hence, the factorization of n is found and the algorithm terminates. Otherwise, the algorithm was unsuccessful with the chosen base.If the algorithm is not successful with the chosen a, then we run it again, therefore choosing a different base and starting over.Example 2.4.1: Let’s consider the following case: Let our prime numbers be
. Hence, the factorization of n is found and the algorithm terminates. Otherwise, the algorithm was unsuccessful with the chosen base.If the algorithm is not successful with the chosen a, then we run it again, therefore choosing a different base and starting over.Example 2.4.1: Let’s consider the following case: Let our prime numbers be 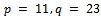 . We can easily compute that
. We can easily compute that 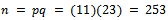 .It can easily be noticed that our
.It can easily be noticed that our 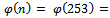
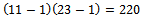 . Next we must determine an integer e such that
. Next we must determine an integer e such that 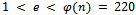 , and e is relatively prime to
, and e is relatively prime to 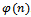 . We can use
. We can use 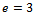 for this. It can easily be seen that
for this. It can easily be seen that 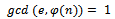 (which is the definition of relatively prime). We can use Euclid’s algorithm to find d:
(which is the definition of relatively prime). We can use Euclid’s algorithm to find d: 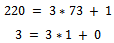 Working backwards, we can see that we have:
Working backwards, we can see that we have: 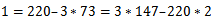 It can be noticed from this that we have:
It can be noticed from this that we have: 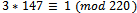 , thus giving us
, thus giving us 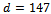 .Consider a situation where an attacker would like to factor n to find the primes p and q. They must know
.Consider a situation where an attacker would like to factor n to find the primes p and q. They must know 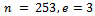 and
and 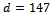 .Solution: It can be easily noted that ed=441-1=440. For the purpose of the algorithm we must select a base a in the set
.Solution: It can be easily noted that ed=441-1=440. For the purpose of the algorithm we must select a base a in the set 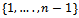 . For simplicity reasons, let us use
. For simplicity reasons, let us use 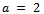 . We now can compute
. We now can compute 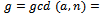
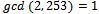 . Since our
. Since our 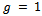 , we can move on to step 3, we must calculate
, we can move on to step 3, we must calculate 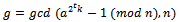 for
for 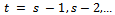 until
until 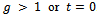 .Thus we have:
.Thus we have: 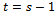 , this implies that
, this implies that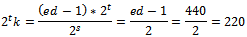 But
But 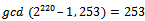 .So we try:
.So we try: 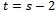 , this implies that
, this implies that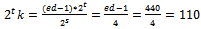 But
But 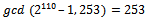 .So we try:
.So we try: 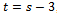 , this implies that
, this implies that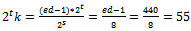 But
But 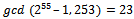 .Taking
.Taking 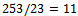 , thus the attacker has found our
, thus the attacker has found our 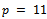 and
and 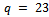 .Now that we have considered theoretical uses to the RSA Cryptosystem, we will consider a more practical use for the system.Example 2.4.2: A company approaches you to create a secure online ordering system. Your task is to create a system to securely transfer customer’s credit card information.Solution: It can be noted that every credit card number is 16 digits long, with 4 digits describing its expiry date, giving us 20 digits in total.For the purpose of this example we will use prime numbers of greater than 25 digits, yielding
.Now that we have considered theoretical uses to the RSA Cryptosystem, we will consider a more practical use for the system.Example 2.4.2: A company approaches you to create a secure online ordering system. Your task is to create a system to securely transfer customer’s credit card information.Solution: It can be noted that every credit card number is 16 digits long, with 4 digits describing its expiry date, giving us 20 digits in total.For the purpose of this example we will use prime numbers of greater than 25 digits, yielding 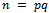 of roughly 50 digits in length. Let:
of roughly 50 digits in length. Let: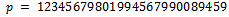 and
and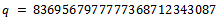 This gives
This gives And
And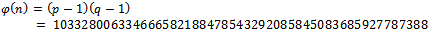 Next we must determine an integer e such that
Next we must determine an integer e such that 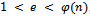 , and e is relatively prime to
, and e is relatively prime to 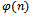 . We can use
. We can use 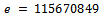 for this. It can be seen that
for this. It can be seen that 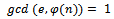 (which is the definition of relatively prime).We now must determine an integer d such that
(which is the definition of relatively prime).We now must determine an integer d such that 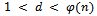 such that
such that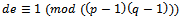 . Our values are much too large to use the Euclidean Algorithm or any sort of trial an error method, although it can be calculated that our d would be:
. Our values are much too large to use the Euclidean Algorithm or any sort of trial an error method, although it can be calculated that our d would be: This cryptosystem is constrained to only send messages m that are relatively prime to n. Although, the only divisors of n are at least 25 digits long, and as mentioned above credit card numbers will only be of length 16 digits + 4 digits for the expiry date.Consider a customer with a credit card number of 4540 3204 4567 8231 1002 with an expiry date of 10/02. This gives us an m of:
This cryptosystem is constrained to only send messages m that are relatively prime to n. Although, the only divisors of n are at least 25 digits long, and as mentioned above credit card numbers will only be of length 16 digits + 4 digits for the expiry date.Consider a customer with a credit card number of 4540 3204 4567 8231 1002 with an expiry date of 10/02. This gives us an m of: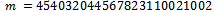 Thus we can calculate (encrypt) the message as follows:
Thus we can calculate (encrypt) the message as follows: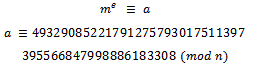 We can see that this message has been safely transmitted without the worry of being broken (unless someone knows the secret key, d)Upon receiving the encrypted message, we can easily calculate the original message using the following equivalency:
We can see that this message has been safely transmitted without the worry of being broken (unless someone knows the secret key, d)Upon receiving the encrypted message, we can easily calculate the original message using the following equivalency: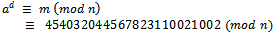 Note: Although the values of p and q were seemingly very large, it should be considered that a computer could easily factor n of only roughly 50 digits. Thus leaving the encrypted message unprotected.
Note: Although the values of p and q were seemingly very large, it should be considered that a computer could easily factor n of only roughly 50 digits. Thus leaving the encrypted message unprotected.3. Diffie-Hellman Key Exchange
- The Diffie-Hellman key exchange was first established in 1976 during a collaboration between its creators Whitfield Diffie and Martin Hellman[12]. It was the first practical method for establishing a shared secret over an unprotected communications channel. It was considered the first major milestone in public key cryptography[13]. Before we can begin exploring the Diffie-Hellman key exchange we must first look at discrete logarithms:
3.1. Discrete Logarithms
- Definition 3.1.1: Let p be a prime number, we know that the group
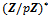 is cyclic of order
is cyclic of order 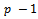 . Let g be primitive root
. Let g be primitive root 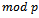 . (g is a generator of the multiplicative group of residues
. (g is a generator of the multiplicative group of residues 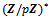 ). That is: Let A be the set
). That is: Let A be the set 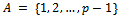 . We know that for all
. We know that for all 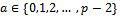 with
with 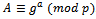 .The exponent a is referred to as the discrete logarithm of A to the base g. It can be written as:
.The exponent a is referred to as the discrete logarithm of A to the base g. It can be written as: 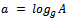 . Since the computation of discrete logarithms is considered to be difficult no efficient algorithm for solving the problem is known.Example 3.1.1: Choose a prime number and show one of its primitive roots. Solution: Let
. Since the computation of discrete logarithms is considered to be difficult no efficient algorithm for solving the problem is known.Example 3.1.1: Choose a prime number and show one of its primitive roots. Solution: Let 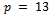 . A primitive root modulo 13 is 6. Below we will show that 6 is primitive root of 13 by computing the discrete logarithms of all integers in
. A primitive root modulo 13 is 6. Below we will show that 6 is primitive root of 13 by computing the discrete logarithms of all integers in 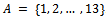 .We can see that we have:
.We can see that we have:
|
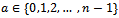 with
with 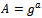 .
.3.2. The Diffie Hellman Key Exchange
- The Diffie-Hellman key exchange is used for a specific reason, two people let’s say Alice and Bob would like to agree on a secret key, but their only means of communication is over an unsecured channel.The first step is for Alice and Bob to agree on a large prime number p and an integer g with
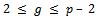 such that the order of
such that the order of 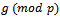 is sufficiently large. The prime p and the primitive root g can be publicly known. Thus using the unsecured channel won’t be a problem for Alice and Bob.The next step of the Diffie-Hellman Key exchange, Alice choose an integer
is sufficiently large. The prime p and the primitive root g can be publicly known. Thus using the unsecured channel won’t be a problem for Alice and Bob.The next step of the Diffie-Hellman Key exchange, Alice choose an integer 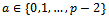 and computes:
and computes: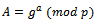 This result A is sent to Bob, but Alice keeps the exponent a secret. Bob follows the same step choosing an integer
This result A is sent to Bob, but Alice keeps the exponent a secret. Bob follows the same step choosing an integer 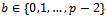 and computes:
and computes: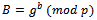 This result B is sent to Alice, keeping his exponent b secret. For both to obtain the secret key they compute the following:Alice:
This result B is sent to Alice, keeping his exponent b secret. For both to obtain the secret key they compute the following:Alice: 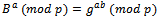 Bob:
Bob: 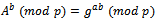 Thus, the secret key is known by both parties, but no one listening on the unsecured network can compute what Bob and Alice chose for their secret key.Secret key:
Thus, the secret key is known by both parties, but no one listening on the unsecured network can compute what Bob and Alice chose for their secret key.Secret key: 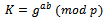
3.3. The Selection of p and q
- It can be noted that the selection of p and g should be chosen so that the computation of the integer g has an order (mod p) that is sufficiently high. That is: By definition of order, let n be the smallest positive integer such that
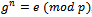 , where e is the identity element. We want the integer n to be sufficiently large, so an attacker cannot easily compute it. As mentioned above, one possibility is to choose g as a primitive root
, where e is the identity element. We want the integer n to be sufficiently large, so an attacker cannot easily compute it. As mentioned above, one possibility is to choose g as a primitive root 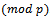 . However to compute a primitive root of p, you must find the prime factorization of p-1. Since p should be a large prime number, finding this prime factorization should be very difficult. Which leads to the fact that selecting a primitive root of a large prime p, is also in fact very difficult. Selecting a prime p of a special form that is a prime p where
. However to compute a primitive root of p, you must find the prime factorization of p-1. Since p should be a large prime number, finding this prime factorization should be very difficult. Which leads to the fact that selecting a primitive root of a large prime p, is also in fact very difficult. Selecting a prime p of a special form that is a prime p where 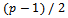 is also a prime number. This makes it easier to find a primitive root g of p.Example 3.3.1: Show how two people can exchange a secret key K over an unsecured channel.Solution: Consider Alice and Bob want to share a message over an open channel, they agree on a prime number, say
is also a prime number. This makes it easier to find a primitive root g of p.Example 3.3.1: Show how two people can exchange a secret key K over an unsecured channel.Solution: Consider Alice and Bob want to share a message over an open channel, they agree on a prime number, say 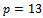 and a primitive root (or base) say
and a primitive root (or base) say 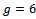 . (For the purpose of this example we will use small values for p and g.)Alice chooses
. (For the purpose of this example we will use small values for p and g.)Alice chooses 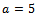 to be her exponent and computes
to be her exponent and computes 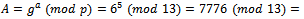
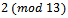 . Alice then sends this value
. Alice then sends this value 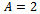 to Bob.Bob chooses
to Bob.Bob chooses 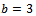 to be his exponent and computes
to be his exponent and computes 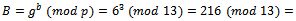
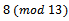 . Bob then sends this value
. Bob then sends this value 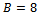 to Alice.Once both parties receive their values, they compute their secret key:Alice:
to Alice.Once both parties receive their values, they compute their secret key:Alice: 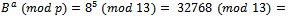
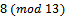 Bob:
Bob:  Thus the secret key is 8.
Thus the secret key is 8.3.4. The Diffie Hellman Problem and the Discrete Logarithm Problem
- Definition 3.4.1: Let G be a finite cyclic group generated by an element g. The problem of computing
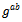 from
from 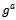 and
and 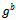 where a and b are the secret values Alice/Bob choose. This is called the Diffie–Hellman Problem (DH problem) with respect to g.Definition 3.4.2: Let G be a finite cyclic group generated by an element g. The problem of computing from
where a and b are the secret values Alice/Bob choose. This is called the Diffie–Hellman Problem (DH problem) with respect to g.Definition 3.4.2: Let G be a finite cyclic group generated by an element g. The problem of computing from 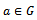 a number s such that
a number s such that 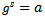 is called the discrete logarithm problem (DL problem) with respect to g.It can be noticed that if someone can solve the discrete logarithm problem for p they can immediately solve the Diffie–Hellman problem. The converse is not known. That is, it is thought to be possible (highly unlikely) that someone could invent a way to solve the Diffie–Hellman problem without being able to find discrete logarithms.To use the discrete logarithm problem to solve the DH problem, the attacked can determine the discrete logarithm b of B to the base g and compute the key
is called the discrete logarithm problem (DL problem) with respect to g.It can be noticed that if someone can solve the discrete logarithm problem for p they can immediately solve the Diffie–Hellman problem. The converse is not known. That is, it is thought to be possible (highly unlikely) that someone could invent a way to solve the Diffie–Hellman problem without being able to find discrete logarithms.To use the discrete logarithm problem to solve the DH problem, the attacked can determine the discrete logarithm b of B to the base g and compute the key 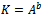 .Definition 3.4.3: A Diffie–Hellman oracle (DH oracle for short) for a group G with respect to a given generator g takes as inputs two elements
.Definition 3.4.3: A Diffie–Hellman oracle (DH oracle for short) for a group G with respect to a given generator g takes as inputs two elements 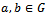 (where
(where 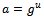 and
and 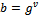 ) and returns (without computational cost) the element
) and returns (without computational cost) the element 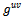 .It can be shown that under a plausible but unproven number theoretic assumption, for every finite cyclic group whose order is not divided by a multiple large prime factor there exists a polynomial-time algorithm for computing discrete logarithms and that makes calls to a DH oracle for this group.Definition 3.4.4: For
.It can be shown that under a plausible but unproven number theoretic assumption, for every finite cyclic group whose order is not divided by a multiple large prime factor there exists a polynomial-time algorithm for computing discrete logarithms and that makes calls to a DH oracle for this group.Definition 3.4.4: For 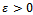 , an
, an 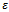 -DH-oracle is a probabilistic oracle which returns for an input
-DH-oracle is a probabilistic oracle which returns for an input 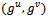 the correct answer
the correct answer 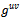 with probability at least
with probability at least 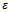 if the input is uniformly distributed over
if the input is uniformly distributed over 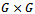 . The offset of the oracle’s answer is
. The offset of the oracle’s answer is 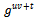 to the input
to the input 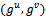 is defined as
is defined as 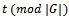 . A translation – invariant
. A translation – invariant  -DH-oracle is an
-DH-oracle is an  -DH-oracle whose offset distribution is the same for every
-DH-oracle whose offset distribution is the same for every 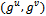 .
.4. Elliptic Curve Cryptosystems
- The use of elliptic curves in cryptography was first proposed by Neal Koblitz[17] and Victor Miller[18] in 1985. Elliptic curves can be defined over any field, but for the purpose of cryptography only finite fields are of interest. The size of the elliptic curve determines the difficulty of an attacker discovering the user’s secret key. Advantages of using an elliptic curve public key cryptosystem compared to another public key system, such as the RSA Algorithm, is that elliptic curves are much more efficient then RSA that is the calculations are much smaller[19]. The idea that RSA may one day become insecure, or at least the key sizes needed to safely secure a message become too large, it is believed that the elliptic curve cryptosystem may prove to be a very good alternative. Although there are disadvantages to using an elliptic curve cryptosystem, mainly group operations on elliptic curves are more complicated than group operations in prime fields.
4.1. Elliptic Curves
- An introduction to elliptic curves is necessary before the discussion of elliptic curves use in public key cryptosystems. There is extensive literature on elliptic curves as they arise naturally in many branches of mathematics and are closely linked with the theory of elliptic functions, where of course they get their name. Consider the following definitions:Definition 4.1.1: A ring R is a set with two binary operations, addition (denoted by
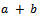 ) and multiplication (denoted by ab), such that for all
) and multiplication (denoted by ab), such that for all 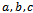 in R:1.
in R:1. 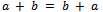 2.
2. 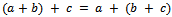 3. There is an additive identity 0. That is, there is an element 0 in R such that
3. There is an additive identity 0. That is, there is an element 0 in R such that 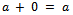 for all a in R.4. There is an element
for all a in R.4. There is an element 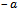 in R such that
in R such that 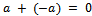 .5.
.5. 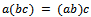 6.
6. 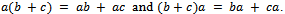 A ring is an Abelian group under addition, also having associative multiplication that is left and right distributive over addition. When multiplication is commutative we say that the ring is commutative. When a ring has an identity under multiplication we say that the ring has unity. Unity is a nonzero element that is an identity under multiplication.Definition 4.1.2: A field F is a commutative ring with unity in which every nonzero element is a unit. A unit of a ring is a nonzero element that has a multiplicative inverse.Definition 4.1.3: Let E be an elliptic curve over a field F, E is a curve that is given by an equation of the form:
A ring is an Abelian group under addition, also having associative multiplication that is left and right distributive over addition. When multiplication is commutative we say that the ring is commutative. When a ring has an identity under multiplication we say that the ring has unity. Unity is a nonzero element that is an identity under multiplication.Definition 4.1.2: A field F is a commutative ring with unity in which every nonzero element is a unit. A unit of a ring is a nonzero element that has a multiplicative inverse.Definition 4.1.3: Let E be an elliptic curve over a field F, E is a curve that is given by an equation of the form: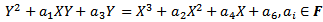 We let
We let 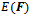 denote the set of points
denote the set of points 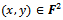 that satisfy this equation, along with a point of infinity, denoted by O. For the purpose of this paper, only elliptic curves over prime fields will be considered.Definition 4.1.4: Let p be a prime number,
that satisfy this equation, along with a point of infinity, denoted by O. For the purpose of this paper, only elliptic curves over prime fields will be considered.Definition 4.1.4: Let p be a prime number, 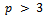 and let
and let 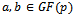 . Consider the equation:
. Consider the equation: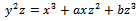 Its discriminant is:
Its discriminant is: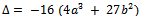 It can be assumed that the discriminant is non-zero. If
It can be assumed that the discriminant is non-zero. If 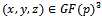 is a solution of this equation, then for any
is a solution of this equation, then for any 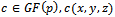 is also a solution. Two solutions
is also a solution. Two solutions 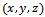 and
and 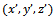 are called equivalent if there is a non-zero
are called equivalent if there is a non-zero 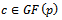 with
with 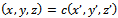 The equivalence class of
The equivalence class of 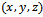 is denoted by
is denoted by 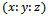 . The elliptic curve
. The elliptic curve 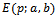 is the set of all equivalence classes of solution of
is the set of all equivalence classes of solution of 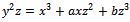 . Each point of the curve is an element of this set.Example 4.1.1: Consider the field
. Each point of the curve is an element of this set.Example 4.1.1: Consider the field 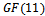 . Over this field, consider the equation
. Over this field, consider the equation 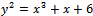 . Find the set of all solutions of this curve.Solution: We can see that we have
. Find the set of all solutions of this curve.Solution: We can see that we have 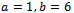 and
and 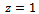 . The discriminant is
. The discriminant is 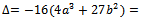
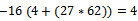 . Thus we can see that
. Thus we can see that 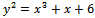 defines an elliptic curve over
defines an elliptic curve over 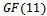 . It is:
. It is: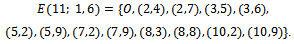
4.2. Elliptic Curves in Cryptography
- Elliptic Curve Diffie-Hellman (ECDH) is a key agreement protocol that allows two parties, each having an elliptic curve public-private key pair, to establish a shared secret over insecure channel. This shared secret key may be directly used as a key, or better yet, to derive another key which can be used to encrypt a message using a symmetric key cipher.
4.3. Key Establishment Protocol
- Suppose Alice wants to establish a shared key with Bob, but the only channel available for them may be unsecure. Initially, the domain parameters (that is,
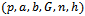 in the prime case or
in the prime case or 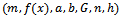 in the binary case) must be agreed upon. Also, each party must have a key pair suitable for elliptic curve cryptography, consisting of a private key d (a randomly selected integer in the interval
in the binary case) must be agreed upon. Also, each party must have a key pair suitable for elliptic curve cryptography, consisting of a private key d (a randomly selected integer in the interval 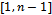 ) and a public key Q (where
) and a public key Q (where 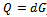 ). Let Alice's key pair be
). Let Alice's key pair be 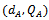 and Bob's key pair be
and Bob's key pair be 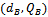 . Each party must have the other party's public key (an exchange must occur).Alice computes
. Each party must have the other party's public key (an exchange must occur).Alice computes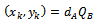 Bob computes
Bob computes 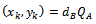 The shared key is
The shared key is 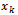 (the x coordinate of the point). The number calculated by both parties is equal, because
(the x coordinate of the point). The number calculated by both parties is equal, because 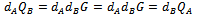 The protocol is secure because nothing is disclosed (except for the public keys, which are not secret), and no party can derive the private key of the other unless it can solve the Elliptic Curve discrete logarithm Problem.
The protocol is secure because nothing is disclosed (except for the public keys, which are not secret), and no party can derive the private key of the other unless it can solve the Elliptic Curve discrete logarithm Problem.4.4. Message Transmission
- It is not hard to modify the Elliptic Curve Diffie-Hellman key agreement protocol for the purpose of message transmission by using the ElGamal encryption method. Suppose that the set of message unit has been imbedded in E in some agreed upon way and Bob wants to send Alice a message
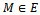 . Using the above method to exchange keys,
. Using the above method to exchange keys, 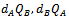 have already been exchanged. Bob now chooses another secret random integer, call this l, and sends Alice the pair of points
have already been exchanged. Bob now chooses another secret random integer, call this l, and sends Alice the pair of points 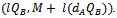 This is the encryption method, to decrypt this message Alice multiplies the first point in the pair by her secret key
This is the encryption method, to decrypt this message Alice multiplies the first point in the pair by her secret key 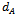 and then subtracts the result from the second point in the pair.
and then subtracts the result from the second point in the pair.4.5. The Elliptic Curve Discrete Logarithm Problem
- Referring to Definition 3.4.2 the discrete logarithm problem is the problem of computing from
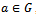 , a number s such that
, a number s such that 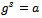 with respect to g provided that such an integer exists. This in the case of
with respect to g provided that such an integer exists. This in the case of 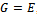 , the elliptic curve discrete logarithm problem to the base
, the elliptic curve discrete logarithm problem to the base 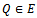 is the problem. Given
is the problem. Given 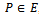 , of finding an integer x such that
, of finding an integer x such that 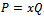 , if such x exists. The belief is that in practice it takes about the same amount of time to factor a well-chosen finite field as the factorization of an integer of approximately the same size. However, as in the case of factorization of an integer, there are many subexponential time algorithms to factor a well-chosen finite field. In the case of elliptic curves (except for supersingular ones,) the only methods available for finding discrete logs on
, if such x exists. The belief is that in practice it takes about the same amount of time to factor a well-chosen finite field as the factorization of an integer of approximately the same size. However, as in the case of factorization of an integer, there are many subexponential time algorithms to factor a well-chosen finite field. In the case of elliptic curves (except for supersingular ones,) the only methods available for finding discrete logs on 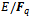 are the methods that apply to arbitrary groups. All of the algorithms have running time of the form
are the methods that apply to arbitrary groups. All of the algorithms have running time of the form 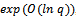 , provided that E is divisible by a large prime (a prime with an order of magnitude not much less than q)That is:Let E be elliptic curve over finite field
, provided that E is divisible by a large prime (a prime with an order of magnitude not much less than q)That is:Let E be elliptic curve over finite field 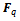 1) Take point
1) Take point 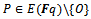 and compute
and compute 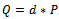 2) Elliptic Curve Discrete Logarithm Problem: given P and Q, compute dMuch work has been put into the solutions of both the DLP and the ECDLP. There are different attempts at solving both, but none have been conclusively shown to solve all cases of these problems. It is a field of mathematics with extensive work being covered[7]. Recently, technology-based attacks against smart cards raised concerns about the general security of this method[20]. One aspect of the elliptic curve encryption that revived the interest in it is that elliptic curve based cryptography is suitable for implementation on a quantum computer[21].
2) Elliptic Curve Discrete Logarithm Problem: given P and Q, compute dMuch work has been put into the solutions of both the DLP and the ECDLP. There are different attempts at solving both, but none have been conclusively shown to solve all cases of these problems. It is a field of mathematics with extensive work being covered[7]. Recently, technology-based attacks against smart cards raised concerns about the general security of this method[20]. One aspect of the elliptic curve encryption that revived the interest in it is that elliptic curve based cryptography is suitable for implementation on a quantum computer[21].5. The ElGamal Encryption Method
- The ElGamal encryption method[14] is closely connected to the Diffie Hellman key exchange protocol because the users can exchange a private key over an unsecured channel and then use this key to encrypt a message and send to the other. The security of this cryptosystem is based solely on the difficulty of solving the Diffie-Hellman problem[6].
5.1. Encrypting a Message Using the ElGamal Encryption Method
- The plaintext space is the set
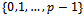 . To encrypt a plaintext m, Bob gets the authentic public key
. To encrypt a plaintext m, Bob gets the authentic public key 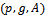 of Alice. He chooses a random integer
of Alice. He chooses a random integer 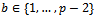 and computes:
and computes: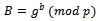 The number B is Bob’s key part from the Diffie-Hellman system. Bob determines:
The number B is Bob’s key part from the Diffie-Hellman system. Bob determines: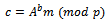 In other words, Bob encrypts the message m by multiplying it by the Diffie-Hellman key. The complete ElGamal ciphertext is the pair
In other words, Bob encrypts the message m by multiplying it by the Diffie-Hellman key. The complete ElGamal ciphertext is the pair 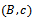 .
.5.2. Decrypting a Message using the ElGamal Encryption Method
- Alice has obtained the ciphertext
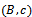 . She knows her secret key a. To obtain the plaintext m, she divides c by the Diffie-Hellman key
. She knows her secret key a. To obtain the plaintext m, she divides c by the Diffie-Hellman key 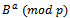 . In order to avoid inversions
. In order to avoid inversions 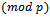 , she determines the exponent
, she determines the exponent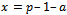 . Since
. Since 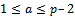 . We have
. We have 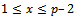 . Then she computes
. Then she computes 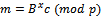 . That is, in fact, the original plaintext, as the following computation shows:
. That is, in fact, the original plaintext, as the following computation shows: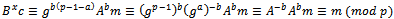 Example 3.5.1: Show how a use can encrypt a message and send it over an unsecured channel using the ElGamal encryption method.Solution: Alice chooses
Example 3.5.1: Show how a use can encrypt a message and send it over an unsecured channel using the ElGamal encryption method.Solution: Alice chooses 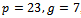 , and
, and 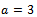 and computes
and computes  . Her public key is
. Her public key is 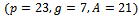 . Her secret key is
. Her secret key is 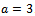 . Bob encrypts
. Bob encrypts 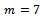 . He chooses
. He chooses 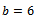 and computes
and computes  and
and 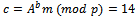 . The ciphertext is
. The ciphertext is 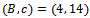 . Alice recovers m by computing
. Alice recovers m by computing 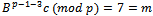 .Example 3.5.2: Show how a use can encrypt a message and send it over an unsecured channel using the ElGamal encryption methodSolution: As in Example 3.5.1, the public key of Alice is
.Example 3.5.2: Show how a use can encrypt a message and send it over an unsecured channel using the ElGamal encryption methodSolution: As in Example 3.5.1, the public key of Alice is 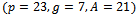 . Her secret key is
. Her secret key is 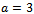 . As a precomputation, Bob chooses
. As a precomputation, Bob chooses 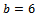 and computes
and computes 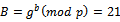 and
and  . Then he simply computes
. Then he simply computes 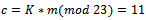 . The cipher text is
. The cipher text is 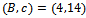 . Again Alice recovers the plaintext by computing
. Again Alice recovers the plaintext by computing 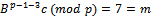 .The ciphertext is twice as long as the plaintext. This is called message expansion and is a disadvantage of this cryptosystem. On the other hand, the ElGamal system is a randomized cryptosystem, which can be regarded as an advantage.
.The ciphertext is twice as long as the plaintext. This is called message expansion and is a disadvantage of this cryptosystem. On the other hand, the ElGamal system is a randomized cryptosystem, which can be regarded as an advantage.6. The Knapsack Approach
- In this section the idea of cryptosystems based on the knapsack problem will be discussed. It was introduced by Merkle and Hellman in 1978[15]. The knapsack problem is a very interesting problem found in combinatorial optimization. It has various uses from the perspective of computer science. Studies have been done into the pseudo-polynomial time algorithm using dynamic programming, fully polynomial-time approximation scheme and of course in public key cryptosystems. This section will begin with a comprehensive introduction to the problem itself, and then a discussion of attempts at public key systems using this approach.
6.1. The Knapsack Problem
- Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to the given limit and the total value is as large as possible. In other words, you are given a set of positive integers
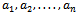 and an integer S, the knapsack problem asks which of these integers, if any, add together to give S. That is, consider the set of values
and an integer S, the knapsack problem asks which of these integers, if any, add together to give S. That is, consider the set of values 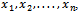 each either 0 or 1, such that:
each either 0 or 1, such that: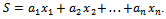 Considering the following example will give a better idea of how this works.Example 6.1.1: Show all the subsets of the set
Considering the following example will give a better idea of how this works.Example 6.1.1: Show all the subsets of the set 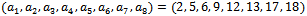 that add up to
that add up to 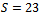 .Solution: By inspection we can see that there are four subsets that add up to 23. They can be seen as:
.Solution: By inspection we can see that there are four subsets that add up to 23. They can be seen as: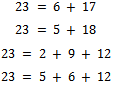 Equivalently, there are exactly four solutions to the equation
Equivalently, there are exactly four solutions to the equation 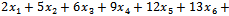
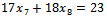 with
with 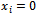 or 1 for
or 1 for 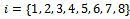 . These solutions are:
. These solutions are: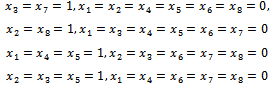 We can see that to verify that the equation
We can see that to verify that the equation 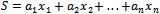 holds when
holds when 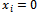 or 1 it takes at most n additions, which is much less then to search for solutions by trial and error which could take up to
or 1 it takes at most n additions, which is much less then to search for solutions by trial and error which could take up to 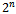 attempts. Definition 6.1.1: If a sequence of integers
attempts. Definition 6.1.1: If a sequence of integers 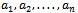 is such that the sum of the first
is such that the sum of the first 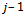 of these integers is always less than the jth integer, that is:
of these integers is always less than the jth integer, that is: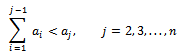 This sequence is called super-increasing.Example 6.1.2: Is the sequence
This sequence is called super-increasing.Example 6.1.2: Is the sequence 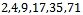 super-increasing?Solution: We can see that:
super-increasing?Solution: We can see that: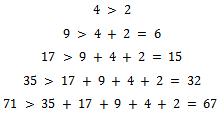 Thus, this sequence is super-increasing, as we wanted to show.Working with super-increasing sequences makes the knapsack problem much easier to solve, considering the following example will show this.Example 6.1.3: Is it possible to get a sum of 48, using the above super-increasing sequence:
Thus, this sequence is super-increasing, as we wanted to show.Working with super-increasing sequences makes the knapsack problem much easier to solve, considering the following example will show this.Example 6.1.3: Is it possible to get a sum of 48, using the above super-increasing sequence: 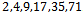 . Solution: Notice that we have
. Solution: Notice that we have 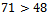 , so we cannot include 71 in any of our sums. Also notice that the elements which are less than 35, have a sum less than 35 when all added together:
, so we cannot include 71 in any of our sums. Also notice that the elements which are less than 35, have a sum less than 35 when all added together: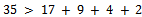 Thus 35 must be used in our sum; we can notice that we now have:
Thus 35 must be used in our sum; we can notice that we now have: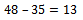 Again
Again 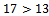 , which means it cannot be in our sum, we can easily notice among the final three integers that if we choose
, which means it cannot be in our sum, we can easily notice among the final three integers that if we choose 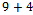 , we get the required sum. That is:
, we get the required sum. That is: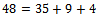 This is what we wanted to show.It can be noticed that in general to solve the knapsack problem of a super-increasing sequence
This is what we wanted to show.It can be noticed that in general to solve the knapsack problem of a super-increasing sequence 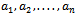 , that is to find the values of
, that is to find the values of 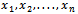 with
with 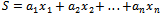 and
and 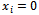 or 1 for
or 1 for 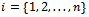 when S is given, we use the following algorithm. First we find
when S is given, we use the following algorithm. First we find 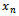 by noting that:
by noting that: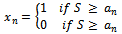 Then we find
Then we find 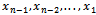 , in succession, using the equations
, in succession, using the equations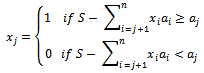 for
for 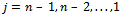 .Using this algorithm, knapsack problems based on super increasing sequences can be solved extremely quickly. The next section will discuss a cryptosystems based on this observation.
.Using this algorithm, knapsack problems based on super increasing sequences can be solved extremely quickly. The next section will discuss a cryptosystems based on this observation.6.2. Cryptosystems based on the Knapsack Problem
- The idea of using the knapsack problem as a cryptosystem was first thought up by Merkle and Hellman, and we initially considered a good choice for a public key cryptosystem. This idea has since then been broken[16], and the knapsack approach is now considered to be an infeasible method. The ciphers we will discuss in this section will be based on transformed super-increasing sequences. To be specific, let
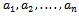 be super-increasing and let m be a positive integer with
be super-increasing and let m be a positive integer with 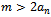 . Let w be an integer relatively prime to m with inverse
. Let w be an integer relatively prime to m with inverse 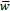 modulo m. We can now form the sequence
modulo m. We can now form the sequence 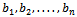 where
where 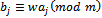 and
and 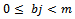 . We cannot use this special technique to solve a knapsack problem of the type
. We cannot use this special technique to solve a knapsack problem of the type 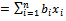 , where S is a positive integer, because the sequence
, where S is a positive integer, because the sequence 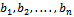 is not super-increasing in general. However, when
is not super-increasing in general. However, when 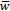 is known, we can find:
is known, we can find: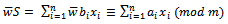 Because
Because 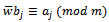 we see that:
we see that: 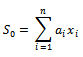 Where
Where 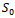 is the least positive reside of
is the least positive reside of 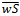 modulo m. We can easily solve the equation because
modulo m. We can easily solve the equation because 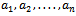 is super-increasing. This solves the knapsack problem:
is super-increasing. This solves the knapsack problem: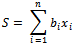 Because
Because 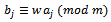 and
and 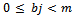 . This procedure can be shown with an example.Example 6.2.1: Use the above method to show the super-increasing sequence
. This procedure can be shown with an example.Example 6.2.1: Use the above method to show the super-increasing sequence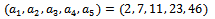 can be transformed using
can be transformed using 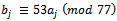 for
for 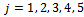 . When
. When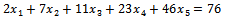 Solution: We can form the sequence
Solution: We can form the sequence 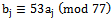 for
for 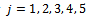 . That is
. That is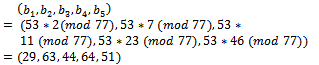 That is,
That is, 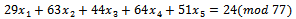 We can check to see if this transformation was successful by solving the original sequence, which is
We can check to see if this transformation was successful by solving the original sequence, which is 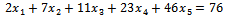 This sequence is super increasing which means we can follow the above procedure in Example 6.1.3.
This sequence is super increasing which means we can follow the above procedure in Example 6.1.3. 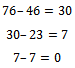 Thus, we have a solution of
Thus, we have a solution of 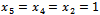 and
and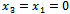 . We can check this solution with our above transformed sequence
. We can check this solution with our above transformed sequence 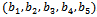 . We have
. We have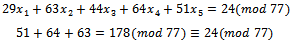 Which is what we wanted to show, thus our transformation was successful in making a super-increasing sequence into a sequence that is not super-increasing.The cryptosystem based on the knapsack problem invented by Merkle and Hellman works as follows:Each individual chooses a super-increasing sequence of positive integers of a specified length, say, N (for example,
Which is what we wanted to show, thus our transformation was successful in making a super-increasing sequence into a sequence that is not super-increasing.The cryptosystem based on the knapsack problem invented by Merkle and Hellman works as follows:Each individual chooses a super-increasing sequence of positive integers of a specified length, say, N (for example, 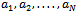 ) as well as a modulus m with
) as well as a modulus m with 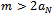 and a multiplier w with
and a multiplier w with 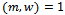 . The transformed sequence
. The transformed sequence 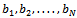 is made public.To send a message P to an individual, the message is first translated into a string of zeros and ones using the binary equivalents of letters given in Table 6.2.1 below. This string of zeros and ones is split into segments of length N; if N does not divide the length, simply fill out the last block with ones.For each of the blocks we have, a sum is computed using the sequence
is made public.To send a message P to an individual, the message is first translated into a string of zeros and ones using the binary equivalents of letters given in Table 6.2.1 below. This string of zeros and ones is split into segments of length N; if N does not divide the length, simply fill out the last block with ones.For each of the blocks we have, a sum is computed using the sequence 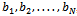 , for example, when we have the block
, for example, when we have the block 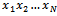 :
: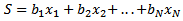 The sum generated by each block form a ciphertext message. Since
The sum generated by each block form a ciphertext message. Since 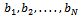 is not a super-increasing sequence, it is much harder to solve the knapsack cipher, without knowledge of m and w. When someone knows m and w, the knapsack problem can be transformed into a super-increasing sequence, which makes for a much easier knapsack problem. For someone with knowledge of m and w, we get:
is not a super-increasing sequence, it is much harder to solve the knapsack cipher, without knowledge of m and w. When someone knows m and w, the knapsack problem can be transformed into a super-increasing sequence, which makes for a much easier knapsack problem. For someone with knowledge of m and w, we get: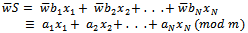 where
where 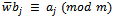 , where
, where 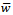 is an inverse of w modulo m, so that:
is an inverse of w modulo m, so that: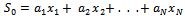
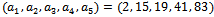 . Let our
. Let our  , so that
, so that 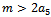 , and
, and 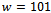 , thus we can see that we have
, thus we can see that we have 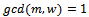 . Encrypt the message KNAPSACK and show the decryption process.Solution: We begin by transforming our super-increasing sequence
. Encrypt the message KNAPSACK and show the decryption process.Solution: We begin by transforming our super-increasing sequence 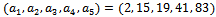 into a sequence that is not super-increasing, we note:
into a sequence that is not super-increasing, we note: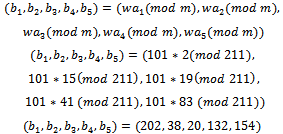 To translate this message, we must first translate the letters of the message into their five-digit binary equivalents and put them into blocks of length N, this sequence is of length 5, so the blocks will also be of length 5.We now have:01010 01101 00000 01111 10010 00000 00010 01010For each block of 5 binary digits, we form a sum by adding together the appropriate terms of the sequence in the slots corresponding to the positions of the block containing a digit equal to 1. This gives us:170 212 0 344 334 0 132 170This string of 8 sums is our found ciphertext. We can see that this example is very simplistic, although the decrypted message is protected from basic attacks.To decrypt and arrive back at our original message we must find the least positive residue modulo 211 of 117 times each sum. We can calculate the inverse of 101 modulo 211 to be 117. Once we finish this we can solve the corresponding easy knapsack problem with respect to the original super-increasing sequence
To translate this message, we must first translate the letters of the message into their five-digit binary equivalents and put them into blocks of length N, this sequence is of length 5, so the blocks will also be of length 5.We now have:01010 01101 00000 01111 10010 00000 00010 01010For each block of 5 binary digits, we form a sum by adding together the appropriate terms of the sequence in the slots corresponding to the positions of the block containing a digit equal to 1. This gives us:170 212 0 344 334 0 132 170This string of 8 sums is our found ciphertext. We can see that this example is very simplistic, although the decrypted message is protected from basic attacks.To decrypt and arrive back at our original message we must find the least positive residue modulo 211 of 117 times each sum. We can calculate the inverse of 101 modulo 211 to be 117. Once we finish this we can solve the corresponding easy knapsack problem with respect to the original super-increasing sequence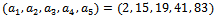 We then have:
We then have: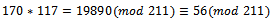 We can see that
We can see that 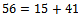 , which corresponds to the binary representation of 01010.
, which corresponds to the binary representation of 01010.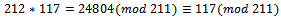 We can see that
We can see that 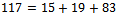 , which corresponds to the binary representation of 01101.
, which corresponds to the binary representation of 01101.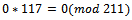 We can see that we have a corresponding representation of 00000.
We can see that we have a corresponding representation of 00000.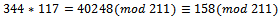 We can see that
We can see that 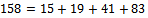 , which corresponds to the binary representation of 01111.
, which corresponds to the binary representation of 01111.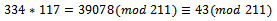 We can see that
We can see that 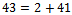 , which corresponds to the binary representation of 10010.
, which corresponds to the binary representation of 10010.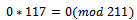 We can see that we have a corresponding representation of 00000.
We can see that we have a corresponding representation of 00000.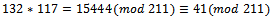 We can see that
We can see that 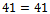 , which corresponds to the binary representation of 00010.
, which corresponds to the binary representation of 00010.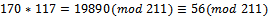 We can see that
We can see that 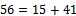 , which corresponds to the binary representation of 01010.Thus our decrypted message comes out to be:01010 01101 00000 01111 1001000000 00010 01010K N A P SA C KThis is our original message and we have properly encrypted and decrypted the message.Knapsack ciphers were originally thought to be excellent candidates as an alternate form of public key encryption instead of the standard RSA approach. However, in 1982 Shamir (one of the inventors of RSA) showed they do not provide satisfactory security for encryption of messages. The reason being, he had found an efficient algorithm for solving knapsack problems involving sequence
, which corresponds to the binary representation of 01010.Thus our decrypted message comes out to be:01010 01101 00000 01111 1001000000 00010 01010K N A P SA C KThis is our original message and we have properly encrypted and decrypted the message.Knapsack ciphers were originally thought to be excellent candidates as an alternate form of public key encryption instead of the standard RSA approach. However, in 1982 Shamir (one of the inventors of RSA) showed they do not provide satisfactory security for encryption of messages. The reason being, he had found an efficient algorithm for solving knapsack problems involving sequence 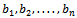 with
with 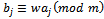 where m and w are relatively prime positive integers and
where m and w are relatively prime positive integers and 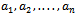 is a super-increasing sequence. This is why knapsack ciphers are not used in modern day cryptography.
is a super-increasing sequence. This is why knapsack ciphers are not used in modern day cryptography.7. Conclusions
- In this paper we have described and compared five of the major public key cryptosystems developed in the last forty years. Although they all share some characteristics, they are based on a variety of hard mathematical problems: the factorization of a number into primes, the one way trapdoor functions, the elliptic curve arithmetic, and the discrete logarithms in finite fields. As the researchers develop cryptosystems, they have to argue that they are hard to break and therefore useful. At the same time they have to study the ways to break them, serving as further reassurance of the strength of the cryptosystems. The importance of the public key cryptosystems lies in their accessibility, and thus their practicality.Most authors consider the RSA systems to be the most secure. It is well studied and implemented and widely used. It is widely believed that even if the factorization problem is solvable in polynomial time, which is currently not known, increasing the size of the primes used in the key generation will keep the method secure for years to come. The Diffie-Hellmann key exchange and the ElGamal encryption method based on it are a very useful in understanding the basics of exponentiation based cryptography. It is further important for the study of the strengths and weaknesses of any cryptosystem based on exponentiation, and thus valuable cryptanalytic tool. The discrete logarithm problem became one of the most studied problems due to this.Elliptic curve based cryptography has one very important feature that appeals to the manufacturers of security protected electronic equipment – quicker calculations compared to the other major cryptographic algorithms. However, both theoretically and from the point of view of its hardware implementation it is less secure than RSA. Another appealing feature of the elliptic curve cryptography is its applicability under the quantum computing paradigm, which spurs further research into this approach. The knapsack approach had important role in the development of the idea of a cryptosystem based on one way trapdoor function. Today, we know that the knapsack cipher is not secure enough for practical applications, due to its polynomial time breakability.
ACKNOWLEDGEMENTS
- Dr. Vassilev’s research is supported by NSERC Discovery Grant. Andrew Twizell would like to acknowledge the help and support of Dr. Vassilev during the work on this paper.
References
| [1] | Neal Koblitz. Algebraic Aspects of Cryptography. Berlin, Springer, 1999. |
| [2] | Johannes A. Buchmann. Introduction to Cryptography. Springer, New York, 2004. |
| [3] | Joseph A. Gallian. Contemporary Abstract Algebra. Brooks/Cole, Australia, 2010. |
| [4] | John Stillwell. Elements of Number Theory. Springer, New York, 2003. |
| [5] | Kenneth H. Rosen. Elementary Number Theory and Its Applications. Pearson/Addison Wesley, Boston, 2011. |
| [6] | Ueli M. Maurer and Stefan Wolf. The Diffie-Hellman Protocol. Designs, Codes and Cryptography 19: 147–171, 2000. |
| [7] | Neal Koblitz, Alfred Menezes and Scott Vanstone. The State of Elliptic Curve Cryptography. Designs, Codes and Cryptography 19: 173–193, 2000. |
| [8] | Christiane Rousseau and Yvan Saint-Aubin. Mathematics and Technology. Springer, New York, 2008. |
| [9] | Ronald Rivest, Adi Shamir and Leonard Adleman. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Communications of the ACM 21(2): 120–126, 1978. |
| [10] | Alfred Menezes, Paul C. van Oorschot and Scott A. Vanstone. Handbook of Applied Cryptography. CRC Press, 1996. |
| [11] | Dan Boneh. Twenty Years of attacks on the RSA Cryptosystem. Notices of the American Mathematical Society 46 (2): 203–213, 1999. |
| [12] | Withfield Diffie and Martin E. Hellman. New Directions in Cryptography. IEEE Transactions on Information Theory, vol. IT-22: 644–654, 1976. |
| [13] | Martin E. Hellman. An Overview of Public Key Cryptography. IEEE Communications Magazine, 42–49, 2002. |
| [14] | Taher ElGamal. A Public-Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. IEEE Transactions on Information Theory 31 (4): 469–472, 1985. |
| [15] | Ralph Merkle and Martin E. Hellman. Hiding information and signatures in trapdoor knapsacks. IEEE Transactions on Information Theory 24 (5): 525–530, 1978. |
| [16] | Adi Shamir. A polynomial-time algorithm for breaking the basic Merkle - Hellman cryptosystem. IEEE Transactions on Information Theory 30 (5): 699–704, 1984. |
| [17] | Neal Koblitz. Elliptic curve cryptosystems. Mathematics of Computation 48 (177): 203–209, 1987. |
| [18] | Victor S. Miller. Use of elliptic curves in cryptography. CRYPTO 85: 417–426, 1985. |
| [19] | Y. Hitchcock, E. Dawson, A. Clark and P. Montague. Implementing an efficient elliptic curve cryptosystem over GF(p) on a smart card. ANZIAM Journal 44, 2002. |
| [20] | Ingrid Biehl, Bernd Meyer and Volker Müller. Differential Fault Attacks on Elliptic Curve Cryptosystems. Advances in Cryptology – CRYPTO 2000. Lecture Notes in Computer Science 1880: 131–146, 2000. |
| [21] | Michael A.Nielsen and Isaac L.Chuang. Quantum Computation and Quantum Information. 2002 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML