1. Introduction: Systems Thinking

According to Monat and Gannon (2015a and b, 2017) Systems Thinking is a perspective, a language, and a set of tools. It focuses on relationships among system components (as opposed to the components themselves), it is holistic instead of analytic, it recognizes that systems are dynamic and usually include multiple feedback loops, and it acknowledges that systems often exhibit emergent and self-organizing behaviors. In those previous works, Monat and Gannon have shown how Systems Thinking can explain and address political and socio-economic issues. In this paper, we describe how Systems Thinking can explain a great many natural patterns in the world: why zebras have stripes, why geese fly in a V-formation, why fish school, why the universe looks as it does, and how life began on earth. The explanation begins with the Iceberg Model.

The Iceberg Model. Systems Thinking posits that repeated events or objects represent patterns and that those patterns are caused by systemic structure, which is (in turn) caused by underlying forces. The patterns are often emergent, meaning that they cannot be predicted from knowledge of the system components; only when those components interact do the patterns emerge. The underlying structures represent the interactions or relationships among system components: the system’s stocks, flows, and feedback loops. Structures develop because of natural underlying forces in natural systems or because of mental models in human-designed systems. The Iceberg Model conveniently shows the relationships among events, patterns, structures, and underlying forces (Figure 1).

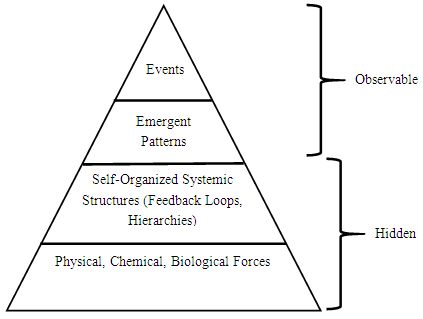Figure 1. The Iceberg Model for Natural Systems (after Monat and Gannon, 2015a)

For example, the underlying forces of gravity and centrifugal force result in the structure of the solar system, which in turn results in patterns of day and night on planets, the patterns of planetary orbits around the sun, and the patterns of seasons on earth. In a corporation, the underlying mental model that “money motivates employees” results in an incentive compensation structure which, in turn, results in a pattern of excellent performance in some employees. There may be unintended consequences of the structures, as well: an unsavory employee may attempt to take credit for work that she did not do in order to increase her own compensation.

To reiterate, natural patterns (often emergent) are caused by self-organized structures (feedback loops, hierarchies) and their underlying forces. Good systems thinkers try to first recognize and then explain patterns by attempting to understand the underlying structures and forces that yield the patterns. Each of these concepts is explained in greater detail in the following sections.

2. Patterns

Businessdictionary.com defines a pattern as a consistent and recurring characteristic or trait that helps in the identification of a phenomenon or problem, and serves as an indicator or model for predicting its future behavior. Patterns may be physical, temporal, behavioral, psychological, or some combination. Examples of physical patterns include stripes on zebras, crystals, sand dunes ripples, compound fly eyes, and termite cathedrals. Temporal patterns are exemplified by predator-prey populations over time, Newton’s cradle, my boss being grouchy every Thursday, and the spawning runs of salmon every autumn. Combination physical-temporal patterns include traffic jams, birds flocking, and fish schooling.

3. Emergence

Natural patterns are usually emergent—that is, they are properties of the system that cannot be predicted from the properties of the system’s components. These emergent properties develop as result of the relationships among the system elements or between the system elements and the environment. The V-formation of geese, for example, could not be predicted from the flying characteristics of a single goose. It is only when several geese fly together that the V-pattern emerges. Similarly, fish schooling would not be predicted form the swimming characteristics of a single fish. Camazine et al. (2001) say, “Emergence refers to a process by which a system of interacting subunits acquires qualitatively new properties that cannot be understood as the simple addition of their individual contributions.” Johnson (1999) says, “Emergence is what happens when an interconnected system of relatively simple elements self-organizes to form more intelligent, more adaptive higher-level behavior. It's a bottom-up model; rather than being engineered by a general or a master planner, emergence begins at the ground level. Systems that at first glance seem vastly different--ant colonies, human brains, cities, immune systems--all turn out to follow the rules of emergence. In each of these systems, agents residing on one scale start producing behavior that lies a scale above them: ants create colonies, urbanites create neighborhoods.” Emergent patterns are often a result of self-organized systemic structures such as feedback loops and hierarchies, which are in turn caused by underlying forces.

4. Structure

Systemic structure is the way that system elements are linked together and relate to each other, as well as to their environment. Meadows (2008) defines structure as the system’s interlocking stocks, flows, and feedback loops. Natural structures are self-organized and include the structure of atoms and solar systems, the physical structure of an animal or crystal, and the herds and flocks of grouped animals. Feedback loops, self-organization, and hierarchies are important elements of natural system structure.

Feedback Loops

Multiple feedback loops are present in most systems. As shown in Figure 2, these feedback loops may be positive/reinforcing (such as compound interest on a savings account) or negative/balancing (as a home thermostat or cruise control on an automobile.)

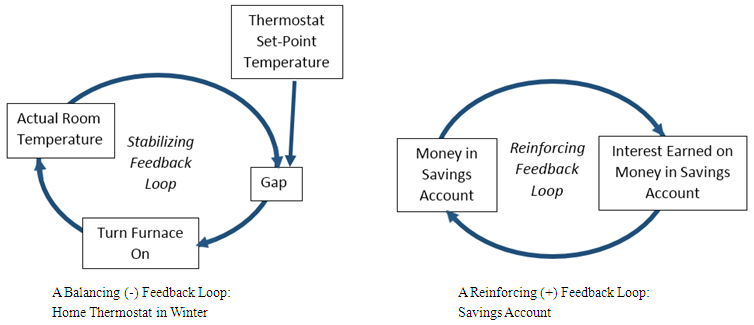Figure 2. Balancing and Reinforcing Feedback Loops

Feedback loops cause oscillations in several different ways. Stabilizing (balancing) Feedback Loops with delays cause oscillation because of the delays. (Delays arise from several sources: physical delays may exist due to inertia or momentum, physiological delays may exist because of finite gestation periods or reaction times, perceptual delays exist because of the time required for plants and animals to realize and react to situations.) Figure 3 shows a Behavior-Over-Time plot for a predator-prey system involving rabbits and foxes.

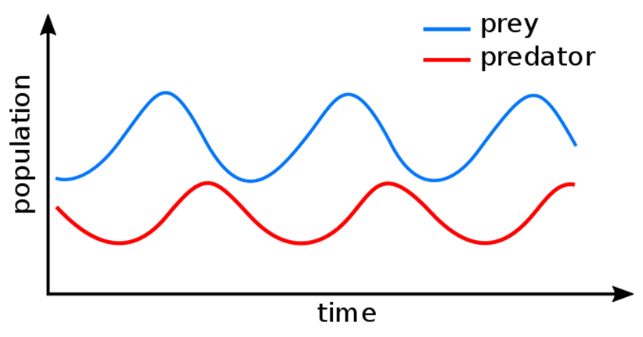Figure 3. Behavior-Over-Time Plot for Predator and Prey

Suppose that initially there is a population of rabbits living happily in a field at the edge of a woods. They mostly eat, sleep, and procreate. One day, a pair of foxes wander buy and decide to settle down because of the abundant cunicular food supply. The foxes prey on the rabbits and raise a healthy litter of fox kits, who, in turn, grow and raise their own families, all of which prey on the rabbits. Eventually, there are so many foxes that the population of rabbits starts to decline due to predation. Fewer rabbits means that fewer foxes can be supported, but the effect is not immediate: it may take months, or even years, for the fox population to decline in response to the declining rabbit population. This delay is because of the finite gestation period for both rabbits and foxes; the finite time required to hunt, kill, and digest a rabbit; and for the time required for the lack of food to affect the foxes’ decision to move on. Eventually, it does, the rabbit population starts to rebound, the foxes proliferate in response, and the cycle repeats. If there were no delays, the system would not oscillate, but instead would reach a steady-state value and stay there.

Figure 4’s behavior-over-time plot (which corresponds to the home thermostat causal loop diagram of Figure 2) shows another example of systemic physical delays causing oscillations in a domestic heating system.

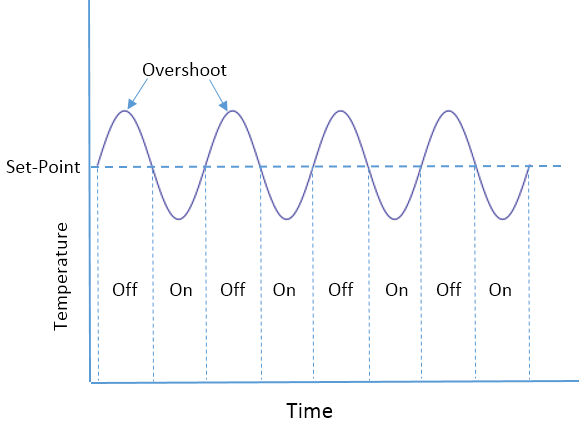Figure 4. Temperature Oscillation in a Domestic Heating System

When it is cold out and the outside temperature drops below a set-point, the thermostat causes the home’s furnace to start up. But heat transfer takes time, and because of the thermal mass of the house, the temperature response to increases in heat is not immediate. Furthermore, once the set-point temperature is reached and the furnace shuts down, the temperature continues to rise a little as residual heat in the system’s pipes and fluids is transferred to the home even though the burner is off; the result is an overshoot of the set-point temperature. This yields the sinusoidal temperature oscillation around the set-point depicted in Figure 4. Note that if there were no delays, the system temperature would approach its set-point smoothly and without oscillation.

Positive (reinforcing) feedback loops also cause oscillations when the reinforcing feedback loop is broken due to physical constraints. Examples include sand dune ripples and ocean waves for which gravity collapses the mounding piles of sand or water that are developed due to reinforcing feedback loops; and some cloud formations for which the cloud-forming reinforcing feedback loop is broken by turbulent mixing. (These patterns will be described more fully subsequently.)

So both stabilizing feedback loops with delays and reinforcing feedback loops with breaks cause oscillations. Those oscillations represent patterns. (Note that system dynamic software such as isee’s Stella Architect and Ventana System’s VenSim may be used to develop dynamic models that show the oscillatory behavior.) The natural feedback loops often develop because of self-organization.

Self-Organization

Natural systems tend to self-organize into structures due to underlying forces. Packs of wolves develop an organizational hierarchy. Ants organize into marching columns. Wildebeests organize into herds. Even inanimate systems self-organize. As a super-saturated salt solution cools, Na and Cl atoms organize into a precisely-arranged crystal. Groups of stars organize into spiral or globular clusters. DNA components self-assemble into DNA molecules, then disassemble and replicate. Camazine (2001) says, “Self-organization is a process in which a pattern at the global level of a system emerges solely from numerous interactions among the lower-level components of the system. Moreover, the rules specifying interactions among the system's components are executed using only local information, without reference to the global pattern.” According to Beckenkamp (2006), “Self-organization exists if – independent of the intentions or even existence of an organizer or a central plan – regular or arranged patterns emerge from the interactions in the system itself.” Self-organizing activities do not happen by chance, but instead due to specific underlying forces. Natural hierarchies are a common structure resulting from self-organization.

Hierarchies

Many complex natural systems are hierarchical—that is, they comprise sub-systems which, in turn, comprise sub-systems of their own, etc., until the most fundamental sub-system comprises the raw system elements. (Systems Engineers would call this concept “System of Systems” or “SoS.”) Examples include the universe (galactic clusters, galaxies, solar systems, planets with moons); the human body (the human organism; the circulatory, reproductive, digestive, and other systems; the blood vessels and organs; the organ sub-structures; the individual cells); ecosystems (plants and animals, trees, tree components such as leaves, leaf sub-structures such as veins and epidermis, cells, cell components,) and many load-bearing biological tissues such as wood and bone (Fratzl and Weinkamer, 2007.) Natural hierarchies persist because of benefits to both the lower levels and upper levels in the structure: each sub-unit benefits from the organization, protection, and support of the higher level; and the higher level benefits from the added functionality and quantity of the sub-unit. Hierarchies thus represent symbiotic relationships between sub-units and their superiors, in a chain of reinforcing feedback loops that permeates the entire system.

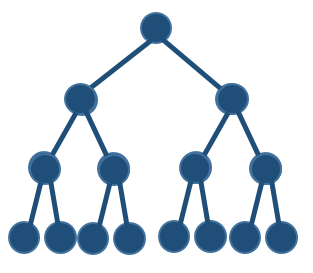Figure 5. Hierarchical Pattern

Hierarchies themselves are often patterns (Figure 5). For example, the unit of a mass orbiting around a larger, central mass is repeated at several different scales in the universe. But it may be hard to see the hierarchical structure in complex systems. Recognizing the hierarchical structure and then understanding how that structure evolved over time helps understand how the system came to be.

To help with this, one must understand that self-organizing hierarchies evolve from the bottom up: multi-cell organisms from single-cell; complex protein configurations from simpler ones; a complex human brain from a primitive collection of ganglia. The underlying forces driving this self-organization may be chemical, physical, electrical, or other; but the newly self-organized structure typically has a competitive advantage, which leads to its evolutionary persistence. An example is the evolution of herding behavior in wildebeests. Individual wildebeests were easy picking for predators. By chance or by some natural affinity, several wildebeests grouped together and were safer from predators. In subsequent generations, those wildebeests that displayed this herding tendency survived better than singular animals, so the tendency to herd was passed down. Thus a hierarchy was formed: individual wildebeests into groups; groups into herds. The reinforcing feedback loop in this situation is clear: individual wildebeests with superior survival traits survive better than those who don’t and therefore more of them pass down their genes. Their progeny survive better and, in turn, more of them pass down their genes, etc. Eventually, those wildebeests with better survival traits or “fitness” predominate and those with poorer fitness die out. This is the basis for natural selection and evolution.

Meadows (2008) advances another reason for the prevalence and stability of natural hierarchies. She states that “Complex systems can evolve from simple systems only if there are stable intermediate forms. The resulting complex forms will naturally be hierarchic. That may explain why hierarchies are so common in the systems nature presents to us. Among all possible complex forms, hierarchies are the only ones that have had time to evolve.”

The modern prokaryotic plant cell is a good example of natural hierarchies facilitating the evolution of complex systems. Modern plant cells can efficiently photosynthesize and transfer energy, but this was not the case for their primitive ancestors. It is believed that modern plant cells evolved from primitive eukaryotes by engulfing specialized independent bacteria such as aerobic prokaryotes (which evolved into mitochondria, the cell’s energy-transfer organelle) and photosynthetic prokaryotes (which evolved into chloroplasts, the cell’s photosynthetic organelle) to become complex photosynthetic eukaryotes; viz. modern plant cells (Scitable, 2017.) This process (termed endosymbiosis) was itself a feedback loop: the parent cell benefits from the energy production and photosynthesis of the mitochondria and chloroplasts; and they in turn benefit from the protection and nutrients of the parent cell. This evolution would have taken much longer, and perhaps not have happened at all, were it not for the availability of the 3 primitive sub-units: the primitive eukaryote, the aerobic bacterium, and the photosynthetic bacterium, all lower levels on the hierarchy.

Much natural self-organization into hierarchies works similarly. It is much easier to understand the structures of DNA, complex life forms, and the universe if one understands that the end result evolved from simpler sub-systems that were themselves more structured than their raw components. The hierarchical organization of many natural structures contributes to the patterns we see while explaining how complex systems evolved.

5. Underlying Forces (Mechanisms of Self-Organization)

In natural systems, there are many underlying forces yielding self-organization:

Ÿ Physical mechanisms such as gravity, electromagnetic force, the strong and weak nuclear forces, aerodynamic lift, fluid shear, friction, pressure, mechanical forces, centrifugal force

Ÿ Chemical mechanisms such as pheromones, the electronic charge of ions, Vander Walls forces, hydrophilicity/hydrophobicity, chemical potential, the physical shape and structure of molecules

Ÿ Instinctive survival mechanisms such as swarming, flocking, schooling, herding to afford a competitive advantage

Ÿ Comfort/Discomfort perceptions such as safety zones, sensitivity to heterogeneity, separation, alignment, and cohesion

In human-designed systems, the underlying forces are typically mental models such as “incentive compensation increases productivity,” “honesty is the best policy,” and “competition brings out the best in people.” Several examples of patterns, their underlying structures, and the structures’ causative underlying forces are presented in Table 1.

Table 1. Some Examples of Patterns, their Causative Structures, and their Underlying Forces

6. Patterns in Nature

There are hundreds of patterns occurring naturally. Although some of these seem beyond understanding, systems thinking may be used to explain each of them.

Sand Dune Ripples. The intricate ripples in sand dunes (Figure 6) are explainable using Systems Thinking. As wind moves along a flat bed of sand, it may happen to dislodge a single sand grain, carry it along for a bit, and then deposit it on top of the flat sand surface. This obstacle causes the horizontal wind to divert upwards. This upward wind direction then carries additional sand grains over the original grain and deposits them. The pile of sand is now a little bigger and causes the wind to bend upwards even more. As the process continues, more and more sand accumulates until the slope is so steep that a mini-avalanche of sand occurs due to gravity. Meanwhile, the shape of the newly-formed ripple causes the wind to detach from the surface, re-attach downstream, and repeat the process (Makse, 2017.)

In this situation, the feedback loop is physical: The result of the wind force (the sand ripple) impacts the wind force itself (the wind direction) which then impacts the shape of the ripple, which, in turn, impacts the direction of the wind in a reinforcing feedback loop that continues until gravity topples the top of the ripple. Wind accumulates; gravity topples. This is an example of a reinforcing feedback loop proceeding to failure (due to an interruption by gravity) and then starting up again.

Figure 6. Sand Dune Ripples

Crystals. Systems thinking may be used to explain crystal formation using sodium chloride (NaCl) as an example (Figure 7). In an aqueous solution, the positively charged sodium atoms Na⁺ and negatively charged chloride atoms Cl^- are fully dissociated as charged ions. If the solution cools, the attractive electrostatic forces will cause a Na⁺ and a Cl^- atom to join together to form a NaCl molecule, the sodium end of which has a + charge and the chloride end of which has a negative charge. Once this initial “seed” molecule forms, its electrostatic forces will attract other Na⁺ and Cl^- ions from the solution: Na⁺ will bind to Cl^- and vice versa. This will occur in 3 dimensions (Figure 8), meaning that the structure will grow in all directions, yielding a sold-state crystal which precipitates out of the solution. It will be highly ordered in that all Cl atoms will be surrounded by Na atoms, and all Na atoms will be surrounded by Cl- atoms, as shown in Figure 8. The feedback loop is evident: + attracts – and – attracts + in a reinforcing loop which causes the crystal to grow. The underlying forces are electrostatic attraction and repulsion. Growth will continue until free Na and Cl ions are no longer available.

Figure 7. Salt Crystals

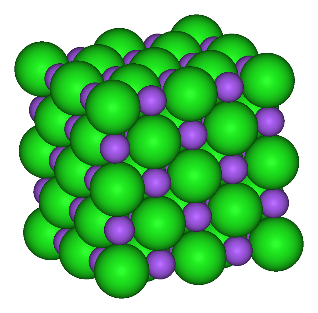Figure 8. NaCl Ion Pattern. The green spheres represent Cl- ions and the purple spheres represent Na+ ions

Newton’s Cradle. Newton’s cradle is a pendulum-like device in which multiple pendulum bobs transfer energy and swing in mesmerizing patterns (Figure 9). As for a simple pendulum, the magnitude of the restoring force (which is the tangential component of gravitational force) increases the farther the bob is displaced from its equilibrium position. But the bob position, in turn, is a function of the forces acting on it. Adding a few more bobs and efficient momentum transfer yields the Newton’s Cradle patterns. The feedback loop is shown in Figure 10.

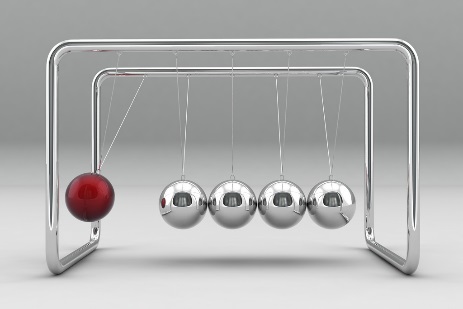Figure 9. Newton’s Cradle

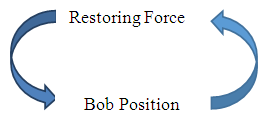Figure 10. Stabilizing Feedback Loop for Newton’s Cradle

The restoring force impacts the bob’s position and the bob’s position impacts the restoring force. Because the restoring force resists bob positions further from equilibrium (after all, it is a “restoring” force) this feedback loop is negative, or stabilizing.

Zebra Stripes. Scientists have studied the causes of zebra stripes (Figure 11) for a long time. Current thinking invokes a balancing feedback process involving an “activator” chemical that turns on the dark pigment melanin, and an “inhibitor” that suppresses the activator. These 2 chemicals impact each other in a negative feedback loop:

Figure 11. Zebra Stripes

Figure 12. Balancing Feedback Loop for Zebra Stripes

The result is a chemical oscillation yielding the stripes that we see. This phenomenon was modeled and described by Alan Turing (1952) who studied animal patterns and developed a “reaction-diffusion” mathematical model in which a rapidly diffusing inhibitor reacts with a slowly diffusing activator. The Turing Reaction-Diffusion model involves several adjustable variables that control diffusion and reaction rates. By adjusting these variables, scientists have been able to create a variety of animal coloration patterns (Howard Hughes Medical Institute, 2005.) The zebra stripes represent oscillations, which are caused by feedback loops.

Compound Eyes. Many insect eyes display beautiful patterns with hundreds of individual lenses laid out in geodesic-like hemispheres (see Figure 13). Myers (2006) says, “You might even say, if you found a fly eye upon a heath, that you could not imagine how something so beautiful and perfectly arranged and organized could possibly have come into existence without some superhuman engineering.” He explains this as follows: “This is easy to understand: the cells in the fly eye are doing The Wave. After the wave has passed, cells form small clusters and signal each other; one cell sets itself apart and begins to differentiate into the R8 cell, and recruits two neighbors to form the R2 and R5 cells. Subsequently, R3 and R4 are drawn in, then R1 and R6, and finally, R7. The cells all have the same orientation to one another. It's all quite mechanical and reliable, mediated by a small set of genes…… EGF-R signalling is activated by the ligand, Spitz, and inhibited by the secreted protein, Argos.” Without understanding the specific cell nomenclature and biomechanics, it is still clear that the ligand Spitz and the protein Argos are opposing forces that impact each other in a feedback loop. This is similar to the zebra stripe activator-inhibitor mechanism, but causing physical structure instead of pigmentation.

Figure 13. Fly Eyes

Geese V-Formations. If you had never seen geese in flight, even if you understood the lift generated by trailing vortices, you would never guess that when you put a flock of geese together, they will form a V (Figure 14). The pattern emerges because of the relationships among the components of the system. When an airfoil (such as a goose’s wing) moves through the air, a vortex trails off the airfoil’s tip. The vortex is a spiral of air rotating about a horizontal axis (see Figure 15) with one side of the vortex moving up and the other side moving down. The upward-moving side provides additional lift and makes it easier for another object to fly at that location. So a trailing goose naturally moves around behind a leading goose until it finds the greatest lift. The negative (or stabilizing) feedback loop in this case is the reduced lift as the goose flies further away from the center of the rising side of the vortex. Goose flies away from the uplift side of the vortexàless liftàgoose flies closer toward the uplift side of the vortexàmore lift. The results when several geese fly together is the iconic V. The oscillation in this case is more subtle. It occurs because a single goose following a preceding goose’s trailing vortex becomes the leader for a following goose. Thus every goose (except the lead and last geese in a gaggle) is both a cause and effect, as shown in Figure 16.

Figure 14. Geese in V-Formation

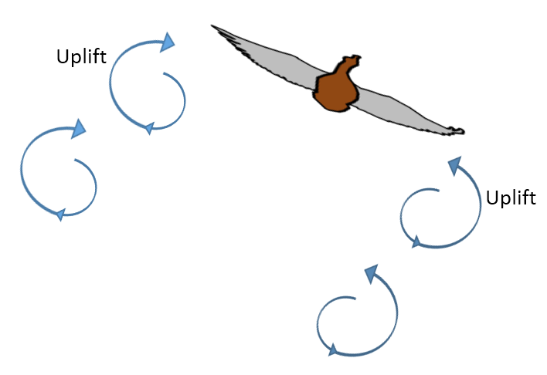Figure 15. Trailing Vortices

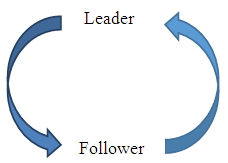Figure 16. Reinforcing Feedback Loop for Geese

The V-formation may be interpreted as a broken (but still functional!) reinforcing feedback loop. Imagine a gaggle of geese flying in a circle, one behind the other and offset, each taking advantage of its predecessor’s trailing vortex (Figure 17). This would be a very efficient flight structure with the only disadvantage being that the geese would not fly anywhere. If the circle is broken, one obtains the classic V-formation. Deneubourg (1989, 1990) has studied and written extensively on pattern formation in social animals such as ruminant herds and fish.

Figure 17. Geese Flying in a Circle

Fish Schools. Fish schooling (Figure 18) may be explained using systems thinking at 2 different scales, both of which are evolutionary and related to survival. At the macro level, there is safety in numbers; being with a group of your species reduces the likelihood that an individual will be preyed upon. Schooling was reinforced as a greater number of fish who tended to school together survived to pass their genes on to subsequent generations, while those who did not school died off as they were preyed upon. The reinforcing feedback loop strengthened the schooling tendency in every new generation. At the micro level, the fish follow the 3 rules of group behavior: maintain the general speed of your neighbors, maintain the general direction of your neighbors, and don’t get too close to your neighbors. Note that these rules form several counteracting feedback loops: if I go too slow, speed up; if I steer too far left, correct by steering right, and if I get too close, move farther away. But the dominant feedback loop, which applies to many animal group movements, is depicted in Figure 19: The position and motion of the group impacts the position and motion of each individual which, in turn, collectively impacts the position and motion of the group.

Figure 18. Fish School

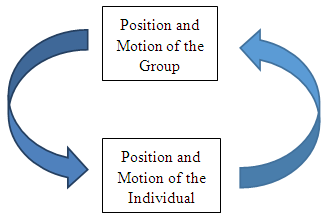Figure 19. The Dominant Feedback Loop Describing Group Motion

The result is that the fish school appears to oscillate or undulate as it moves through the water (Muhammad Saif Ullah et al., 2016; Miller et al., 2017.)

Herd Patterns. Herding behavior describes the tendency of groups of animals to move together in a pattern. It is observed in wolves, deer, sheep, goats, horses, bison, cattle, wildebeests, caribou, elephants, and many other species. The behavior often looks organized as depicted in Figure 20. This structure derives from 2 instincts: 1) it is safer to stick with a group than to be out alone, 2) avoid getting trampled. Similar to fish schooling, these instincts likely evolved as survival mechanisms—those who happened to follow these “rules” survived better than those who did not, and were thus able to pass on their genes to their offspring so that these instincts were perpetuated and strengthened in subsequent generations. The instincts resulted in 3 behavioral “rules:” 1) follow the general direction of your neighbors, 2) maintain the general speed of your neighbors, and 3) don’t get too close to your neighbors. Note the feedback loops established by these rules, which yield the familiar undulating herd patterns exemplified in Figure 20 deriving from the generic feedback loop shown in Figure 19. It is interesting to note that these stabilizing feedback loops may yield relaxed, slow movement or stampedes, and anything in between. Unlike for birds or fish, the oscillatory nature of land animal group behavior is limited to 2 dimensions.

Figure 20. Arctic Caribou Herd

Bird Murmuration. Bird murmuration is a spectacular natural phenomenon, characterized as a shape-shifting cloud of thousands of birds whose movements appear coordinated (Figure 21). As for schooling and herding animals, the natural forces underlying murmuration are instinctive, resulting in 3 familiar “group movement” rules: 1) alignment: follow the general direction of your flockmates, 2) cohesion: steer toward the average position of your flockmates, and 3) separation: maintain a “comfort zone”-- don’t get too close to your flockmates (Reynolds, 1987 and 2017.) Adding a little randomness caused by wind or distractions yields the mesmerizing aerial clouds that sometimes appear to be a single living, moving creature. The simple instinctive rules (mental models) yield balancing feedback loops at the micro scale (e.g. “I am too far from my neighbors: fly closer” or “I am too close to my right-hand neighbor; fly left”) and the overarching feedback loop shown in Figure 19, resulting in the concomitant aerial oscillations. Craig Reynolds and other researchers have used the 3 group movement rules to create convincing computer simulations of murmuration (Reynolds, 2017.)

Figure 21. Examples of Bird Murmuration

Black Holes. One of the more interesting natural patterns is that of a black hole (Figure 22), where a reinforcing feedback loop generates a natural singularity. Cosmologists estimate that there are billions of black holes in the universe. The black hole displays radial symmetry in one plane and the singularity in the perpendicular plane. The feedback loop is caused by the interactions of gravity and mass: gravity draws in more mass, the increased mass increases the gravitational force (spatial distortion), which (in turn) draws in even more mass, as shown in Figure 23.

Figure 22. Black Hole

Figure 23. The Black Hole Reinforcing Feedback Loop

This is an example of a natural reinforcing feedback loop run to the extreme. Smolin (1999) speculates that each black hole contains a new universe that may generate new black holes in a never-ending reinforcing feedback loop and pattern of new universe generation.

Kelvin-Helmholz Clouds. These clouds (Figure 24) form when 2 stratified air layers of different densities move horizontally at different relative velocities, creating shear at the interface. The dryer, faster-moving upper layer typically scoops up pieces of the lower, denser cloud layer and captures them in a vortex, as shown in Figure 25 (after Smyth and Moum, 2012.)

Figure 24. Kelvin-Helmholz Clouds

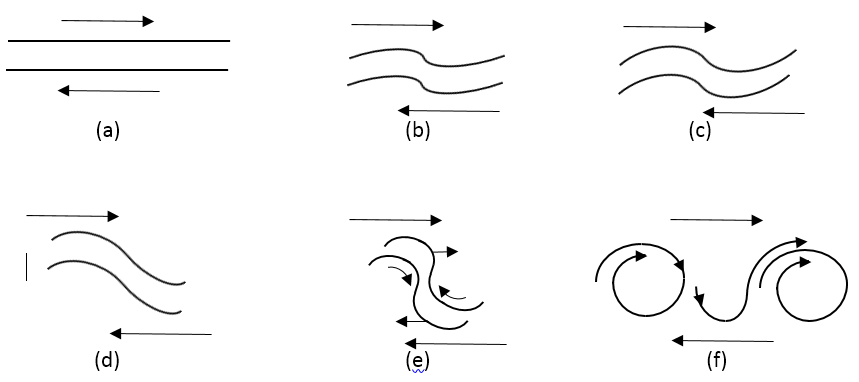Figure 25. The Formation of Kelvin-Helmholz Clouds

The vortex develops into a cylindrical (horizontal axis) rotating cloud (reminiscent of a breaking ocean wave), but it dissipates due to turbulent mixing and evaporation; and another one forms downstream. Some believe that these clouds were the inspiration for Van Gogh’s “Starry Night.” The feedback loop in this case (Figure 26) is reinforcing:

Figure 26. Reinforcing Feedback Loop for Kelvin-Helmholz Cloud Formation

This is another example of a reinforcing feedback loop that is interrupted (this time by turbulence and mixing), to start again.

Ocean waves (Figure 27) follow a similar mechanism, except that the 2 fluid layers are air and water, and because of the higher density of water, gravity plays a bigger role in causing the waves to break, thus interrupting the reinforcing feedback loop that is attempting to create vortices.

Figure 27. Pattern of Ocean Waves in a Line

Space does not permit a detailed explanation of every natural pattern; however Figure 28 shows some more that may also be understood through the application of Systems Thinking.

Figure 28. Additional Natural Patterns

7. Patterns Deriving from Man’s Activities

Although this paper focuses on natural patterns, there are many patterns that derive from man’s activities. Traffic patterns (especially traffic jams; Figure 29) are 1-dimensional versions of the herding/schooling/flocking behavior observed in animals. Drivers are following 2 basic opposing rules: 1) get to my destination as fast as possible and 2) don’t have an accident. These basic mental models translate to a “safe” speed (which is a function of the space between cars) and a “safe” following distance (which is a function of the speed) in a stabilizing feedback loop. When traffic piles up in a jam, the pattern from above appears as a backwards-travelling wave of denser-packed cars moving through the line of traffic.

Figure 29. Traffic Jam

The network pattern deriving from American city location (Figure 30) is also based on opposing forces in a feedback loop. One force that drives cities to form is the availability of human and natural resources, good transportation, and an attractive business and living environment. Competition for those resources limits the size of cities and enforces a degree of separation.

Figure 30. Pattern of U. S. Cities

8. The Structure of the Universe

There are several repeated patterns in the universe, from the pinwheel shape of spiral galaxies to the patterns of planets orbiting their sun and moons orbiting their planets. Systems Thinking teaches us that patterns are caused by underlying structure, which (in turn) is caused by underlying forces. These concepts are useful in understanding those patterns.

The universe appears to be hierarchic: planets (some with moons) embedded within solar systems, solar systems within galaxies, and galaxies in clusters, and these basic structures are repeated many times. Can Systems Thinking and the underlying forces of gravity, electromagnetism, centrifugal, and the nuclear forces explain the structure of the universe, and is the universe self-organizing?

As an example, consider the repeating pinwheel pattern of spiral galaxies in which the shape of each curved radial arm is repeated many times (Figure 31). This pattern is formed by 2 opposing forces: centripetal force F_c (F_c = mv²/r) and gravity F_g (F_g = GMm/r²) where m=the mass of a galactic star, v=the tangential velocity of the star, G= the universal gravitational constant, M = the mass of the galaxy (concentrated at its center), and r= the radial distance of the star from the center of mass. F_g and F_c must be balanced, or else the stars would either all collapse into the galactic center or fly out of orbit and leave the galaxy. If one equates these 2 forces, one obtains the equation v=(GM)^.5/r^.5 which indicates that the tangential velocity of a star in the galaxy is proportional to the square root of the reciprocal of the star’s distance from the center of the galaxy: that is, more distant stars revolve more slowly¹. Over time, the more distant stars lag behind the closer stars in their counter-clockwise motion around the galaxy’s center of gravity. The result is the classic pinwheel shape shown in Figure 31.

Figure 31. Spiral Galaxy NGC 4414

This same analysis applies to solar systems: more distant planets revolve more slowly around the sun (Figure 32). It also applies to moons circling a planet. Jupiter’s moons, for example, precisely follow the inverse square-root law of orbital velocity predicted by Keplerian mechanics.

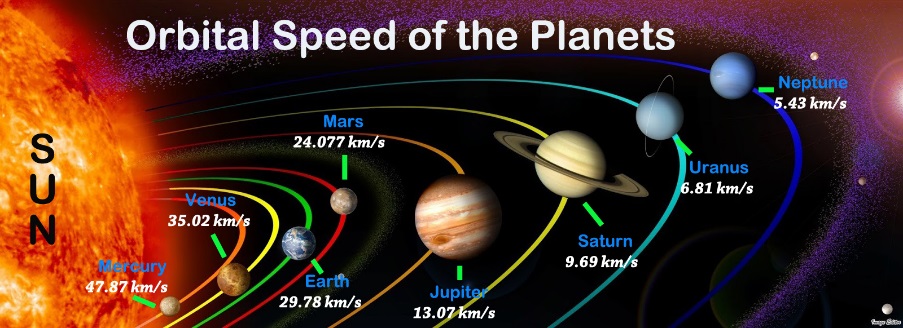Figure 32. Orbital Speeds of Planets

These self-organized patterns are thus the result of gravity (F_g) and centrifugal (F_c) forces acting in opposition. The underlying forces establish a stabilizing feedback loop that keeps them balanced: if, due to some random perturbation, the orbiting body moves closer to (or farther from) its central mass, its orbital velocity will increase (or decrease) so that F_c = F_g as shown in Figure 33.

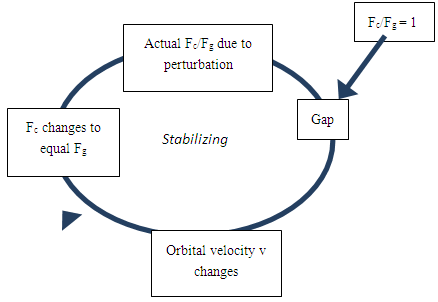Figure 33. Stabilizing Feedback Loop of Orbital Mechanics

But why do spiral galaxies display an azimuthal oscillation of star density structured as several curved arms extending from the nucleus? Each arm is believed to be a region of concentrated new star formation with a greater density of bigger, brighter stars than the inter-arm regions. Gerola and Seiden (1978) believe that stars self-propagate in a reinforcing feedback loop. When a massive star explodes in a supernova, the resulting shock wave triggers star formation in the nearby stellar medium. The newly formed stars live out their lives and also eventually explode in supernovae, propagating more new stars in a chain reaction. But after each star explodes, the local region is too hot for the interstellar gas to condense to form new stars. So each region alternatively experiences new star formation followed by a period of quiescence, until it cools sufficiently to again allow new star formation. If one were to view the galaxy from above over billions of years, one would see various regions blinking on and off as bright regions seem to ignite their neighbors and then go dark. Gerola and Seiden have shown that due to the differential rotation of the galaxy, each star-forming region stretches into a curve. Over time, these brighter curved regions seem to coalesce into spiral arms.

This reinforcing feedback loop of star formation is supported by a closely-related stabilizing feedback loop: interstellar gas and dust condense (due to gravity) to form stars, which (in turn) eventually explode returning their gas and dust to the interstellar medium, where it again can condense into stars. Thus galaxy formation, shape, and stability are controlled by both reinforcing and stabilizing feedback loops acting in concert.

Lee Smolin (1999) hypothesizes a much grander vision of how feedback loops and self-organization impact the structure of our universe; one in which there have been billions of universes, each with different physical laws, some of which were conducive to life and some of which were not. He argues that the same conditions that were conducive to life also generated many stars, which in turn generated many black holes, each of which represented a new universe. In his model, the star-forming universes thus generated many more star-forming universes in a reinforcing feedback loop, while the star-depleted universes died out. Since each new universe has a slightly different set of physical laws, eventually, there was an extremely high probability that a universe materialized that would be full of both stars and life. This vision suggests that the laws of physics (and their concomitant universes) are not fixed, but evolve over time in a form of Darwinian natural selection to a life-supporting universe like the one we inhabit.

Smolin says, “It then seems that our life is situated inside a nested hierarchy of self-organized systems that begin with our local ecologies and extend upwards at least to the galaxy. Each of these levels are non-equilibrium systems (open and active) that owe their existence to processes of self-organization, that are in turn driven by cycles of energy and materials in the level about them. It is then tempting to ask if this relationship extends further than the galaxy. … Must there be a non-equilibrium system (open and active) in which sits our galaxy? Is there a sense in which the universe as a whole could be a non-equilibrium, self-organized system?”

These intriguing Systems Thinking theories suggest that naturally occurring feedback loops and their underlying forces yielded a universe that is self-organized, hierarchical, and full of the structures and patterns that we observe.

9. The Origins of Life on Earth

DNA forms a beautiful double helix molecular pattern (Figure 34) with a basic phosphate-ribose-base structure repeating millions of times. Could Systems Thinking concepts, specifically hierarchical system evolution and molecular self-organization, explain the origins of life on earth? Conventional wisdom argues that a DNA-like precursor was the first form of reproductive life. Sir Fred Hoyle and Chandra Wickramasinghe (1981) have demonstrated the statistical improbability of all the elements in the Archean environment randomly coming together in just the right sequence to form a molecule of DNA (which comprises millions of atoms.) But was it truly random? Inspection reveals that the DNA molecule is hierarchic, with 3 repeating fairly simple sub-units: a phosphate group, a ribose (sugar) group, and a base (adenine, cytosine, thymine, or guanine) connected in a chain and mated to a complementary chain in a double helix. Could a complex DNA molecule have evolved from these much simpler sub-units? The probability of DNA self-organization increases dramatically if its evolution is split into stages: 1) self-organization of each of the 3 basic sub-units independently followed by 2) self-organization of those sub-units into a section of DNA, and then 3) the linking of many such sections to form a long molecule. Scientists have been able to demonstrate the self-organization of amino acids, the sugar, the phosphate, and some of the base groups from a primordial soup of base chemicals (Miller and Urey (1953 and 1959), Oro (1960 and 1961), Keller, Turchyn, & Ralser (2014)), but they have not yet succeeded in demonstrating the self-organization of those constituents into a nucleotide. But self-replication of inanimate chemical structures has been demonstrated. Self-replicating chemical systems (Fulvene, Rotaxone) are well-known to scientists, and Eigen has explored autocatalytic sets of reactions that may be responsible for the self-organization of life (Eigen, 1971). His hypercycle (a reinforcing feedback loop) describes a closed loop of self-replicating molecules, each one of which catalyzes the creation of its successor (see Figure 35). Eigen successfully demonstrated that this chemical cycle displays Darwinian natural selection at the molecular level (Bahnzhaf, 2010.)

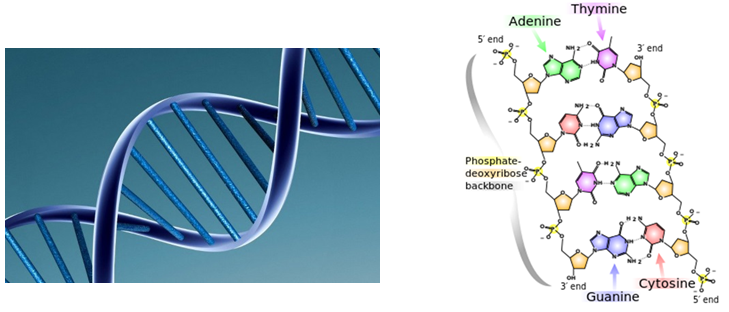Figure 34. Pattern of DNA

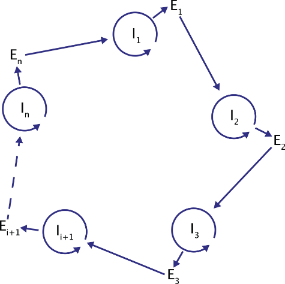Figure 35. The Hypercycle. Reproduced from Eigen & Schuster (1979). Ei = an enzyme and Ii = an RNA matrix. Each enzyme increases the replication rate of its subsequent RNA

There is a plethora of underlying mechanisms and feedback loops responsible for DNA formation and function, operating in a symphony of self-organization. DNA replication is started by an initiator protein (DnaA) which seeks out those inter-base sites where the hydrogen bonds are weakest to start the cleaving of the double helix. (There are also inhibitor proteins to stop this activity.) This is followed by successive waves of Adenosine Tri-Phosphate (ATP) binding, hydrolysis, and release (acting in a feedback loop) causing the helicase enzyme to slide along the DNA molecule and unzip it. Subsequently, hydrogen bonding causes free bases in solution to bind to the single DNA strand, but adenine binds only with thymine and guanine binds only with cytosine due to the physical structure of those molecules. They fit together in a “lock-and-key” mechanism as shown in figure 36. In this feedback loop, hydrogen bonding is the attractive force while the physical shapes deter bonding.

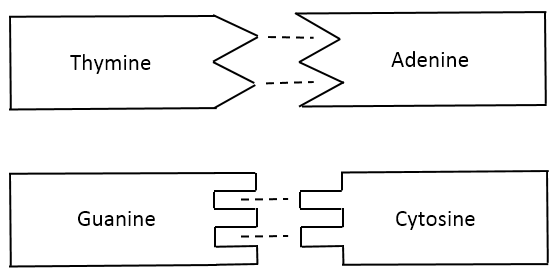Figure 36. The “Lock-and-Key” Mechanism for Base Pair Bonding in DNA

There are many feedback loops associated with DNA. Systems Thinking helps explain the self-organized structures and underlying physical, electrical, and chemical forces that yield DNA’s structure and function.

10. Discussion

Natural patterns confront us every day. Many seem to defy understanding. However, if one realizes that patterns represent physical, temporal, chemical, or emotional oscillations, it becomes easier to fathom them.

There have been previous attempts to explain natural patterns. D’Arcy Wentworth Thompson (1917) argued that physical laws and mechanics play a vital role in determining the structure and morphology of organisms. His main thrusts, however, seem to be to try to explain the evolution of living organisms using mathematics and the morphology of distortion; he never explains animal behavior, non-biological morphologies, or the feedback loops that yield oscillations and patterns.

In his seminal paper, Alan Turing (1952) developed the reaction-diffusion mechanism to explain patterns in living organisms based on chemical and physical laws. He states, “The theory does not make any new hypotheses; it merely suggests that certain well-known physical laws are sufficient to account for many of the facts.” He comes close to the systems thinking philosophy (and indeed articulates several elements of it) but doesn’t integrate them into a broadly-applicable theory; specifically he does not explain inanimate or behavior patterns.

Mano (2004) does a nice job explaining natural patterns as a result of self-organization, as well as the advantages of self-organization, but he does not invoke feedback loops or detail the biological, chemical, and physical mechanisms that yield self-organization. He also suggests that the patterns we see were “stumbled upon” by chance. He proposes self-organization as a solution to a biological problem: “One of the mysteries of biology is how the enormous amount of morphogenic, physiological and behavioral complexity of living organisms can be achieved with the limited amount of genetic information available within the genome. Self-organization is one solution to this problem………… Through self-organization, evolution has stumbled upon a wide range of extremely efficient, relatively simple solutions for solving very complex problems.”

In his ground-breaking book The Life of the Cosmos, Lee Smolin (1999) hypothesizes that our entire universe is a self-organized system, rife with feedback loops, hierarchies, and emergent patterns at all scales in galaxies, planetary systems, and atoms. He speculates that the laws of physics (and their concomitant universes) are not fixed, but evolve over time in a form of Darwinian natural selection. Although the book is full of systems thinking concepts, Smolin does not integrate them into an overarching systems thinking framework.

In his beautiful book, Patterns in Nature, Philip Ball (2016) describes dozens of natural patterns, including mud cracks, fern spirals, fractals, animal skin patterns, beehives, herding/schooling patterns, and flow patterns. He attempts to explain each using scientific principles, and he even refers to feedback loops occasionally. But he doesn’t articulate the underlying causality in all these and misses integrating them into an overarching systems theory explanation involving causal loops, feedback, and hierarchies.

Parveen (2017) explains patterns mathematically, arguing that Fibonacci sequences often provide the most efficient light-gathering structures or the highest surface area: volume ratios, but he does not explain how natural systems generate those mathematical structures.

Although these explanations have merit, they miss the integrated theory afforded by Systems Thinking, specifically the theory that emergent patterns represent oscillations caused by self-organized structure (feedback loops) which in turn, are caused by underlying forces, and that these apply to both living and non-living entities as well as to physical, temporal, emotional, and behavioral patterns. These concepts are the essence of Systems Thinking.

Systems Thinking addresses many questions about natural patterns by invoking concepts such as feedback loops, self-organization, hierarchies, and emergence. However, it also introduces others.

The Nature of the Universe

Ÿ As Lee Smolin (1999) suggests, is our whole universe a complex self-organized system, and can the universe exist and be self-organized without a prime mover?

Ÿ What are the minimum requirements for a universe to self-organize?

Ÿ Are the natural laws such as gravity really laws or are they just properties of the space we inhabit?

The Nature of Life and Self-Awareness

Ÿ Is life itself an emergent property deriving from the self-organization of hierarchical elements?

Ÿ Should our definition of “life” not be binary (either living or not-living) but more a continuum with some threshold beyond which we define as “alive”?

Ÿ Is self-awareness an emergent property of a sufficiently complex self-organized brain, and can any sufficiently complex entity become self-aware?

Ÿ What is the next step of emergence for humanity--the inter-connectedness of all humans into 1 super-being (Monat, 2017)?

These intriguing questions exhort study through the application of Systems Thinking.

11. Conclusions

In this paper, we have explored some of the patterns observed in nature, and used Systems Thinking to explain how and why they came to be. The concepts of feedback loops, hierarchies, self-organization, and emergence contribute to our understanding of these natural patterns. This understanding may help us to influence our natural world in positive ways, and to facilitate the design and improvement of human-designed systems, which is a topic for a future paper.

Note

1. Present-day studies indicate that the tangential velocity of many galactic stars do not follow the inverse square-root law of Keplerian mechanics. This observation has led to the speculation of both the existence of dark matter and a modification to Newton’s law of universal gravitation (Milgrom, 2015). However, all known theories account for the outer galactic stars moving slower than inner stars, although they vary in details.