Salah H. Abid, Heba A. Hassan
Mathematics department, Education College, Al-Mustansiriya University, Baghdad, Iraq
Correspondence to: Salah H. Abid, Mathematics department, Education College, Al-Mustansiriya University, Baghdad, Iraq.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In reliability theory, a combination of two distributions failure rate model for reliability studies is paid much attention. In this paper, we will derive the failure rate model of (Marshall-Olkin Extended Uniform distribution) MOEU 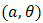 and every one of MOEU
and every one of MOEU 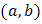 , MOEU
, MOEU 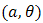 , uniform
, uniform 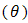 , truncated exponential
, truncated exponential 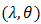 , truncated Weibull
, truncated Weibull 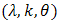 , truncated Frechet
, truncated Frechet 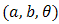 , truncated Rayleigh
, truncated Rayleigh 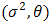 , doubly truncated Cauchy
, doubly truncated Cauchy 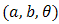 and doublytruncated Gumbel
and doublytruncated Gumbel 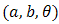 distributions.
distributions.
Keywords:
Reliability, MOEU, Additive rate model, Truncated distribution
Cite this paper: Salah H. Abid, Heba A. Hassan, Some Additive Failure Rate Models Related with MOEU Distribution, American Journal of Systems Science, Vol. 4 No. 1, 2015, pp. 1-10. doi: 10.5923/j.ajss.20150401.01.
1. Introduction
In reliability studies, combinations of components forming series, parallel and k out of n systems are quite popular. The reliability probabilities of such systems are evaluated either by the system as a whole or through the reliability probabilities of the components that define the system. It is well known that in a series system of a finite number of components with independent life time random, the system reliability is equal to the product of the component reliabilities.If 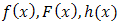 respectively indicate the failure density, failure probability and failure rate of a component with life time random variable x, then we know that the reliability is given by,
respectively indicate the failure density, failure probability and failure rate of a component with life time random variable x, then we know that the reliability is given by,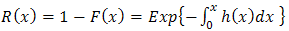 | (1) |
Where 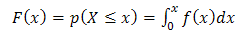 | (2) |
If a series system has two component with independent but non-identical life patterns explained by two distinct random variables say 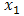 and
and 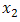 with respective failure densities, failure probabilities and failure rates as
with respective failure densities, failure probabilities and failure rates as 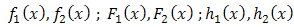 , then the system reliability is given by,
, then the system reliability is given by,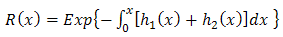 | (3) |
From the above expression we can get the failure density and the failure rate of the series system whose reliability is given by (3), such models are already studied in the past with different choices of 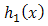 and
and 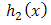 by Rao, Nagendram and Rosaiah (2013), Rao, Kantam, Rosaiah and Baba (2013) [4] and Rosaiah, Nagarjuna, Kumar and Rao (2014) [3]. In this paper a combination of
by Rao, Nagendram and Rosaiah (2013), Rao, Kantam, Rosaiah and Baba (2013) [4] and Rosaiah, Nagarjuna, Kumar and Rao (2014) [3]. In this paper a combination of 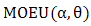 and some other distributions will studied.
and some other distributions will studied.
2. MOEU Distribution and Its Properties
Marshall and Olkin (1997) [2] introduced a new family of distributions in an attempt to add a parameter to a family of distributions. Let 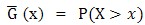 be the reliability function of a random variable X and
be the reliability function of a random variable X and 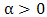 be a parameter. Then
be a parameter. Then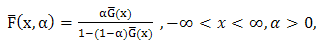 | (4) |
is a proper reliability function. 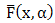 is called Marshall-Olkin family of distributions. The probability density function (p.d.f) corresponding to (4) is given by
is called Marshall-Olkin family of distributions. The probability density function (p.d.f) corresponding to (4) is given by 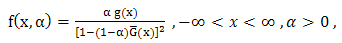 | (5) |
where 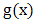 is the p.d.f. corresponding to
is the p.d.f. corresponding to 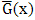 . The hazard (failure) rate function is given by
. The hazard (failure) rate function is given by 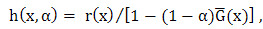 where
where 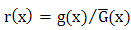 .Now, Let X follows
.Now, Let X follows 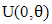 distribution, where
distribution, where 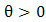 . Then
. Then 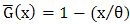 . Substituting in (1) we get a new distribution denoted by MOEU
. Substituting in (1) we get a new distribution denoted by MOEU 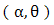 with reliability function [1].
with reliability function [1].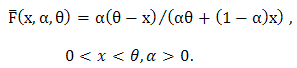 | (6) |
The corresponding pdf is obtained as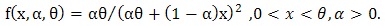 | (7) |
and the corresponding cumulative distribution function is,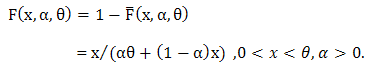 | (8) |
Note that 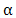 is the shape parameter and
is the shape parameter and 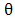 is the scale parameter of the distribution. The hazard rate function of a random variable X with MOEU
is the scale parameter of the distribution. The hazard rate function of a random variable X with MOEU 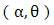 distribution is
distribution is 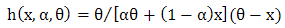 | (9) |
The higher-order moments is [1],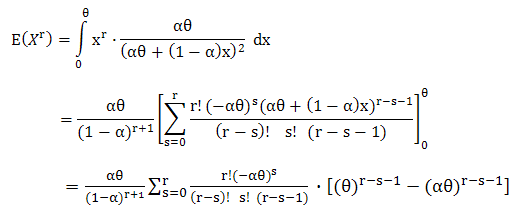 | (10) |
Specially, the mean and the variance of a random variable X with MOEU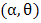 distribution are, respectively [1],
distribution are, respectively [1], 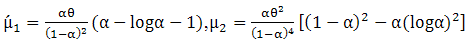 .So, the coefficient of variation is,
.So, the coefficient of variation is, 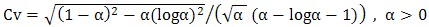 . The
. The 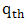 quantile of a random variable X with MOEU
quantile of a random variable X with MOEU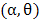 distribution is given by [1],
distribution is given by [1],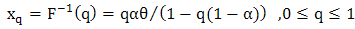 , Where
, Where 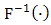 is the inverse distribution function.The median is
is the inverse distribution function.The median is 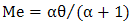 , and the mode is
, and the mode is 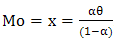 . The skewness is
. The skewness is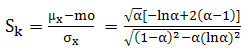 and the kurtosis is
and the kurtosis is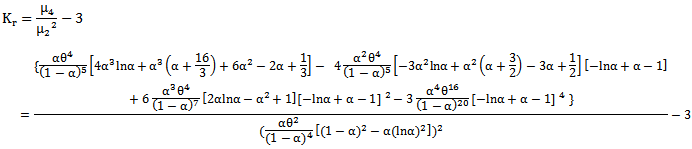 In the following sections we will derive Some additive failure rate models related with MOEU distribution.
In the following sections we will derive Some additive failure rate models related with MOEU distribution.
3. MOEU-MOEU Additive Failure Rate Model
Here we choice 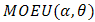 for
for 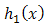 and
and 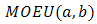 for
for 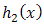 , then
, then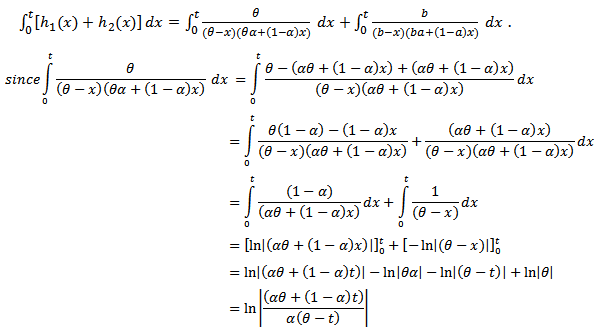 | (11) |
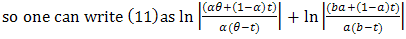 , and then by (3) can get,
, and then by (3) can get, 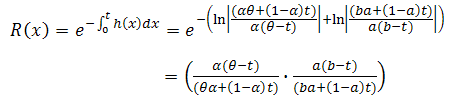 | (12) |
Which is mean, 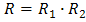 . So for two additive failure rates,
. So for two additive failure rates, 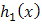 of
of 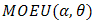 and
and 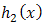 of
of 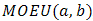 , one can get the distribution of the system as.
, one can get the distribution of the system as. 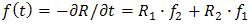 , where,
, where,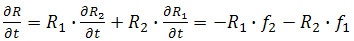 , so,
, so, 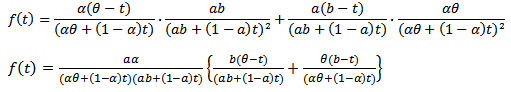 | (13) |
According to the same argument, if we have for two additive failure rates 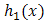 of
of 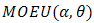 and
and 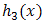 of
of  , then, one can get the distribution of the system as.
, then, one can get the distribution of the system as.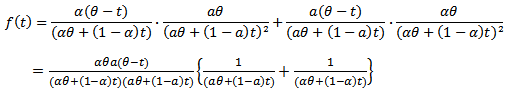 | (14) |
4. MOEU-Uniform Additive Failure Rate Model
Here we choice 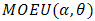 for
for 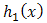 and
and 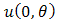 for
for 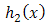 . So, Since
. So, Since 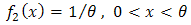 , then
, then 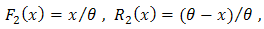 and
and 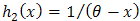 . We have,
. We have, 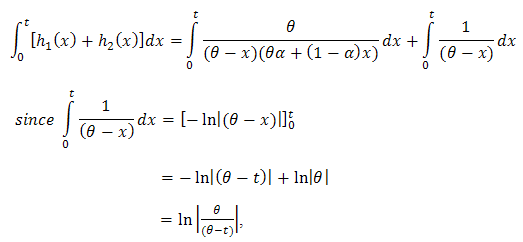 then we get,
then we get,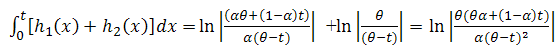 So, by (3), one can get the system Reliability as,
So, by (3), one can get the system Reliability as,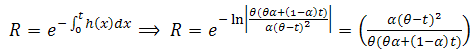 | (15) |
For two additive failure rates, 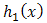 of
of 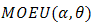 and
and 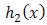 of
of 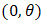 , then, one can get the distribution of the system as.
, then, one can get the distribution of the system as.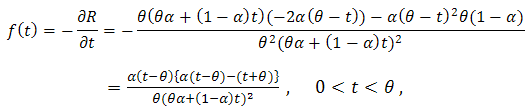 | (16) |
5. MOEU-Truncated Exponential Additive Failure Rate Model
The probability density function of truncated exponential distribution from the right can be derived as,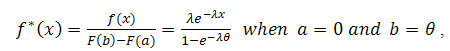 so the cumulative distribution is
so the cumulative distribution is 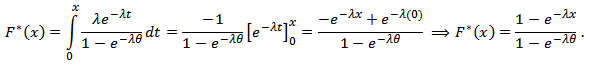 and then the reliability function is
and then the reliability function is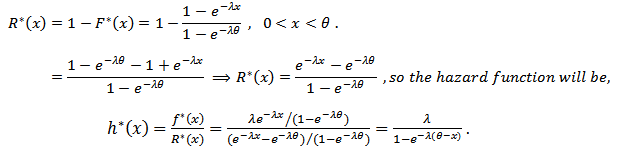 | (17) |
Here we choice 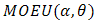 for
for 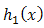 and truncated exponential from the right for
and truncated exponential from the right for 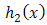 .Now, since
.Now, since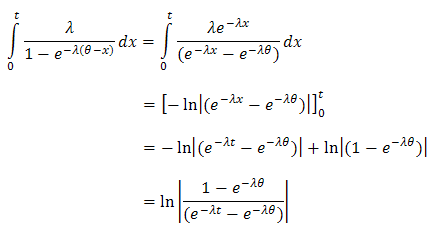 So, we can write
So, we can write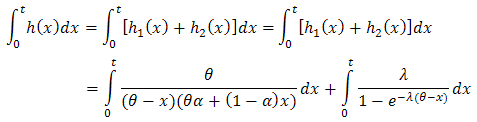 We get
We get 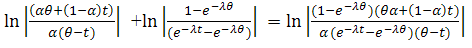 And then the reliability function of the system can be written by (3) as,
And then the reliability function of the system can be written by (3) as,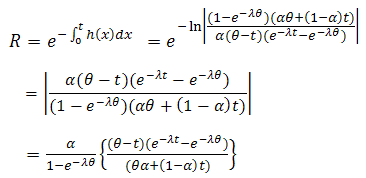 | (18) |
It follows that, for two additive failure rates 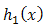 of
of 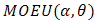 and
and 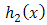 of truncated exponential (λ) at, then one can get the distribution of the system as follows,
of truncated exponential (λ) at, then one can get the distribution of the system as follows,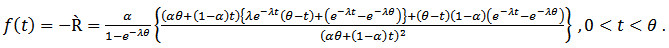 | (19) |
Where, 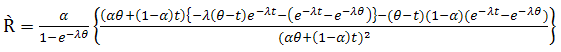
6. MOEU-Truncated Weibull Additive Failure Rate Model
The pdf of the truncated Weibull from the right at 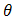 can be derived as
can be derived as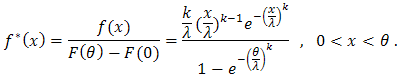 so, the distribution function can be defined as
so, the distribution function can be defined as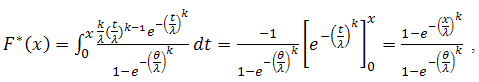 and then the reliability function will be,
and then the reliability function will be,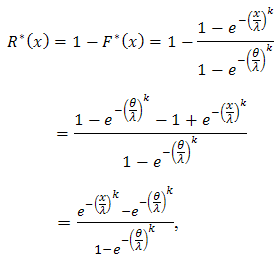 so the failure rate function will be,
so the failure rate function will be,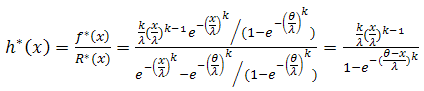 | (20) |
So if we choice 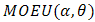 for
for 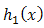 and truncated Weibull
and truncated Weibull 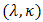 from the right at
from the right at 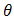 for
for 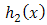
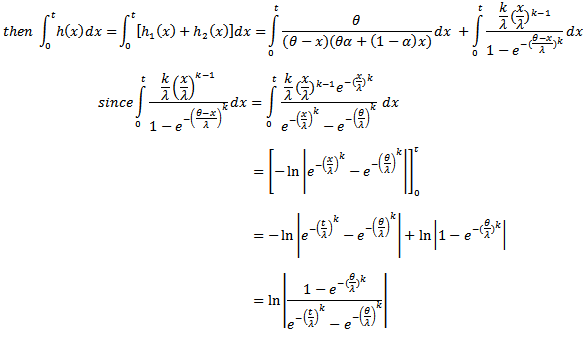 Then
Then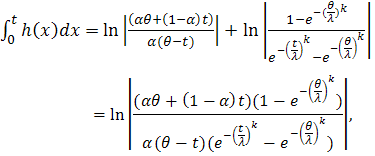 so by (3) the reliability function of the system is,
so by (3) the reliability function of the system is,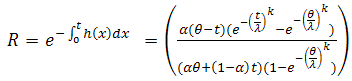 | (21) |
for two additive failure rates, 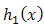 of
of 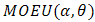 and
and 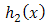 of truncated weibull
of truncated weibull 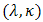 from the right at
from the right at 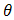 , then, one can get the distribution of the system as,
, then, one can get the distribution of the system as,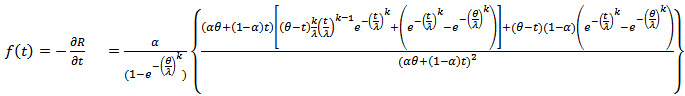 | (22) |
7. MOEU-Truncated Frechet Additive Failure Rate Model
The pdf of truncated Frechet from the right at 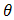 can be derived as,
can be derived as, 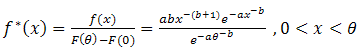 . so the distribution function can be derived as,
. so the distribution function can be derived as,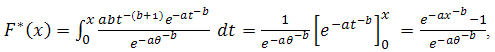 and then the reliability function as,
and then the reliability function as, 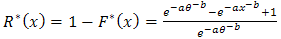 So the hazard function will be
So the hazard function will be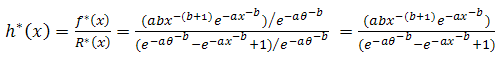 | (23) |
Now, if we choice 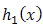 of
of 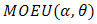 and
and 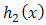 of truncated Frechet
of truncated Frechet 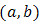 from the right at,
from the right at,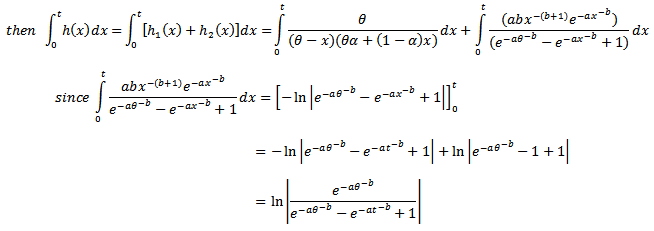 Then
Then 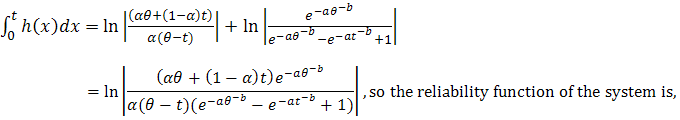
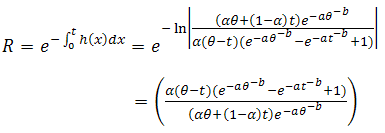 | (24) |
For two additive failure rates 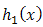 of
of 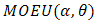 and
and 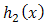 of truncated Frechet
of truncated Frechet 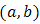 , then, one can get the probability distribution of the system as,
, then, one can get the probability distribution of the system as,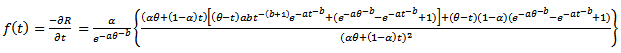 | (25) |
8. MOEU-Truncated Rayleigh Additive Failure Rate Model
The pdf of truncated Rayleigh from the right at 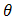 can be derived as,
can be derived as,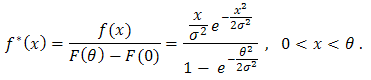 so the distribution function is,
so the distribution function is,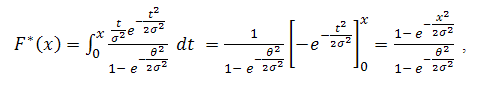 and the reliability function is,
and the reliability function is,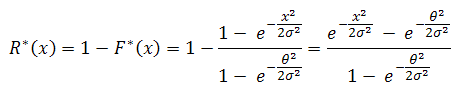 So, the hazard function will be
So, the hazard function will be 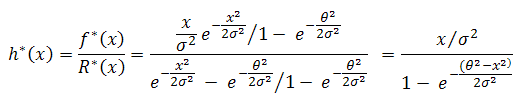 Now, if we choice
Now, if we choice 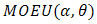 for
for 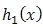 and truncated Rayleigh
and truncated Rayleigh 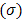 from the right at
from the right at 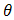 for
for 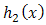 then,
then, 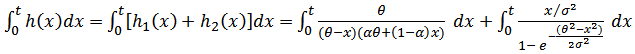
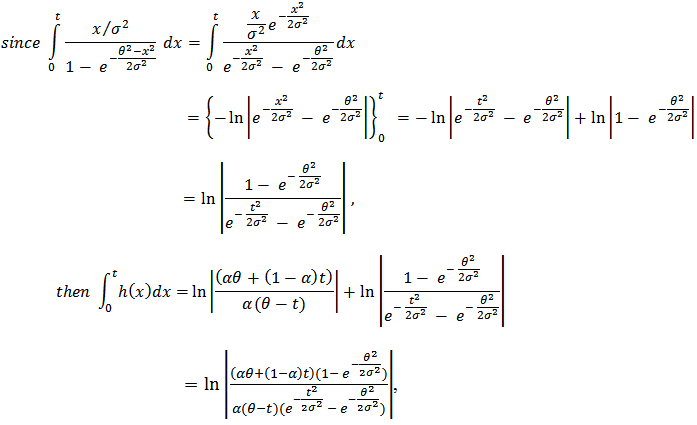 so the reliability function of the system is ,
so the reliability function of the system is ,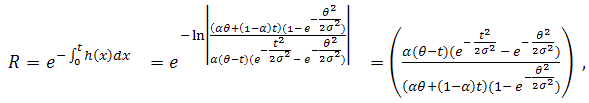 | (26) |
For two additive failure rates, 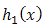 of
of 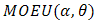 and
and 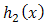 of truncated Rayleigh
of truncated Rayleigh 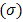 from the right at
from the right at 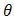 then, one can get the distribution of the system as,
then, one can get the distribution of the system as,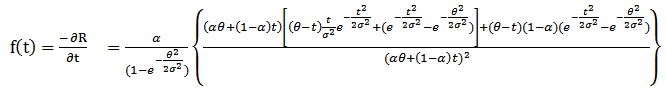 | (27) |
9. MOEU- Doubly Truncated Cauchy Additive Failure Rate Model
The pdf of doublytruncated Cauchy from the right at 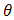 and from the left at zero can be derived as,
and from the left at zero can be derived as,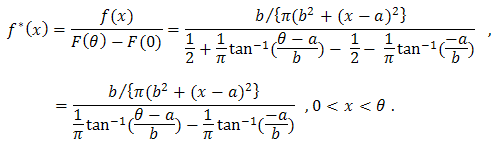 So the distribution function is
So the distribution function is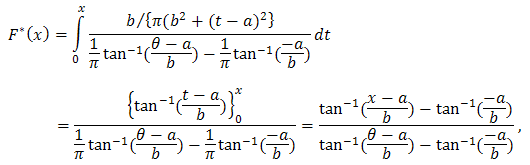 And the reliability function is
And the reliability function is 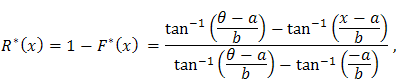 and then the hazard function will be,
and then the hazard function will be,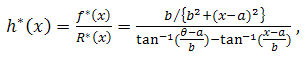 | (28) |
Now, if we choice 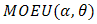 for
for 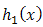 and doublytruncated Cauchy
and doublytruncated Cauchy 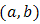 from the right at
from the right at 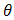 and from the left at zero for
and from the left at zero for 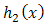 then,
then, 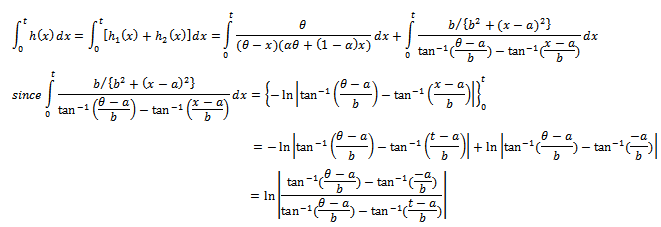 Then,
Then,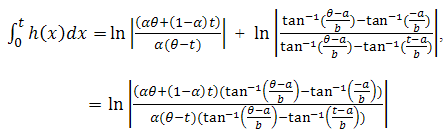 | (29) |
So, the reliability of the system can be written as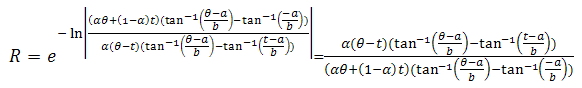 | (30) |
So, for two additive failure rates, 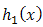 of
of 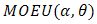 and
and 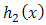 of doublytruncated Cauchy
of doublytruncated Cauchy 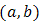 from the right at
from the right at 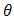 and from the left at zero, one can get the distribution of the system as
and from the left at zero, one can get the distribution of the system as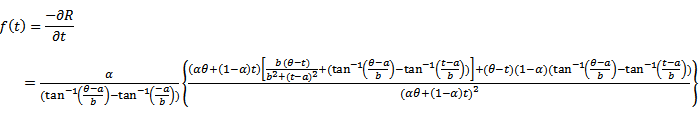 | (31) |
10. MOEU-Doublytruncated Gumbel Additive Failure Rate Model
The pdf of doublytruncated Gumbel from the right, at 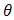 and from the left at zero, can be derived as,
and from the left at zero, can be derived as, 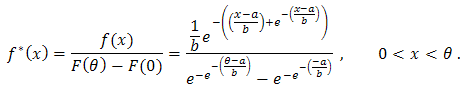 So the distribution function is
So the distribution function is 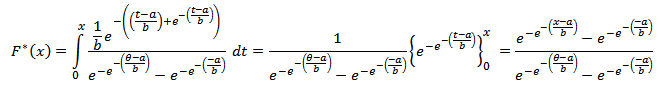 And the reliability function is
And the reliability function is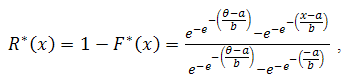 and then the hazard function will be
and then the hazard function will be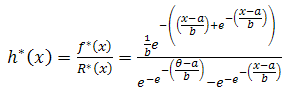 | (32) |
Now, if we choice 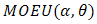 for
for 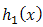 and doublytruncated Gumbel(a,b) from the right at
and doublytruncated Gumbel(a,b) from the right at 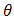 and from the left at zero for
and from the left at zero for 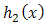 then,
then, 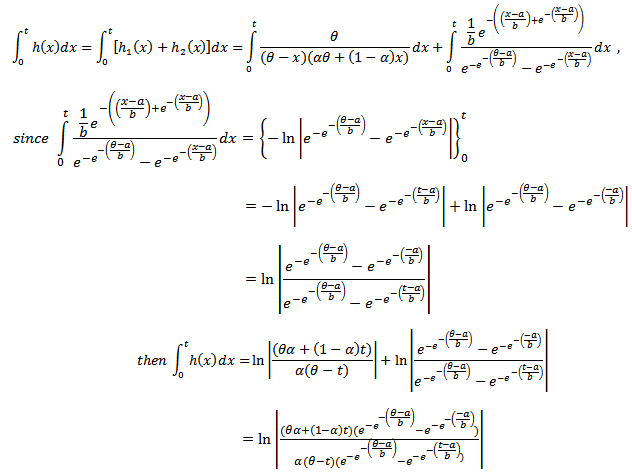 | (33) |
So the reliability function of the system can be written as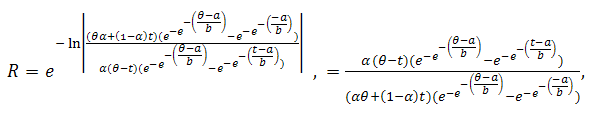 | (34) |
For two additive failure rates, 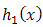 of
of 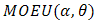 and
and 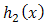 of doublytruncated Gmbel(a,b) from the right at
of doublytruncated Gmbel(a,b) from the right at 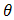 and from the left at zero, one can get the distribution of the system as.
and from the left at zero, one can get the distribution of the system as.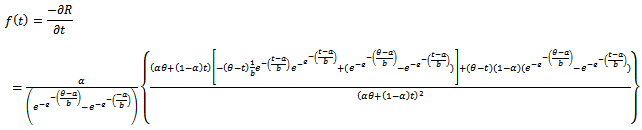 | (35) |
11. Summary and Conclusions
In spite of the great importance of the uniform distribution uses, but unfortunately the form of the distribution and its properties reduced the distribution applications, especially in real life. This issue has made us think to construct other distributions based on the uniform distribution, So that the new distributions have flexible forms and properties to represent a lot of other applications.A combination of (Marshall-Olkin Extended Uniform distribution) MOEU 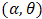 model and every one of some probability models are developed on lines of the well known linear failure rate model .We derive here the additive failure rate model of MOEU
model and every one of some probability models are developed on lines of the well known linear failure rate model .We derive here the additive failure rate model of MOEU 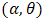 and every one of MOEU
and every one of MOEU 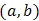 , MOEU
, MOEU 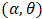 , uniform
, uniform 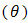 , truncated exponential
, truncated exponential 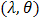 , truncated Weibull
, truncated Weibull 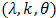 , truncated Frechet
, truncated Frechet 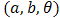 , truncated Rayleigh
, truncated Rayleigh 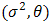 , truncated Cauchy
, truncated Cauchy 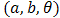 and truncated Gumbel
and truncated Gumbel 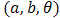 distributions.
distributions.
References
| [1] | Abid, Salah H. and Hassan, Heba A. (2015) "The Marshall-Olkin extended Uniform stress- strength model", American Journal of Math. and Stat. ,Volume 4, Number 1, p.1-10. |
| [2] | Marshall, A.W., Olkin, I. (1997) "A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families" Biometrika, 84, 641-652. |
| [3] | Rosaiah, K. , Maruthi Nagarjuna, K., Siva Kumar, D. and Srinivasa Rao, B. (2014) "Exponential–Log Logistic Additive Failure Rate Model", International Journal of Scientific and Research Publications, Volume 4, Issue 3, March, p.1-5. |
| [4] | Srinivasa Rao, B., Kantam, R.R.L., Rosaiah, K. and Sridhar Babu, M. (2013) "Exponential–gamma additive failure rate model", Journal of Safety Engineering, 2 (2A), 1–6. |
| [5] | Srinivasa Rao, B., Nagendram, S. and Rosaiah, K. (2013) "Exponential–Half logistic additive failure rate model", International Journal of Scientific and Research, 3(5), p.1-10. |

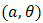 and every one of MOEU
and every one of MOEU 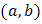 , MOEU
, MOEU 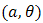 , uniform
, uniform 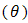 , truncated exponential
, truncated exponential 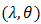 , truncated Weibull
, truncated Weibull 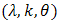 , truncated Frechet
, truncated Frechet 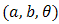 , truncated Rayleigh
, truncated Rayleigh 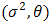 , doubly truncated Cauchy
, doubly truncated Cauchy 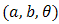 and doublytruncated Gumbel
and doublytruncated Gumbel 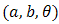 distributions.
distributions.
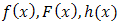 respectively indicate the failure density, failure probability and failure rate of a component with life time random variable x, then we know that the reliability is given by,
respectively indicate the failure density, failure probability and failure rate of a component with life time random variable x, then we know that the reliability is given by,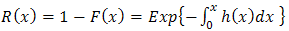
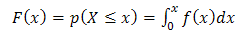
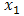 and
and 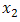 with respective failure densities, failure probabilities and failure rates as
with respective failure densities, failure probabilities and failure rates as 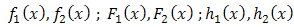 , then the system reliability is given by,
, then the system reliability is given by,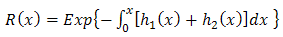
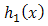 and
and 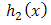 by Rao, Nagendram and Rosaiah (2013), Rao, Kantam, Rosaiah and Baba (2013) [4] and Rosaiah, Nagarjuna, Kumar and Rao (2014) [3]. In this paper a combination of
by Rao, Nagendram and Rosaiah (2013), Rao, Kantam, Rosaiah and Baba (2013) [4] and Rosaiah, Nagarjuna, Kumar and Rao (2014) [3]. In this paper a combination of 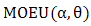 and some other distributions will studied.
and some other distributions will studied. 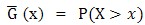 be the reliability function of a random variable X and
be the reliability function of a random variable X and 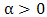 be a parameter. Then
be a parameter. Then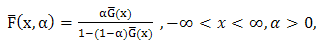
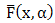 is called Marshall-Olkin family of distributions. The probability density function (p.d.f) corresponding to (4) is given by
is called Marshall-Olkin family of distributions. The probability density function (p.d.f) corresponding to (4) is given by 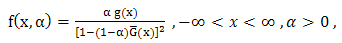
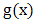 is the p.d.f. corresponding to
is the p.d.f. corresponding to 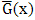 . The hazard (failure) rate function is given by
. The hazard (failure) rate function is given by 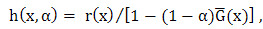 where
where 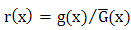 .Now, Let X follows
.Now, Let X follows 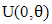 distribution, where
distribution, where 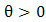 . Then
. Then 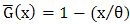 . Substituting in (1) we get a new distribution denoted by MOEU
. Substituting in (1) we get a new distribution denoted by MOEU 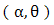 with reliability function [1].
with reliability function [1].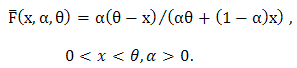
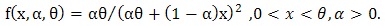
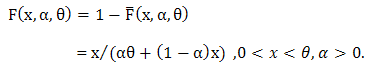
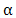 is the shape parameter and
is the shape parameter and 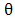 is the scale parameter of the distribution. The hazard rate function of a random variable X with MOEU
is the scale parameter of the distribution. The hazard rate function of a random variable X with MOEU 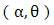 distribution is
distribution is 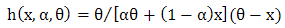
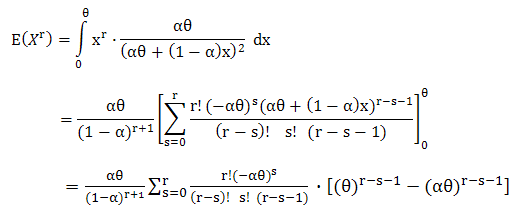
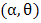 distribution are, respectively [1],
distribution are, respectively [1], 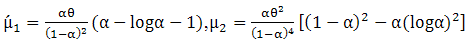 .So, the coefficient of variation is,
.So, the coefficient of variation is, 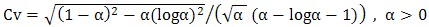 . The
. The 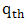 quantile of a random variable X with MOEU
quantile of a random variable X with MOEU distribution is given by [1],
distribution is given by [1],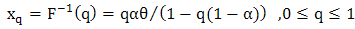 , Where
, Where 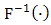 is the inverse distribution function.The median is
is the inverse distribution function.The median is 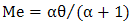 , and the mode is
, and the mode is 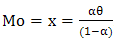 . The skewness is
. The skewness is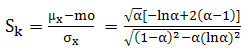 and the kurtosis is
and the kurtosis is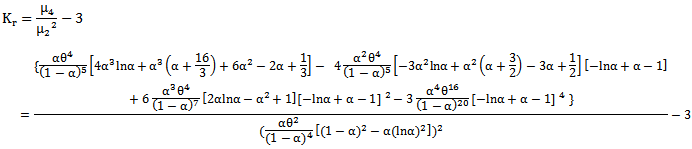 In the following sections we will derive Some additive failure rate models related with MOEU distribution.
In the following sections we will derive Some additive failure rate models related with MOEU distribution. for
for  and
and 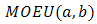 for
for 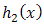 , then
, then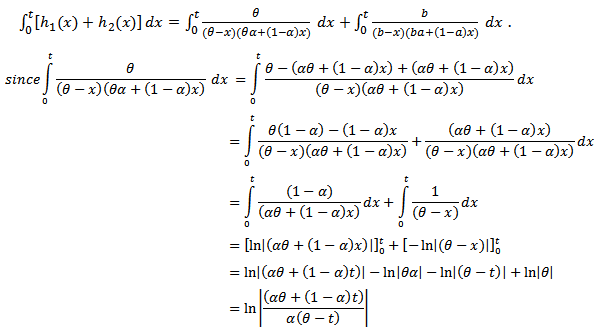
 , and then by (3) can get,
, and then by (3) can get, 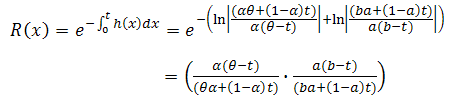
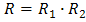 . So for two additive failure rates,
. So for two additive failure rates, 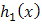 of
of 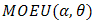 and
and 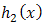 of
of 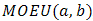 , one can get the distribution of the system as.
, one can get the distribution of the system as. 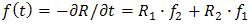 , where,
, where,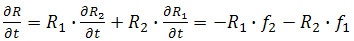 , so,
, so, 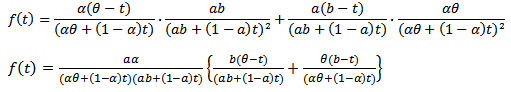
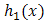 of
of  and
and  of
of  , then, one can get the distribution of the system as.
, then, one can get the distribution of the system as.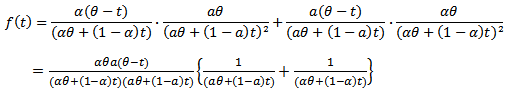
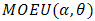 for
for 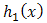 and
and 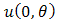 for
for 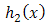 . So, Since
. So, Since 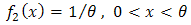 , then
, then 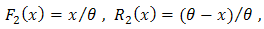 and
and 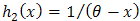 . We have,
. We have, 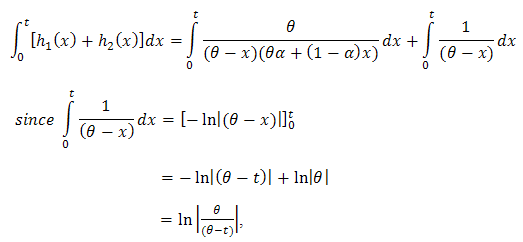 then we get,
then we get,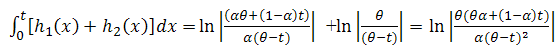 So, by (3), one can get the system Reliability as,
So, by (3), one can get the system Reliability as,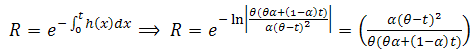
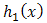 of
of 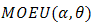 and
and 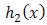 of
of 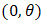 , then, one can get the distribution of the system as.
, then, one can get the distribution of the system as.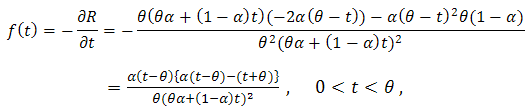
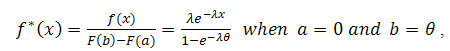 so the cumulative distribution is
so the cumulative distribution is 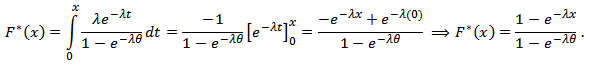 and then the reliability function is
and then the reliability function is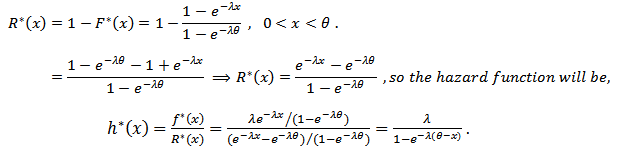
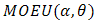 for
for 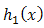 and truncated exponential from the right for
and truncated exponential from the right for 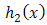 .Now, since
.Now, since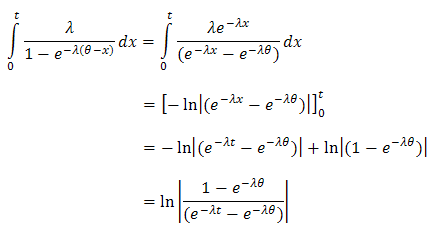 So, we can write
So, we can write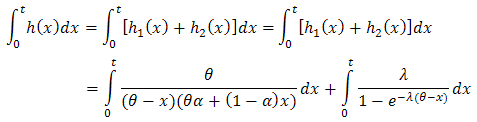 We get
We get 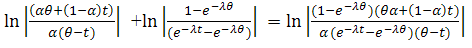 And then the reliability function of the system can be written by (3) as,
And then the reliability function of the system can be written by (3) as,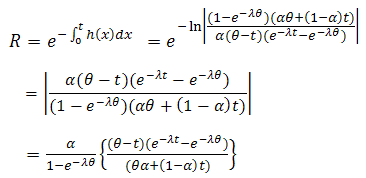
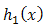 of
of 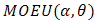 and
and 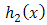 of truncated exponential (λ) at, then one can get the distribution of the system as follows,
of truncated exponential (λ) at, then one can get the distribution of the system as follows,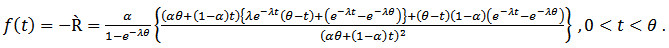
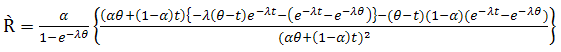
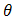 can be derived as
can be derived as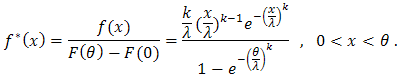 so, the distribution function can be defined as
so, the distribution function can be defined as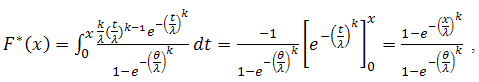 and then the reliability function will be,
and then the reliability function will be,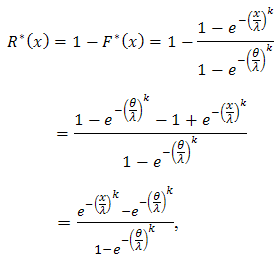 so the failure rate function will be,
so the failure rate function will be,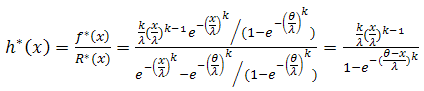
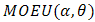 for
for 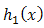 and truncated Weibull
and truncated Weibull 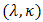 from the right at
from the right at 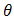 for
for 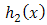
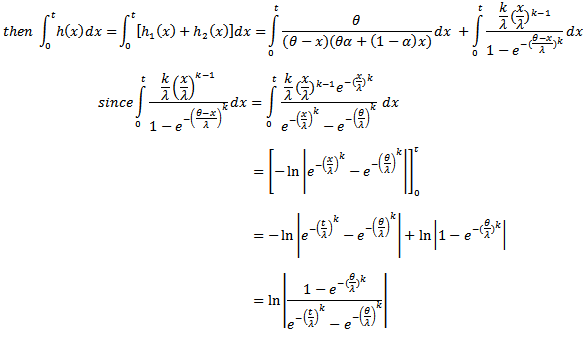 Then
Then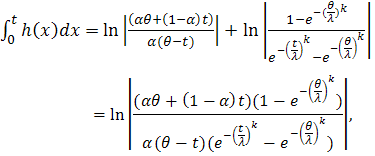 so by (3) the reliability function of the system is,
so by (3) the reliability function of the system is,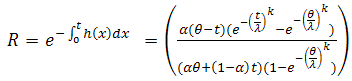
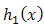 of
of 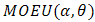 and
and 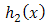 of truncated weibull
of truncated weibull 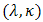 from the right at
from the right at 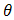 , then, one can get the distribution of the system as,
, then, one can get the distribution of the system as,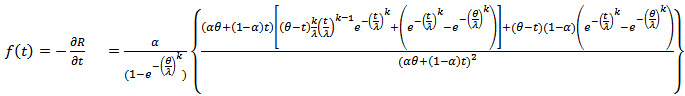
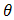 can be derived as,
can be derived as, 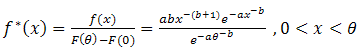 . so the distribution function can be derived as,
. so the distribution function can be derived as,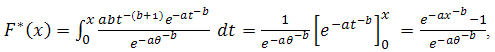 and then the reliability function as,
and then the reliability function as, 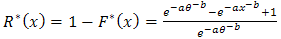 So the hazard function will be
So the hazard function will be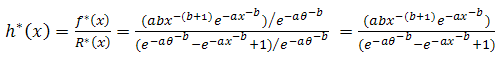
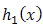 of
of 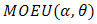 and
and 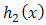 of truncated Frechet
of truncated Frechet 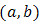 from the right at,
from the right at,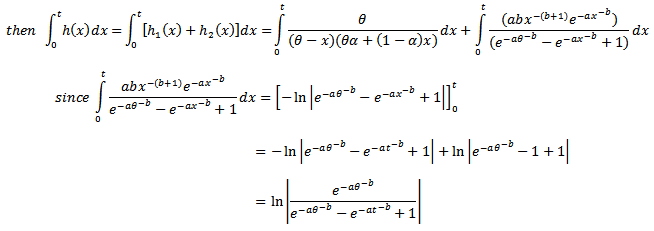 Then
Then 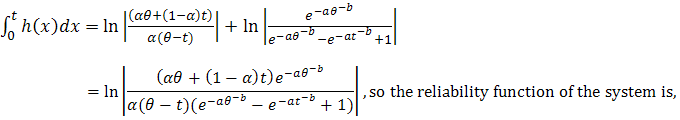
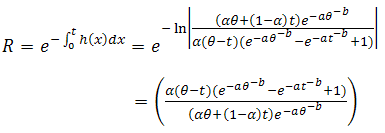
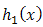 of
of 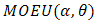 and
and 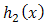 of truncated Frechet
of truncated Frechet 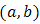 , then, one can get the probability distribution of the system as,
, then, one can get the probability distribution of the system as,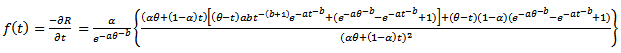
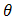 can be derived as,
can be derived as,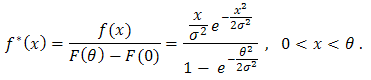 so the distribution function is,
so the distribution function is,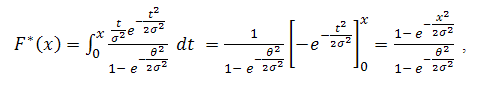 and the reliability function is,
and the reliability function is,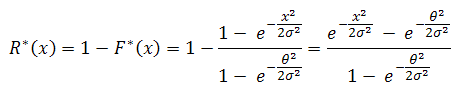 So, the hazard function will be
So, the hazard function will be 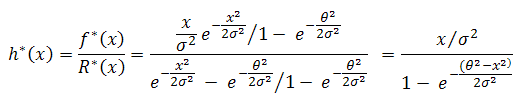 Now, if we choice
Now, if we choice 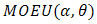 for
for 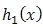 and truncated Rayleigh
and truncated Rayleigh 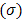 from the right at
from the right at 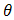 for
for 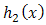 then,
then, 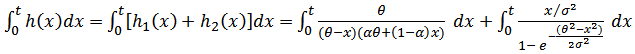
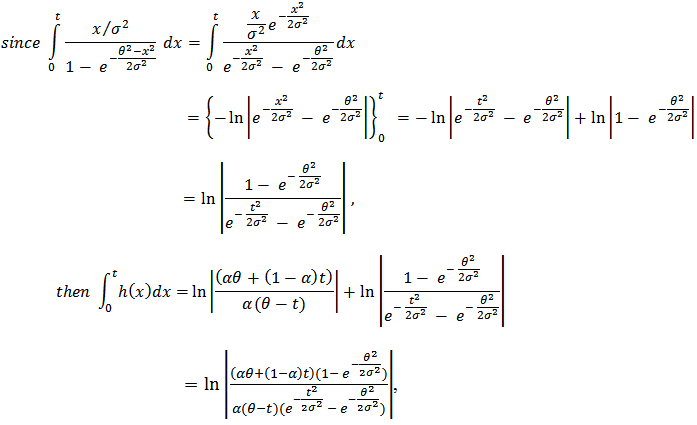 so the reliability function of the system is ,
so the reliability function of the system is ,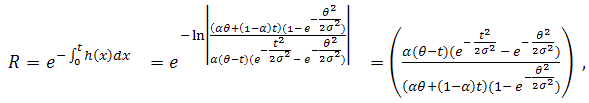
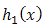 of
of 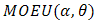 and
and 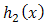 of truncated Rayleigh
of truncated Rayleigh 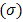 from the right at
from the right at 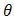 then, one can get the distribution of the system as,
then, one can get the distribution of the system as,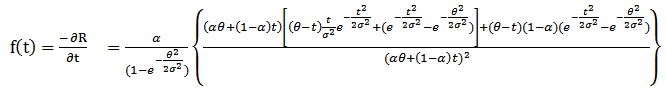
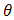 and from the left at zero can be derived as,
and from the left at zero can be derived as,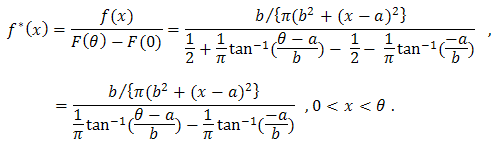 So the distribution function is
So the distribution function is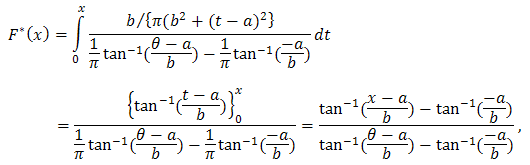 And the reliability function is
And the reliability function is 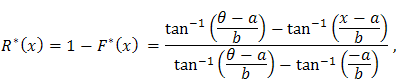 and then the hazard function will be,
and then the hazard function will be,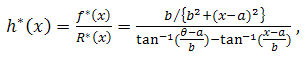
 for
for 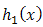 and doublytruncated Cauchy
and doublytruncated Cauchy 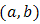 from the right at
from the right at 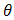 and from the left at zero for
and from the left at zero for 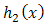 then,
then, 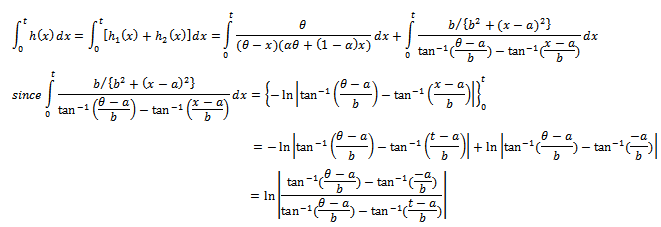 Then,
Then,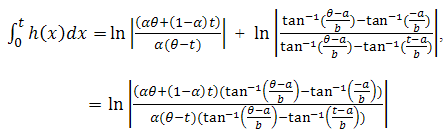
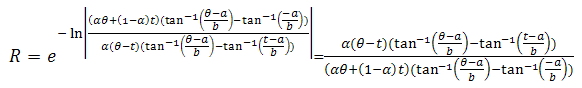
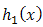 of
of 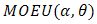 and
and 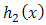 of doublytruncated Cauchy
of doublytruncated Cauchy 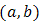 from the right at
from the right at 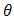 and from the left at zero, one can get the distribution of the system as
and from the left at zero, one can get the distribution of the system as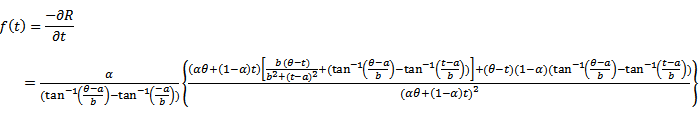
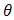 and from the left at zero, can be derived as,
and from the left at zero, can be derived as, 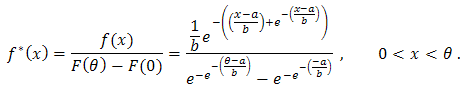 So the distribution function is
So the distribution function is 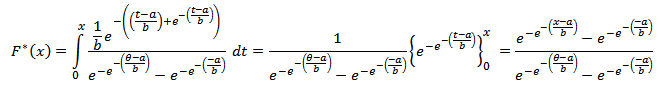 And the reliability function is
And the reliability function is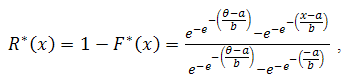 and then the hazard function will be
and then the hazard function will be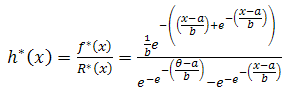
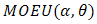 for
for 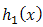 and doublytruncated Gumbel(a,b) from the right at
and doublytruncated Gumbel(a,b) from the right at 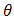 and from the left at zero for
and from the left at zero for 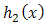 then,
then, 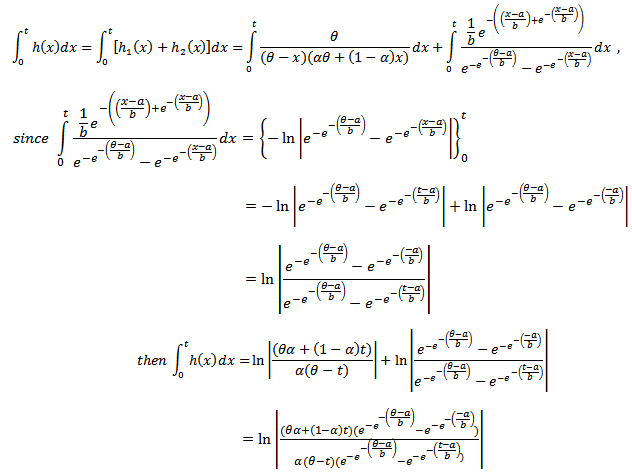
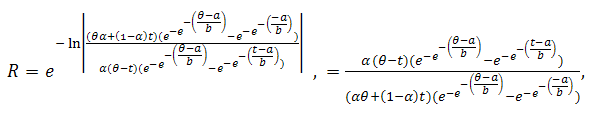
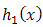 of
of 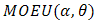 and
and 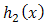 of doublytruncated Gmbel(a,b) from the right at
of doublytruncated Gmbel(a,b) from the right at 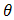 and from the left at zero, one can get the distribution of the system as.
and from the left at zero, one can get the distribution of the system as.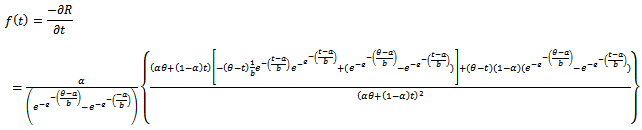
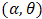 model and every one of some probability models are developed on lines of the well known linear failure rate model .We derive here the additive failure rate model of MOEU
model and every one of some probability models are developed on lines of the well known linear failure rate model .We derive here the additive failure rate model of MOEU 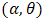 and every one of MOEU
and every one of MOEU 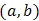 , MOEU
, MOEU 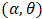 , uniform
, uniform 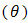 , truncated exponential
, truncated exponential 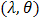 , truncated Weibull
, truncated Weibull 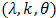 , truncated Frechet
, truncated Frechet 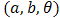 , truncated Rayleigh
, truncated Rayleigh 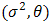 , truncated Cauchy
, truncated Cauchy 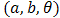 and truncated Gumbel
and truncated Gumbel 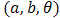 distributions.
distributions. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML