-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2020; 10(1): 10-18
doi:10.5923/j.ajsp.20201001.02

Mitigation of Continuous Wave Narrow-Band Interference in QPSK Demodulation Using Adaptive IIR Notch Filter
Abdelrahman El Gebali, René Jr Landry
Department of Electrical Engineering, École de Technologie Supérieure (ETS), Montréal, Canada
Correspondence to: Abdelrahman El Gebali, Department of Electrical Engineering, École de Technologie Supérieure (ETS), Montréal, Canada.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A Continuous Wave Narrow-Band Interference (CW-NBI) can reduce the effective signal-to-noise ratio (SNR), and the quality of the Signals-of-Interest (SoI) in any wireless transmission such as in a Digital Video Broadcasting (DVB-S2) receiver. Therefore, this paper proposes a novel low-complexity anti-jamming filter to mitigate unknown CW-NBI. The approach is to develop a robust least-mean-squared (LMS) algorithm for mitigating CW-NBI in QPSK demodulation but could be used in any communication system. The proposed filter is based on two open-loop Adaptive lattice Notch Filter (ALNF) structure and an LMS algorithm. Each ALNF is composed of a second-order Infinite-Impulse-Response (IIR) filter. The first ALNF is used to estimate the Jamming to Signal Ratio (JSR) and the frequency of the interference. In contrast, the second ALNF is used to remove the interference and adjust the depth of the notch according to the estimated JSR. On the other hand, the LMS algorithm is used to obtain and then track the interference. Simulation results show the performance of the proposed IIR notch filter with the LMS algorithm in reducing and mitigating interference. Also, it provides better output SNR of the notch filter for a given value of JSR and BER performance. For example, at the JSR value of -6 dB, the SNR output of the proposed IIR notch filter was enhanced by 9 dB compared to the case without a filter when 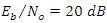 .
.
Keywords: CW-NBI, SNR, QPSK, ANF, ALNF, IIR, LMS, JSR, DVB-S2
Cite this paper: Abdelrahman El Gebali, René Jr Landry, Mitigation of Continuous Wave Narrow-Band Interference in QPSK Demodulation Using Adaptive IIR Notch Filter, American Journal of Signal Processing, Vol. 10 No. 1, 2020, pp. 10-18. doi: 10.5923/j.ajsp.20201001.02.
Article Outline
1. Introduction
- As the telecommunication systems technology is expanding, human-made Radio Frequency Interference (RFI) is continuously increasing. The radio frequency (RF) spectrum is a decisive part of wireless communication. Wireless and satellite systems use the RF spectrum to communicate with ground stations, aircraft, and/or other satellites. As the RF spectrum is a limited resource shared by numerous systems, and taking into account the increasing number of users in terrestrial and space applications, it leads to the RF-crowded spectrum, which is suffering from different unintentional RFI and intentional acts such as jamming. CW-NBI impacts the wireless communications signal at the receiver side, leading to 1) Degradation of the Quality of Service (QoS) of the communication system, 2) Decrease the signal to noise ratio (SNR) and increase the bit error rate (BER), 3) Reduce the quality of the Signals-of-Interest (SoI) drastically. In order to remove or reduce strong CW-NBI, various mitigation techniques have been proposed to mitigate CW and narrowband interference with communication signals such as prediction error filters [1-3], transform domain techniques [4-8], and adaptive notch filters [9-13]. The two approaches in narrowband interference suppression adaptive notch filters are classified into time-domain (TD) and frequency-domain (FD). In TD, papers [14-17] present methods for recovering a single-tone CW narrowband interference using an adaptive lattice IIR notch filter form. The linear prediction is considered as traditional time-domain filtering to remove the time-varying NBI [13]. In contrast, the nonlinear prediction methods considering the non-Gaussian environment [18-21] shown that the nonlinear prediction method achieves a higher SNR than the linear prediction method. The disadvantage of the conventional linear and nonlinear prediction filters requires longer tap filters to mitigate the effect of narrowband interference effectively, which increases the system’s complexity [14]. In FD, [22] proposed an N-sigma excision method to reject CWI. Also, FD and the space-time technique increase the hardware complexity and not suitable for mobile devices [23]. Paper [24] presents a comparative performance analysis of two adaptive notch filtering algorithms in GPS, But the disadvantage of this method the trade-off between the quality of interference removing and the computational complexity of the system. The ANF is useful for the detection and mitigation of jamming signals [25]. Paper [23] presents a novel algorithm for ANF based on direct IIR notch filter form structure, in contrast, the lattice form IIR notch filter provides better convergence properties, and more accurate frequency estimation compared to the direct form implementations [14,16,17]. The notch filter has proved to be an efficient mitigation technique for CW-NBI [15]. In literature, notch filters have been used for removing interference in different types of applications such as biomedical [26], GNSS applications, GPS receiver, and DSSS systems [14,15].IIR notch filter has constrained zeros on the unit circle, which makes the notch more “depth into infinite” that can remove the interference completely. But the disadvantage of this method creates self-noise caused by eliminating some of the useful signals at the notch frequency while removing the interference [14,16]. Self-noise is briefly described in [27]. To reduce the self-noise, Choi [14] proposed a Narrowband interference suppression technique using open-loop adaptive IIR notch filter in DSSS systems by controlling the depth of the notch according to the estimated JSR and CWI frequency. This will lead to maximizing the output SNR. However, in this paper, the approach is based on proposing a new LMS algorithm for mitigating CW narrowband interference in QPSK demodulation. This LMS algorithm is developed to obtain and then track the interference and adjust the depth of the notch according to the estimated JSR and CWI frequency.The rest of this paper is organized as follows. Section 2 describes the QPSK modulated baseband signal model in the presence of the CWI “system model,”. Whereas Section 3 describes and reviews the adaptive lattice IIR notch filter (ALNF), and proposing a new LMS algorithm for mitigating CW-NBI in QPSK demodulation. The optimal notch depth to maximize the output SNR of the notch filter is described in Section 4. Section 5 presents the simulation results and performance analysis. Finally, Section 6 concludes this paper.
2. QPSK Modulated Baseband Signal and Interference Signal, Models
- In this section, a QPSK modulated baseband signal and interference signal models are presented, as in Figure 1. A MATLAB simulation model is used to generate a QPSK signal and CW-NBI at different SNR and JSR.
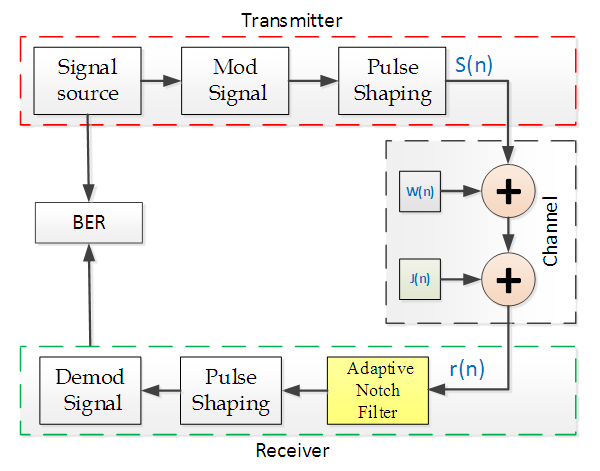 | Figure 1. Block Diagram of the System Model |
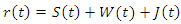 | (1) |
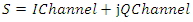 | (2) |
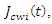 Can be modelled as given below [15].
Can be modelled as given below [15]. 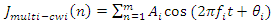 | (3) |
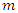 is the number of CWI and
is the number of CWI and 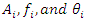 are the amplitudes, the frequencies, and the random phases uniformly distributed over
are the amplitudes, the frequencies, and the random phases uniformly distributed over 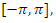 respectively. In this work, a case of a single interfering is considered and thus
respectively. In this work, a case of a single interfering is considered and thus  The received signal
The received signal  is then sampled and analog to digital converted, leading to
is then sampled and analog to digital converted, leading to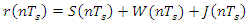 | (4) |
 will be ignored for ease of notation and the equation (4) will be adopted as given below
will be ignored for ease of notation and the equation (4) will be adopted as given below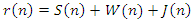 | (5) |
3. Review ALNF and Proposed LMS Algorithm for Mitigating CW-NBI
- In this section, the structures of the IIR notch filter is briefly presented. The adaptive IIR notch filter has been used and describes as Adaptive Line Enhancer (ALE) for enhancing the sinusoids corrupted by noise [16]. The IIR notch filter requires much less filter length than the Finite Impulse Response (FIR) and more widely used. Also, it can remove the interference signal or NBI efficiently [28]. The IIR notch filters can also obtain frequency response closer to ideal notch filter compared to FIR notch filters using the same length, [14]. The ANF is a common method used for estimating and tracking unknown frequencies of sinusoids degraded by noise. It has two main forms, direct and lattice forms [29]. In this paper, a system model consists of two adaptive lattice IIR notch filters, H1(z), and H2(z) for interference cancellation, which shown in Figure 2. In this system, assumed single-tone CWI and white Gaussian noise are added to QPSK modulated baseband signal as described in Eq.(5). In literature [14,16], the lattice IIR notch filter seems to have better performance than the direct IIR notch filter form. In general, the notch filter has proved to be an efficient mitigation technique for CW-NBI [15,30].
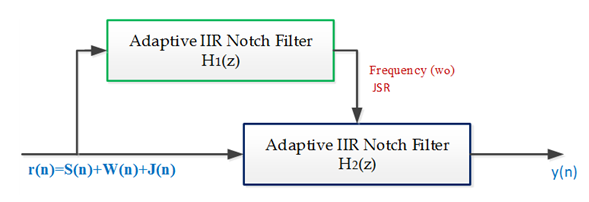 | Figure 2. System block diagram of the anti-jamming filter |
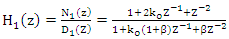 | (6) |
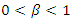 is the pole-zero contraction factor that adjusts the width of the notch.
is the pole-zero contraction factor that adjusts the width of the notch. 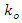 is related to the notch frequency that decides to reject the CWI, and
is related to the notch frequency that decides to reject the CWI, and 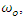 is defined as
is defined as 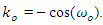 The transfer function of
The transfer function of 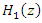 consists of two parts, the auto-regression (AR) block and the moving average (MA) block, which described in Figure 3. The MA block can remove the signal on the interference center frequency as well as the signal located near the interference frequency where the transmitted data are located. Thus, as AR and MA blocks are used simultaneously, the filter can reject only the interference frequency signal so that they reduce the information signal loss [15].
consists of two parts, the auto-regression (AR) block and the moving average (MA) block, which described in Figure 3. The MA block can remove the signal on the interference center frequency as well as the signal located near the interference frequency where the transmitted data are located. Thus, as AR and MA blocks are used simultaneously, the filter can reject only the interference frequency signal so that they reduce the information signal loss [15]. 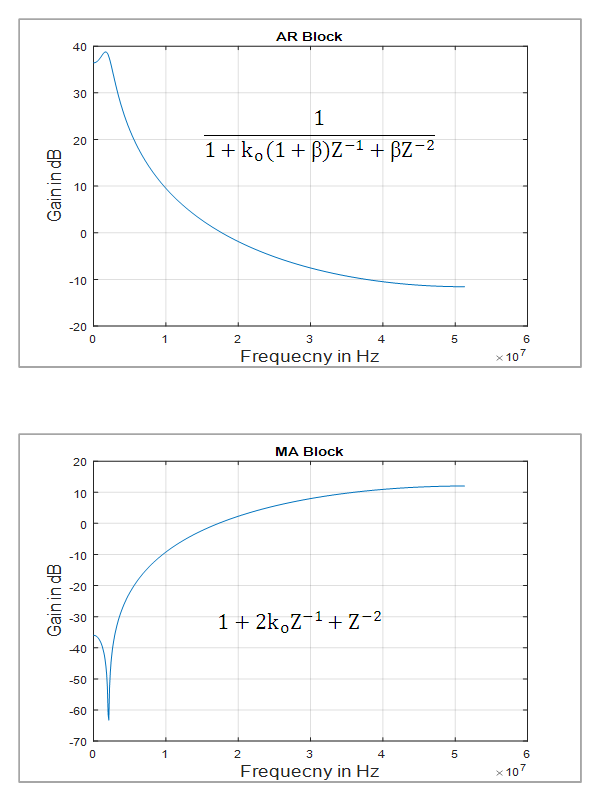 | Figure 3. Adaptive IIR notch filter structure |
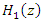 has one notch frequency and zero on the unit circle, which resulting in-depth into infinite.By taking the inverse Z-transform of
has one notch frequency and zero on the unit circle, which resulting in-depth into infinite.By taking the inverse Z-transform of 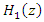 , it is accessible to an illustration that the filter output can be expressed as given by:
, it is accessible to an illustration that the filter output can be expressed as given by: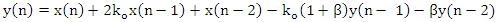 | (7) |
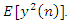 In this work, equation (12) is the developed LMS algorithm for the proposed adaptive notch filter, which based on the gradient-based method of steepest descent. As we are trying to minimize the mean-squared output energy level
In this work, equation (12) is the developed LMS algorithm for the proposed adaptive notch filter, which based on the gradient-based method of steepest descent. As we are trying to minimize the mean-squared output energy level 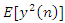 instead of minimizing the mean-squared error MSE which is given by
instead of minimizing the mean-squared error MSE which is given by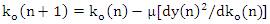 | (8) |
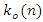
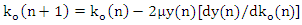 | (9) |
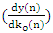 can be derived as
can be derived as 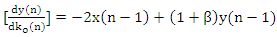 | (10) |
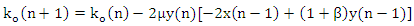 | (11) |
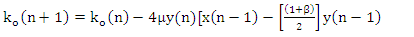 | (12) |
 and
and 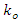 are related by
are related by 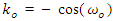 where
where 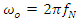 , then the estimated frequency at sample n is given by
, then the estimated frequency at sample n is given by 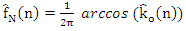 | (13) |
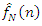 is used to place notch by calculating
is used to place notch by calculating 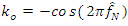 . Also, using
. Also, using 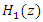 to estimate JSR, by subtracting the output of the notch filter from the received signal as is given by
to estimate JSR, by subtracting the output of the notch filter from the received signal as is given by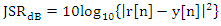 | (14) |
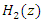 to control
to control 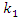 based on the estimation of JSR by
based on the estimation of JSR by 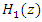 to maximize the output SNR at
to maximize the output SNR at 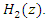 The transfer function of the lattice notch filter
The transfer function of the lattice notch filter 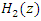 [14] is given by
[14] is given by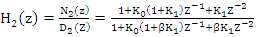 | (15) |
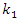 is controlling the depth of the notch filter and depends on the estimated JSR by
is controlling the depth of the notch filter and depends on the estimated JSR by 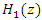 and
and 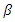 is controlling the width of the notch filter. There are many implementation schemes for obtaining
is controlling the width of the notch filter. There are many implementation schemes for obtaining 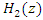 . But this work implement
. But this work implement 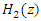 [14] by cascading all-pole and all zero lattice IIR filter, as shown in Figure 4. If we set
[14] by cascading all-pole and all zero lattice IIR filter, as shown in Figure 4. If we set 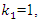 the result of the transfer function
the result of the transfer function 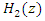 will be the same as the transfer function
will be the same as the transfer function 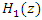 , which has zero on the unit circle hence resulting in-depth into infinite of the notch that can remove the interference completely. As stated previously, with infinite depth of the notch filter, the interference is removed completely, but it creates self-noise at the notch filter caused by eliminating some of the useful signals. Hence, the depth of the notch
, which has zero on the unit circle hence resulting in-depth into infinite of the notch that can remove the interference completely. As stated previously, with infinite depth of the notch filter, the interference is removed completely, but it creates self-noise at the notch filter caused by eliminating some of the useful signals. Hence, the depth of the notch 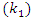 should be adjusted with the interference power. Therefore, the IIR notch filter
should be adjusted with the interference power. Therefore, the IIR notch filter 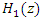 and
and 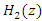 can be performed using the same structure, and the notch of Eq.(15) can be placed on the IF by copying
can be performed using the same structure, and the notch of Eq.(15) can be placed on the IF by copying 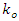 of the IIR notch filter
of the IIR notch filter 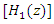 that is tuned to IF by Eq.(12).
that is tuned to IF by Eq.(12).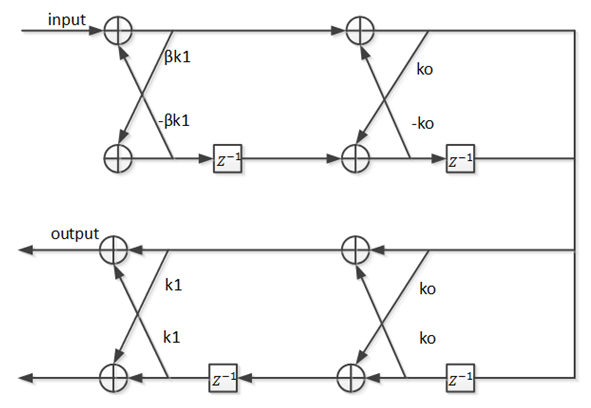 | Figure 4. The lattice IIR notch filter structuration |
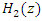 can be expressed as
can be expressed as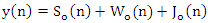 | (16) |
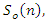
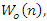 and
and 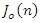 are the output components of the desired QPSK modulated baseband signal, white Gaussian noise, and CW narrowband interference, respectively.Figure 5 and Figure 6 show the power spectrum of the received signal before and after filtering. From these figures, with infinite depth of the notch filter, the interference is removed completely, but some of the useful signals are also removed while removing the interference. Hence, in order to minimize loss of the useful signal, the depth of the notch
are the output components of the desired QPSK modulated baseband signal, white Gaussian noise, and CW narrowband interference, respectively.Figure 5 and Figure 6 show the power spectrum of the received signal before and after filtering. From these figures, with infinite depth of the notch filter, the interference is removed completely, but some of the useful signals are also removed while removing the interference. Hence, in order to minimize loss of the useful signal, the depth of the notch 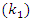 should be adjusted, which described in the section (4).
should be adjusted, which described in the section (4).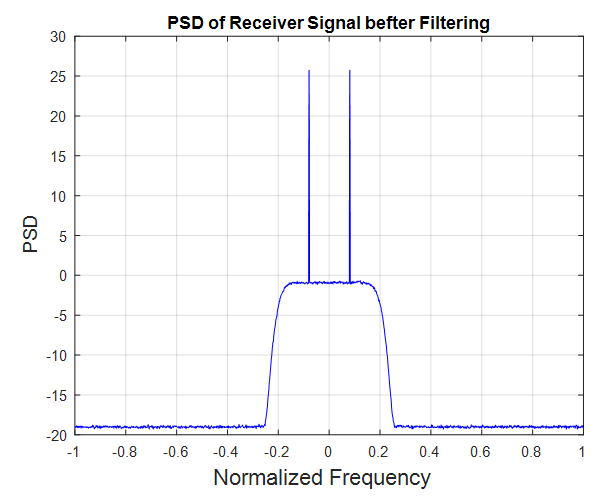 | Figure 5. The power spectrum of received signal before filtering |
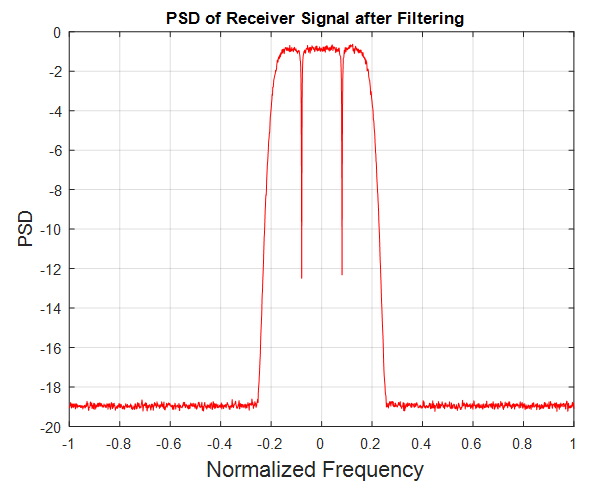 | Figure 6. The power spectrum of the received signal after filtering |
4. Optimal Value of the Notch Depth to Maximize the Output SNR
- Papers [1,8] expressed the output SNR of the notch filter as a function of parameters as given by
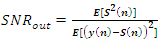 | (17) |
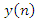 is the output of the IIR notch filter
is the output of the IIR notch filter 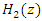 . The
. The 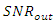 finally can be expressed in terms of the filter parameters as [14], given by Eq.(18).
finally can be expressed in terms of the filter parameters as [14], given by Eq.(18).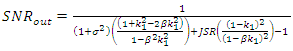 | (18) |
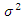 is the AWGN variance and JSR equals
is the AWGN variance and JSR equals 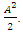 Assuming the first part of equation (18) is equal to D, as shown in equation (19), which called self-noise of the notch.
Assuming the first part of equation (18) is equal to D, as shown in equation (19), which called self-noise of the notch.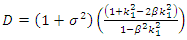 | (19) |
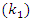 increases, D shows a large value. In order to maximize SNR output, the optimal
increases, D shows a large value. In order to maximize SNR output, the optimal 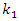 need to be found to minimizes denominator in equation (18) with a fixed value of
need to be found to minimizes denominator in equation (18) with a fixed value of 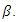 The denominator in equation (18) can be expressed as a function of the depth of the notch
The denominator in equation (18) can be expressed as a function of the depth of the notch 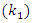 after some modification.
after some modification.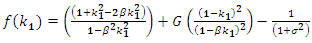 | (20) |
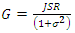 . To find the optimal
. To find the optimal 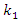 , we differentiate
, we differentiate 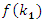 and solve
and solve 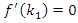 for all possible roots of
for all possible roots of 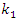 as
as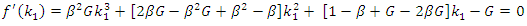 | (21) |
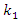 as a function of JSR.
as a function of JSR.5. Simulation Results and Performance Analysis
- In this section, the simulated performance of the proposed system is investigated in terms of the SNR output of the notch filter for varying JSR and the SOI power
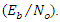 A single tone CWI of 0.04 rad center frequency is considered in this work. However, it can be any value in the range of [0-1]. The simulations are run for 1e6 data bits, for the narrowband interference, β is chosen to be 0.98, which gives more satisfying results for various situations. Large β is known to give more accurate estimates of JSR and frequency from the notch filter (H1z), but slower convergence and tracking [16].Figure 7 and Figure 8 show the estimated optimal value of k1 as a function of JSR, with different
A single tone CWI of 0.04 rad center frequency is considered in this work. However, it can be any value in the range of [0-1]. The simulations are run for 1e6 data bits, for the narrowband interference, β is chosen to be 0.98, which gives more satisfying results for various situations. Large β is known to give more accurate estimates of JSR and frequency from the notch filter (H1z), but slower convergence and tracking [16].Figure 7 and Figure 8 show the estimated optimal value of k1 as a function of JSR, with different 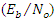 power and a fixed width of the notch filter “β.” From this figure, the k1 approaches 1 as the JSR increases. In addition, the result shows that the increasing of JSR to approach k1=1 also depend on
power and a fixed width of the notch filter “β.” From this figure, the k1 approaches 1 as the JSR increases. In addition, the result shows that the increasing of JSR to approach k1=1 also depend on 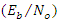 power and β, so as
power and β, so as 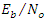 and β decreased, the JSR increasing to approaches k1=1.
and β decreased, the JSR increasing to approaches k1=1.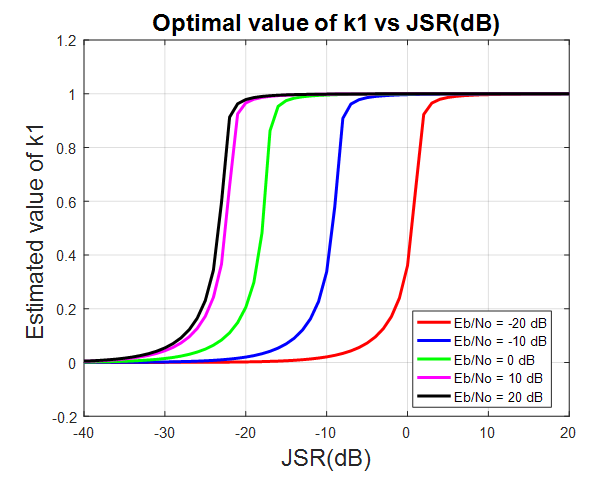 | Figure 7. Optimal value of k1 vs. JSR with 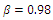 |
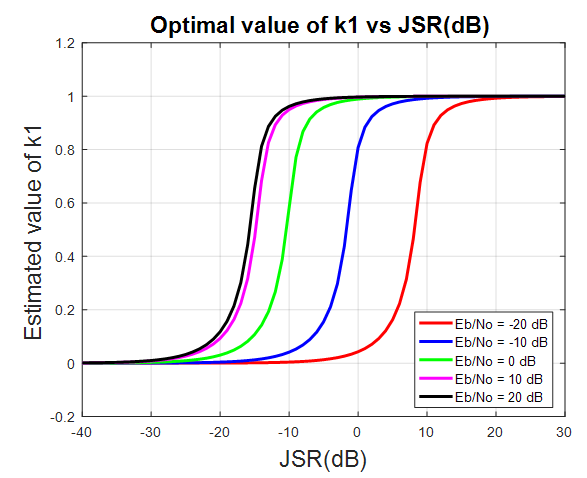 | Figure 8. Optimal value of k1 vs. JSR with 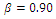 |
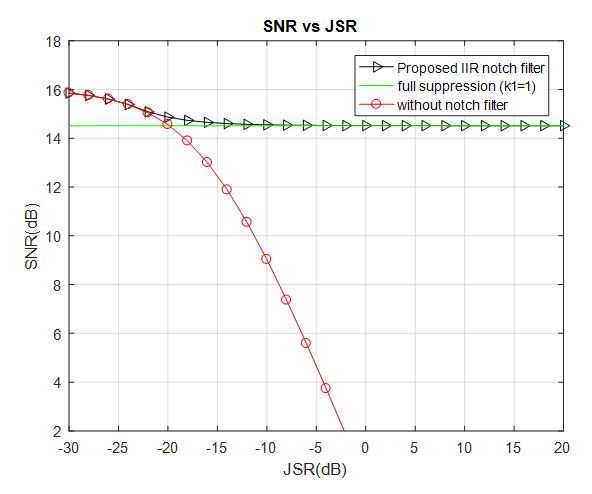 | Figure 9. SNR vs. JSR with 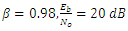 |
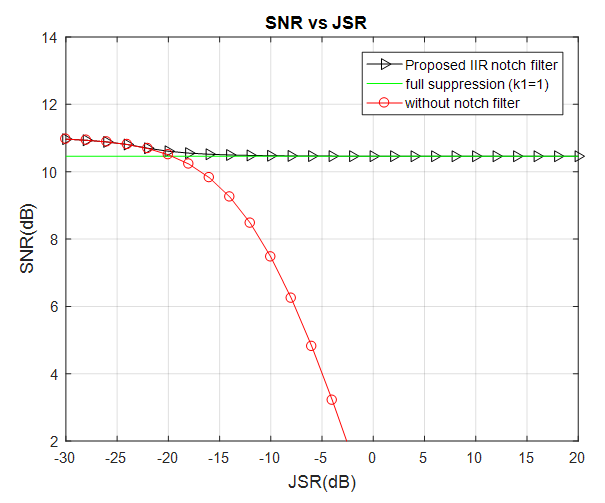 | Figure 10. SNR vs. JSR with 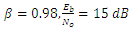 |
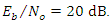
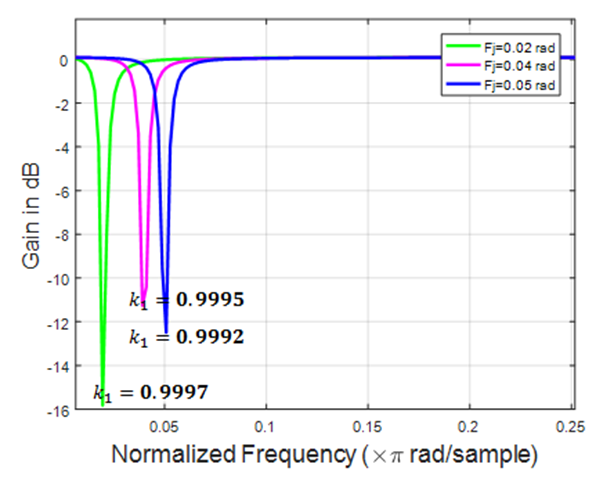 | Figure 11. Depth of the notch with estimated JSR |
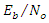 power (15 dB and 20 dB). The result shows the compared with the Proposed IIR notch filter algorithm and without notch filter “no filtering.”
power (15 dB and 20 dB). The result shows the compared with the Proposed IIR notch filter algorithm and without notch filter “no filtering.”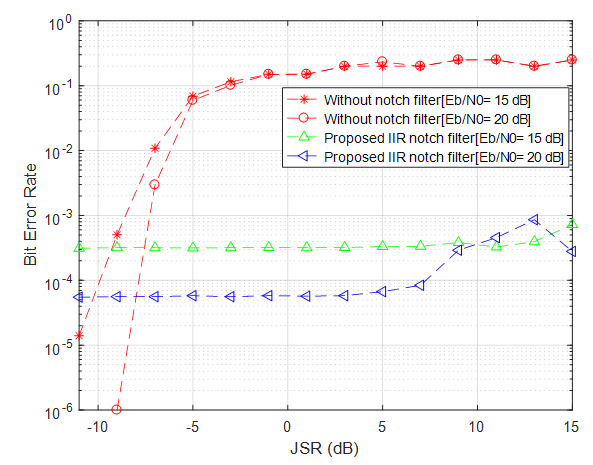 | Figure 12. BER vs. JSR with 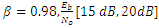 |
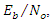 when the simulations run as
when the simulations run as 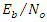 values changes (-20 dB to 10 dB) and with a fixed values of Jamming power (15 dB and 20 dB).
values changes (-20 dB to 10 dB) and with a fixed values of Jamming power (15 dB and 20 dB). | Figure 13. BER vs 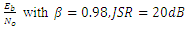 |
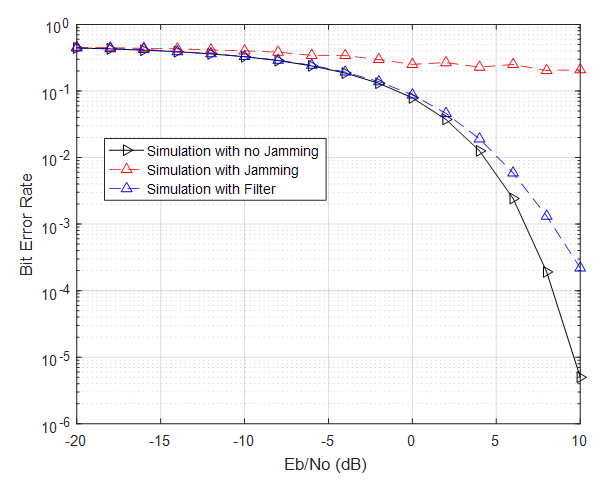 | Figure 14. BER vs 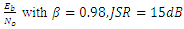 |
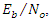 when the simulations run as Eb/No values changes (-20 dB to 10 dB) and a fixed value of Jamming power (20 dB and 15 dB) with estimated the depth of the notch
when the simulations run as Eb/No values changes (-20 dB to 10 dB) and a fixed value of Jamming power (20 dB and 15 dB) with estimated the depth of the notch 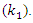
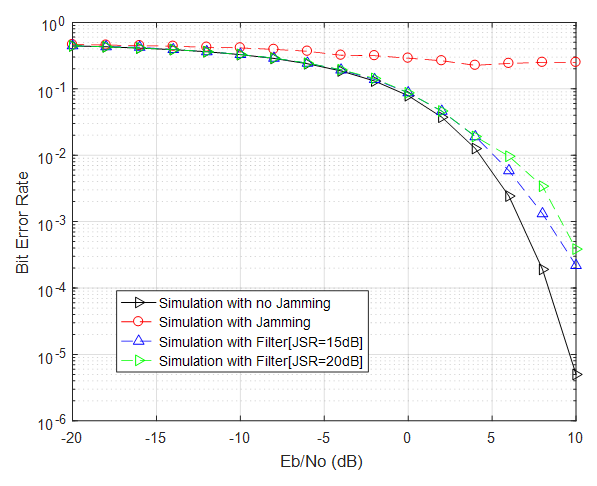 | Figure 15. BER vs 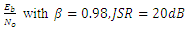 |
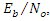 when JSR = 15 dB. From this figure, the simulation with no jamming is matched the theoretical.
when JSR = 15 dB. From this figure, the simulation with no jamming is matched the theoretical.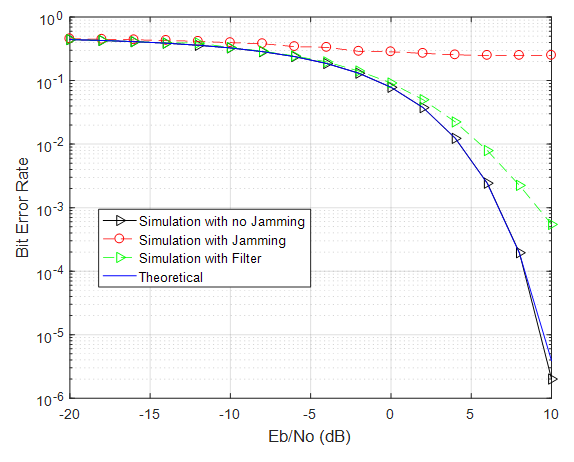 | Figure 16. BER vs 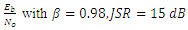 |
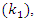 the interference is removed according to the estimated JSR.
the interference is removed according to the estimated JSR.  | Figure 17. Input and output PSD of the notch filter with, 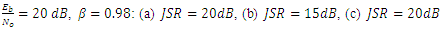 |
6. Conclusions
- This paper proposed an IIR notch filter that improved the performance of the system for CW-NBI suppression. The filter comprises two ANF structures and an LMS algorithm working in parallel. The first IIR notch filter detects the interference in the received signal, and then the second IIR notch filter removes the interference and adjusts the depth of the notch according to the estimated power of the interference. The notch becomes deeper for higher JSR to reduce the effect of stronger interference while becomes smaller for a lower value of JSR. Thus, as a conclusion, the proposed IIR notch filter can effectively detect CW-NBI and adjust the depth of the notch for any given value of JSR and provides better BER performance. Also, it maximizes the SNR output of notch filter for lower and higher values of JSR with different values of
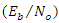 power. Therefore, this technique can be applied in a DVB-S2 receiver or any other communication and navigation receivers.
power. Therefore, this technique can be applied in a DVB-S2 receiver or any other communication and navigation receivers.ACKNOWLEDGEMENTS
- The work reported in this paper was done under AVIO 601 - Interference Mitigation in Satellite Communication, project of LASSENA, ÉTS.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML