Er'el Granot
Department of Electrical and Electronics Engineering, Ariel University, Ariel, Israel
Correspondence to: Er'el Granot, Department of Electrical and Electronics Engineering, Ariel University, Ariel, Israel.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
There are multiply approaches to prove Euler's well-known formula, however, none of them is trivial or simple. In this paper we utilize Nyquist-Shannon sampling theorem to prove Euler's formula in particular and Riemann's 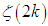 in general in a straightforward approach. The presented method allows calculating the summation of several other similar series, such as
in general in a straightforward approach. The presented method allows calculating the summation of several other similar series, such as 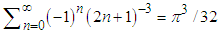 , and even more surprising ones such as
, and even more surprising ones such as 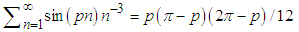 .
.
Keywords:
Euler's theorem, Sampling theorem, Riemann's zeta function, Basel problem, Nyquist-Shannon theorem
Cite this paper: Er'el Granot, Derivation of Euler's Formula and ζ(2k) Using the Nyquist-Shannon Sampling Theorem, American Journal of Signal Processing, Vol. 9 No. 1, 2019, pp. 1-5. doi: 10.5923/j.ajsp.20190901.01.
1. Introduction
Euler is definitely one of the greatest mathematicians of all times. His contribution to science is incredible by any measure or standard. However, his first contribution that made him famous by the age of twenty eight was the identity, which is called after him. We are not referring to the well-known identity 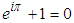 , which is erroneously called Euler’s identity, for it should have been related to Cotes, who presented it many years prior to Euler. The real Euler’s identity was the solution of, what was termed the Basel problem, which was first presented in 1644 by Pietro Mengoli and later by the Bernoulli brothers, who could not solve the problem. The problem was to calculate the sum of the infinite series (also known as Riemann's
, which is erroneously called Euler’s identity, for it should have been related to Cotes, who presented it many years prior to Euler. The real Euler’s identity was the solution of, what was termed the Basel problem, which was first presented in 1644 by Pietro Mengoli and later by the Bernoulli brothers, who could not solve the problem. The problem was to calculate the sum of the infinite series (also known as Riemann's 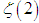 )
)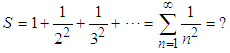 | (1) |
Euler first presented an advanced numerical method to calculate the sum, which he later used to validate the exact closed-form solution, which came later on. Euler proved that this series sums to 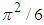 [1]. After the publications of the first proof, many equivalent proofs followed, which illustrates the fact that this identity appears in many places in mathematics and science [2-15].One can find proofs that are based on multiple integrals, trigonometric identities, inverse trigonometric functions, complex analysis, Fourier analysis, and even geometric reasoning, however, there is none, to the best my knowledge, which is based on Signal Processing's Sampling theorem. The objective of this paper is to show that with the aid of Digital Signal Processing (DSP) analysis, using the Sampling theorem, the proof of this mathematical identity becomes almost straightforward.For completeness, we will remind the reader of the Sampling theorem and present the original Euler’s derivation.The Nyquist- Shannon Sampling Theorem: If an analog signal
[1]. After the publications of the first proof, many equivalent proofs followed, which illustrates the fact that this identity appears in many places in mathematics and science [2-15].One can find proofs that are based on multiple integrals, trigonometric identities, inverse trigonometric functions, complex analysis, Fourier analysis, and even geometric reasoning, however, there is none, to the best my knowledge, which is based on Signal Processing's Sampling theorem. The objective of this paper is to show that with the aid of Digital Signal Processing (DSP) analysis, using the Sampling theorem, the proof of this mathematical identity becomes almost straightforward.For completeness, we will remind the reader of the Sampling theorem and present the original Euler’s derivation.The Nyquist- Shannon Sampling Theorem: If an analog signal 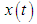 is sampled at a rate
is sampled at a rate 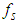 (which means that only
(which means that only 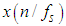 are known), then the original signal can be exactly recovered from its sample values
are known), then the original signal can be exactly recovered from its sample values 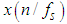 by the discrete convolution
by the discrete convolution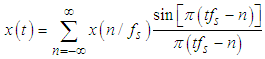 provided
provided 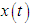 is spectrally bounded by the frequency
is spectrally bounded by the frequency 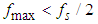 .Euler's Derivation: Euler used the Taylor expansion of the sinc function [16]
.Euler's Derivation: Euler used the Taylor expansion of the sinc function [16]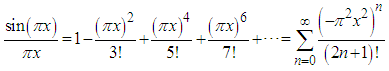 | (2) |
Then, Euler made a brilliant idea, which took him about a decade to prove in a more rigorous method, and in fact, it took about an additional century to cement the idea with Weierstrass factorization theorem [17].Euler idea was to implement Newton factorization method to infinite products, i.e., it was shown by Newton that any polynomial can be rewritten as a product of linear factors, which vanish at its roots [18]. Euler idea was to generalize it even to cases where the number of roots is infinite. Since the sinc function vanishes for 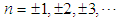 then Euler assumed, but he had difficulties in proving, that
then Euler assumed, but he had difficulties in proving, that 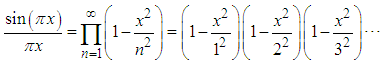 | (3) |
Now, after opening all brackets and collecting all terms, 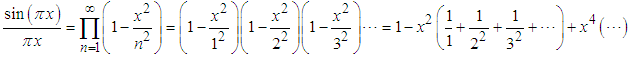 | (4) |
That is, the coefficient of 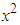 is the infinite series
is the infinite series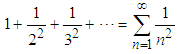 | (5) |
However, from (2) it is clear that the coefficient of 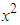 is
is 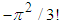 , therefore
, therefore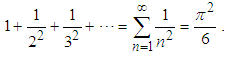 | (6) |
In the literature In what follows we will show that this relation can be retrieved easily using Digital Signal Processing analysis. Moreover, it will be shown that the derivation is almost straightforward.
2. The Sampling Theorem Approach
It is well-known that any spectrally bounded signal can be written as a superposition of delayed sinc functions [19, 20]. In particular (see Fig.1),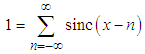 | (7) |
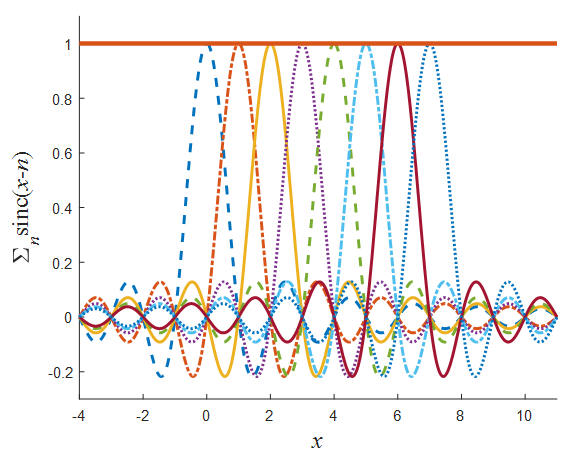 | Figure 1. Illustration of Eq.(7). "1" can be rewritten as an infinite sum of "sinc" pulses (in the figure only eight are presented) |
There are many ways to prove this identity, one of which is to use Nyquist- Shannon(NS) theorem (mostly known as the "sampling theorem", see above) [19, 20], which shows that since the constant "1" (left side of Eq.(1)) has a zero bandwidth, then if this identity is valid for any 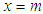 , where
, where 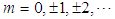 then it is valid for any x. Another option is to recognize the fact that the Fourier transform of both sides of the equation are equal to the delta function, i.e.
then it is valid for any x. Another option is to recognize the fact that the Fourier transform of both sides of the equation are equal to the delta function, i.e.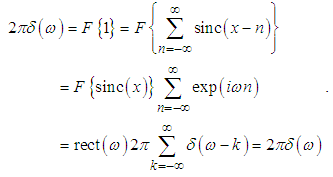 | (8) |
Since Eq.(7) is valid for any x, then clearly all its derivatives must vanishes. In particular, the second derivative must vanish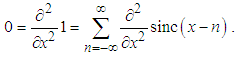 | (9) |
Now since,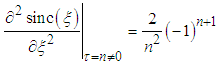 | (10) |
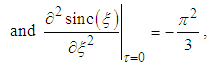 | (11) |
then the second derivative at any integer 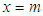 must be equal to
must be equal to | (12) |
This is the first identity, but it is not Euler's formula yet. However, it is very simple to show that Eq.(12) is exactly half Eq.(5) since | (13) |
Thus, Eq.(6) is retrieved. Similarly, by taking the 4th derivative of Eq.(7) and using | (14) |
One finds | (15) |
which yields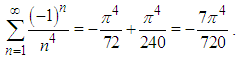 | (16) |
Now since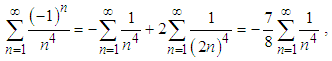 | (17) |
then, finally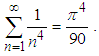 | (18) |
Clearly, this method can be used to derive any summation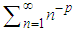 for any even integer p, i.e., it can be used to calculate Riemann's
for any even integer p, i.e., it can be used to calculate Riemann's 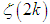 for any integer k.However, one can use even a simpler approach for this problem:Eq.(7) is actually
for any integer k.However, one can use even a simpler approach for this problem:Eq.(7) is actually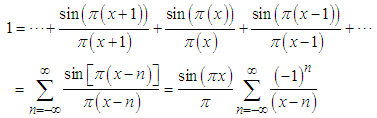 | (19) |
Therefore, Eq.(7) can be rewritten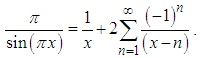 | (20) |
Then, by applying the Lauren expansion on the two sides of the equation, one obtains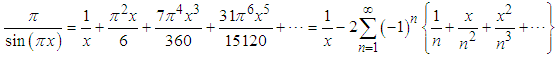 | (21) |
By comparing the coefficient of x Eq.(12) appears, and by comparing the coefficient of 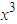 Eq.(16) appears.The same approach can be applied to other spectrally bounded functions, such as (see Fig.2)
Eq.(16) appears.The same approach can be applied to other spectrally bounded functions, such as (see Fig.2)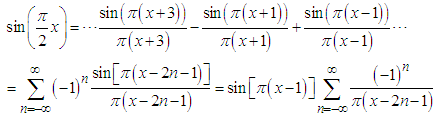 | (22) |
which is equivalent to 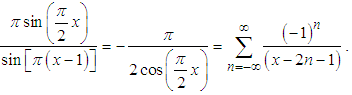 | (23) |
Again, Eq.(22) agrees with the Sampling theorem since the spectrum of 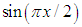 is bounded within the spectral regime
is bounded within the spectral regime 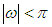 .
.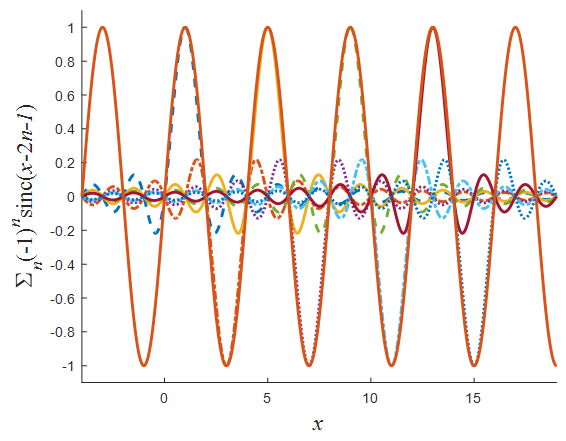 | Figure 2. Illustration of Eq.(22). 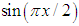 (solid curve) can be rewritten as an infinite sum of "sinc" pulses with alternating signs (in the figure only eight are presented) (solid curve) can be rewritten as an infinite sum of "sinc" pulses with alternating signs (in the figure only eight are presented) |
Again, one can expand the two sides of the equation to get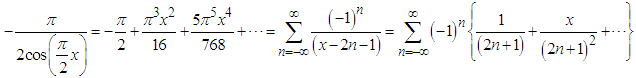 | (24) |
By comparing the coefficient of the 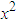 term on both sides of Eq.(24) one gets
term on both sides of Eq.(24) one gets 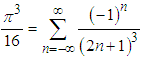 | (25) |
and by comparing the 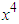 coefficients
coefficients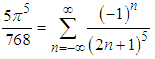 | (26) |
(Clearly, the odd terms vanish). Therefore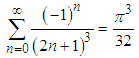 | (27) |
and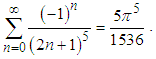 | (28) |
Clearly, this method can be applied to calculate the generic summation 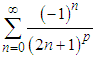 for any odd
for any odd 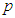 .
.
3. Generalization
One can use the original NS sampling theorem 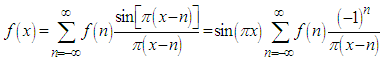 | (29) |
for any function  , whose spectrum, i.e. its Fourier transform is spectrally bounded in
, whose spectrum, i.e. its Fourier transform is spectrally bounded in  , to derive a generic relation
, to derive a generic relation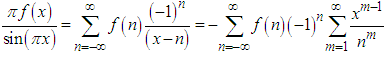 | (30) |
where the last equality is simply the Taylor expansion of the former.By comparing the coefficients of 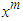
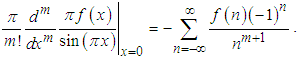 | (31) |
In particular, if 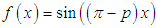 for
for 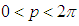 then
then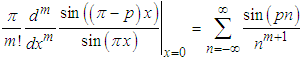 | (32) |
and therefore for even m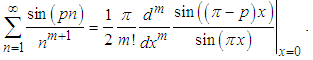 | (33) |
For example, for 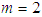 (see Fig.3)
(see Fig.3)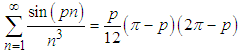 | (34) |
for 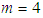
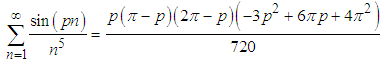 | (35) |
for 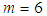
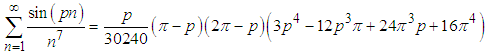 | (36) |
etc.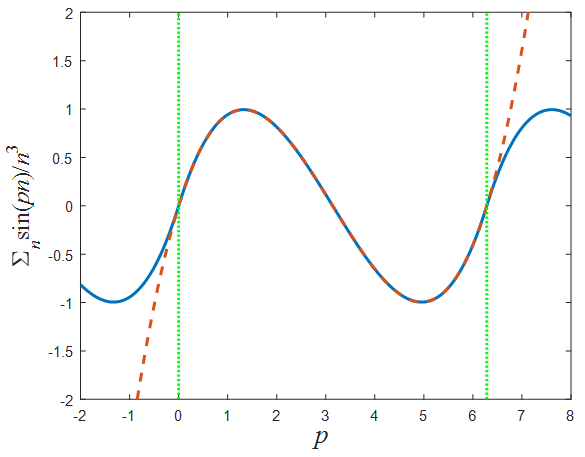 | Figure 3. Illustration of Eq.(34). The solid curve represents the left side of the equation, while the dashed curve represents its right side. As can be seen the two agree provided 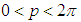 (confined by the vertical dotted lines) (confined by the vertical dotted lines) |
Note, that when Eq.(34) is divided by p and then the limit 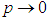 is taken, the original Euler formula, i.e. Eq.(6), is retrieved
is taken, the original Euler formula, i.e. Eq.(6), is retrieved 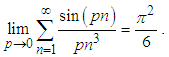 Similarly, when
Similarly, when 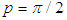 then Eq.(34) reduces to Eq.(27).
then Eq.(34) reduces to Eq.(27).
4. Conclusions and Summary
The Sampling theorem, which is one of the cornerstones of Digital Signal Processing, can be utilized to prove Euler's formula in a straightforward approach. In fact, it is a straightforward consequence of the fact that an infinite sum of sinc functions is equal to 1. This identity, which is a consequence of the sampling theorem, cannot be valid unless Euler's formula is. Moreover, by applying this theorem to harmonic functions, an abundance of mathematical relations appear. In particular, any of the following summations has a simple analytical solution, which can be written as a polynomial: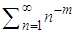 for any even number m,
for any even number m, 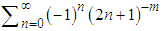 for any odd number m,
for any odd number m, 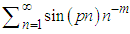 for any odd number m,
for any odd number m, 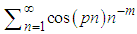 for any even number mand others.Thus, this paper illustrates the strength of the Sampling Theorem to derive the summation of infinite series.
for any even number mand others.Thus, this paper illustrates the strength of the Sampling Theorem to derive the summation of infinite series.
References
| [1] | R. Ayoub, "Euler and the zeta function". Amer. Math. Monthly. 81, 1067–86 (1974). |
| [2] | J. Breckling, R. Chapman, "Evaluating ζ(2) " available online: http://empslocal.ex.ac.uk/people/staff/rjchapma/etc/zeta2.pdf. |
| [3] | E.W. Weisstein, "Riemann Zeta Function ζ(2)". MathWorld. Retrieved 29 April 2018. |
| [4] | E. de Amo, M. D. Carrillo, and J. Fernández-Sánchez, "Another Proof of Euler's Formula for ζ(2k)", Proc. Of the Am. Mathema. Soc., 139, 1441–1444 (2011). |
| [5] | M. Wegmuller, J. P. von der Weid, P. Oberson, and N. Gisin, “High resolution fiber distributed measurements with coherent OFDR,” in Proc. ECOC’00, 2000, paper 11.3.4, p. 109. |
| [6] | R. For a nice geometric proof, see "Why is pi here? And why is it squared? A geometric answer to the Basel problem": 3 Blue 1 Brown (2018) available online: https://www.youtube.com/watch?v=d-o3eB9sfls. |
| [7] | Apostol, Tom M., A proof that Euler missed: evaluating ζ(2) the easy way, Math. Intelligencer 5, 59–60 (1983). |
| [8] | Lord, Nick, Yet another proof that ζ(2)=π2/6, Math. Gaz. 86, 477–479 (2002). |
| [9] | B. R. Choe, "An Elementary Proof of ζ(2)=π2/6", The American Mathematical Monthly, 94, 662-663 (1987). |
| [10] | T. M. Apostol, "Mathematical Analysis" 2nd ed. (Addison-Wesley, 1974). |
| [11] | R. A. Kortram, "Simple proof for Σkk-2=π2/6 and sin(x)=xΠk(1-x2/k2π2)" Mathematics Magazine, 69, 122-125 (1996). |
| [12] | Yoshio Matsuoka, "An elementary proof of the formula Σkk-2= π2/6", The American Mathematical Monthly, 68, 485-487 (1961). |
| [13] | E. L. Stark, "Another Proof of the Formula ∑ 1/k2 = π2/6" The American Mathematical Monthly, 76, 552-553 (1969). |
| [14] | J.M. Borwein and P.B. Borwein, " Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity", Wiley 1987. |
| [15] | L.K. Hua, "Introduction to Number Theory" Springer-Verlag Berlin Heidelberg 1982. |
| [16] | Hazewinkel, Michiel, ed., "Taylor series", Encyclopedia of Mathematics, Springer (2001). |
| [17] | Krantz, S. G., "Weierstrass's Theorem" §8.3.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 111, 1999. |
| [18] | Knopp, K., "Weierstrass's Factor-Theorem", Theory of Functions, Part II, New York: Dover, pp. 1–7 (1996). |
| [19] | J.G. Proakis and D.G. Manolakis, Digital Signal Processing, (Prentice Hall, New-Jersey 1996). |
| [20] | A.V. Oppenheim and R. W. Schafer, "Discrete-Time Signal Processing", Prentice-Hall 1999. |



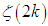 in general in a straightforward approach. The presented method allows calculating the summation of several other similar series, such as
in general in a straightforward approach. The presented method allows calculating the summation of several other similar series, such as 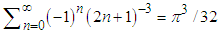 , and even more surprising ones such as
, and even more surprising ones such as 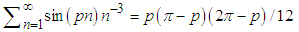 .
.
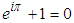 , which is erroneously called Euler’s identity, for it should have been related to Cotes, who presented it many years prior to Euler. The real Euler’s identity was the solution of, what was termed the Basel problem, which was first presented in 1644 by Pietro Mengoli and later by the Bernoulli brothers, who could not solve the problem. The problem was to calculate the sum of the infinite series (also known as Riemann's
, which is erroneously called Euler’s identity, for it should have been related to Cotes, who presented it many years prior to Euler. The real Euler’s identity was the solution of, what was termed the Basel problem, which was first presented in 1644 by Pietro Mengoli and later by the Bernoulli brothers, who could not solve the problem. The problem was to calculate the sum of the infinite series (also known as Riemann's 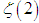 )
)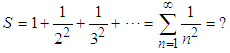
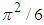 [1]. After the publications of the first proof, many equivalent proofs followed, which illustrates the fact that this identity appears in many places in mathematics and science [2-15].One can find proofs that are based on multiple integrals, trigonometric identities, inverse trigonometric functions, complex analysis, Fourier analysis, and even geometric reasoning, however, there is none, to the best my knowledge, which is based on Signal Processing's Sampling theorem. The objective of this paper is to show that with the aid of Digital Signal Processing (DSP) analysis, using the Sampling theorem, the proof of this mathematical identity becomes almost straightforward.For completeness, we will remind the reader of the Sampling theorem and present the original Euler’s derivation.The Nyquist- Shannon Sampling Theorem: If an analog signal
[1]. After the publications of the first proof, many equivalent proofs followed, which illustrates the fact that this identity appears in many places in mathematics and science [2-15].One can find proofs that are based on multiple integrals, trigonometric identities, inverse trigonometric functions, complex analysis, Fourier analysis, and even geometric reasoning, however, there is none, to the best my knowledge, which is based on Signal Processing's Sampling theorem. The objective of this paper is to show that with the aid of Digital Signal Processing (DSP) analysis, using the Sampling theorem, the proof of this mathematical identity becomes almost straightforward.For completeness, we will remind the reader of the Sampling theorem and present the original Euler’s derivation.The Nyquist- Shannon Sampling Theorem: If an analog signal 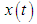 is sampled at a rate
is sampled at a rate 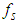 (which means that only
(which means that only 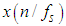 are known), then the original signal can be exactly recovered from its sample values
are known), then the original signal can be exactly recovered from its sample values 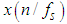 by the discrete convolution
by the discrete convolution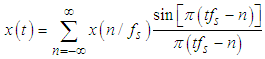 provided
provided  is spectrally bounded by the frequency
is spectrally bounded by the frequency  .Euler's Derivation: Euler used the Taylor expansion of the sinc function [16]
.Euler's Derivation: Euler used the Taylor expansion of the sinc function [16]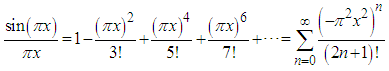
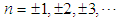 then Euler assumed, but he had difficulties in proving, that
then Euler assumed, but he had difficulties in proving, that 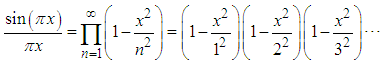
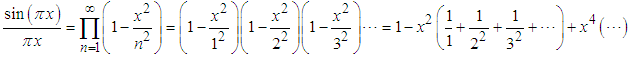
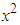 is the infinite series
is the infinite series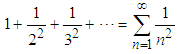
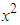 is
is 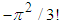 , therefore
, therefore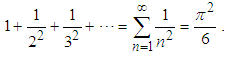
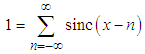

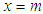 , where
, where 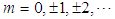 then it is valid for any x. Another option is to recognize the fact that the Fourier transform of both sides of the equation are equal to the delta function, i.e.
then it is valid for any x. Another option is to recognize the fact that the Fourier transform of both sides of the equation are equal to the delta function, i.e.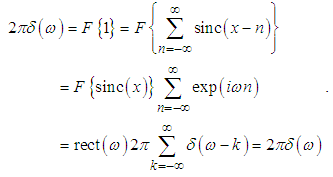
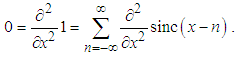
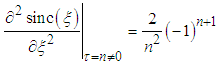
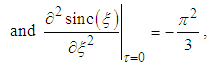
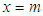 must be equal to
must be equal to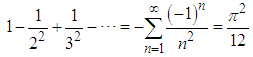
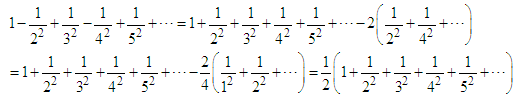
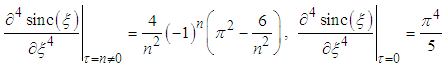
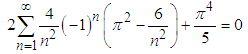
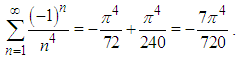
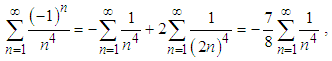
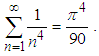
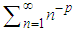 for any even integer p, i.e., it can be used to calculate Riemann's
for any even integer p, i.e., it can be used to calculate Riemann's 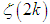 for any integer k.However, one can use even a simpler approach for this problem:Eq.(7) is actually
for any integer k.However, one can use even a simpler approach for this problem:Eq.(7) is actually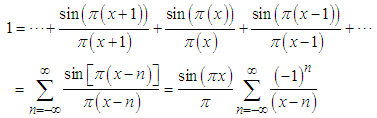
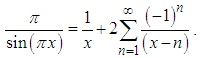
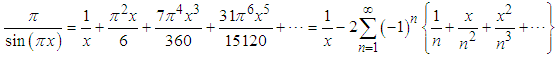
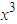 Eq.(16) appears.The same approach can be applied to other spectrally bounded functions, such as (see Fig.2)
Eq.(16) appears.The same approach can be applied to other spectrally bounded functions, such as (see Fig.2)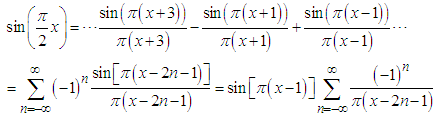
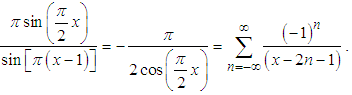
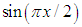 is bounded within the spectral regime
is bounded within the spectral regime 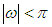 .
.
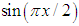 (solid curve) can be rewritten as an infinite sum of "sinc" pulses with alternating signs (in the figure only eight are presented)
(solid curve) can be rewritten as an infinite sum of "sinc" pulses with alternating signs (in the figure only eight are presented)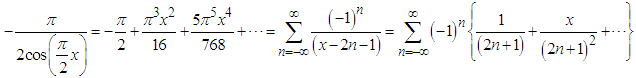
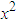 term on both sides of Eq.(24) one gets
term on both sides of Eq.(24) one gets 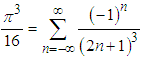
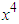 coefficients
coefficients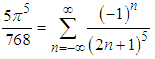
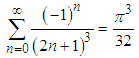
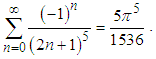
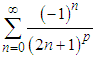 for any odd
for any odd 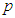 .
.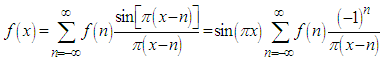
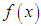 , whose spectrum, i.e. its Fourier transform is spectrally bounded in
, whose spectrum, i.e. its Fourier transform is spectrally bounded in 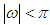 , to derive a generic relation
, to derive a generic relation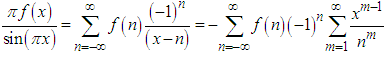
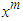
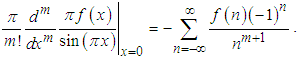
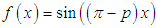 for
for 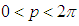 then
then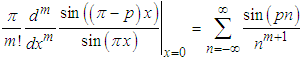
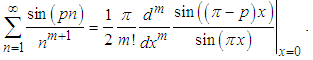
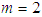 (see Fig.3)
(see Fig.3)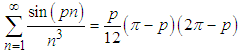
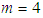
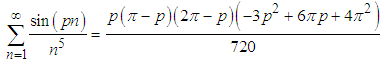
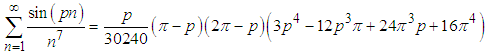
 is taken, the original Euler formula, i.e. Eq.(6), is retrieved
is taken, the original Euler formula, i.e. Eq.(6), is retrieved 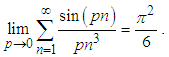 Similarly, when
Similarly, when 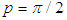 then Eq.(34) reduces to Eq.(27).
then Eq.(34) reduces to Eq.(27).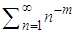 for any even number m,
for any even number m, 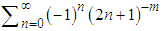 for any odd number m,
for any odd number m, 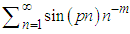 for any odd number m,
for any odd number m, 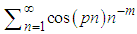 for any even number mand others.Thus, this paper illustrates the strength of the Sampling Theorem to derive the summation of infinite series.
for any even number mand others.Thus, this paper illustrates the strength of the Sampling Theorem to derive the summation of infinite series. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
 (confined by the vertical dotted lines)
(confined by the vertical dotted lines)