-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2018; 8(1): 20-26
doi:10.5923/j.ajsp.20180801.03

A Fast Fractional-Pixel Search Algorithm Based on Linear-Prediction Motion Estimation
Lung-Jen Wang, Wen-Ming Tai
Dept. of Computer Science and Information Engineering, National Pingtung University, Taiwan, R.O.C.
Correspondence to: Lung-Jen Wang, Dept. of Computer Science and Information Engineering, National Pingtung University, Taiwan, R.O.C..
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The fractional-pixel motion estimation is used accurately for motion vector prediction in the H.264/AVC video coding. Based on the linear prediction and a small diamond search algorithm, a fast fractional-pixel search algorithm is proposed in this paper. The proposed method substantially solves the complexity of the calculation of the fractional-pixel motion estimation needed in the H.264/AVC video coding if the image resolution is increased. Finally, experimental results show that the proposed algorithm is superior in performance and reduces around 60% computations for the fractional-pixel calculations.
Keywords: Fractional-pixel, Motion estimation, Linear prediction, H.264/AVC
Cite this paper: Lung-Jen Wang, Wen-Ming Tai, A Fast Fractional-Pixel Search Algorithm Based on Linear-Prediction Motion Estimation, American Journal of Signal Processing, Vol. 8 No. 1, 2018, pp. 20-26. doi: 10.5923/j.ajsp.20180801.03.
Article Outline
1. Introduction
- The H.264/AVC algorithm is one of the international standard of video coding technique [1, 2]. To improve the accuracy of motion estimation in the H.264/AVC video coding, a fractional-pixel motion estimation algorithm is almost mandatory [3, 4]. In addition, it is used the interpolation process to estimate the fractional pixel (1/2-pel and 1/4-pel) positions between the existing positions for the motion vector prediction in the reference image which is magnified in image resolution. In the typical hierarchical fractional-pixel search (HFPS) algorithm [2] shown in Fig.1, at least 8 positions are required for the 1/2-pel, and 16 positions are required for the 1/4-pel, respectively. The disadvantage of the 1/2-pel and 1/4-pel fractional pixel search algorithm is that the computations required are becoming very large. Furthermore, if the image resolution is increased, there are needed for additional motion estimation computations that involve considerably more fractional pixels.
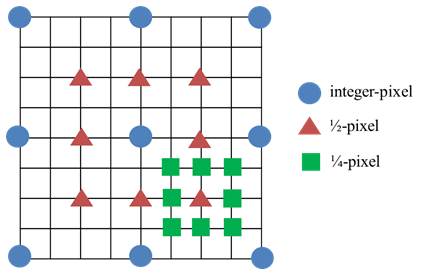 | Figure 1. The hierarchical fractional-pixel search (HFPS) algorithm |
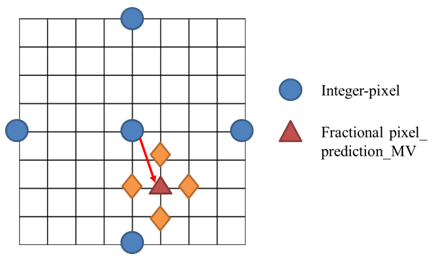 | Figure 2. The small diamond search algorithm |
2. Fractional-Pixel Motion Estimation
- The fractional-pixel motion estimation of the H.264/AVC video coding can be used to improve the inter-frame prediction for video quality [8]. It requires very large computations, such as fractional-pixel (1/2-pel and 1/4-pel) search algorithm and interpolation process. Furthermore, the displacement vector with fractional-pixel resolution can be applied for the motion vector prediction in the H.264/AVC algorithm [10]. To estimate the fractional-pixel displacement, a two-step interpolation process is used as shown in Fig. 3. In the H.264/AVC algorithm, the Wiener filter with six coefficients: [1, -5, 20, 20, -5, 1]/32 is used to interpolate the 1/2-pel positions in first step and an image IW is generated after the first interpolation step. In addition, the bilinear interpolation filter is used to interpolate the 1/4-pel positions and an image IB is generated after the second interpolation step. Fig. 4 shows the interpolation relationship between the integer-pel positions (black), the 1/2-pel positions (gray) and the 1/4-pel positions (white) [5].
 | Figure 3. Two-step interpolation process used in H.264/AVC |
 | Figure 4. Example of interpolation relationship for filter size 6×6 |
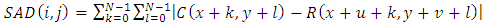 | (1) |
|
3. The Proposed LFFS Algorithm
3.1. Linear Prediction
- In this paper, a linear prediction based the fractional -pixel motion estimation and the center-biased fractional-pixel search (CBFPS) [3] is developed, first estimates horizontal components and next vertical components for the fractional-pixel motion vector and its sum of absolute difference error surface. Figs. 5 and 6 show the linear prediction of fractional-pixel error surface in the horizontal and vertical directions, respectively. In Fig. 5 for the x-axis (horizontal direction), let
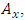
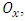 and
and 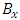 be integer-pixel points, and
be integer-pixel points, and 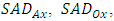 and
and 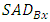 are their corresponding SADs.
are their corresponding SADs. 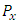 is selected point between
is selected point between 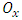 and
and 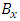 points such that the slopes of two lines
points such that the slopes of two lines 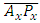 and
and 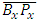 are equal as follows.
are equal as follows.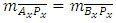 | (2) |
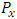 in a predicted minimum point and
in a predicted minimum point and 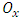 in a fractional-pixel point, and
in a fractional-pixel point, and 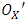 be a point in
be a point in 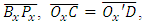
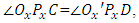 and
and 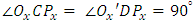 . The distance s can be obtained by
. The distance s can be obtained by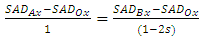 | (3) |
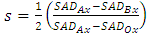 | (4) |
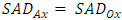 , let
, let 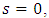 i.e., the integer-pixel motion vector is selected as the final motion vector. Similarly, let t be selected distance between a predicted minimum point and a fractional-pixel point in the y-axis (vertical direction) for the fractional-pixel motion vector. As shown in Fig. 6, the distance t can be given by
i.e., the integer-pixel motion vector is selected as the final motion vector. Similarly, let t be selected distance between a predicted minimum point and a fractional-pixel point in the y-axis (vertical direction) for the fractional-pixel motion vector. As shown in Fig. 6, the distance t can be given by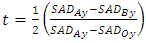 | (5) |
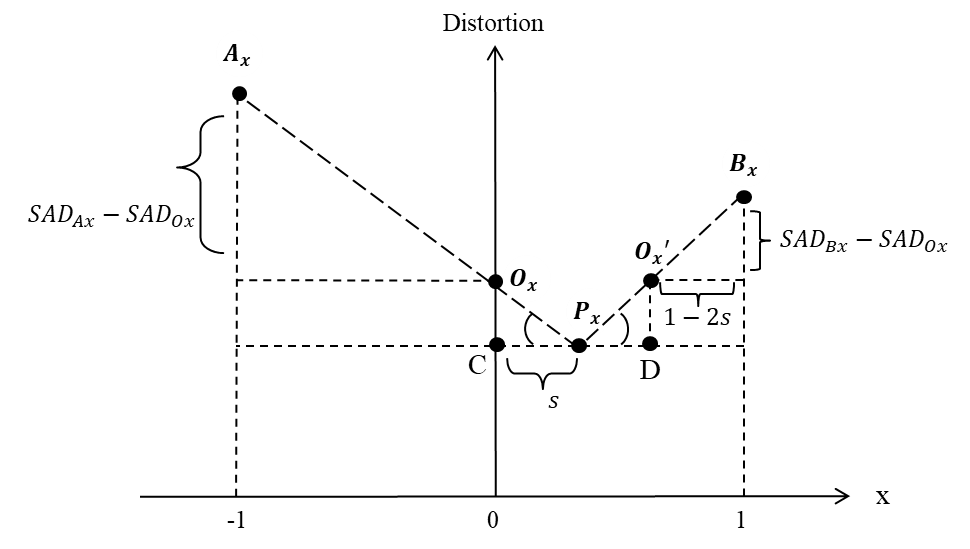 | Figure 5. A linear prediction fractional-pixel error surface in x-axis |
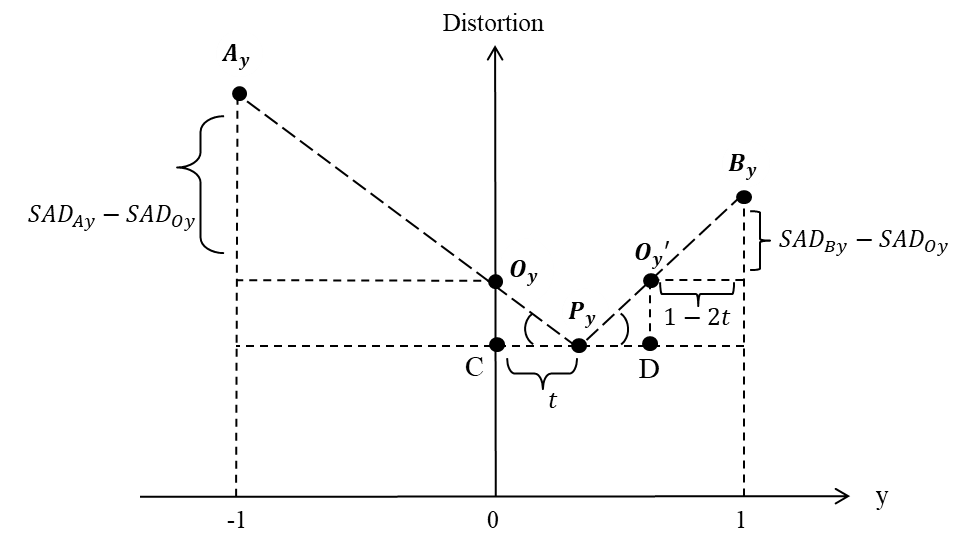 | Figure 6. A linear prediction fractional-pixel error surface in y-axis |
3.2. LFFS with a Small Diamond Search
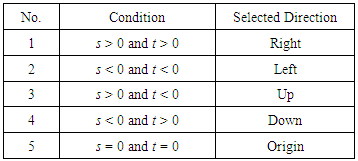
- In this paper, the LFFS algorithm combines (4) and (5) as the fractional-pixel search direction as follows.
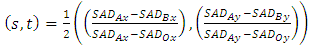 | (6) |
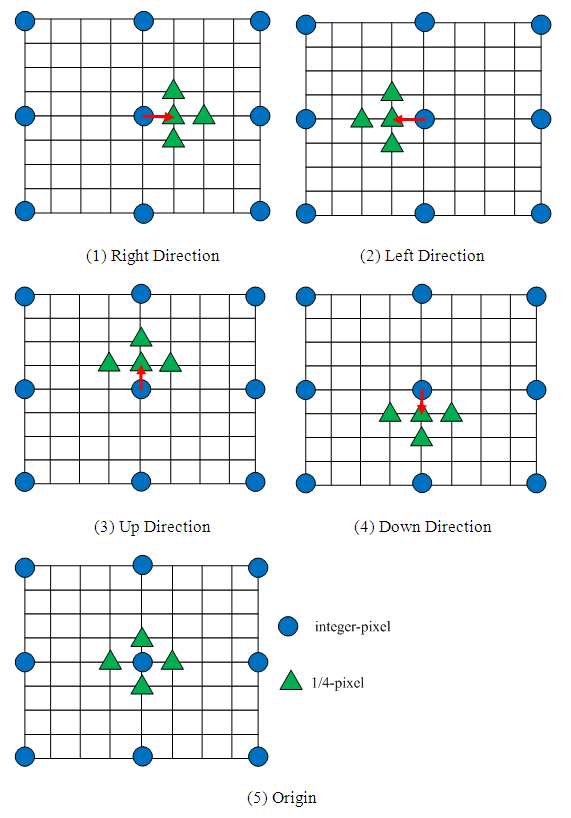 | Figure 7. Directional selections based small diamond search |
|
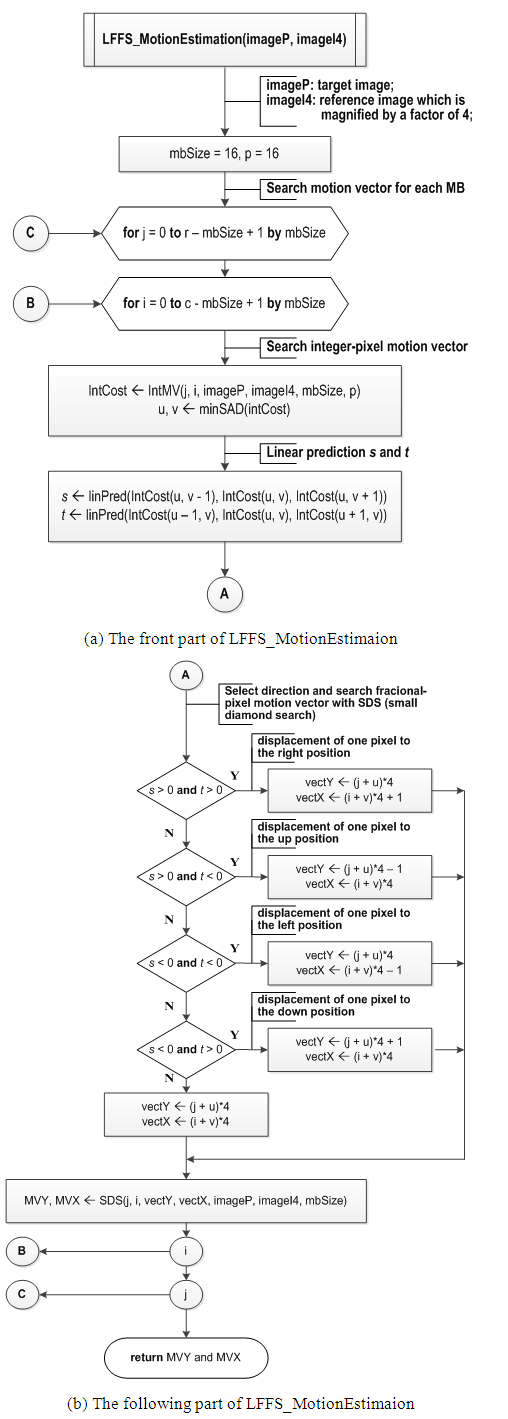 | Figure 8. The flow chart of the proposed LFFS algorithm |
4. Experimental Results
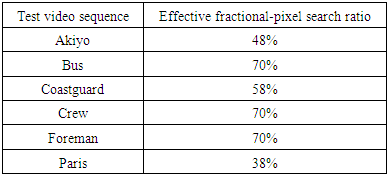
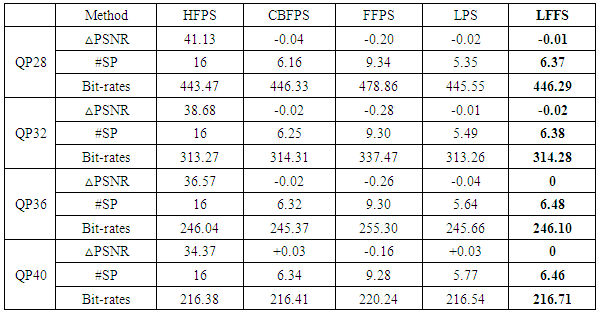
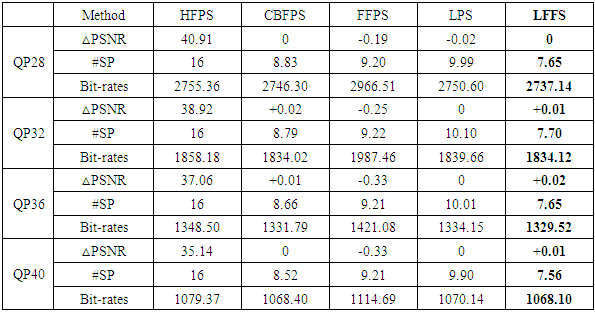
- In this paper, the proposed LFFS method is compared with the Hierarchical Fractional Pixel Search (HFPS) [2], the Center Biased Fractional Pixel Search (CBFPS) [3], the Fast Fractional Pixel Search (FFPS) [6], and the Linear Prediction Search (LPS) [7]. Performance comparisons are carried out on some standard CIF (Akiyo, Bus, Coastguard, Crew, Foreman, Paris) and 4CIF (City, Harbour, Ice, Soccer) video sequences shown in Figs. 9 and 10, and based on the H.264/AVC JM 18.0 [11].
 | Figure 9. Some standard video test sequences (CIF) |
 | Figure 10. Some standard video test sequences (4CIF) |
|
|
5. Conclusions
- In the H.264/AVC standard, the typical HFPS algorithm is used to improve the fractional-pixel motion estimation. This HFPS method requires at least 8 positions for the 1/2-pel, and 16 positions for the 1/4-pel, respectively, in the fractional-pixel motion estimation. However, if the image resolution is increased, the computations required for the fractional-pixel motion estimation are mandatory increased. In order to reduce the additional calculations of the fractional-pixel motion estimation needed in the H.264/AVC algorithm, the linear-prediction fast fractional-pixel search algorithm, called LFFS method, is developed in this paper. In this method, both linear prediction and small diamond search are proposed. Furthermore, the proposed LFFS method substantially reduces 60% and 52% computations for the fractional-pixel motion estimation in CIF and 4CIF video sequences, respectively, and still achieves a better quality of reconstructed image. That is, the proposed method for the fractional-pixel motion estimation in the H.264/AVC standard is that it substantially reduces the computation complexity and also increases the precision of motion vector prediction.
ACKNOWLEDGEMENTS
- This work was supported by the Ministry of Science and Technology, R.O.C., under Grant MOST 104-2221-E-153-010, 106-2622-E-153-001-CC2 and 106-2221-E-153-006.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML