1. Introduction

One of the primary objectives of numerical analysis is to decide which algorithms can be implemented to solve mathematical problems on computer [1]. These algorithms accurately approximate the solution of problems which the latter can't be solved exactly and after that a typical techniques for estimating error bounds for the approximation process can be handled [2]. Many researches focused their attention toward using such methods to solve their problems. C. Thinzar and N. Aye made use of the digital image correlation that is based on the sub-pixel accuracy with the aid of Newton Raphson method to detect storm direction for managing and to prevent the possible land's attacked region [3]. D. Biolè, etc. used Secant method in addition to other techniques to measure apparent contact angles of non-axisymmetric drops [4]. Md. G. Moazzam, etc. used a robust method for solving transcendental equations. The presented method by them gave better results rather than the well-known False Position method and the Bisection method for solving such equations [5]. W. Chu, etc. demonstrated a new registration algorithm based on Newton Raphson iteration process to align images with rigid body transformation [6]. So, an attempt to detect error propagation which can be occurred by applying such numerical methods to digital image had been utilized here. These methods are:

1.1. Bisection Method

It is one of the most basic problems of numerical approximation. It is also known as the root-finding problem or Binary-search method. It is a process of dividing a set continually in half to search for the solution to a certain problem [2]. It states that if f(x) is a continuous function defined on the interval a<x<b, with f(a) and f(b) of opposite sign, then there is at least one root in the interval between a and b [5]. By setting a₁=a and b₁=b and take the midpoint of [a,b] such that [7, 8]

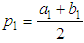(1)

So the next steps must be taken in the considerations:

• If f(p₁)=0; a root was found at p₁.

• If f(a₁).f(b₁)<0, then there is a root between a₁ and p₁.

• If f(a₁).f(b₁)>0, then there is a root between p₁ and b₁. And so on.

1.2. Newton Raphson Method

It is one of the well-known numerical approaches for solving a root-finding problem [2]. This technique supposes that p_o be an approximation to the root (i.e. iteration guess) and belongs to the interval [a,b] in such that f '(p_o)≠0 and |p-p_o| is so small and hence [7, 9]

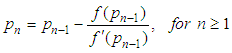(2)

1.3. Secant Method

This method uses a secant line joining two points that cut curve's function and can be presented in the following expression [2, 8]:

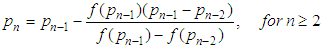(3)

1.4. False Position Method

In this technique, one uses results that are known to be false to converge to the true root. This method chooses an initial approximations p_o and p₁ such that f(p_o).f(p₁)<0. The new approximation value will be then obtained in the way as described in the secant method mentioned above. After that and in order to decide which secant line to be used, the product of f(p₂) and f(p₁) should be taken and one of the following considerations shall be verified [7]:

• Choose p₃ as a line joining (p₁,f(p₁)) and (p₂,f(p₂)) if f(p₁).f(p₂)<0.

• Choose p₃ as a line joining (p_o,f(p_o)) and (p₂,f(p₂)) if f(p₁).f(p₂)>0.

In order to estimate the approximation errors, two methods had been used here; these are the absolute and relative errors as shown in the following expressions [2]:

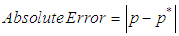(4)

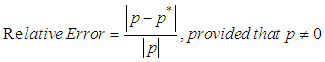(5)

Where p* is an approximation value for p.

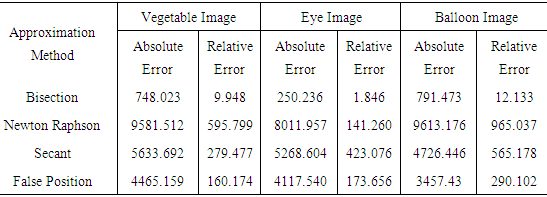
2. Result and Discussion

For simplicity, an assumption had been made here that the root in the interval (i.e. image's data) is unique and the stopping criteria shall be as follows:

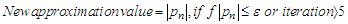(6)

where ε is the tolerance. Figure (1) shows the used images with their fitting histograms' curves. The fitting process had been executed by using Table Curve 2D V 5.01 program.

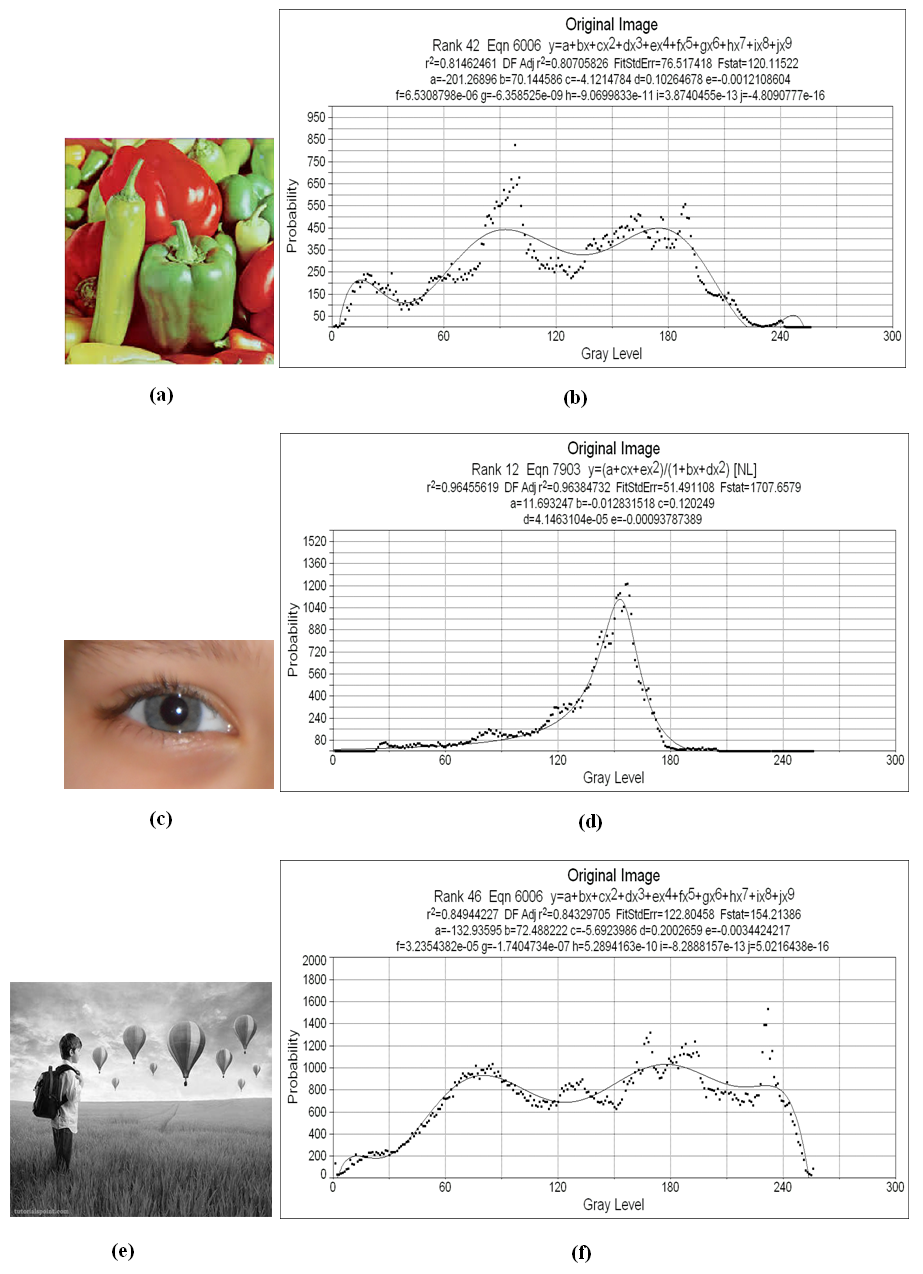Figure 1. (a) Vegetable image, (b) fitting histogram for (a), (c) Eye Image, (d) fitting histogram for (c), (e) Balloon image, (f) fitting histogram for (e)

In general and as a result of application, numerical approximation methods distorted the images in alternatives ratios depending on image's histogram. An image with sharp chromatic gradient is better than other used images which have a wide range of color gradients, this can be seen through noticing Figs. (2-4). In addition to that, one can noticed that there is no clear sequence for algorithms' effects upon single image. In most cases, one can find that the best numerical methods' performance is the Bisection method with lowest errors presented in Table (1).

Table 1. Approximation Errors for all used images

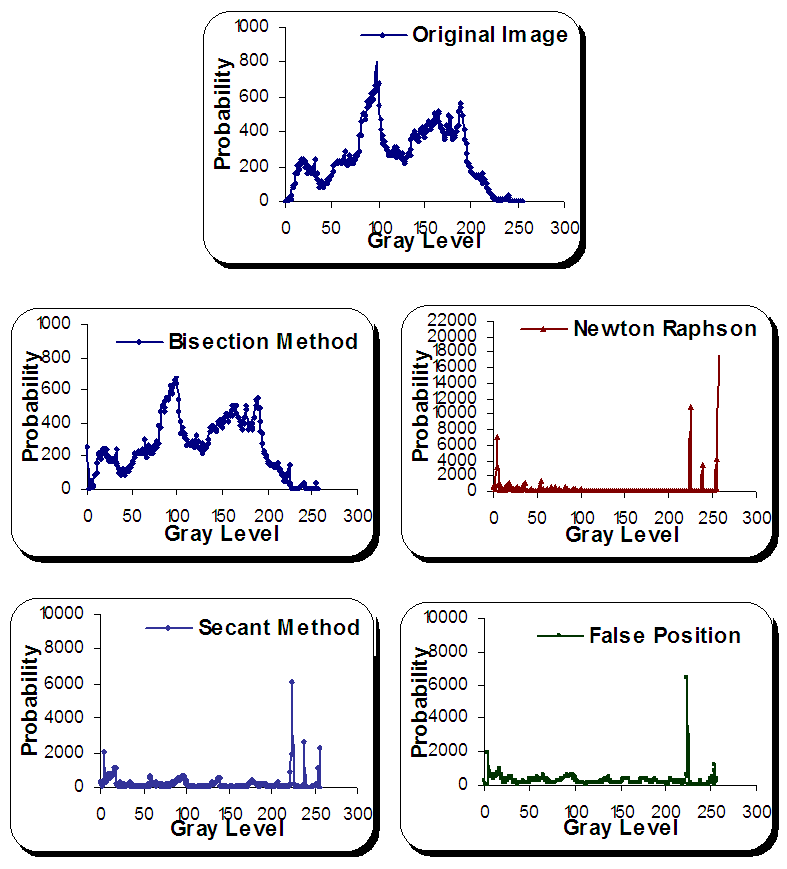Figure 2. Histograms for vegetable image before and after numerical methods' applications

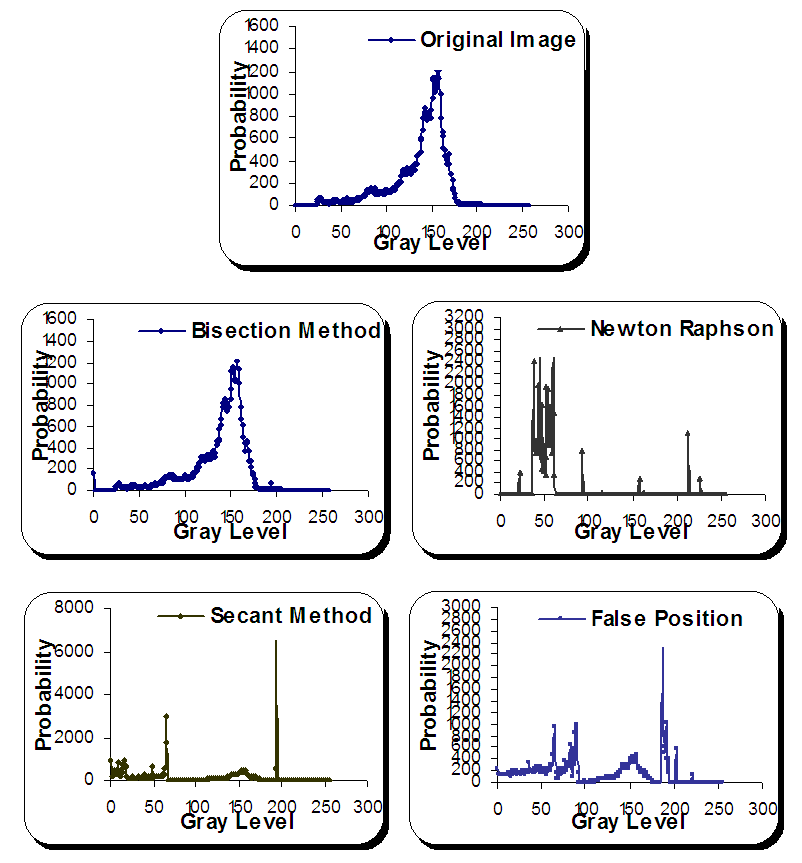Figure 3. Histograms for eye image before and after numerical methods' applications

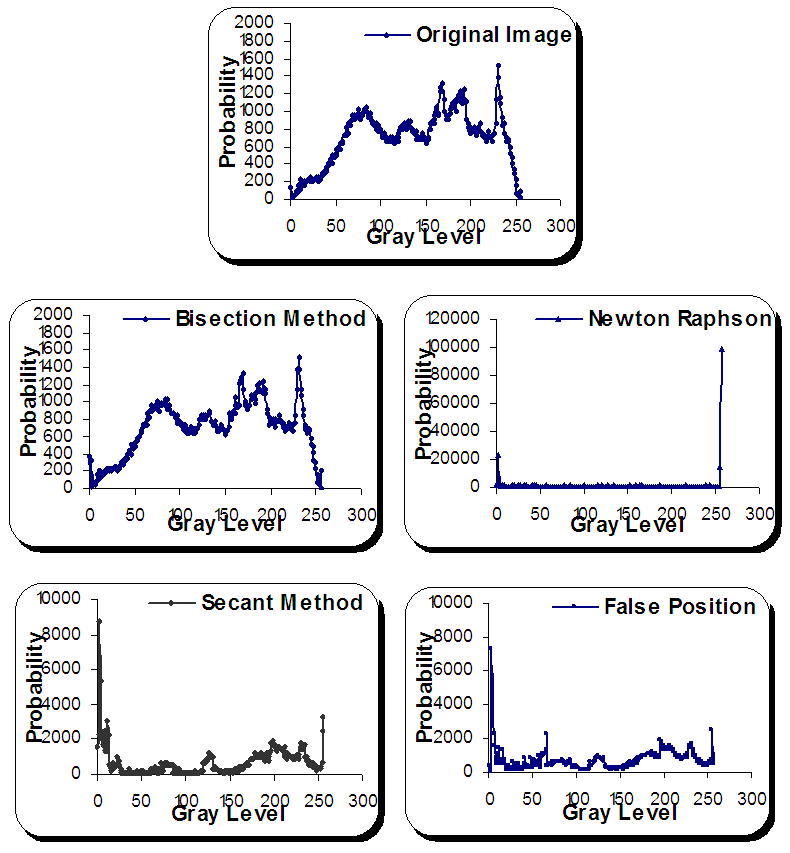Figure 4. Histograms for balloon image before and after numerical methods' applications

A distorted case occurred in eye image in the application of the Newton Raphson method with a shift toward lower values of the image's gray level while it isn't the case for other used images; the distortion case resulted near the ends of images' gray levels for all used algorithms in general, this can be recognized through noticing approximation errors explained in the above table. Image's histogram restricts the sequence of algorithms in their applications; the symmetric behavior for both Secant and False Position methods resulted in the case of vegetable and balloon images in contraction to that occurred to the case in eye image which the latter witnessed a strong distortion state in the case of Secant method technique.

3. Conclusions

By assumption that the root is exist in image's gray level interval, an attempt to explorer the application of some numerical algorithms is tested here by using some numerical analysis algorithms. As a consequence result, one can noticed that the used numerical algorithms distorted the image after all with different distortion ratios depend upon image's histogram. In addition to that, the sequence for techniques' effects is not clear upon such used images but in general one can be concluded that the Bisection method can be recognized as the best one with least absolute and relative errors.