| [1] | L. Quan, L. Pei-Yue, Z. Ming-chao, S. Yong-xin, Y. Huai-jiang, “A novel image encryption algorithm based on chaos maps with Markov properties,” Communications in Nonlinear Science and Numerical Simulation, vol. 20, pp. 506-515, 2015. |
| [2] | J.-X. Chen, Z.-L. Zhu, C. Fu, H. Yu, L.-B. Zhang, “A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism,” Communications in Nonlinear Science Numerical Simulation, vol. 20, pp. 846-860, 2015. |
| [3] | H. Zhu, C. Zhao, X. Zhang, “A novel image encryption-compression scheme using hyper-chaos and Chinese remainder theorem,” Signal Process: Image Communication, vol. 28, pp. 670-680, 2013. |
| [4] | Y. Wang, K.-W. Wong, X. Liao, G. Chen, “A new chaos-based fast image encryption algorithm,” Applied Soft Computing, vol. 11, pp. 514-522, 2011. |
| [5] | H. Zhu, C. Zhao, X. Zhang, L. Yang, “An image encryption scheme using generalized Arnold map and affine cipher,” Optik, vol. 125, pp. 6672-6677, 2014. |
| [6] | L. Y. Zhang, C. Li, K.-W. Wong, S. Shu, G. Chen “Cryptanalyzing a chaos-based image encryption algorithm using alternate structure,” Journal of Systems and Software, vol. 85, pp. 2077-2085, 2012. |
| [7] | S. Som, S. Sen, “A Non-adaptive partial encryption of grayscale images based on chaos,” Procedia Technology, vol. 10, pp. 663-671, 2013. |
| [8] | M. Türk, H. Oğraş, “Recognition of multi-scroll chaotic attractors using wavelet-based neural network and performance comparison of wavelet families,” Expert Systems with Applications, vol. 37, pp. 8667-8672, 2010. |
| [9] | J.-H. Lee, H.-G. Ryu, “High security wireless CDSK-based chaos communication with new chaos map,” Military communications conference IEEE, MILCOM, pp. 786-790, 2013. |
| [10] | S.-W. Yoon, J.-H. Lee, H.-G. Ryu, “Chaos communication system using MIMO technique,” Advanced communication technology conference ICACT, pp. 579-583, 2014. |
| [11] | N. Jiang, et al. “Chaos synchronization and communication in multiple time-delayed coupling semiconductor lasers driven by a third laser,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 17, pp. 1220-1227, 2011. |
| [12] | Z. Kang, J. Sun, L. Ma, Y. Qi, S. Jian, “Multimode synchronization of chaotic semiconductor ring laser and its potential in chaos communication,” IEEE Journal of Quantum Electronics, vol. 50, pp. 148-157, 2014. |
| [13] | J. Yang, Y. Chen, F. Zhu, “Associated observer-based synchronization for uncertain chaotic systems subject to channel noise and chaos-based secure communication,” Neurocomputing, vol. 167, pp. 587-595, 2015. |
| [14] | M. Eisencraft, et al. “Chaos-based communication systems in non-ideal channels,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, pp. 4707-4718, 2012. |
| [15] | G. A. Abib, M. Eisencraft, “On the performance of a digital chaos-based communication system in noisy channels,” Modelling, identification and control of nonlinear systems conference MICNON, vol. 48, no. 11, pp. 976-981, 2015. |
| [16] | G. Kaddoum, M. Coulon, D. Roviras, P. Charge, “Theoretical performance for asynchronous multi-user chaos-based communication systems on fading channels,” Signal Processing, vol. 90, pp. 2923-2933, 2010. |
| [17] | J. Hu, J. Ma, J. Lin, “Chaos synchronization and communication of mutual coupling lasers ring based on incoherent injection,” Optik, vol. 121, pp. 2227-2229, 2010. |
| [18] | J. Yang, F. Zhu, “Synchronization for chaotic systems and chaos-based secure communications via both reduced-order and step-by-step sliding mode observers,” Communications in Nonlinear Science and Numerical Simulation, vol. 18, pp. 926-937, 2013. |
| [19] | X.-L. An, et al. “Design of a new multistage chaos synchronized system for secure communications and study on noise perturbation,” Mathematical and Computer Modelling, vol. 54, pp. 7-18, 2011. |
| [20] | A. A. Zaher, A. Abu-Rezq, “On the design of chaos-based secure communication systems,” Communications in Nonlinear Science and Numerical Simulation, vol. 16, pp. 3721-3737, 2011. |
| [21] | M. Türk, H. Oğraş, “Classification of chaos-based digital modulation techniques using wavelet neural networks and performance comparison of wavelet families,” Expert Systems with Applications, vol. 38, pp. 2557-2565, 2011. |
| [22] | Z.-L. Zhu, W. Zhang, K.-W. Wong, H. Yu, “A chaos-based symmetric image encryption scheme using a bit-level permutation,” Information Sciences, vol. 181, pp. 1171-1186, 2011. |
| [23] | V. Patidar, N. K. Pareek, G. Purohit, K. K. Sud, “A robust and secure chaotic standard map based pseudorandom permutation-substitution scheme for image encryption,” Optics Communications, vol. 284, pp. 4331-4339, 2011. |
| [24] | M. A. Murillo-Escobar, C. Cruz-Hernandez, F. Abundiz-Perez, R. M. Lopez-Gutierez, O. R. Acosta Del Campo, “A RGB image encryption algorithm based on total plain image characteristics and chaos,” Signal Processing, vol. 109, pp. 119-131, 2015. |
| [25] | R. Ye, “A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism,” Optics Communications, vol. 284, pp. 5290-5298, 2011. |
| [26] | R. Ye, W. Guo, “An image encryption scheme based on chaotic systems with changeable parameters,” I. J. Computer network and Information Security, vol. 4, pp. 37-45, 2014. |
| [27] | A. N. K Telem, C. M. Segning, G. Kenne, H. B. Fotsin, “A simple and robust gray image encryption scheme using chaotic Logistic map and artificial neural network,” Advanced in Multimedia, vol. 2014, 13 pages, 2014. |
| [28] | W. Yibei, L. Man, X. Yanting, C. Hougui, “Research on chaos phenomena in power system,” Power Engineering and Automation Conference, vol. 2, pp. 453-456, 2011. |
| [29] | I. M. Ginarsa, A. Soeprijanto, M. H. Purnomo, “Controlling chaos and voltage collapse using an ANFIS-based composite controller-static var compensator in power systems,” International Journal of Electrical Power & Energy Systems, vol. 46, pp. 79-88, 2013. |
| [30] | H.-T. Yau, M.-H. Wang, T.-Y. Wang, G. Chen, “Signal clustering of power disturbance by using chaos synchronization,” International Journal of Electrical Power & Energy Systems, vol. 64, pp. 112-120, 2015. |
| [31] | M. Ghasemi, S. Ghavidel, J. Aghaei, M. Gitizadeh, H. Falah,, “Application of chaos-based chaotic invasive weed optimization techniques for environmental OPF problems in the power systems,” Chaos, Solitons & Fractals, vol. 69, pp. 271-284, 2014. |
| [32] | Q. Chen, X. Ren, J. Na, “Robust finite-time chaos synchronization of uncertain permanent magnet synchronous motors,” ISA Transactions, vol. 58, pp. 262-269, 2015. |
| [33] | X. Zhou, J. Li, Y. Ma, “Chaos phenomena in DC-DC converter and chaos control,” Procedia Engineering, vol. 29, pp. 470-473, 2012. |
| [34] | E. Avaroğlu, İ. Koyuncu, A. B. Özer, M. Türk, “Hybrid pseudo-random generator for cryptographic systems,” Nonlinear Dynamics, vol. 82, pp. 239-248, 2015. |
| [35] | J. W. Yoon, H. Kim, “An image encryption scheme with a pseudorandom permutation based on chaotic maps,” Communications in Nonlinear Science and Numerical Simulation, vol. 15, pp. 3998-4006, 2010. |
| [36] | E. Avaroğlu, T. Tuncer, A. B. Özer, B. Ergen, M. Türk, “A novel chaos-based post-processing for TRNG,” Nonlinear Dynamics, vol. 81, pp. 189-199, 2015. |
| [37] | F. Elgendy, et al. “Chaos-based model for encryption and decryption of digital images,” Multimedia Tools and Applications, vol. 75, pp. 11529-11553, 2016. |
| [38] | B. Norouzi, S. Mirzakuchaki, S. M. Seyedzadeh, M. R. Mosavi, “A simple, sensitive and secure image encryption algorithm based on hyper-chaotic system with only one round diffusion process,” Multimedia Tools and Applications, vol. 71, pp. 1469-1497, 2014. |
| [39] | Y. Zhang, D. Xiao, W. Wen, M. Li, “Breaking an image encryption algorithm based on hyper-chaotic system with only one round diffusion process,” Nonlinear Dynamics, vol. 76, pp. 1645-1650, 2014. |
| [40] | C. Fu, S. Hou, W. Zhou, W.-Q. Liu, D.-L. Wang, “A Chaos-based image encryption scheme with a plaintext related diffusion,” International Conference on Information, Communications and Signal Processing, pp. 1-5, 2013. |
| [41] | H. Xue, S. Wang, X. Meng, “Study on one modified chaotic system based on Logistic map,” Research Journal of Applied Sciences, Engineering and Technology, vol. 5, pp. 898-904, 2013. |
| [42] | A. Pande, J. Zambreno, “A chaotic encryption scheme for real-time embedded systems: design and implementation,” Telecommunication systems, vol. 52, pp. 551-561, 2013. |
| [43] | J. Ahmad, S. O. Hwang, “A secure image encryption scheme based on chaotic maps and affine transformation,” Multimedia Tools and Applications, vol. 75, pp. 13951-13976, 2016. |
| [44] | H. M. Hathal, R. A. Abdulhussein, S. K. Ibrahim, “Lyapunov exponent testing for AWGN Generator system,” Communications and Network, vol. 6, pp. 201-208, 2014. |
| [45] | K. Marton, A. Sucıu, C. Sacarea, O. Cret, “Generation and testing of random numbers for cryptographic applications,” Proceedings of the Romanian Academy, vol. 13, pp. 368-377, 2012. |
| [46] | A. Rukhin, et al. “A statistical test suite for random and pseudorandom number generators for cryptographic applications,” NIST Special Publication 800-22 rev1, 2010. |
| [47] | H. Liu, A. Kadir, Y. Niu, “Chaos-based color image block encryption scheme using S-box,” International Journal of Electronics and Communications, vol. 68, pp. 676-686, 2014. |
| [48] | X.-J. Tong, M. Zhang, Z. Wang, J. Ma, “A joint color image encryption and compression scheme based on hyper-chaotic system,” Nonlinear Dynamics, vol. 84, pp. 2333-2356, 2016. |


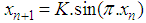
 and
and 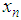 is in (0,1). For instance, if
is in (0,1). For instance, if 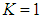 , then the map is in chaos state, which means that output sequence
, then the map is in chaos state, which means that output sequence 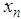 is aperiodic, non-convergent and very sensitive to initial value
is aperiodic, non-convergent and very sensitive to initial value 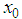 . However, some isolated values such as
. However, some isolated values such as 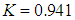 appear to show non-chaotic behavior and generates periodic sequences at output which are not random and unsuitable for encryption. In cryptographic manner, if the control parameter is used as a key, then this situation will reduce the key space size. Consequently, a new one-dimensional chaotic map should be designed and its all parameters make the system truly chaotic and provide larger key space.
appear to show non-chaotic behavior and generates periodic sequences at output which are not random and unsuitable for encryption. In cryptographic manner, if the control parameter is used as a key, then this situation will reduce the key space size. Consequently, a new one-dimensional chaotic map should be designed and its all parameters make the system truly chaotic and provide larger key space.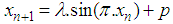
 values are restricted to the interval of [
values are restricted to the interval of [ ] with
] with 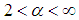 . In Eq. (2), the maximum point occurs at
. In Eq. (2), the maximum point occurs at 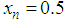 and its value is
and its value is 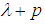 , while the minimum occurs at
, while the minimum occurs at  and its value is
and its value is 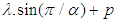 . Thus,
. Thus,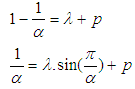
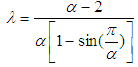 and
and 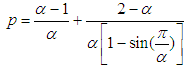 . Substituting these values to the (2), we obtain the following final equation.
. Substituting these values to the (2), we obtain the following final equation.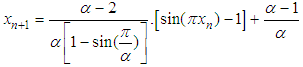
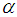 determines the interval in which range
determines the interval in which range 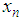 distributes.
distributes. 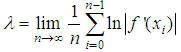
 can be used to generate different outputs which improves the key space of the cryptosystem.
can be used to generate different outputs which improves the key space of the cryptosystem. 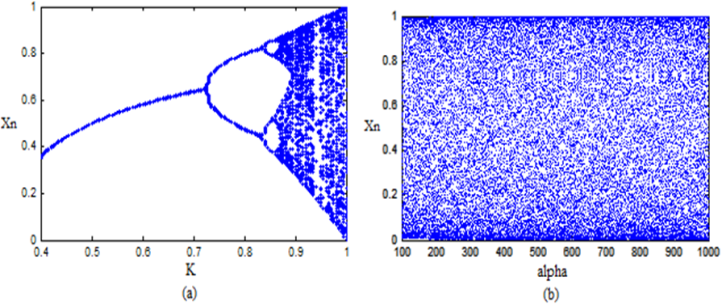
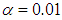 ), then the statistical test is passed successfully and the generator is considered as random with 99% confidence. NIST uses bit streams for analysis. In order to get sequential bit streams, the following transformation is applied to the output of the ISM.
), then the statistical test is passed successfully and the generator is considered as random with 99% confidence. NIST uses bit streams for analysis. In order to get sequential bit streams, the following transformation is applied to the output of the ISM.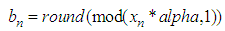
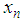 value to (0,1). Using Eq. (6), a bit value ‘1’ or ‘0’ is generated for each
value to (0,1). Using Eq. (6), a bit value ‘1’ or ‘0’ is generated for each 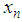 . For instance, the system parameters of
. For instance, the system parameters of 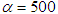 and
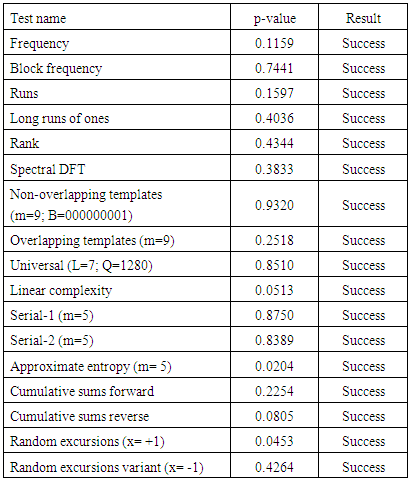
and 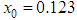 are chosen to generate 1,000,000 bits to carry on NIST. The results are given in Table 1.
are chosen to generate 1,000,000 bits to carry on NIST. The results are given in Table 1. 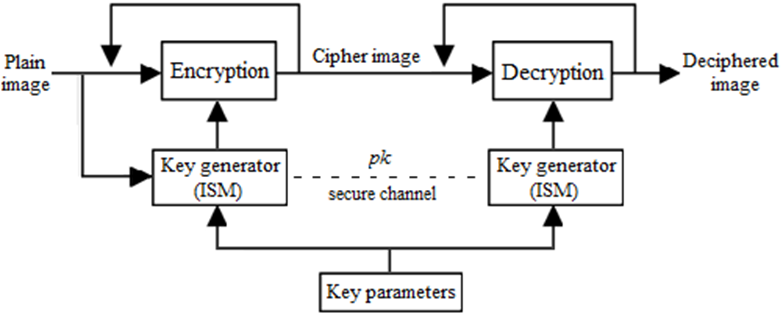
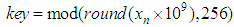
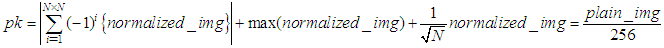
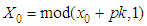
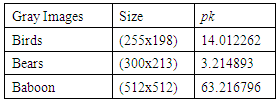
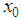 is the first initial secret key which will be modified by pk.If only one pixel is changed by a bit value in the plain image, then it will be a slight change in pk which supplies a small change in the initial condition of the ISM and results totally different keys for encryption. For example, when the value of one pixel in the birds image,
is the first initial secret key which will be modified by pk.If only one pixel is changed by a bit value in the plain image, then it will be a slight change in pk which supplies a small change in the initial condition of the ISM and results totally different keys for encryption. For example, when the value of one pixel in the birds image, 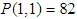 is changed to
is changed to 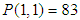 (one bit different), with the same key parameters of
(one bit different), with the same key parameters of  and
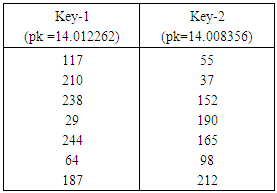
and 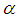 , then the some part of the obtained encryption keys are listed in Table 3.
, then the some part of the obtained encryption keys are listed in Table 3. 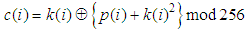
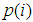 ,
,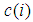 and
and 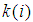 represent current plain pixel, output cipher pixel and secret key, respectively. Modular operation is used to limit the cipher data to the range of [0, 255]. Such a diffusion function is very efficient because simple modular arithmetic and logical operations can be performed in high speed. To increase the security of the cryptosystem, encryption process is iterated several times with different keys. The proposed scheme has a symmetric algorithm which means that identical key is used for decryption. The decryption algorithm is the reverse encryption and defined by the following equation.
represent current plain pixel, output cipher pixel and secret key, respectively. Modular operation is used to limit the cipher data to the range of [0, 255]. Such a diffusion function is very efficient because simple modular arithmetic and logical operations can be performed in high speed. To increase the security of the cryptosystem, encryption process is iterated several times with different keys. The proposed scheme has a symmetric algorithm which means that identical key is used for decryption. The decryption algorithm is the reverse encryption and defined by the following equation.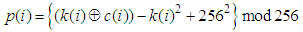
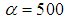 ,
, and
and  . The result is shown in Fig. 4.
. The result is shown in Fig. 4.
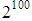 [5] to make brute-force attack infeasible. In our encryption scheme, key parameters are:
[5] to make brute-force attack infeasible. In our encryption scheme, key parameters are: 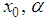 and
and 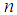 . According to the IEEE floating-point standard [2], the computational precision of the 64-bit double precision number is about
. According to the IEEE floating-point standard [2], the computational precision of the 64-bit double precision number is about 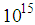 . In our cryptosystem,
. In our cryptosystem, 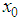 and
and 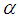 keys are floating point and
keys are floating point and 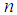 is 8-bit key. Hence, the total number of possible secret key is approximately,
is 8-bit key. Hence, the total number of possible secret key is approximately, 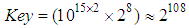
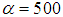 ,
,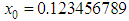 and
and 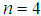 . Then a slight change is applied to the one of the parameters with others remain same, then repeats the encryption. Key-2 is
. Then a slight change is applied to the one of the parameters with others remain same, then repeats the encryption. Key-2 is 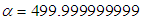 ,
,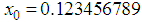 ,
,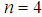 ; Key-3 is
; Key-3 is 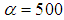 ,
,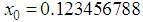 ,
,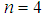 and Key-4 is
and Key-4 is 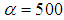 ,
,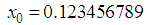 ,
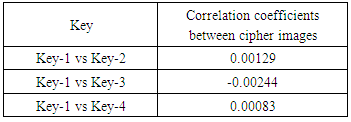
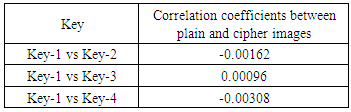
,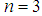 . Then we have computed correlation coefficients for the ciphered images and the results have been given in Table 4.
. Then we have computed correlation coefficients for the ciphered images and the results have been given in Table 4.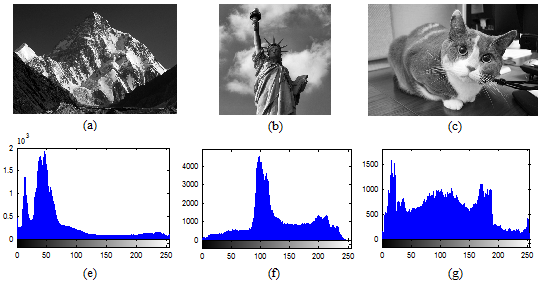
 799) (b) liberty statue (512
799) (b) liberty statue (512  512) (c) cat (505
512) (c) cat (505  330)
330)
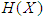 represents the entropy of an information source
represents the entropy of an information source 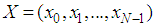 with a length of N, then the entropy will be:
with a length of N, then the entropy will be: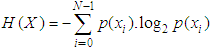
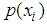 the probability of symbol
the probability of symbol  and the entropy is expressed in bits. If a truly random source emitting
and the entropy is expressed in bits. If a truly random source emitting 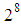 symbols as
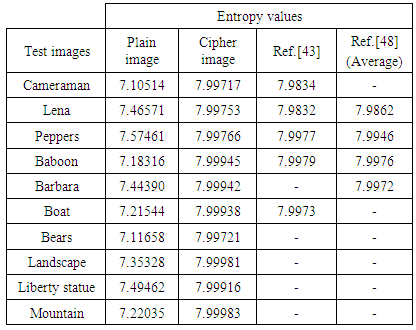
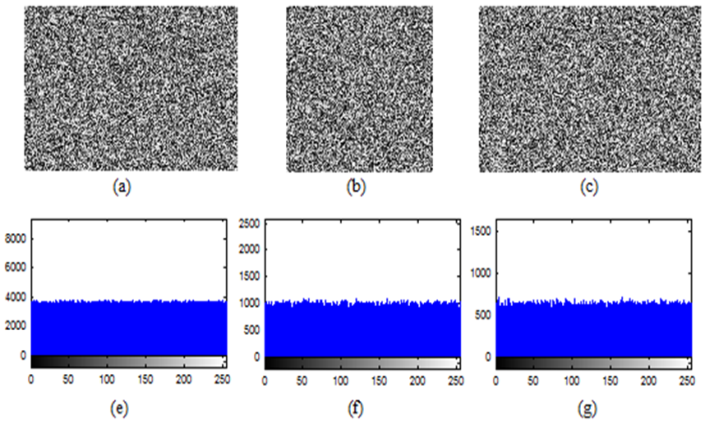
symbols as 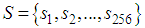 with equal probability, then, the entropy will be calculated to 8. For a practical information source, its entropy value is smaller than the ideal one. Generally, the more uncertain or random source is, the more information entropy it will contain [3]. Maximum entropy is achieved in the case of a uniform probability distribution. Ten gray test images (Cameraman, Lena, Peppers, Baboon, Barbara, Boat, Bears, Landscape, Liberty statue and Mountain) are encrypted using the proposed cryptosystem with Key-1. Table 6 shows the entropy results and comparison with other existing algorithms. Entropy values of the proposed scheme are greater than the values obtained by [43] and [48].
with equal probability, then, the entropy will be calculated to 8. For a practical information source, its entropy value is smaller than the ideal one. Generally, the more uncertain or random source is, the more information entropy it will contain [3]. Maximum entropy is achieved in the case of a uniform probability distribution. Ten gray test images (Cameraman, Lena, Peppers, Baboon, Barbara, Boat, Bears, Landscape, Liberty statue and Mountain) are encrypted using the proposed cryptosystem with Key-1. Table 6 shows the entropy results and comparison with other existing algorithms. Entropy values of the proposed scheme are greater than the values obtained by [43] and [48].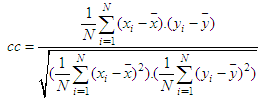
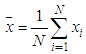 and
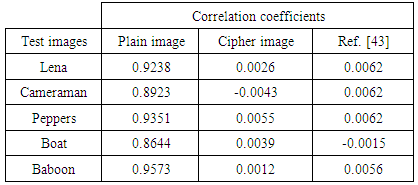
and 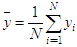 . In (14), N shows the total number of pairs of diagonally adjacent pixels. Five test images are used in the proposed cryptosystem to determine the correlation coefficients of adjacent pixels for diagonally. The result of the correlation coefficients and their corresponding cipher images produced by Key-1 are given in Table 7. From Table 7, compared with the results in [43], our scheme shows superior correlation performance. It is also clear that the proposed scheme significantly reduces the correlation between adjacent pixels of the plain images.
. In (14), N shows the total number of pairs of diagonally adjacent pixels. Five test images are used in the proposed cryptosystem to determine the correlation coefficients of adjacent pixels for diagonally. The result of the correlation coefficients and their corresponding cipher images produced by Key-1 are given in Table 7. From Table 7, compared with the results in [43], our scheme shows superior correlation performance. It is also clear that the proposed scheme significantly reduces the correlation between adjacent pixels of the plain images. 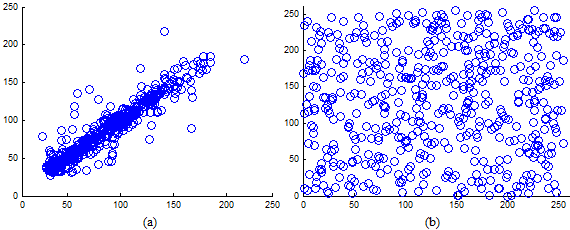
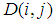 is defined as
is defined as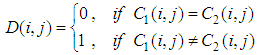
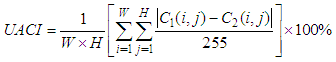
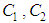 are the two cipher images corresponding to two plain images with only one pixel difference. NPCR measures how many pixels are different between
are the two cipher images corresponding to two plain images with only one pixel difference. NPCR measures how many pixels are different between  and
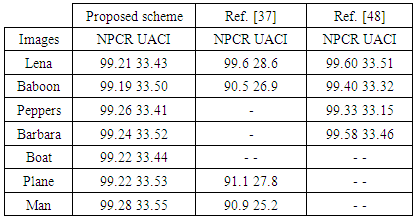
and 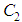 using same encryption key. UACI is used to measure the average intensity of differences between two images. NPCR and UACI values [25] for two random images, which are an expected estimates for an ideal image cryptosystem should be 99.60% and 33.46% respectively. Seven test images are randomly chosen to evaluate the differential attack analysis of the proposed cryptosystem. First, all the test images are encrypted with Key-1, one by one. Then, the pixel value in the middle of the each test image is incremented by one. Afterwards, these images with one pixel difference (just one bit) are encrypted with same Key-1 and results the corresponding cipher test images. For instance, Lena test image
using same encryption key. UACI is used to measure the average intensity of differences between two images. NPCR and UACI values [25] for two random images, which are an expected estimates for an ideal image cryptosystem should be 99.60% and 33.46% respectively. Seven test images are randomly chosen to evaluate the differential attack analysis of the proposed cryptosystem. First, all the test images are encrypted with Key-1, one by one. Then, the pixel value in the middle of the each test image is incremented by one. Afterwards, these images with one pixel difference (just one bit) are encrypted with same Key-1 and results the corresponding cipher test images. For instance, Lena test image  is encrypted to
is encrypted to 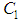 by using Key-1. Then, the value of the pixel in the middle of the Lena image,
by using Key-1. Then, the value of the pixel in the middle of the Lena image, 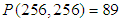 is changed to and the same encryption is performed and results
is changed to and the same encryption is performed and results 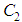 . The results of the NPCR and UACI analysis for all test images are shown in Table 8. We also present a performance comparison of [37] and [48] with our differential results in Table 8.
. The results of the NPCR and UACI analysis for all test images are shown in Table 8. We also present a performance comparison of [37] and [48] with our differential results in Table 8. 
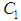 and
and 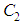 with their difference image.
with their difference image. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML