-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2016; 6(2): 25-31
doi:10.5923/j.ajsp.20160602.01

A Self-Organizing Diffusion Mobile Adaptive Network for Pursuing a Target
Amir Rastegarnia 1, Azam Khalili 1, Md Kafiul Islam 2
1Department of Electrical Engineering, University of Malayer, Malayer, Iran
2Department of Electrical and Computer Engineering, National University of Singapore, Singapore
Correspondence to: Amir Rastegarnia , Department of Electrical Engineering, University of Malayer, Malayer, Iran.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper we focus on designing self-organizing diffusion mobile adaptive networks where the individual agents are allowed to move in pursuit of an target. The well-known Adapt-then-Combine (ATC) algorithm is already available in the literature as a useful distributed diffusion-based adaptive learning network. However, in the ATC diffusion algorithm, fixed step sizes are used in the update equations for velocity vectors and location vectors. When the nodes are too far away from the target, such strategies may require large number of iterations to reach the target. To address this issue, we suggest two modifications on the ATC mobile adaptive network to improve its performance. The proposed modifications include (i) distance-based variable step size adjustment at diffusion algorithms to update velocity vectors and location vectors, (ii) to use a selective cooperation, by choosing the best nodes at every iteration, to reduce the number of communications. The performance of the proposed algorithm is evaluated by simulation tests where the obtained results show the superior performance of the proposed algorithm in comparison with the available ATC mobile adaptive network.
Keywords: Adaptive networks, Mobile networks, LMS, Sensor networks
Cite this paper: Amir Rastegarnia , Azam Khalili , Md Kafiul Islam , A Self-Organizing Diffusion Mobile Adaptive Network for Pursuing a Target, American Journal of Signal Processing, Vol. 6 No. 2, 2016, pp. 25-31. doi: 10.5923/j.ajsp.20160602.01.
Article Outline
1. Introduction
- Wireless sensor networks appear in many practical applications such as distributed sensing, intrusion detection and target localization [1-4]. In most of the aforementioned applications, nodes of a network collect data from environment and then process them collaboratively to estimate a desired parameter. Different strategies have been introduced in the literature to solve the distributed estimation problems including consensus strategies and adaptive networks [5, 6]. It has been shown in [7] that adaptive networks are more stable than consensus networks and they provide better steady-state error performance. So, in this paper we focus on adaptive network based solutions. We adopt the term adaptive networks from [8] to refer to a collection of nodes that interact with each other and function as a single adaptive entity that is able to track statistical variations of data in real-time. Two major classes of adaptive networks are incremental strategy [9-14] and diffusion strategy [15-19]. In comparison, incremental algorithms require less communication among nodes of the networks while diffusion algorithms are scalable and more robust to link and node failure [20-22]. In general, diffusion based algorithms consist of two steps including the adaptation step, where the node updates the weight estimate using local measurement data, and the combination step where the information from the neighbours are aggregated. Based on the order of these two steps, diffusion algorithms can be categorized into two classes known as the Combine-then-Adapt and Adapt-then-Combine (ATC). It is observed that the ATC version of diffusion LMS outperforms the CTA algorithm [16]. The initial diffusion adaptive networks in [15-19] did not incorporate the node mobility. In [23-26], another dimension of complexity which is node mobility has been added to the diffusion networks. The resultant mobile adaptive networks perform two diffusion-based estimation tasks: one for estimating the location of a target and the other one for tracking the center of mass of the network. Incorporating the node mobility enables the resulting diffusion networks to use them in new applications such as modelling the various forms of sophisticated behaviour exhibited by biological networks [27, 28] and source localization [29, 30].The current algorithms for mobile adaptive networks do not consider the distance to the target in their adaptation mechanisms. In other words, in the current algorithms every node in the network adjusts (updates) its velocity vector and location vector regardless of its distance to the target. When nodes are too far away from the target, such strategies may require large number of iterations to reach the target, which in turn, requires large amount of communications and computations. Thus, it is highly desirable that in a mobile adaptive network, the nodes incorporate the distance to the target information, e.g. using bigger step-sizes when they are too far from the target. To endow the ATC diffusion network with such ability, we firstly define a practical metric to describe the far field region as a region that is too far from the target. Note that the near filed is also defined as a region that includes the target. Then, according to the position of a node (inside or outside of the far field) different step size adjust mechanisms are applied. In general, as long as a node is inside the far field region, the step size parameter in update velocity vectors and location vectors are increased, whereas for a node outside of the far field the step size is iteratively reduced as it moves toward the target.Moreover, in the combination step of diffusion LMS algorithm, each node needs to gather the intermediate estimates from all of its neighbours. Thus, this step may require large amount of communications for dense networks. In some applications, however, networks cannot afford large communication overhead. To further reduce the communication load, a selective cooperation is used where every nodes selects only a subset of its niobous to share the information. The performance of the proposed algorithm is evaluated by simulation tests where the obtained results show the superior performance of the proposed algorithm in comparison with the available ATC adaptive network.Notation: We use boldface letters for matrices and vectors and small letters for scalars. The notation
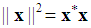 stands for the Euclidean norm of
stands for the Euclidean norm of 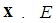 denotes the expectation operator. The set of neighbours of node
denotes the expectation operator. The set of neighbours of node 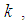 including itself, is denoted by
including itself, is denoted by 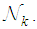
2. Mobile Adaptive Networks
- Let us consider a network with
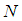 mobile nodes that are randomly distributed over a space. Let
mobile nodes that are randomly distributed over a space. Let 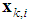 be the location of node
be the location of node 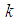 at time
at time 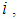 relative to some global coordinate system and
relative to some global coordinate system and 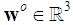 denote the location of the target. Each node
denote the location of the target. Each node 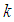 finds its neighbours within a range
finds its neighbours within a range 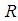 radius in each time
radius in each time 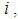 i.e.
i.e.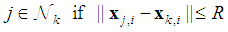 | (1) |
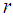 from neighbours during the motion to the target location. The distance between the target
from neighbours during the motion to the target location. The distance between the target 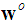 and a node
and a node 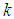 at any time
at any time 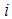 is given by (See Fig. 1)
is given by (See Fig. 1)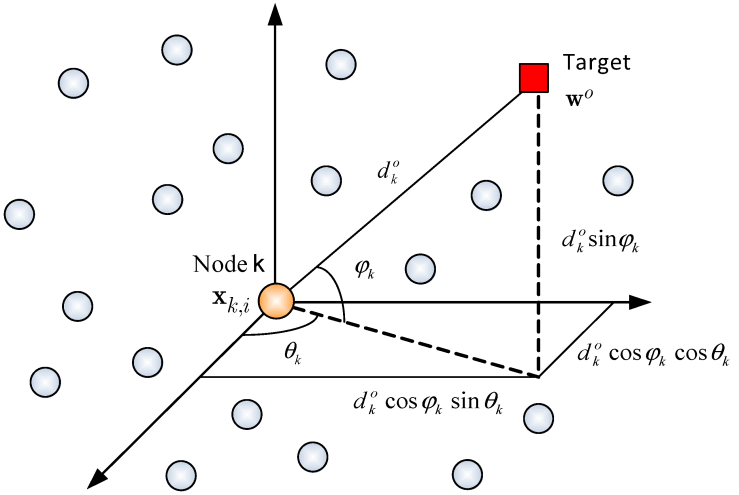 | Figure 1. Distance and direction of the target 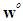 from node from node 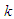 at location at location 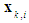 |
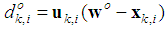 | (2) |
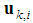 denotes the direction of the target including the azimuth angle
denotes the direction of the target including the azimuth angle 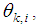 and the elevation angle
and the elevation angle 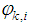 which is given as
which is given as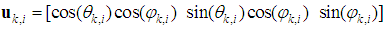 | (3) |
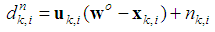 | (4) |
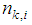 denotes the noise term which is assumed to be zero-mean Gaussian noise. Intuitively, the noise variance,
denotes the noise term which is assumed to be zero-mean Gaussian noise. Intuitively, the noise variance, 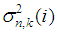 can follow a relation such as
can follow a relation such as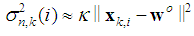 | (5) |
 as [23]. Note that (5) is reasonable since we usually assume the signal power to decrease in proportional to the square of the propagation distance. We can rewrite the above equation as [23, 25]
as [23]. Note that (5) is reasonable since we usually assume the signal power to decrease in proportional to the square of the propagation distance. We can rewrite the above equation as [23, 25]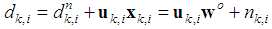 | (6) |
 every node
every node  has access to local data
has access to local data  and the local data from its neighbours. Using these data every node estimates the position of the target at
and the local data from its neighbours. Using these data every node estimates the position of the target at 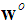 which can be achieved by solving the following optimization problem
which can be achieved by solving the following optimization problem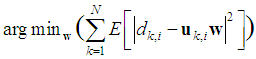 | (7) |
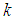 uses its own data to update the weight estimate
uses its own data to update the weight estimate 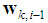 to intermediate value
to intermediate value 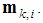 In the combination step each node gathers the intermediate estimates
In the combination step each node gathers the intermediate estimates 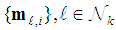 combines them to obtain the updated weight estimate
combines them to obtain the updated weight estimate 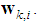 The algorithm is described as follows:
The algorithm is described as follows: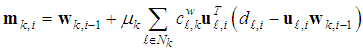 | (8) |
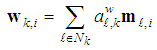 | (9) |
 is the learning step size. The two sets of non-negative real coefficients
is the learning step size. The two sets of non-negative real coefficients 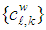 and
and 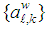 satisfy
satisfy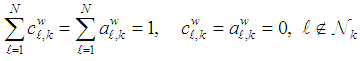 | (10) |
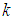 can update its location as
can update its location as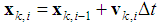 | (11) |
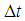 is the time step and
is the time step and 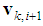 denoted the velocity of the node
denoted the velocity of the node 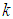 . Every node adjusts its velocity vector according to the following expression [23]
. Every node adjusts its velocity vector according to the following expression [23]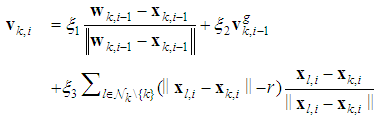 | (12) |
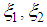 and
and 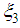 are non-negative weighting factors, and
are non-negative weighting factors, and 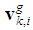 is the local estimate for the global velocity of the center of gravity of the network which is designed to allow for coherent motion. To use (12) each node needs to estimate
is the local estimate for the global velocity of the center of gravity of the network which is designed to allow for coherent motion. To use (12) each node needs to estimate 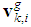 in a distributed way. Since the velocities of nodes are changing in time, we need to keep track of
in a distributed way. Since the velocities of nodes are changing in time, we need to keep track of 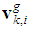 over time. So we introduce the global cost function as follows
over time. So we introduce the global cost function as follows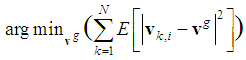 | (13) |
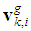
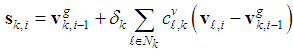 | (14) |
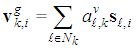 | (15) |
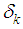 is a positive step size and
is a positive step size and 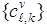 and
and 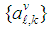 are two sets of non-negative real coefficients satisfying the same properties as (10).
are two sets of non-negative real coefficients satisfying the same properties as (10).3. Proposed Algorithm
3.1. Motivation for Current Work
- In the existing algorithms for adaptive mobile networks, there is no specific strategy for going faster toward the target. In other words, in the existing algorithms although the algorithm is designed in such a way that the set of nodes can move towards the goal harmoniously, but they do not consider the distance to the target in their velocity and location update equations. To address this issue, instead of using fixed learning parameter
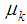 in (8), we use variable step-size parameter which has the following conditions● if node
in (8), we use variable step-size parameter which has the following conditions● if node 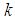 at iteration
at iteration 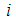 is too far from the target,
is too far from the target, 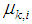 should be increased. Note that to prevent algorithm divergence and movement control of the set of nodes, we have to select the upper limit for step-size parameters.● if distance of node
should be increased. Note that to prevent algorithm divergence and movement control of the set of nodes, we have to select the upper limit for step-size parameters.● if distance of node 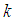 at iteration
at iteration 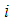 becomes less than a predefined value,
becomes less than a predefined value, 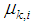 should be iteratively decreased as nodes approach the target. In this case we consider a lower bound for
should be iteratively decreased as nodes approach the target. In this case we consider a lower bound for 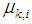 to avoid slow convergence rate.
to avoid slow convergence rate.3.2. Algorithm Development
- To begin with, we define the far field region as follows.Definition 1: By far field, we mean a region
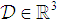 that the nodes inside it are far from the target, or
that the nodes inside it are far from the target, or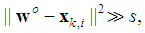 | (16) |
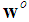 which is not available. To have a practical metric, we use
which is not available. To have a practical metric, we use 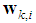 as an estimate of
as an estimate of 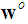 at iteration
at iteration 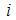 and rewrite (16) as
and rewrite (16) as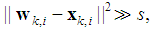 | (17) |
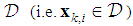 a bigger step-size in the update equation is required to move in the direction of
a bigger step-size in the update equation is required to move in the direction of 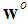 . So we replace
. So we replace 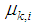 in (8) as follows
in (8) as follows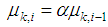 | (18) |
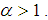 Obviously, in this case we have
Obviously, in this case we have 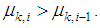 It should be noted that according to the recursive equation in (8), increasing the step size may lead to algorithm divergence. So, in order to avoid algorithm divergence we consider an upper bound for step sizes as
It should be noted that according to the recursive equation in (8), increasing the step size may lead to algorithm divergence. So, in order to avoid algorithm divergence we consider an upper bound for step sizes as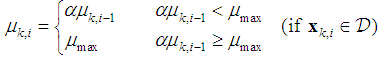 | (19) |
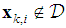 we need to reduce the step size as nodes moves toward the target at
we need to reduce the step size as nodes moves toward the target at 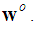 In this case the step size adaptation function can be given by
In this case the step size adaptation function can be given by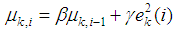 | (20) |
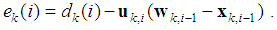 In this case
In this case 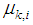 becomes smaller as node approaches the target. To avoid slow convergence rate, we can consider a lower bound for step size as follows
becomes smaller as node approaches the target. To avoid slow convergence rate, we can consider a lower bound for step size as follows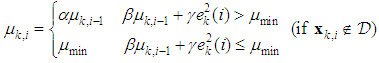 | (21) |
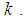 To this end, we select neighbours of node
To this end, we select neighbours of node 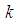 that have small estimated variance product measure and ignore the other neighbours. One way is to change (1) as
that have small estimated variance product measure and ignore the other neighbours. One way is to change (1) as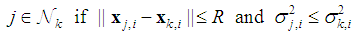 | (22) |
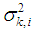 which are unknown in general and for practical usage they must be estimated. At every node
which are unknown in general and for practical usage they must be estimated. At every node 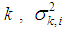 can be estimated by time-averaging as
can be estimated by time-averaging as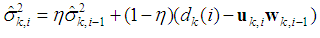 | (23) |
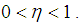 Finally, using the introduced modifications we arrive at the proposed algorithm as given in the Table. 1.
Finally, using the introduced modifications we arrive at the proposed algorithm as given in the Table. 1.
|
4. Simulation Results
- In this section we present simulation results to evaluate the performance of our proposed algorithm. We use a network with
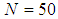 nodes that are initially uniformly distributed inside a cube with length 10. Their velocities are set at random directions and unit magnitude. The simulation parameters are set as follows. The factors of velocity control are
nodes that are initially uniformly distributed inside a cube with length 10. Their velocities are set at random directions and unit magnitude. The simulation parameters are set as follows. The factors of velocity control are 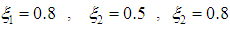 . We further set
. We further set 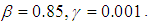 The combination coefficients are set as
The combination coefficients are set as 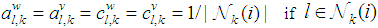 . We set the time duration to
. We set the time duration to 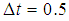 and
and 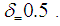 Moreover, optimal distance between two neighbours is set to
Moreover, optimal distance between two neighbours is set to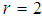 . A node chooses nearest neighbours from neighbours within the radius
. A node chooses nearest neighbours from neighbours within the radius 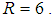 The observation noise
The observation noise 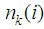 is assumed to be zero-mean Gaussian noise which is given by (5).Fig. 2 shows the network transient mean-square deviation (MSD) (for two different algorithms) which is defined as
is assumed to be zero-mean Gaussian noise which is given by (5).Fig. 2 shows the network transient mean-square deviation (MSD) (for two different algorithms) which is defined as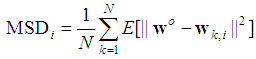 | (24) |
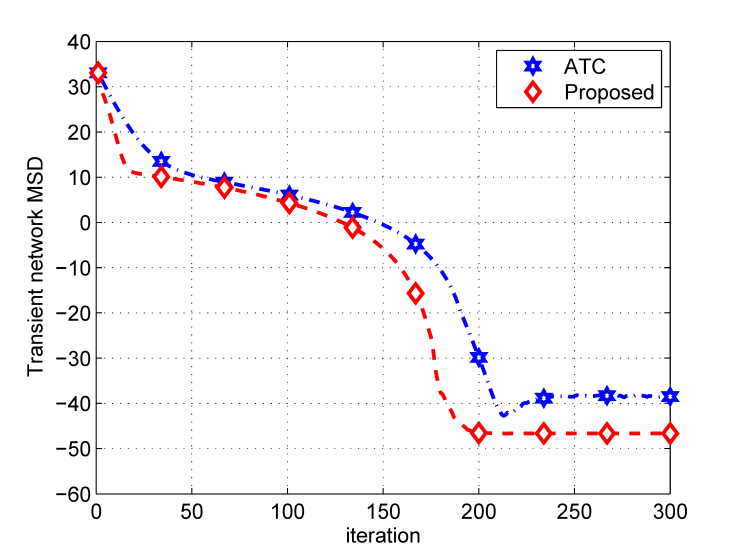 | Figure 2. Transient network MSD for estimating the target location at 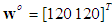 |
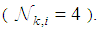 Moreover, each node uses fixed step-size
Moreover, each node uses fixed step-size 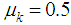 at every iteration. Fig. 2 shows the transient network MSD for estimating the target location at
at every iteration. Fig. 2 shows the transient network MSD for estimating the target location at 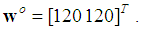 These curves are averaged over 50 experiments with the same initial state of
These curves are averaged over 50 experiments with the same initial state of 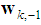 for all
for all 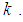 We observe that for both algorithms the transient MSD decreases dramatically in the first phase, then the network moves towards the target and finally, at steady state, the network arrives at the target. However, the proposed algorithm provides better performance compared to the ATC diffusion algorithm. Fig. 3 illustrates the maneuver of a mobile network (with ATC and proposed algorithms) over time.
We observe that for both algorithms the transient MSD decreases dramatically in the first phase, then the network moves towards the target and finally, at steady state, the network arrives at the target. However, the proposed algorithm provides better performance compared to the ATC diffusion algorithm. Fig. 3 illustrates the maneuver of a mobile network (with ATC and proposed algorithms) over time. 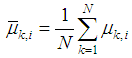 evolves over time. We can see that at the first iteration since the nodes are too far from the target, at every node the step size parameter has been increased iteratively so that after some iterations we have
evolves over time. We can see that at the first iteration since the nodes are too far from the target, at every node the step size parameter has been increased iteratively so that after some iterations we have 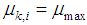 . As the nodes move toward the target, at every node the step size parameter has been decreased iteratively.
. As the nodes move toward the target, at every node the step size parameter has been decreased iteratively.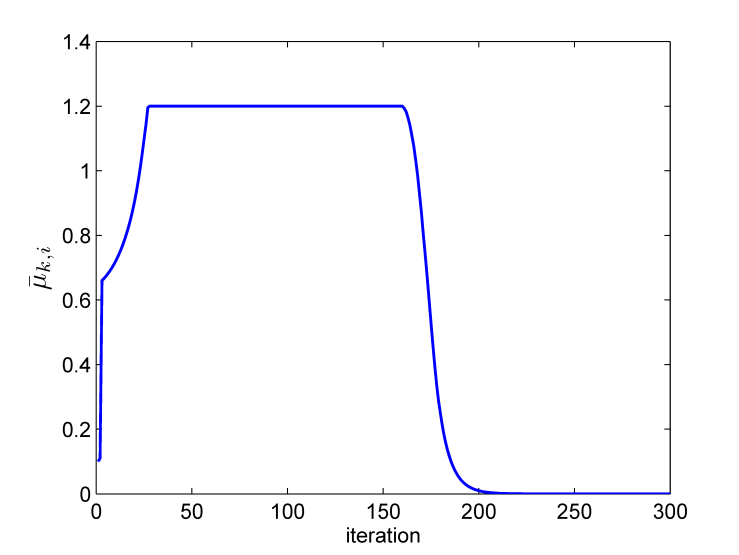 | Figure 4. The network average step size  over iteration over iteration |
 (according to our simulation setup) while the proposed algorithm uses small number of neighbours which means it requires less communication load.
(according to our simulation setup) while the proposed algorithm uses small number of neighbours which means it requires less communication load.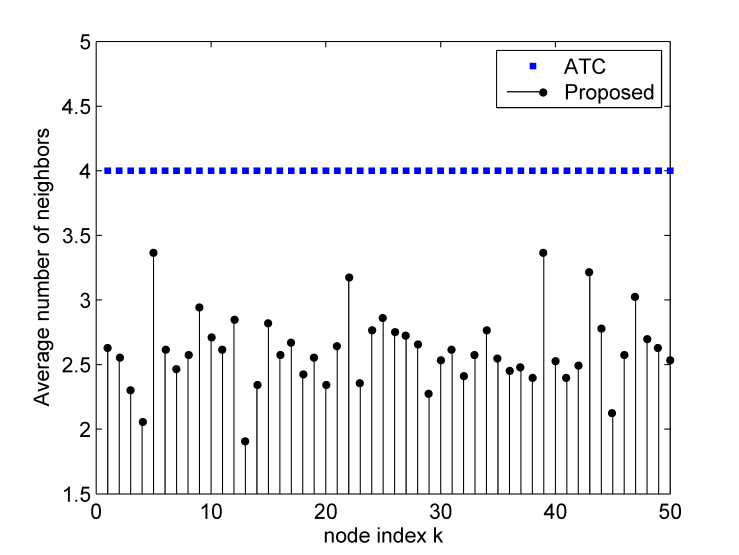 | Figure 5. The average number of neighbours for every node |
5. Conclusions
- In this paper we proposed a modified ATC diffusion algorithm for mobile adaptive networks where the individual agents are allowed to move in pursuit of a target. The motivation was that in the ATC algorithm fixed step sizes are used in the update equations for velocity vectors and location vectors. When the nodes are too far away from the target, such strategies may require large number of iterations to reach the target. To address this issue, in the proposed algorithm we used distance-based variable step sizes for adjustment at diffusion algorithms to update velocity vectors and location vectors. We also used a selective cooperation where only a subset of nodes at each iteration is used to share information. The performance of the proposed algorithm was evaluated by simulation tests where the obtained results showed the superior performance of the proposed algorithm in comparison with the available ATC mobile adaptive network. In our future work we will develop diffusion mobile adaptive network for pursuing multiple targets.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
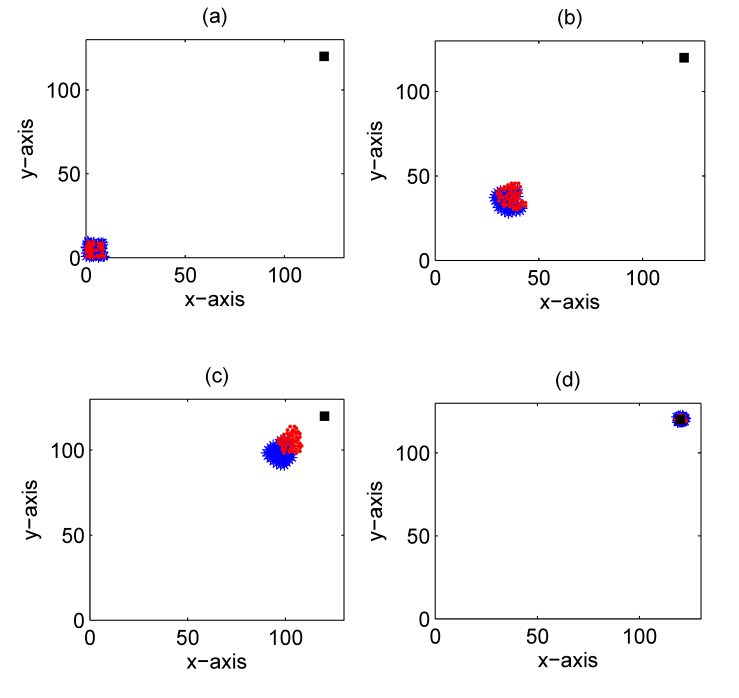
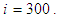 Note that
Note that 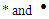 indicates the locations and moving directions of the nodes with ATC, proposed algorithm respectively and
indicates the locations and moving directions of the nodes with ATC, proposed algorithm respectively and  denotes the location of the target
denotes the location of the target