-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2016; 6(1): 1-13
doi:10.5923/j.ajsp.20160601.01

Chaos-Based Image Encryption Using an Improved Quadratic Chaotic Map
Noha Ramadan 1, Hossam Eldin H. Ahmed 1, Said E. Elkhamy 2, Fathi E. Abd El-Samie 1
1Communication, Faculty of Electronic Engineering, Menofia University, Egypt
2Electrical Engineering, Faculty of Engineering, Alexandria University, Egypt
Correspondence to: Noha Ramadan , Communication, Faculty of Electronic Engineering, Menofia University, Egypt.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In recent years, chaos-based image encryption has become an efficient way to encrypt images due to its high security. In this paper, we improve the classical Quadratic chaotic map to enhance its chaotic properties and use it for image encryption. Compared with the classical Quadratic map, the proposed Quadratic map demonstrates better chaotic properties for encryption such as a much larger maximal Lyapunov exponent. The proposed image encryption scheme is based on two chaotic maps. The first map is the Chepyshev chaotic map, which is used for the permutation of the pixels of the image. The permuted image is subjected to the diffusion process using the improved Quadratic map in an efficient encryption algorithm which its key is related to the original image. The main advantages of the proposed scheme are the large key space and its resistance to various attacks. Simulation results show that the proposed scheme has a high security level with low computational complexity, which makes it suitable for real-time applications.
Keywords: Chaos encryption, Quadratic map, Chepyshev, Lyapunov exponent
Cite this paper: Noha Ramadan , Hossam Eldin H. Ahmed , Said E. Elkhamy , Fathi E. Abd El-Samie , Chaos-Based Image Encryption Using an Improved Quadratic Chaotic Map, American Journal of Signal Processing, Vol. 6 No. 1, 2016, pp. 1-13. doi: 10.5923/j.ajsp.20160601.01.
Article Outline
1. Introduction
- In recent years, the transmission of a large amount of data such as video conferences, medical and military images over communication media was highly developed. The security of information transmitted is a vital issue. Most conventional secure ciphers such as Data Encryption Standard (DES) [1] and Advanced Encryption Standard (AES) [2] are not suitable for fast encryption of a large data volume in real time. The implementation of traditional algorithms for image encryption is even more complicated because of the high correlation between image pixels. Therefore, there is still a lot of work to be done for the development of sophisticated encryption methods. Many researchers have pointed out the existence of a strong relationship between chaos and cryptography. The idea of using chaos in cryptography can be traced back to Shannon on secrecy systems [3]. Although the word "chaos" was not minted till the 1970s [4], the use of chaos in cryptography seems quite natural. The two basic properties of a good cipher; confusion and diffusion are strongly related to the fundamental characteristics of chaos such as a broadband spectrum, ergodicity and high sensitivity to initial conditions. The implementation of Shannon's idea had to wait till the development of chaos theory in the 1980s. In the first scientific paper on chaotic cryptography that appeared in 1989, Matthews [5] came up with the idea of a stream cipher based on one-dimensional chaotic map. Afterwards, chaotic cryptography has spread and more papers about digital chaotic ciphers have been published [6-8].Traditionally, encryption is based on discrete number theory, so that data has to be digitized before any encryption process can take place. In order to encrypt a continuous voice or a video in the old fashion, digitalization and encryption can pose a heavy computational process. The use of chaotic communication enables to encrypt the message waveform without a need to digitalize it [9].Based on strengths and weaknesses of already existing algorithms, Kelber and Schwarz formulated several general rules to design a good chaos-based cryptosystem [9-10]:• Either use a suitable chaotic map, which preserves important properties during discretization for block cipher or use a balanced combining function and a suitable key-stream generator for a stream cipher.• Use a large key space.• Avoid simple permutations of identical system parameters.• Use the same precision for sub-key values and their corresponding system parameters.• Use a complex input key transformation.• Use a dynamical system.• Use complex nonlinearities.• Modify nonlinearities in terms of key and signal values.• Use several rounds of operation for block ciphers.The basic properties of chaotic systems are the deterministicity, the sensitivity to initial conditions and parameters and the ergodicity. Deterministicity means that chaotic systems have some determining mathematical equations ruling their behavior. The sensitivity to initial conditions means that when a chaotic map is iteratively applied to two initially close points, the iterations quickly diverge, and become uncorrelated in the long term. Sensitivity to parameters causes the properties of the map to change quickly, when slightly disturbing the parameters, on which the map depends. Hence, a chaotic system can be used as a pseudo-random number generator. The ergodicity property of a chaotic map means that if the state space is partitioned into a finite number of regions, no matter how many, any orbit of the map will pass through all these regions. A number of traditional chaotic maps such as Quadratic map [11] and Logistic map [12] have limited properties and may no longer satisfy our needs. Without improvement of chaotic maps, our applications will remain unchanged and might be subject to different attacks in the future. Hence, there is a bad need for more improvements in the chaotic maps.In this paper, an improved Quadratic chaotic map is first introduced. We use the maximal Lyapunov exponent [13] and the bifurcation diagram to determine the performance of the map. A new image encryption scheme based on this improved Quadratic map is presented containing two main processes; permutation and diffusion. The permutation process breaks the strong relationship between adjacent pixels. The permutation operation only shuffles the pixel positions without changing values. The shuffled and original images have the same entropy, and therefore the shuffled image is weak against statistical attack and known plain-text attack. In the diffusion process, the pixel values are altered. Most researchers focus on security improvements [14-15], while only a few are dealing with efficiency issues [16-17]. For most of the security improvements, researchers need at least three rounds of the diffusion process to obtain a satisfactory performance. Researchers focusing on efficiency improvement only need one round of the diffusion process to achieve the high security level and speed up the performance. However, some of the proposed algorithms lead to a longer processing time in a single round. Therefore, the key problem of designing an efficient image cryptosystem is how to reduce the computational complexity with efficiently to avoid the large number of rounds in the generation of diffusion and permutation keys and then achieve high speed performance. At the permutation step, we sort the chaotic sequences of the Chepyshev map in order to shuffle the entire image. At the diffusion step, the shuffled image is encrypted with a key related to plain image.
2. Analysis of Quadratic Map
- Quadratic map is a basic example of a chaotic system. The equation of the classical Quadratic map is [18]:
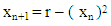 | (1) |
2.1. Iteration Property
- The iteration diagram plots the relation between the number of iterations n and the Quadratic chaotic map at different values of the chaotic parameter r and at a specific initial value x0. The parameter r can be divided into three regions, which can be examined by simulation using MATLAB as following: When
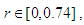 as shown in Fig. 1 (a), the calculated value come to the same result after several iterations without any chaotic behavior. When
as shown in Fig. 1 (a), the calculated value come to the same result after several iterations without any chaotic behavior. When 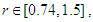 as shown in Fig. 1 (b), the system appears as having a periodic behavior. When
as shown in Fig. 1 (b), the system appears as having a periodic behavior. When 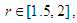 it becomes a chaotic system as shown in Fig. 1 (c).
it becomes a chaotic system as shown in Fig. 1 (c).2.2. Bifurcation Diagram
- Bifurcation is usually referred to as the qualitative transition from regular to chaotic behavior by changing the control parameter. The bifurcation diagram is used to study the chaotic system as a function of the values of the control parameters. This diagram allows knowing the regions of the system displaying convergence, bifurcation, and chaos depending on the values of the control parameters [19].Fig. 1 (d) shows the bifurcation diagram of the classical Quadratic map. This diagram has three regions. The convergence region is at
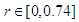 . The bifurcation region is at
. The bifurcation region is at 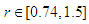 . The chaos region is at
. The chaos region is at 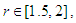 where the chaotic behavior occurs.
where the chaotic behavior occurs.2.3. Lyapunov Exponent
- Lyapunov exponent
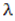 represents the features of a chaotic system and can largely express the overall performance of chaotic maps. It is used as a quantitative measure for the sensitive dependence on initial conditions. For a discrete system xn+1 =f(xn) and for an orbit starting with x0, the Lyapunov exponent can be defined as follows [20-21]:
represents the features of a chaotic system and can largely express the overall performance of chaotic maps. It is used as a quantitative measure for the sensitive dependence on initial conditions. For a discrete system xn+1 =f(xn) and for an orbit starting with x0, the Lyapunov exponent can be defined as follows [20-21]: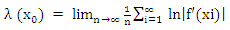 | (2) |
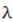 defined by Eq.(2) as the Maximal Lyapunov Exponent (MLE), because it determines a notion of predictability for a chaotic system. The larger MLE is, the more chaotic the map is and the smaller the number of iterations necessary to achieve the required degree of diffusion or confusion of information is, and this means a better chaotic map.Fig. 1 (e) shows the Lyapunov exponent of the classical Quadratic map. It is obviously clear that when
defined by Eq.(2) as the Maximal Lyapunov Exponent (MLE), because it determines a notion of predictability for a chaotic system. The larger MLE is, the more chaotic the map is and the smaller the number of iterations necessary to achieve the required degree of diffusion or confusion of information is, and this means a better chaotic map.Fig. 1 (e) shows the Lyapunov exponent of the classical Quadratic map. It is obviously clear that when 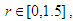 all Lyapunov exponents are less than or equal to zero. When
all Lyapunov exponents are less than or equal to zero. When 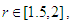 the Lyapunov exponents are positive, and hence chaotic. The maximal Lyapunov exponent of the Quadratic map is 0.6720.
the Lyapunov exponents are positive, and hence chaotic. The maximal Lyapunov exponent of the Quadratic map is 0.6720.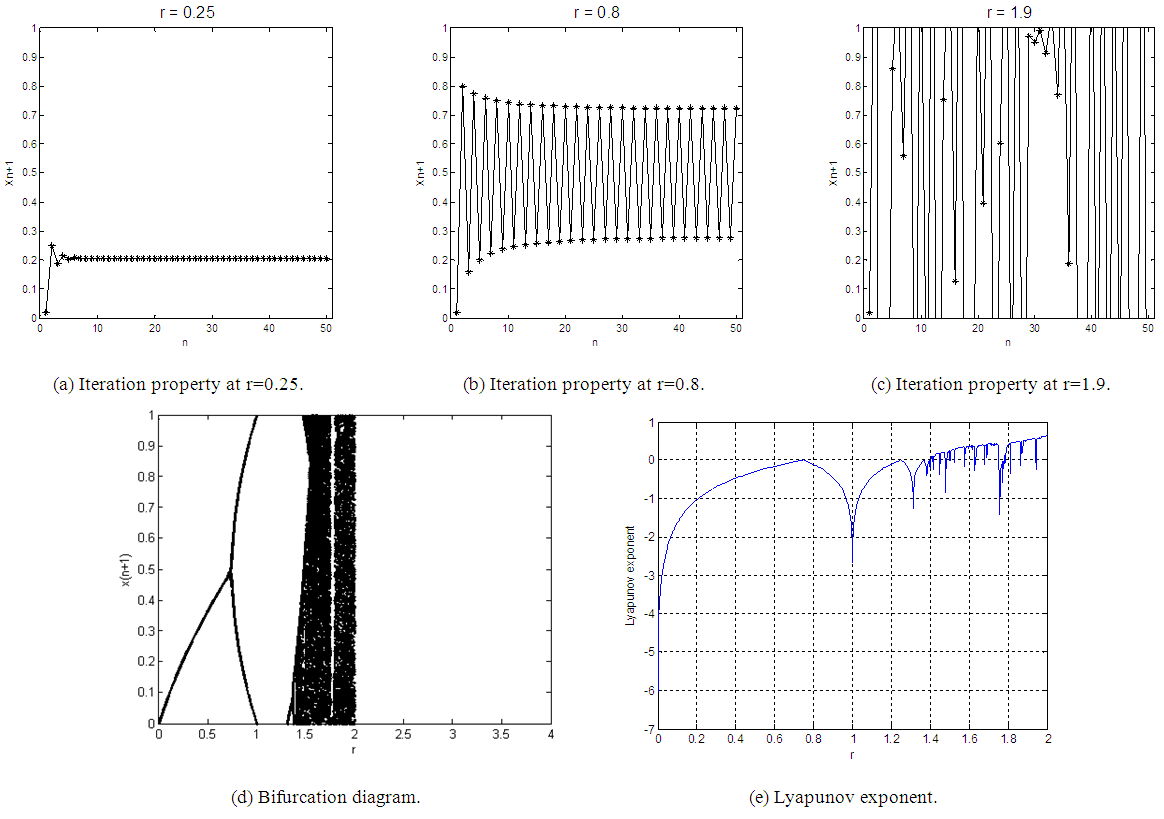 | Figure 1. Analysis of the classical Quadratic map at x0=0.02 |
3. The Proposed Quadratic Map
- The equation of the proposed quadratic map is:
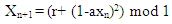 | (3) |
3.1. Analysis of the Proposed Quadratic Map 1
- The equation of the proposed Quadratic map 1 at a= 2 is:
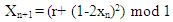 | (4) |
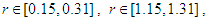 etc…. to infinity. The convergence regions are at
etc…. to infinity. The convergence regions are at 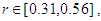
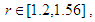 etc…. to infinity. The chaos regions are at
etc…. to infinity. The chaos regions are at 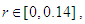
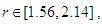
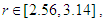 etc…. to infinity, where the chaotic behavior occurs.Now, it is obvious that the chaotic range of the proposed Quadratic map 1 is larger than the chaotic range for the classical one, and hence this will increase the available chaotic value of parameter r that can be used in encryption.In Fig. 2 (e), the Lyapunov exponent
etc…. to infinity, where the chaotic behavior occurs.Now, it is obvious that the chaotic range of the proposed Quadratic map 1 is larger than the chaotic range for the classical one, and hence this will increase the available chaotic value of parameter r that can be used in encryption.In Fig. 2 (e), the Lyapunov exponent 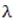 has a positive value at
has a positive value at 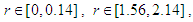
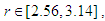 etc…, and hence the proposed Quadratic map 1 exhibits a chaotic behavior at these periods. The MLE of the proposed Quadratic map 1 is 0.6732, which is greater than the classical Quadratic map but still small.
etc…, and hence the proposed Quadratic map 1 exhibits a chaotic behavior at these periods. The MLE of the proposed Quadratic map 1 is 0.6732, which is greater than the classical Quadratic map but still small.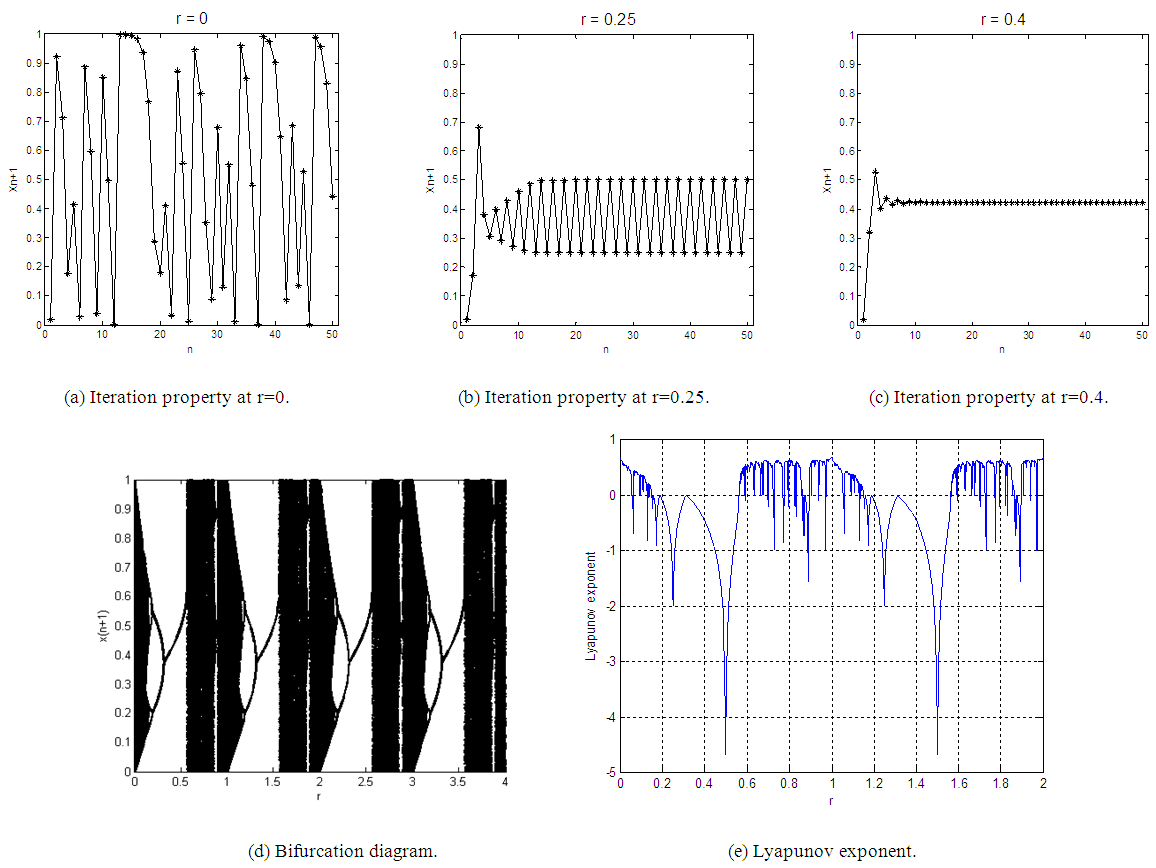 | Figure 2. Analysis of the proposed Quadratic map 1 at x0=0.02 |
3.2. Analysis of the Proposed Quadratic Map 2
- The equation of the proposed Quadratic map 2 at a= 4 is:
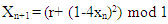 | (5) |
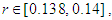
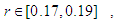
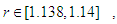
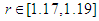 etc…. to infinity. The convergence regions are at
etc…. to infinity. The convergence regions are at 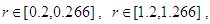 etc…. to infinity. The chaos regions are at
etc…. to infinity. The chaos regions are at 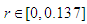 ,
, 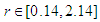 ,
, 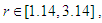 etc…. to infinity, except the small regions of convergence and bifurcation, where the chaotic behavior occurs.In Fig. 3 (e), the Lyapunov exponent
etc…. to infinity, except the small regions of convergence and bifurcation, where the chaotic behavior occurs.In Fig. 3 (e), the Lyapunov exponent 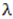 has a positive value at all values of r except small ranges of convergence and bifurcation. Hence, the proposed Quadratic map 2 exhibits a chaotic behavior in the rest of the range. The MLE of the proposed Quadratic map 2 is 2.0257, which is much greater than the classical Quadratic map and proposed Quadratic map 1.
has a positive value at all values of r except small ranges of convergence and bifurcation. Hence, the proposed Quadratic map 2 exhibits a chaotic behavior in the rest of the range. The MLE of the proposed Quadratic map 2 is 2.0257, which is much greater than the classical Quadratic map and proposed Quadratic map 1.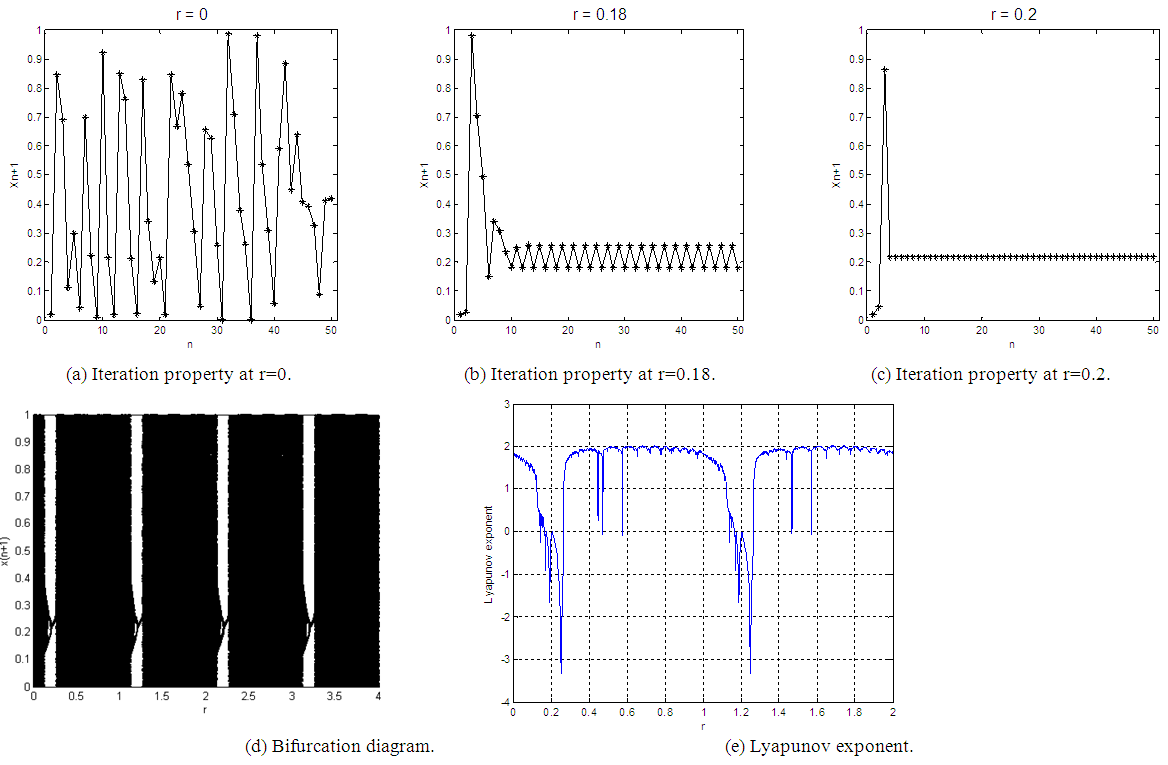 | Figure 3. Analysis of the proposed Quadratic map 2 at x0=0.02 |
3.3. Analysis of the Proposed Quadratic Map 3
- The equation of the proposed Quadratic map 3 at a= 8 is:
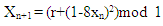 | (6) |
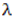 has a positive value at all values of r except the values of 0.11, 1.11, etc…. So, the proposed Quadratic map 3 exhibits a chaotic behavior at the rest of the range. The MLE of the proposed Quadratic map 3 is 3.4709, which is much greater than the classical Quadratic map and the proposed Quadratic map 1 and 2.
has a positive value at all values of r except the values of 0.11, 1.11, etc…. So, the proposed Quadratic map 3 exhibits a chaotic behavior at the rest of the range. The MLE of the proposed Quadratic map 3 is 3.4709, which is much greater than the classical Quadratic map and the proposed Quadratic map 1 and 2.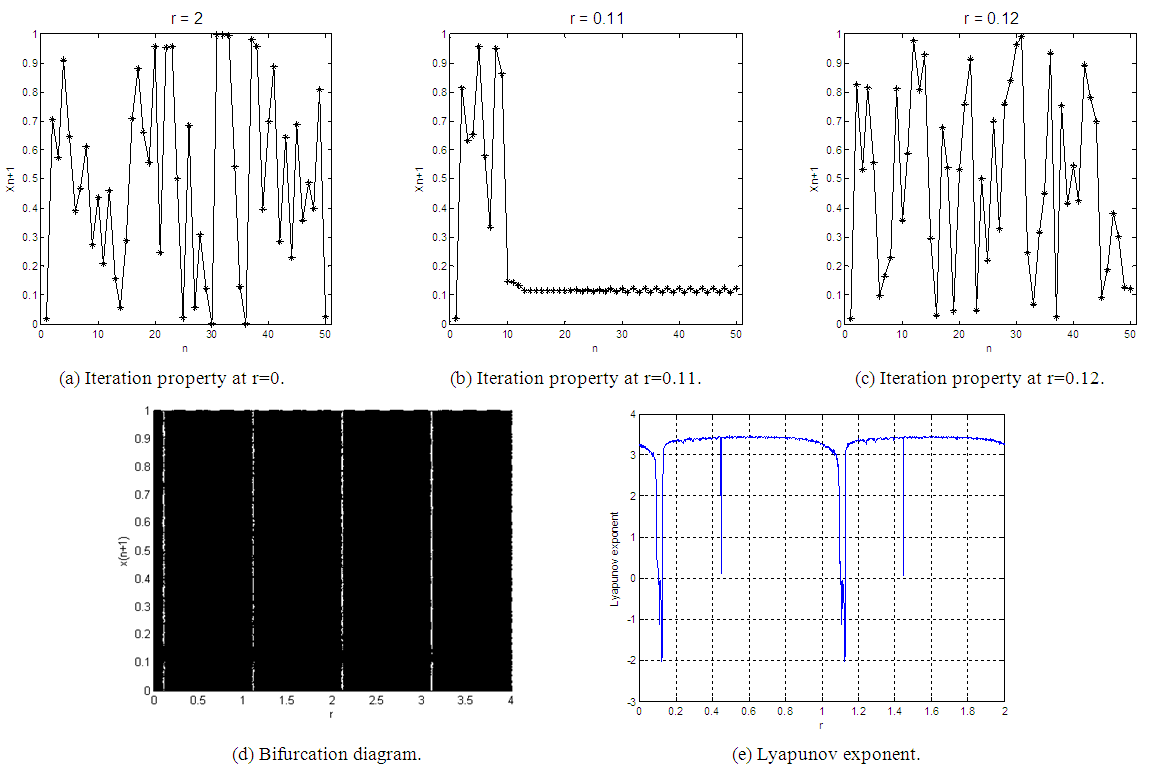 | Figure 4. Analysis of the proposed Quadratic map 3 at x0=0.02 |
 | Table (1). Comparison between the classical and proposed Quadratic maps |
4. Application on Image Encryption
- Now, we will introduce the proposed image encryption scheme based on two chaotic maps; the Chepyshev map and the proposed Quadratic maps we have just constructed.
4.1. Chepyshev Chaotic Map
- The Chepyshev chaotic map is a one dimensional chaotic system with one initial condition x0 and one control parameter k and can be described as follows [22]:
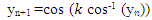 | (7) |
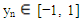 for n = 0, 1,2, … and
for n = 0, 1,2, … and 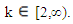 The bifurcation diagram of the Chepyshev map in Fig. 4 shows that all the (y0, k) where
The bifurcation diagram of the Chepyshev map in Fig. 4 shows that all the (y0, k) where 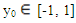 and 2 ≤ k < ∞ can be used as secret keys. The Chepyshev map has a positive increasing Lyapunov exponent at k >= 2, and thus, it is always chaotic as shown in Fig. 5.
and 2 ≤ k < ∞ can be used as secret keys. The Chepyshev map has a positive increasing Lyapunov exponent at k >= 2, and thus, it is always chaotic as shown in Fig. 5. 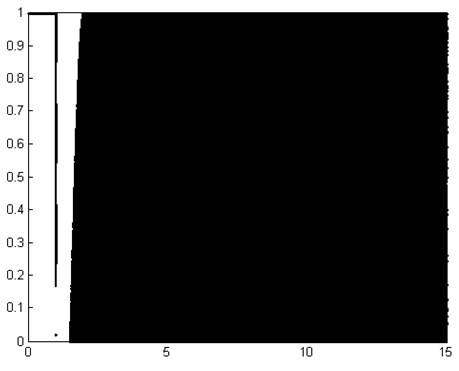 | Figure 4. Bifurcation diagram of the Chepyshev chaotic map at x0=0.02 |
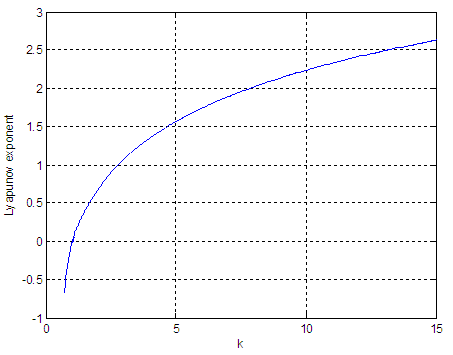 | Figure 5. Lyapunov exponent of the Chepyshev chaotic map |
4.2. The Permutation Process
- We use Chepyshev chaotic map to generate chaotic sequences x and then sort that chaotic numbers in ascending or descending order for the generation of the permutation key. For a 256-level gray-scale image, y0= 0.97 and k= 2.995. We sort the chaotic sequences in the index matrix used in shuffling the original image to obtain the permuted image. The original Cameraman image and the permuted image after permutation are shown in Fig. 7 and Fig. 8. After obtaining the shuffled image, the correlation among the adjacent pixels is completely disturbed and the image is completely unrecognizable. The histogram of the permuted image and the original image are the same, since there is no change in the intensity of pixels as shown in Fig. 9 and Fig. 10. Therefore, the permuted image is weak against statistical attack, and known plain-text attack. As a result, we employ a diffusion process after permutation to improve the security.
 | Figure 7. Original image |
 | Figure 8. Permuted image |
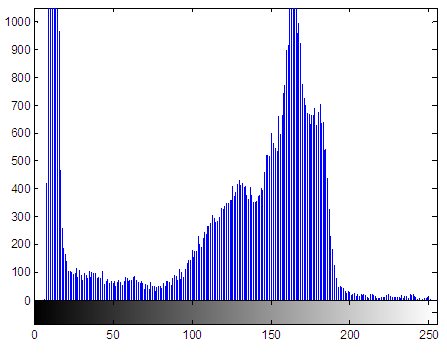 | Figure 9. Histogram of the original image |
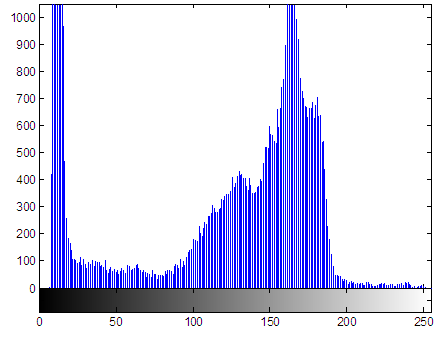 | Figure 10. Histogram of the permuted image |
4.3. Image Diffusion Based on the Proposed Quadratic Chaotic Maps
- The diffusion step in the proposed encryption scheme is performed by the key related to the plain image algorithm which used only one round diffusion operation and its key depends on the initial key and the original image [23]. We will use the proposed Quadratic maps and also the classical Quadratic map in the diffusion process and compare between them. After comparison, we will get the chaotic map which has the best performance. We will treat the image as a one dimensional vector im = {im1, im2… imL} of length L= M×N. The initial value x0 =0.02. We will discuss the encryption process only, because the decryption is the reverse process. The details of the encryption process can be summarized as follows:Step 1: for n =1, iterate the classical and proposed Quadratic maps using Eqs. (1), (4), (5) and (6) for only one time to get x1.Step 2: modify x1 according to the following equation, where im1 is any arbitrary image pixel.
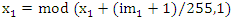 | (8) |
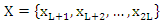 | (9) |
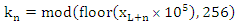 | (10) |
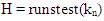 | (11) |
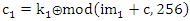 | (12) |
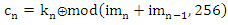 | (13) |
5. The Proposed Scheme
- The proposed encryption scheme is based on a permutation-diffusion architecture. The first stage is applying the permutation process to the original image. Then, the permuted image is subjected to the diffusion process. The permutation is achieved using Chepyshev map. The diffusion process is achieved by the key related to the plain image algorithm based on the proposed Quadratic maps we have just constructed. The decryption process is simply the reverse of the encryption process. See Fig. 11.
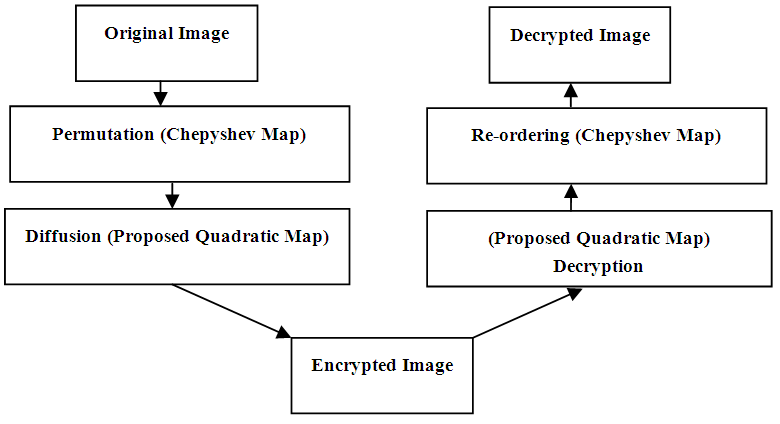 | Figure 11. The proposed scheme |
6. Performance Analysis
- The quality of the encryption algorithm is its ability to resist different kinds of known attacks such as known/chosen plain-text attack, cipher-text only attack, statistical attack, differential attack, and various brute-force attacks. We will examine the proposed algorithm by measuring security, statistical, and sensitivity analysis on different images.
6.1. Security Analysis
6.1.1. Key Space Analysis
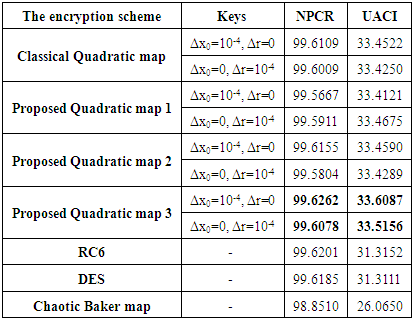
- The key space is the total number of different keys that can be used in the encryption process. The proposed algorithm consists of two processes; permutation and diffusion. In the permutation process, we use Chepyshev map with two independent variables y0 and k. In the diffusion process, the Quadratic map has two independent variables x0 and r. In the key related to the plain text algorithm, we have a constant integer c and c
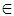 [1, 255]. As a result, the key space is {y0, k, x0, r, c}. Since y0, k, x0 and r are double precision numbers, the total number of different values for y0, k, x0 and r is more than 1014. So, the key space is larger than 1014
[1, 255]. As a result, the key space is {y0, k, x0, r, c}. Since y0, k, x0 and r are double precision numbers, the total number of different values for y0, k, x0 and r is more than 1014. So, the key space is larger than 1014 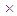 1014
1014 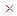 1014
1014  1014
1014  255. This large key space is enough to resist brute-force attack. On the other hand, the key space of RC6, DES and chaotic Baker map for the same 256 level gray-scale image is 2128, 256, and 263 respectively [24]. See Table (2)
255. This large key space is enough to resist brute-force attack. On the other hand, the key space of RC6, DES and chaotic Baker map for the same 256 level gray-scale image is 2128, 256, and 263 respectively [24]. See Table (2)
|
6.1.2. Statistical Analysis
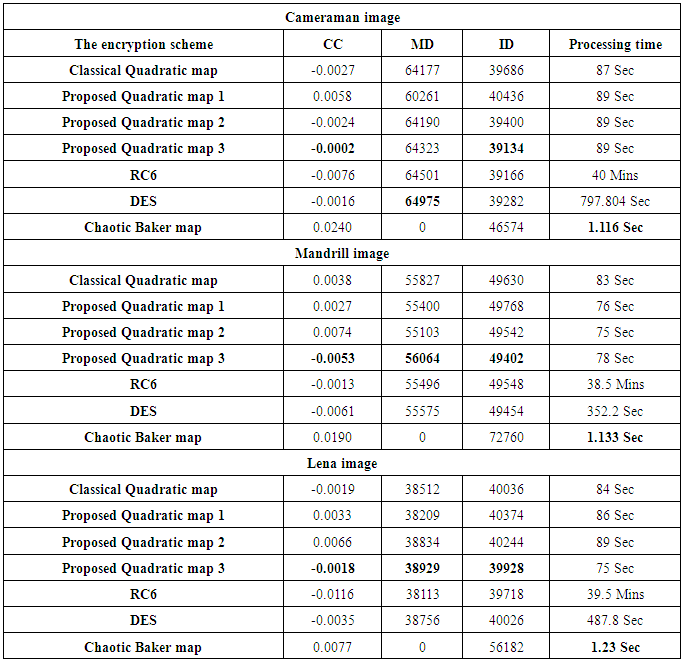
- In order to prove the security of the proposed encryption algorithm, the following statistical tests are performed.(a) HistogramHistogram clarifies that how pixels in an image are distributed by plotting the number of pixels at each gray-scale level. The histogram of the original Cameraman, Mandrill and Lena images and their encrypted versions with the classical Quadratic map, the proposed Quadratic map 1, 2 and 3 are shown in Figs. 12, 13 and 14. These figures show that the histograms of the encrypted images of all Quadratic maps are fairly uniform and completely different from those of the original images.
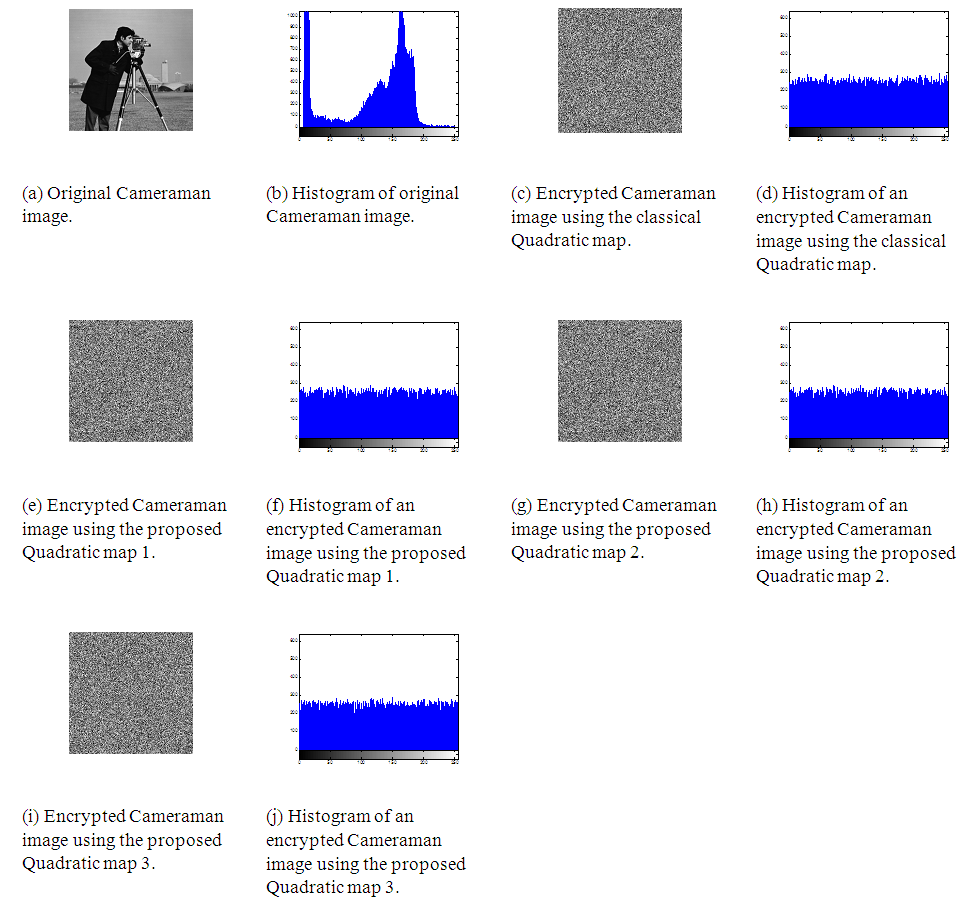 | Figure 12. Cameraman image encryption with the classical and proposed Quadratic maps |
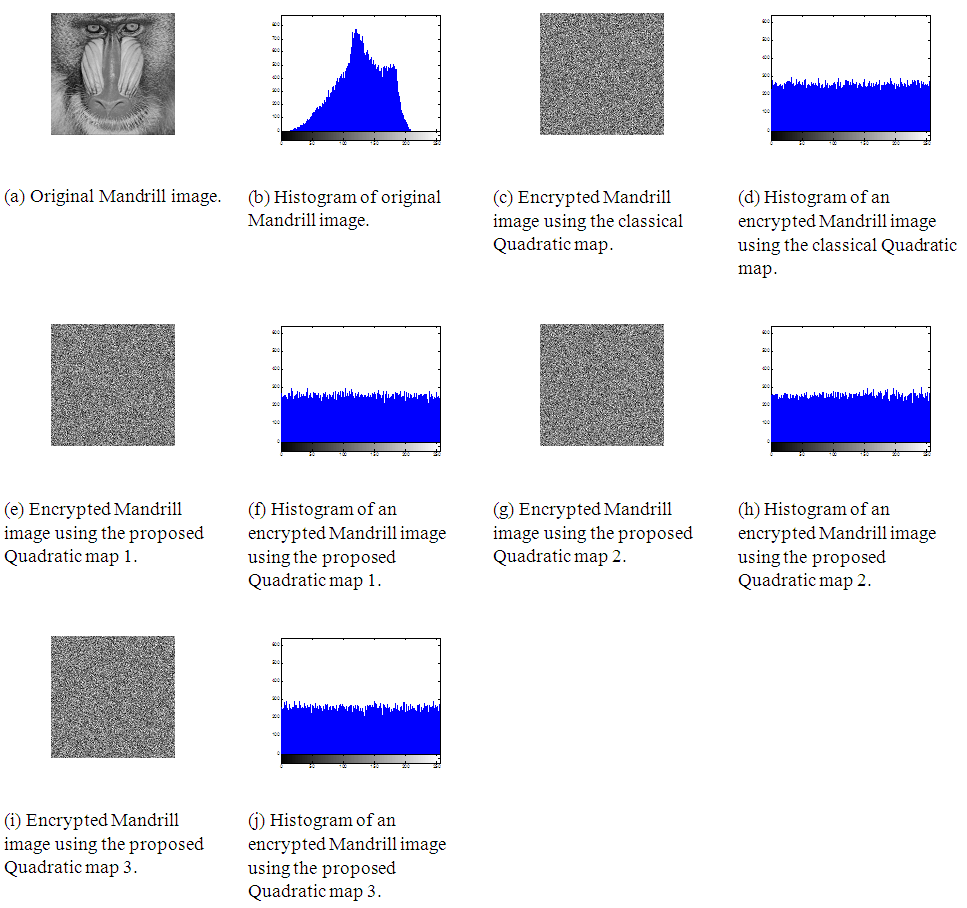 | Figure 13. Mandrill image encryption with the classical and proposed Quadratic maps |
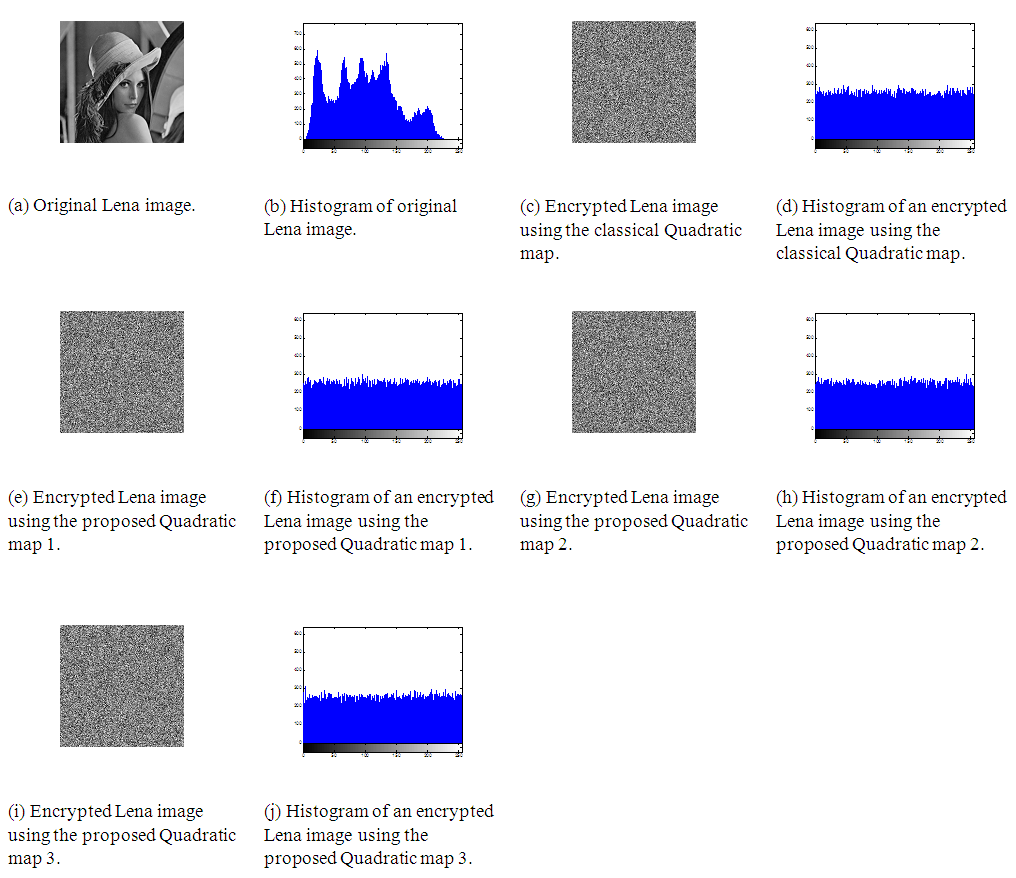 | Figure 14. Lena image encryption with the classical and proposed Quadratic maps |
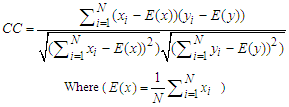 | (14) |
|
6.1.3. Sensitivity Analysis
- In general, an encrypted image must be sensitive to the small changes in the original image and secret key. In order to avoid differential attack, a small change in the plain image or secret key should cause a significant change in the encrypted image. Two parameters were used for differential analysis; Net Pixel Change Rate (NPCR) and Unified Average Changing Intensity (UACI) [28]. NPCR measures the number of pixels change rate of encrypted image while one pixel of the original image is changed. UACI measures the average intensity of the differences between those two images. The NPCR and UACI of two encrypted images are defined in Eqs. (15), (16) respectively. C1 and C2 are two encrypted images, whose corresponding plain images have only one pixel change.
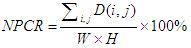 | (15) |
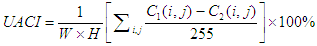 | (16) |
|
6.2. Processing Time
- The processing time is the time required to encrypt and decrypt an image. The smaller the processing time, the better is the encryption efficiency. The proposed scheme uses only one round for diffusion process, and so this reduces the encryption/decryption time, and hence the scheme is practicable in real time applications. All the calculations are performed using MATLAB R2007a software under windows XP operating system, processor core 2 duo, 1.6 GHz and 2G RAM. For the 256 gray level Cameraman, Mandrill, and Lena images, the processing time is listed in Table (3). It is clear that the processing time of the proposed scheme is within 75 seconds, which is smaller than the processing time of RC6, and DES. Chaotic Baker map has the smallest processing time, because it is just a permutation map.
7. Conclusions
- In this paper, new Quadratic chaotic maps with better chaotic properties have been proposed. These maps increase the available chaotic range of parameter r to infinity, and hence are more robust against attacks compared to the limited value of parameter r in the classical Quadratic map. The MLE in the proposed Quadratic maps is increased compared to the classical Quadratic map up to 3.4709, while it was 0.6720 in the classical Quadratic map. Therefore, the proposed Quadratic maps are more effective than the classical Quadratic map in the encryption process and more sensitive to the initial conditions. An encryption scheme of permutation and diffusion combining two chaotic maps has been presented and investigated. In the permutation process, we sort chaotic sequences of the Chepyshev map to shuffle the image. This procedure avoids the cycle of chaotic numbers in the generation of the permutation key. In the diffusion process, the permuted image is then encrypted by the key related to the plain image algorithm using the proposed Quadratic maps. In this encryption scheme, the key depends on both the initial key and the original image. So it can survive known plain text attack. This algorithm uses a single round of diffusion, and hence it has low computational complexity. The proposed encryption scheme effectively resists the brute-force attack due to its very large key space. Furthermore, security, statistical, and sensitivity analysis has been carried out demonstrating high security and robustness of the proposed scheme. This proposed scheme is suitable for real-time image encryption applications due to its small processing time compared to the other encryption schemes. A comparative study have been presented between the proposed scheme, RC6, DES and chaotic Baker map. The results of this comparison show that the proposed scheme using the proposed Quadratic maps has a superior performance.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML