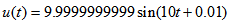-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2015; 5(1): 13-21
doi:10.5923/j.ajsp.20150501.03
A Novel Cryptographic System with Adjustable Secret Key Space for Color Image Security Using Nonlinear Adaptive Filter
Hung-I Hsiao, Junghsi Lee
Department of Electrical Engineering, Yuan Ze University, Taiwan
Correspondence to: Hung-I Hsiao, Department of Electrical Engineering, Yuan Ze University, Taiwan.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In this paper, we propose a novel chaos-based cryptographic system for enhancing color image security by using chaotic amplitude phase frequency model nonlinear adaptive filter. The advantage of the proposed scheme is that it possesses the ability of “adjustable secret key space” in order to get the enough security strength to protect color image. Furthermore, the experimental results and security analyses demonstrate that the proposed method has a fine security performance. The “adjustable secret key space” can overcome the security strength issue for obtaining enough secret key length, which can use external signal to adjust the required secret key space without changing the original cryptographic infrastructure.
Keywords: Color image encryption, Adjustable secret key space, Chaos
Cite this paper: Hung-I Hsiao, Junghsi Lee, A Novel Cryptographic System with Adjustable Secret Key Space for Color Image Security Using Nonlinear Adaptive Filter, American Journal of Signal Processing, Vol. 5 No. 1, 2015, pp. 13-21. doi: 10.5923/j.ajsp.20150501.03.
Article Outline
1. Introduction
- The discussions of the image security depict its importance shown in [1, 2]. To achieve the purpose of safe transmission and access of image, we propose a new cryptographic system which possesses the ability of adjustable secret key space, and the proposed scheme is designed by chaotic amplitude phase frequency model (APFM) nonlinear adaptive filter [3]. Among the modern encryption methods, Data Encryption Standard (DES) [4] and Advanced Encryption Standard (AES) [5] are the most typical. Besides, many chaotic encryption methods [6-8] have been researched in recent years. The chaos-based encryption schemes are the most noticeable due to the chaos excellent characteristics such as the sensitivity to initial conditions, and semi-randomness behaviors; the chaos excellent properties make the chaos-based cryptography possess nice randomness in encrypted image [9]. However, in the above-mentioned encryption methods, they can not use external signal to adjust the required secret key space in order to obtain sufficient security strength. For example, DES is a symmetric-key block cipher published by the National Institute of Standards and Technology (NIST) in 1977. DES’s most serious weakness is the small secret key length, only 56 bits, causing all secret key space of DES to be
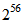 [10]. This weakness could make the ciphers fragile to be brute-force attacked, so DES is later replaced by AES. AES, the current encryption standard which is a symmetric-key block cipher published by NIST in 2001, has three different secret key lengths: 128, 192, and 256 bits, i.e., the corresponding secret key spaces are
[10]. This weakness could make the ciphers fragile to be brute-force attacked, so DES is later replaced by AES. AES, the current encryption standard which is a symmetric-key block cipher published by NIST in 2001, has three different secret key lengths: 128, 192, and 256 bits, i.e., the corresponding secret key spaces are 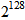 ,
, 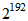 , and
, and 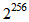 , respectively [11]. Clearly, the secret key length and its corresponding secret key space decide the security strength of the cryptographic system. Table 1 shows the recommendations of security-strength time frames published by NIST Special Publication 800-57 in 2012 [12], which is a schedule of the security strength for different secret key lengths that provide five types of lengths including 80, 112, 128, 192, and 256 bits. As shown in Table 1, because the two types of security strength, 80 and 112 bits, are not strong enough to protect data, both of the secret key lengths are placed in the “Disallowed” after 2013 and 2030, respectively. On the contrary, the secret key lengths 128, 192, and 256 bits are “Acceptable” from 2011-2031 and beyond, and the minimum of the secret key length for “Acceptable” is 112 bits of security strength, which is acceptable until 2030. We can find that the change of time frame is an important factor for obtaining the enough security strength of secret key length. Based on the above discussions, we propose a new cryptographic system possessing adjustable secret key space, which also means that the secret key length is adjustable, and it is designed by chaotic APFM nonlinear adaptive filter whose input signal can control the size of secret key space. That is, the proposed scheme can use external signal to adjust the required secret key space without altering the original cryptographic infrastructure, so the security strength is sufficient to protect color images even it is way beyond the indicated time frames given in Table 1.
, respectively [11]. Clearly, the secret key length and its corresponding secret key space decide the security strength of the cryptographic system. Table 1 shows the recommendations of security-strength time frames published by NIST Special Publication 800-57 in 2012 [12], which is a schedule of the security strength for different secret key lengths that provide five types of lengths including 80, 112, 128, 192, and 256 bits. As shown in Table 1, because the two types of security strength, 80 and 112 bits, are not strong enough to protect data, both of the secret key lengths are placed in the “Disallowed” after 2013 and 2030, respectively. On the contrary, the secret key lengths 128, 192, and 256 bits are “Acceptable” from 2011-2031 and beyond, and the minimum of the secret key length for “Acceptable” is 112 bits of security strength, which is acceptable until 2030. We can find that the change of time frame is an important factor for obtaining the enough security strength of secret key length. Based on the above discussions, we propose a new cryptographic system possessing adjustable secret key space, which also means that the secret key length is adjustable, and it is designed by chaotic APFM nonlinear adaptive filter whose input signal can control the size of secret key space. That is, the proposed scheme can use external signal to adjust the required secret key space without altering the original cryptographic infrastructure, so the security strength is sufficient to protect color images even it is way beyond the indicated time frames given in Table 1.
|
2. Chaotic APFM Nonlinear Adaptive Filter
- The equation of APFM nonlinear adaptive filter is as follows: [13]
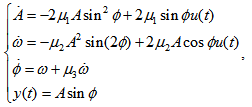 | (1) |
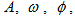 and
and 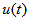 refer to amplitude, frequency, phase angle of the desired component, and input signal, respectively. The parameters
refer to amplitude, frequency, phase angle of the desired component, and input signal, respectively. The parameters 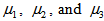 are the filter step sizes for controlling the speed of the filter,
are the filter step sizes for controlling the speed of the filter, 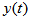 is the filter output, and
is the filter output, and 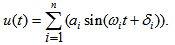 | (2) |
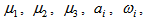
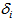 , for
, for 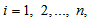 simulated time interval, and initial values for the APFM nonlinear adaptive filter to generate chaotic trajectories. The APFM nonlinear adaptive filter could produce chaos in accordance with the numerical simulation results by Matlab tools using the ordinary differential equation (ODE) solver and solving on a simulated time interval
simulated time interval, and initial values for the APFM nonlinear adaptive filter to generate chaotic trajectories. The APFM nonlinear adaptive filter could produce chaos in accordance with the numerical simulation results by Matlab tools using the ordinary differential equation (ODE) solver and solving on a simulated time interval 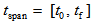 , when
, when 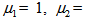
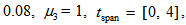 with an arbitrarily small initial values
with an arbitrarily small initial values 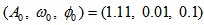 , computed precision is
, computed precision is 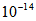 , and
, and 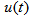 chooses the following three cases:
chooses the following three cases:  As depicted in Figs. 1-3, which respectively refer to above Cases 1-3,
As depicted in Figs. 1-3, which respectively refer to above Cases 1-3,  is a controlled parameter, also known as bifurcation parameter, for the APFM nonlinear adaptive filter. The chaotic diagrams of this APFM nonlinear adaptive filter are shown in Figs. 1-3, whose sub-Figs. (a)-(c) denote the
is a controlled parameter, also known as bifurcation parameter, for the APFM nonlinear adaptive filter. The chaotic diagrams of this APFM nonlinear adaptive filter are shown in Figs. 1-3, whose sub-Figs. (a)-(c) denote the  plane,
plane, 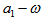 plane, and
plane, and 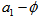 plane, respectively.
plane, respectively.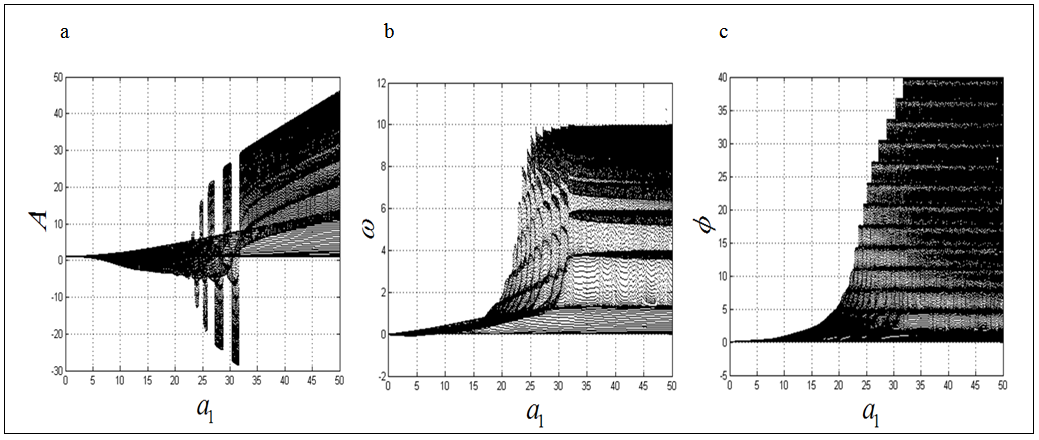 | Figure 1. APFM nonlinear adaptive filter chaotic trajectories for Case 1, the parameters are  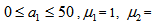 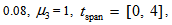 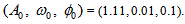 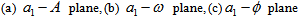 |
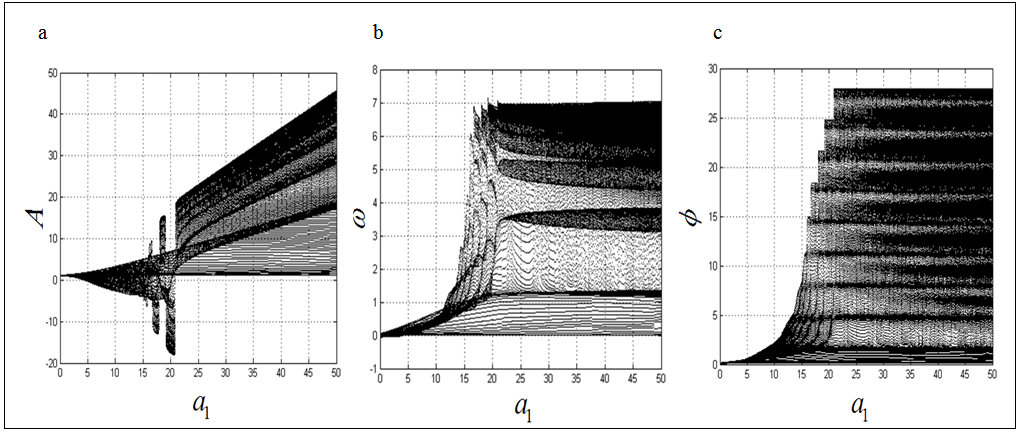 | Figure 2. APFM nonlinear adaptive filter chaotic trajectories for Case 2, the parameters are 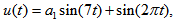 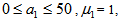 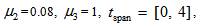   |
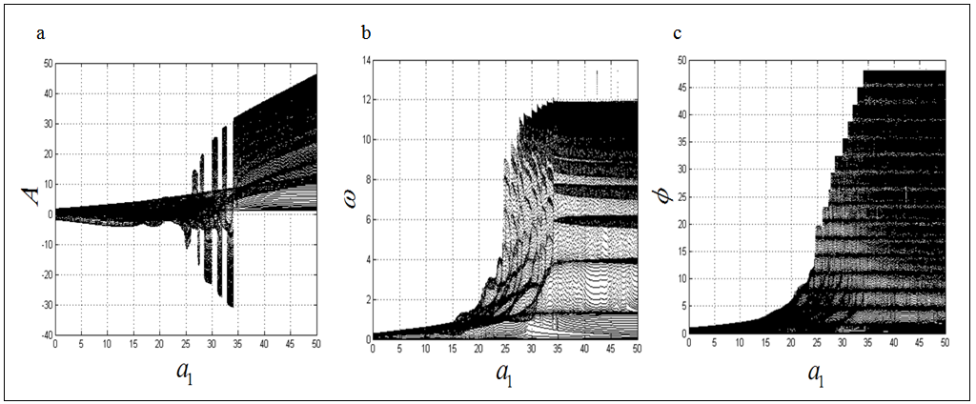 | Figure 3. APFM nonlinear adaptive filter chaotic trajectories for Case 3, the parameters are  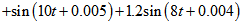 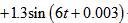 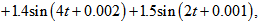 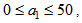 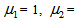 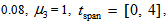 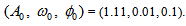 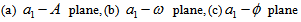 |
3. The Proposed Color Image Encryption/Decryption Algorithm
- The design of color image encryption algorithm is shown as follows:Step 1: Supposing the size of original color image is
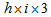 , h and i denote the width and height, respectively. We randomly choose three pixels named
, h and i denote the width and height, respectively. We randomly choose three pixels named 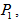
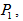 and
and 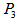 in the original image. Compute the value
in the original image. Compute the value 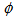 by
by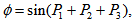 | (3) |
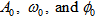 by
by 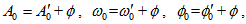 | (4) |
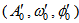 are the given initial values.Step 2: Giving the encrypted parameters for APFM nonlinear adaptive filter :
are the given initial values.Step 2: Giving the encrypted parameters for APFM nonlinear adaptive filter : 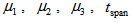 , initial values
, initial values 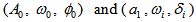 .Step 3: acquiring the APFM nonlinear adaptive filter 3 solutions
.Step 3: acquiring the APFM nonlinear adaptive filter 3 solutions 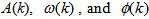 , then preprocess by Eqs. (5)~(7), for
, then preprocess by Eqs. (5)~(7), for 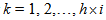 .
.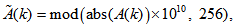 | (5) |
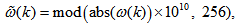 | (6) |
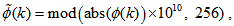 | (7) |
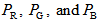 . Step 5: Generating three
. Step 5: Generating three 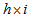 cipher keys
cipher keys 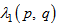 ,
,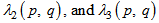 obtained by
obtained by 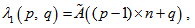 | (8) |
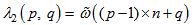 | (9) |
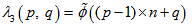 | (10) |
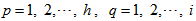 .Step 6: Executing the exclusive-or operation between gray images and cipher keys, and then get three
.Step 6: Executing the exclusive-or operation between gray images and cipher keys, and then get three 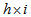 gray cipher images
gray cipher images 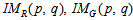
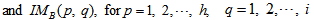 , which are computed by as follows:
, which are computed by as follows: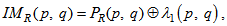 | (11) |
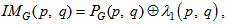 | (12) |
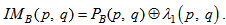 | (13) |
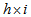 gray cipher images
gray cipher images 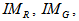 and
and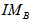 into
into 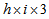 color cipher image.The decryption algorithm is opposite to the encryption scheme due to the decrypted operation is reversed to the process for encryption, and the decrypted parameters are all the same encrypted parameters [14].
color cipher image.The decryption algorithm is opposite to the encryption scheme due to the decrypted operation is reversed to the process for encryption, and the decrypted parameters are all the same encrypted parameters [14]. 4. Experimental Results
4.1. Encryption
- We use the color Lena image (Fig. 4(a)) with size
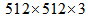 is served as the color original image whose red, green, and blue components are separately shown in Figs. 4(b)-4(d), and the corresponding histograms are shown in Figs. 4(e)-4(g), respectively. The encrypted parameters of APFM nonlinear adaptive filter are
is served as the color original image whose red, green, and blue components are separately shown in Figs. 4(b)-4(d), and the corresponding histograms are shown in Figs. 4(e)-4(g), respectively. The encrypted parameters of APFM nonlinear adaptive filter are 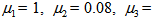
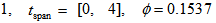 , given initial values
, given initial values 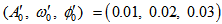 computed precision is
computed precision is 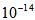 , choosing three different u(t), which are the same as the three cases of u(t) shown in Section 2 except the parameter
, choosing three different u(t), which are the same as the three cases of u(t) shown in Section 2 except the parameter 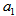 that ranges in
that ranges in 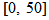 , and the three cases are as follows:
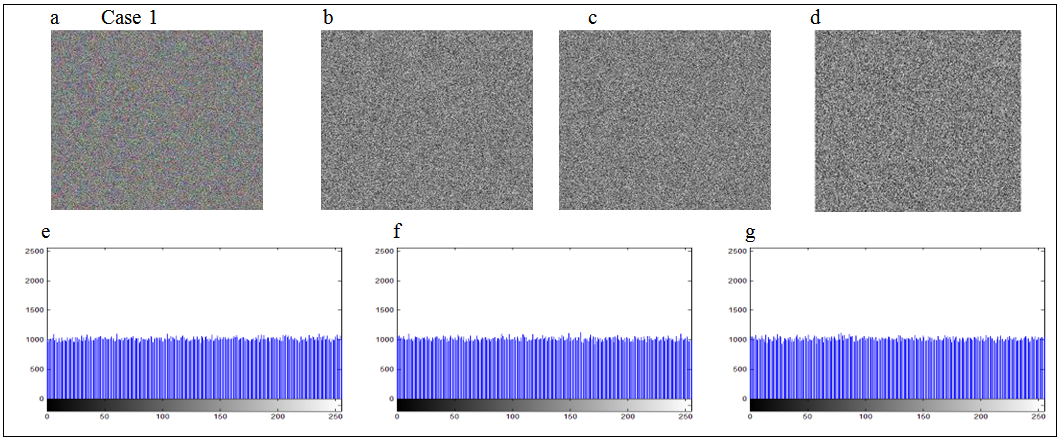
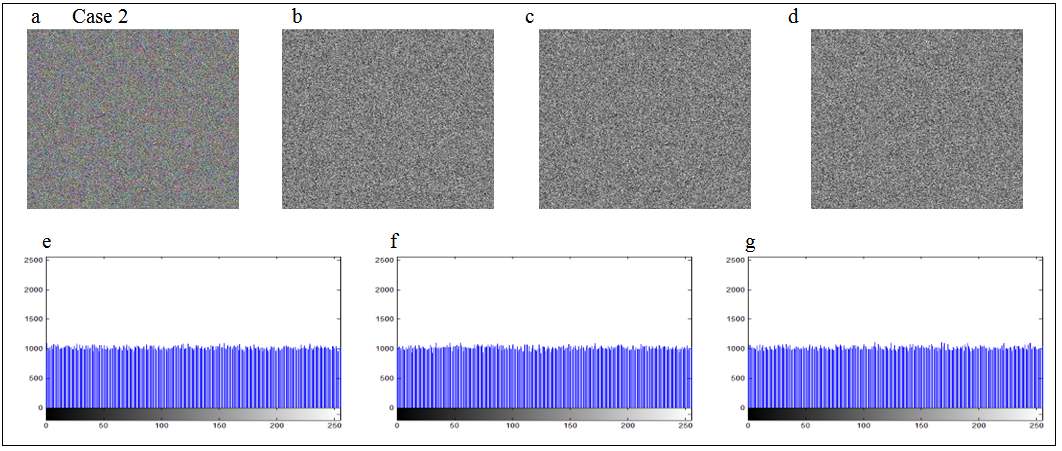
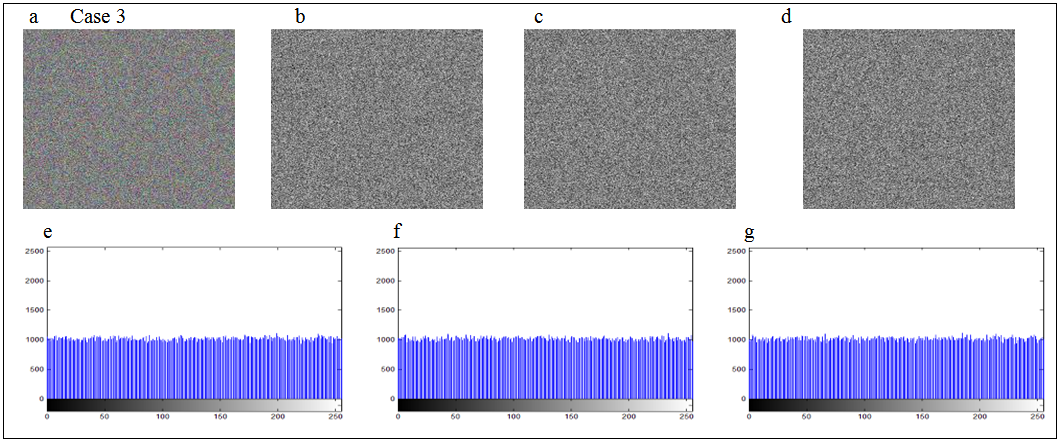
, and the three cases are as follows: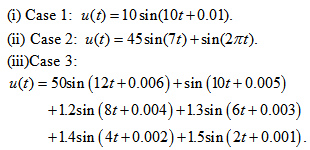 The encrypted images and corresponding histograms are depicted in Figs. 5-7, which separately refer to Cases 1-3, in which the sub-fig. (a) denotes the color cipher image, sub-figs. (b)-(d) show the red, green, and blue components of color cipher image, respectively, and sub-figs. (e)-(g) depict the histograms of red , green, and blue components of color cipher image, separately.
The encrypted images and corresponding histograms are depicted in Figs. 5-7, which separately refer to Cases 1-3, in which the sub-fig. (a) denotes the color cipher image, sub-figs. (b)-(d) show the red, green, and blue components of color cipher image, respectively, and sub-figs. (e)-(g) depict the histograms of red , green, and blue components of color cipher image, separately. 4.2. Decryption
- For explaining the decryption, we use the color cipher image shown in Fig. 5(a) (i.e., generated by Case 1, the encrypted parameters are
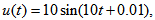 etc.) for explaining the decryption. (1) uccessful decryptionThe decrypted parameters are all the same as the encrypted parameters of Case 1, which are given in Section 4.1. As depicted in Fig. 8(a), the decrypted image is successful to recover the color Lena image from color cipher image (Fig. 5(a)) due to the correct decrypted parameters.(2) ailed decryptionThe decrypted parameters are also same as the encrypted parameters of Case 1, which are shown in Section 4.1, except the input signal
etc.) for explaining the decryption. (1) uccessful decryptionThe decrypted parameters are all the same as the encrypted parameters of Case 1, which are given in Section 4.1. As depicted in Fig. 8(a), the decrypted image is successful to recover the color Lena image from color cipher image (Fig. 5(a)) due to the correct decrypted parameters.(2) ailed decryptionThe decrypted parameters are also same as the encrypted parameters of Case 1, which are shown in Section 4.1, except the input signal 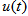 that are chosen as
that are chosen as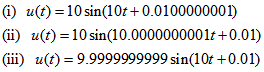 As shown in Figs. 8(b)-8(d), which refer to above 3 different u(t), the decrypted images for color cipher image (Fig. 5(a)) are not successful due to the incorrect input signal
As shown in Figs. 8(b)-8(d), which refer to above 3 different u(t), the decrypted images for color cipher image (Fig. 5(a)) are not successful due to the incorrect input signal  of APFM nonlinear adaptive filter.
of APFM nonlinear adaptive filter.5. Security Analyses
5.1. Adjustable Secret Key Space Controlled by Input Signal of APFM Nonlinear Adaptive Filter
- The chaotic behavior of APFM nonlinear adaptive filter can design our proposed cryptographic system, we use this nonlinear filter to design encryption/decryption algorithm. The parameters, input signal, simulated time interval , and initial values of the APFM nonlinear adaptive filter can be used as the secret keys for proposed cryptographic system, so there are these secret keys
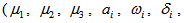
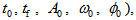 for
for 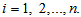 The total secret key space
The total secret key space 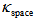 is
is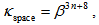 | (14) |
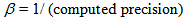 . The value n depends on the input signal u(t) of APFM nonlinear adaptive filter. We can choose three different u(t) to control the size of secret key space, i.e., the proposed scheme possesses the characteristic of adjustable secret key space. This means that the proposed scheme can use outer signal to adjust the desired secret key space without changing original cryptographic architecture. The size of secret key space
. The value n depends on the input signal u(t) of APFM nonlinear adaptive filter. We can choose three different u(t) to control the size of secret key space, i.e., the proposed scheme possesses the characteristic of adjustable secret key space. This means that the proposed scheme can use outer signal to adjust the desired secret key space without changing original cryptographic architecture. The size of secret key space 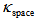 depends on input signal u(t) of the APFM nonlinear adaptive filter. If the computed precision is
depends on input signal u(t) of the APFM nonlinear adaptive filter. If the computed precision is 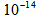 , calculate the secret key space for three different cases of u(t) by Eq. (14), which are
, calculate the secret key space for three different cases of u(t) by Eq. (14), which are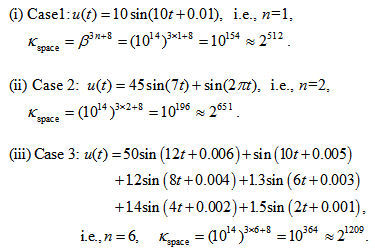 The above three secret key spaces
The above three secret key spaces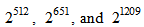 (i.e., the corresponding secret key lengths are 512, 651, 1209 bits, respectively.) are enough to prevent all kinds of brute-force attacks [15]. Furthermore, the three different input signal u(t) of APFM nonlinear adaptive filter can control the size of secret key space in order to acquire required security strength. Table 2 shows the comparison of secret key space with the proposed method and other scheme, in which the secret key space of proposed method is superior to the other schemes.
(i.e., the corresponding secret key lengths are 512, 651, 1209 bits, respectively.) are enough to prevent all kinds of brute-force attacks [15]. Furthermore, the three different input signal u(t) of APFM nonlinear adaptive filter can control the size of secret key space in order to acquire required security strength. Table 2 shows the comparison of secret key space with the proposed method and other scheme, in which the secret key space of proposed method is superior to the other schemes.
|
5.2. Histogram
- The histograms of red, green and blue components for three cases of color cipher images, which are respectively shown in sub-Figs. (e)-(g) of Figs. 5-7, are almost uniformly distributed. The nearly uniform distribution of histograms can resist the statistical analysis attacks [16].
5.3. Correlation Analysis
- The criterion for correlation analysis is computed by the correlation coefficient which is calculated by the following formulas [17]
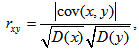 | (15) |
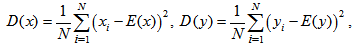 | (16) |
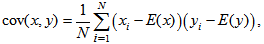 | (17) |
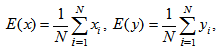 | (18) |
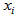 and
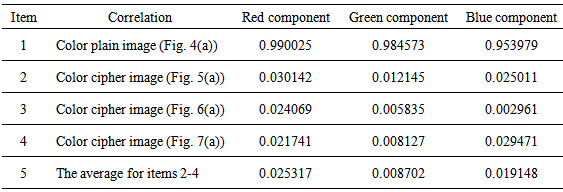
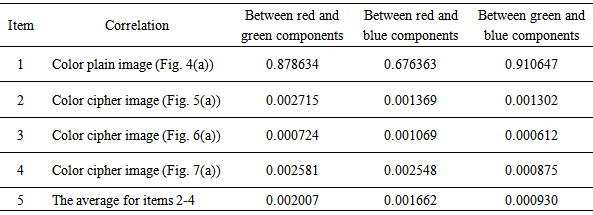
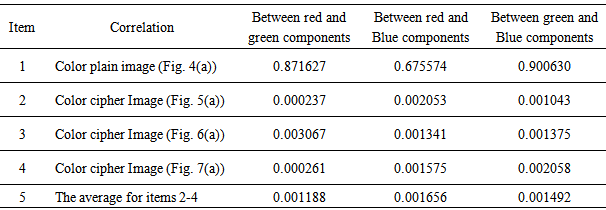
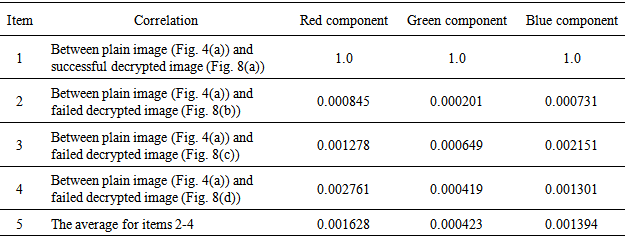
and 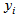 respectively denote gray level values of two different pixels in the image itself or between two different images, cov(x, y) indicates the covariance, D(x), D(y) represents the variance, and E(x), E(y) denotes the mean.Table 3 gives the correlation coefficients of two adjacent pixels, in which we use the sample data that are randomly selected for 3000 pairs of two adjacent pixels from red, green, and blue components of color plain image and three color cipher images in the direction mixing horizontal, vertical, and diagonal direction simultaneously. Table 3 depicts the 3 correlation coefficient average values for three cipher images (i.e., item 5) are very small (they are close to ideal value 0.0) compared with those of color plain image (i.e., item 1 whose 3 correlation coefficient values are close to 1.0). Similar to Table 3, Tables 4 and 5 respectively show the correlation coefficients of the same position and adjacent position among red, green, and blue components of color plain image and color cipher images, in which the 3 correlation coefficient average values (i.e., item 5 for Tables 4 and 5) for three cipher images are much smaller (they also approach to ideal value 0.0) than those of color plain image (i.e., item 1 for Tables 4 and 5). Tables 3-5 display the nice encryption property on proposed method, in which it gives the near zero correlation between color plain image and color cipher image. Tables 4-5 depict the proposed method can effectively reduce the correlations among red, green, blue components of color cipher image. Table 6 shows the correlation coefficients of all pixels of three components between color plain image and decrypted images, in which the three correlation coefficient values of three components between plain image and successful decrypted image are 1.0 (i.e., item 1) denoting the successful decrypted image (Fig. 8(a)) is all the same as the original color image (Fig. 4(a)). The result represents that the successful decrypted image possesses the property of no distortion. Conversely, in the item 5 of Table 6, the three correlation coefficient average values of three components between plain image and failed decrypted images are much smaller (they are near to ideal value 0.0), which denotes the failed decrypted image and original color image are almost uncorrelated, and it also shows the nice cryptographic characteristic in ciphers.
respectively denote gray level values of two different pixels in the image itself or between two different images, cov(x, y) indicates the covariance, D(x), D(y) represents the variance, and E(x), E(y) denotes the mean.Table 3 gives the correlation coefficients of two adjacent pixels, in which we use the sample data that are randomly selected for 3000 pairs of two adjacent pixels from red, green, and blue components of color plain image and three color cipher images in the direction mixing horizontal, vertical, and diagonal direction simultaneously. Table 3 depicts the 3 correlation coefficient average values for three cipher images (i.e., item 5) are very small (they are close to ideal value 0.0) compared with those of color plain image (i.e., item 1 whose 3 correlation coefficient values are close to 1.0). Similar to Table 3, Tables 4 and 5 respectively show the correlation coefficients of the same position and adjacent position among red, green, and blue components of color plain image and color cipher images, in which the 3 correlation coefficient average values (i.e., item 5 for Tables 4 and 5) for three cipher images are much smaller (they also approach to ideal value 0.0) than those of color plain image (i.e., item 1 for Tables 4 and 5). Tables 3-5 display the nice encryption property on proposed method, in which it gives the near zero correlation between color plain image and color cipher image. Tables 4-5 depict the proposed method can effectively reduce the correlations among red, green, blue components of color cipher image. Table 6 shows the correlation coefficients of all pixels of three components between color plain image and decrypted images, in which the three correlation coefficient values of three components between plain image and successful decrypted image are 1.0 (i.e., item 1) denoting the successful decrypted image (Fig. 8(a)) is all the same as the original color image (Fig. 4(a)). The result represents that the successful decrypted image possesses the property of no distortion. Conversely, in the item 5 of Table 6, the three correlation coefficient average values of three components between plain image and failed decrypted images are much smaller (they are near to ideal value 0.0), which denotes the failed decrypted image and original color image are almost uncorrelated, and it also shows the nice cryptographic characteristic in ciphers.
|
|
|
|
6. Conclusions
- In this paper, a novel cryptographic system with adjustable secret key space for color image security using the chaotic APFM nonlinear adaptive filter is proposed, in which the adjustable secret key space overcomes the issue for acquiring enough security strength of secret key length. The color cipher images possess nice randomness properties for color image security. The security analyses demonstrate that the proposed scheme is a secure cryptographic system.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML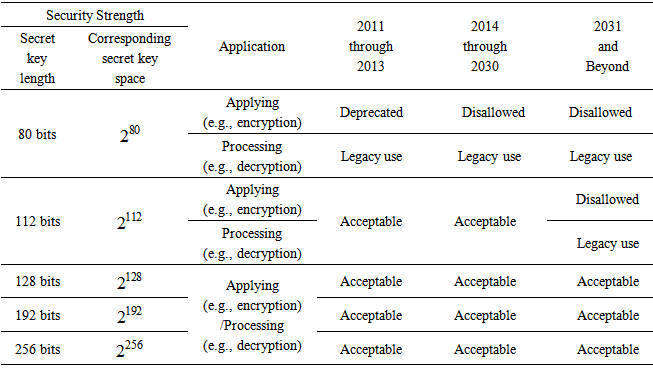

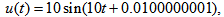 (c) failed decryption due to incorrect
(c) failed decryption due to incorrect 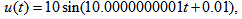 (d) failed decryption due to incorrect
(d) failed decryption due to incorrect