1. Introduction

Teaching is the process of educating or instructing who are ignorant of particular phenomena. Teaching has always been considered as service, so like any other service, when one is not competent is probably unethical[1]. There are three main types of learning styles: auditory, visual, and kinaesthetic[2]. Practically, a class of students is a group of people having a combination of these three learning styles. In this information technology age, the students are no more auditory, but with a learning style of visual and kinaesthetic styles. So, when a teacher teaches especially science or engineering, mere lectures alone could not help the students to understand and appreciate the concepts. This stands as a challenge for higher education teachers and motivates them to adapt visual and experimentation based teaching[3].

Digital image processing is the process of processing digital images with various techniques such as restoration, denoising, segmentation, edge detection etc... Now a days, digital image processing plays a vital role in day-to-day life including (not limited to) multimedia communication, medical diagnostics, astronomy, weather forecasting, pattern matching and recognition (Vehicle number plate recognition, finger print and palm print recognition) for security applications, forensics, geographical information systems, human computer interfaces, industrial inspection, document processing, remote sensing and satellite image processing[4]. Teaching digital image processing is a challenge for the young teachers who are handling students of all learning styles. It is worth mentioning the avowal of Confucius, the great Chinese philosopher that “I hear and I forget. I see and I remember. I do and I understand”. Hence, Visual and experimental learning methods can influence the students much better than mere lecturing[3]. Digital image processing concepts can easily be understood if they are taught using visual, experimental and interactive methods.

MATLAB (MATrix LABoratory) is a computing platform that is suitable for developing and testing various engineering, science and management applications. It is a high level programming environment that is equipped with a good number of toolboxes with functions for integrating MATLAB based algorithms with external applications and languages such as C, C++, Java, .NET and Microsoft excel. The MATLAB language provides native support for the vector and matrix operations that are fundamental to solving engineering and scientific problems, enabling fast development and execution. With the MATLAB language, the programs and algorithms can be developed faster than with traditional languages. In many cases, the support for vector and matrix operations eliminates the need for lengthy for-loops. So, a single line of MATLAB code can often replace several lines of C or C++ code. MATLAB also provides features of traditional programming languages, such as flow control, error handling, and object-oriented programming (OOP). Apart from the fundamental data types, MATLAB allows user defined data type too. Immediate results can be produced by interactively executing commands one at a time. This approach helps to quickly explore multiple options and iterate to an optimal solution[4]. GUIDE (Graphical User Interface Development Environment), is the tool in MATLAB to lay out, design, and edit custom graphical user interfaces by including common controls such as list boxes, pull-down menus, and push buttons, as well as MATLAB plots. Graphical user interfaces can also be created programmatically using MATLAB functions[5]. This interactive GUI helps the teacher to make the student understand in a better way the concepts behind the image processing techniques.

The rest of this article is organized as follows. Section 2 reviews the image processing concepts namely image denoising, image segmentation and edge detection. Section 3 presents the practical oriented teaching and learning method for understanding the image processing concepts with MATLAB. Finally, the paper is concluded in section 4.

2. Review of Digital Image Processing Concepts

An image is defined as the 2-D representation of the 3D scene. A digital image is regarded as the numeric representation of the 2D image in a sampled and quantized form. The basic picture element is called pixel and an MXN image has M rows of pixels and N columns of pixels. It can also be thought of a 2D grid or matrix whose elements are represented by f(x,y), where x and y are the coordinates of the grid or the indices of the matrix elements. Digital image processing deals with processing of digital images with the help of computer algorithms. There are a number of image processing methods based on the applications. In this paper, the issues in teaching image denoising, segmentation and edge detection are addressed.

2.1. Image Denoising

Digital images are corrupted by various types of noises during acquisition and transmission. These noisy components must be eliminated before it can be used for further process or analysis. The different types of noises that are most commonly encountered are gaussian noise[6] and salt and pepper noise[7]. Gaussian noise can easily be eliminated by simple average filter/mean filter[4]. This noise removal process is basically the convolution operation between the selected window of the image and the filter kernel slide over the entire image. If f(i,j) is the processing pixel, then the selected window of size 3X3 with the center pixel as processing pixel can be defined as W = {f(i-1,j-1), f(i-1,j),f(i-1,j+1);f(i,j-1),f(i,j),f(i,j+1);f(i+1,j-1),f(i+1,j),f(i+1,j+1)}. The filter kernel of a mean/average filter is defined as K = {k₁, k₂, k₃; k₄, k₅, k₆, k₇, k₈, k₉}. The formation of window and a typical 3X3 mean/average filter are shown in Figure 1. When the kernel ‘K’ is applied on the entire image in a pixel by pixel manner, each pixel is replaced by the average value of the 3X3 neighbourhood, hence the resulting image will be free from gaussian noise components[8]. The major drawback of average filter is that it may oversmooth the edges so that the image is blurred.

Figure 1. (a) 2D grid representation of a digital image showing a sample window in gray shade, (b) Typical 3X3 average filter kernel

Salt and pepper noise is an impulsive type of noise that represents the presence of randomly occurring black and white pixels. In an 8-bit image, if the gray level values ‘0’ or ‘255’ exist then the corresponding pixel is considered to be a noisy pixel. The removal of impulse noise involves median filter which is conceptually similar to that of the mean/average filter. The processing pixel is replaced by median of the 3X3 neighbourhood. If the selected 3X3 window is W = {12, 123, 0, 56, 0, 78, 45, 55, 55} with the processing pixel as ‘0’, then the window elements are arranged in ascending order (W = {0, 0, 12, 45, 55, 55, 56, 78, 123}), and the mid value is taken as median (i.e 55), and the processing pixel ‘0’ will be replaced by the median value ‘55’. The major advantage of median filter is that it can preserve details of the image such as edges and contours[4, 7].

2.2. Image Segmentation

Image segmentation is a process of identifying homogeneous regions in a digital image. The basic idea behind segmentation is called thresholding which can be classified as single thresholding and multiple thresholding[9]. Selecting an optimal threshold is a crucial process in segmentation. In single thresholding, a simple thresholding strategy is followed as given in equation (1).

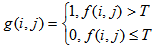(1)

‘T’ is a predefined threshold, and the pixels replaced by ‘1’ belong to the object and the pixels replaced by ‘0’ belong to the background of the image. If it is required to identify more than two homogeneous regions in the image, the multiple thresholding technique may be adopted. For example, two threshold values T₁, T₂ with T₁<T₂, can segment the entire image into three homogeneous regions and for each region, distinct gray level (G₁, G₂ and G₃) may be assigned. The multiple thresholding technique is mathematically represented as equation (2).

(2)

Segmentation could be used for object recognition, occlusion boundary estimation within motion or stereo systems, image compression, image editing, or image database look-up, Content-based image retrieval, Medical imaging, Locating tumours and other pathologies, Face detection, Fingerprint recognition, Iris recognition, Traffic control systems and Video surveillance. Apart from threshold based segmentation, there are other various segmentation techniques including cluster based methods, compression based method, histogram based methods, Region-growing methods, Split-and-merge methods, Partial differential equation-based methods, level set method and watershed transformation[4, 9].

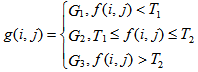2.3. Edge Detection

Edge detection is the common approach for detecting meaningful discontinuities in gray levels such as edges[10, 11]. The basic idea behind this edge detection is that, edges can be understood as discontinuities that can be detected by applying the first or second order partial derivatives. The gradient (Sobel row-edge detector and & Prewitt column- edge detector) or Laplacian of Gaussian edge detector can be applied on the image to detect edges. The sample kernel for Sobel edge detector, Prewitt edge detector and Laplacian of Gaussian are shown in Figure 2 and 3X3 Laplacian mask and 5X5 Laplacian of Gaussian mask are shown in Figure 3. The Prewitt and Sobel operators are widely used in digital gradient computation. Among these two the Sobel operator is preferred because of its higher noise suppression characteristics[4]. The Laplacian mask shown in Figure 3 can also be used for detecting point discontinuities. From Figure 2 and Figure 3 it is evident that all the edge detection masks are having elements that sums to zero, resulting in a response of ‘0’ at smooth regions of the image.

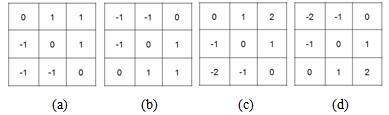Figure 2. (a,b) Prewitt mask, (c,d) Sobel mask for diagonal edge detection

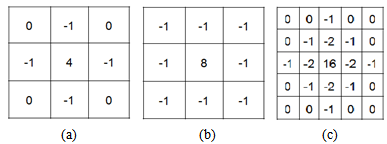Figure 3. (a,b) Laplacian mask, (c) Typical 5X5 Laplacian of gaussian mask

3. Teaching Image Processing Concepts with Matlab – A Practical Approach

MATLAB consist of an excellent GUIDE and set of functions for different applications in various disciplines. This platform has four major components namely command window, workspace, editor and product help as shown in Figure 4. For application development either the .m file editor or GUI can be used. MATLAB has been successfully used as an effective tool to teach robotics[12], electrical engineering[13-17], communication[18] and data analysis[19]. As evident from[3], visual based teaching methodologies can improve the understanding and performance of the students. This section addresses the practical use of MATLAB in teaching image processing concepts. The discussion is restricted to the simple and widely used image processing concepts namely image denoising, segmentation and edge detection. Some features of MATLAB image processing toolbox are listed in Table 1.

Figure 4. Typical MATLAB window

Table 1. Some features of MATLAB image processing toolbox Feature Support Image Source Digital cameras, satellite and airborne sensors, medical imaging devices, microscopes, telescopes, and other scientific instruments. Data types Single-precision and double-precision floating-point and signed and unsigned 8-bit, 16-bit, and 32-bit integers. Image format PEG, JPEG-2000, TIFF, PNG, HDF, HDF-EOS, FITS, Microsoft® Excel®, ASCII, and binary files. Simple operations Resizing, rotating, and cropping, more complex 2D geometric transformations such as affine and projective. External applications and Languages C, C++, Java, .NET and Microsoft excel

3.1. Teaching the Concepts of Image Denoising with MATLAB

The image processing toolbox has dedicated functions to read, write, and display images. Also for implementing image filtering the function imfilter(I,h) can be used where I and h are the multidimensional array that represents the image and filter respectively[20]. A sample code for teaching gaussian noise removal using a simple average filter and the output images are shown ion Figure 5. On seeing figure 5, it is clear that when 3X3 average filter is used the gaussian noise components in the background are not removed completely where as when 5X5 average filter is used the output image looks much blurred compared that of the 3X3 average filter. This simple exercise will be very helpful to teach the effect of the filter kernel size on the filtered image[4,8,21].

In the similar way, the MATLAB function medfilt2(I) that implements the 2D median filter can be used to teach the concept of impulse noise removal. From Figure 6 the influence of salt and pepper noise can be easily understood by observing the black and white pixels. Also it can be comfortably taught as the median filter is conceptually very simple and it exhibits good noise removal performance at low noise densities[4, 7]. This may be explained by comparing the denoised image at 5% noise and 20% noise. In the later, even after denoising some black and white pixels are left unchanged. Thus, it can be easily demonstrated that the simple median filter is not suitable for images corrupted with higher noise densities. In the similar way other variants of median filter such as adaptive median filter, switching median filter, weighted median filter, and directional median filter can be efficiently taught.

Figure 5. Output images and sample code for Gaussian noise removal using average filter

Figure 6. Output images and sample code for Salt & Pepper noise removal using simple median filter

3.2. Teaching Image Segmentation with MATLAB

The very basic type of segmentation called thresholding is classified into two namely single and multiple thresholding (Figure 7 and Figure 8)[4, 9]. Single threshold segment the image into two homogeneous regions which are shown in black and white. In the multiple threshold shown in Figure 8, the image is segmented into three homogeneous regions; the pixels with gray level intensity less than 100 are replaced by 0 (black);the pixels with gray level intensity greater than 100 are replaced by 255 (white); the remaining pixels are assigned the gray level value 150 (light shade of gray). This approach will aid the teacher to teach the thresholding based segmentation in a simplified way[20].

Figure 7. Output images and sample code for simple thresholding based segmentation

Figure 8. Output images and sample code for multiple thresholding based segmentation

3.3. Teaching the Concepts of Edge Detection with MATLAB

Edge detection is a very important area in the field of Computer Vision. The edges define the boundaries between regions in an image; it helps with segmentation and object recognition[4, 20]. They can show where shadows fall in an image or any other distinct change in the intensity of an image. Edge detection is a fundamental of low-level image processing and good edges are necessary for higher level processing[10].

A simple MATLAB code that, demonstrates the Prewitt and Sobel mask for diagonal edge detection, Laplacian mask and Laplacian of Gaussian mask and the corresponding output images are shown in Figure 9. By observing Figure 9, the student can easily understand that the Prewitt and Sobel operators are good in detecting diagonal edges where as the Laplacian and Laplacian of Gaussian are able to detect edges in all directions as a result they give a clear picture of the object boundaries.

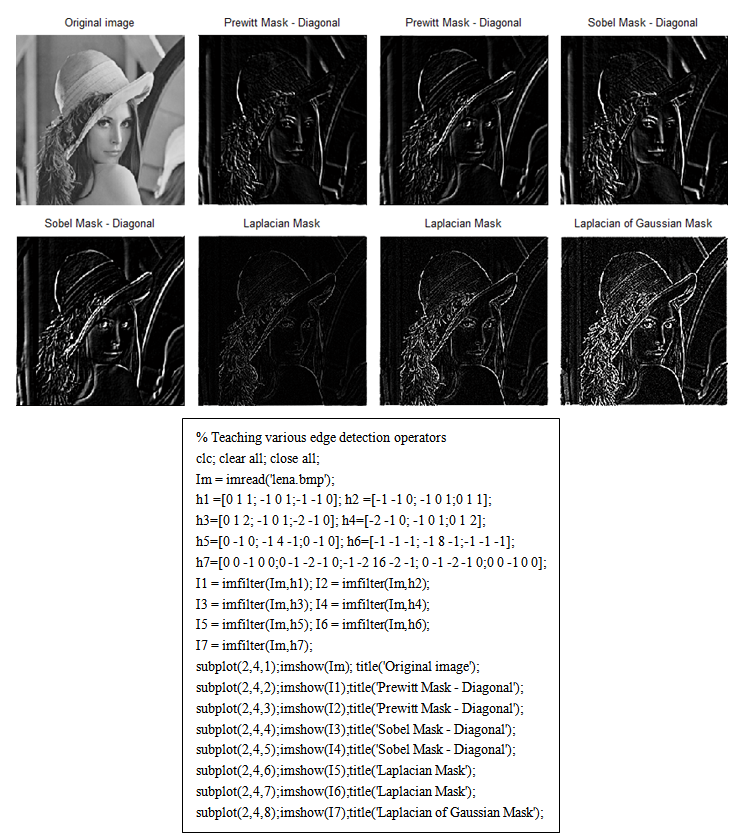Figure 9. Output images and sample code for demonstrating various edge detection operators

4. Conclusions

This article presented a new way of effective teaching method for learning the concepts of image processing using MATLAB. This practised approach is developed for the graduate and undergraduate level students with engineering background. The students can increase the level of understanding of and their performance in easiest way through this approach. This kind of teaching methodology also encourages the students to develop the algorithms and codes with their own idea for implementing various applications. This can ignite and enable the students to think on bringing practical solutions for the problems in engineering and technology. This approach not only gives better understanding of the subject but also enrich the students with better programming skills and analytical thinking ability.

This approach can also be adopted in teaching the concepts of image compression[22], registration, feature extraction, retrieval and other image processing concepts.