T. J. Moir
School of Engineering, AUT University, Auckland, New-Zealand
Correspondence to: T. J. Moir, School of Engineering, AUT University, Auckland, New-Zealand.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The approximate solution to the inverse of a non-minimum phase finite-impulse response (FIR) transfer function is given. Such a problem arises in many areas which include room-acoustics and channel equalisation. Unlike previous work the method does not require multiple sensors or the use of all-pass transfer function networks.
Keywords:
Non-minimum Phase, Inversion, Impulse Response, Signal Processing
Cite this paper: T. J. Moir, Inverting Non-minimum Phase FIR Transfer Functions, American Journal of Signal Processing, Vol. 3 No. 4, 2013, pp. 102-105. doi: 10.5923/j.ajsp.20130304.02.
1. Introduction
FIR transfer functions are more than often the impulse response of a communication channel or acoustic environment found experimentally. In the case of minimum-phase FIR transfer functions their inverse is easily found, but for the non-minimum phase case the inverse becomes unstable. Previous work in the area[1] involves splitting the transfer function into the combination of an all-pass transfer functions and a minimum-phase transfer function. The minimum-phase part is then inverted leaving the all-pass transfer function which has magnitude unity (and hence does not effect the magnitude response of the inverse filter). Provided the group-delay is constant this method is satisfactory. However, as discussed in[1] if the all-pass transfer function does not have constant group-delay then the conventional method will have a noticeable non-linear phase miss-match. The importance of a linear phase solution is that frequencies are scaled by a proportional amount when passing through the channel and filter, thus preserving the shape of the original signal. Linear phase is equivalent to having a pure time-delay (constant group-delay) which will for example introduce no perceptual distortion in a speech signal.The method used here recognises that the inverse of a non-minimum phase impulse-response can either be an unstable system or a stable yet uncausal system. The uncausal part is then used by employing a time-delay and shifting this part back into positive time. Unfortunately the uncausal impulse response has an infinite impulse response so it must truncated making the method approximate depending on the length of the delay. This method is not new in principle, having been used for decades in adaptive filtering using least-mean squares (LMS) algorithms[2, 3]. In audio acoustics, the equalization of loudspeaker characteristics faces similar problems[4] and in sound rendering[5]. In the control literature similar problems are often encountered[6]. Techniques already exist for two or more sensors[7], but this explicit solution is new and only requires one signal-transmission channel.
2. Mathematical Preliminaries
If a polynomial defined as 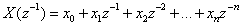 of degree n with real coefficients has all its roots within the unit circle in the z plane, then it is termed strict sense minimum phase. No zeros are assumed to be on the unit circle. For simplicity
of degree n with real coefficients has all its roots within the unit circle in the z plane, then it is termed strict sense minimum phase. No zeros are assumed to be on the unit circle. For simplicity 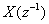 is often written as
is often written as  , omitting the complex argument
, omitting the complex argument 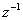 . The conjugate polynomial
. The conjugate polynomial 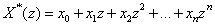 is strict sense non-minumum phase having all of its roots outside the unit circle on the z plane. The reciprocal polynomial is defined as
is strict sense non-minumum phase having all of its roots outside the unit circle on the z plane. The reciprocal polynomial is defined as 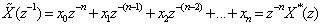 which has all its roots outside the unit circle provided
which has all its roots outside the unit circle provided 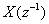 is strict sense minimum phase. The zeros of
is strict sense minimum phase. The zeros of 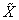 are the zeros of
are the zeros of 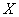 reflected in the unit circle. Similarly
reflected in the unit circle. Similarly 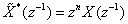 has all its roots within the unit circle. For polynomials which are strict sense non-minimum phase, we can factorise
has all its roots within the unit circle. For polynomials which are strict sense non-minimum phase, we can factorise 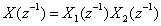 where
where 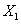 is strict sense minimum phase and
is strict sense minimum phase and 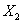 is strict sense non-minimum phase.
is strict sense non-minimum phase.
3. Theory
Begin with the FIR transfer functionof a transmission channel as described by the product of two polynomials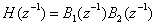 | (1) |
where [8] 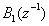 is strict sense minimum phase and
is strict sense minimum phase and 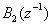 is strict sense non-minimum phase. Their polynomial dimensions are
is strict sense non-minimum phase. Their polynomial dimensions are 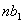 and
and 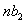 respectively.We require an inverse transfer-function
respectively.We require an inverse transfer-function 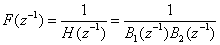 | (2) |
To proceed further we note that 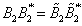 and substitute
and substitute 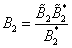 into (2) giving
into (2) giving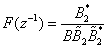 | (3) |
Now the reciprocal polynomial 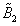 is stable having all of its roots within the unit circle, but
is stable having all of its roots within the unit circle, but 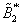 is not. Therefore expand in positive powers of z
is not. Therefore expand in positive powers of z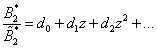 | (4) |
For a non-minimum phase polynomial 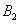 of degree
of degree 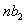 the expansion (4) is easily found by a simple recursion. For example if
the expansion (4) is easily found by a simple recursion. For example if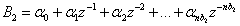 | (5) |
then 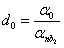
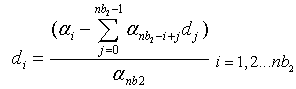 | (6) |
and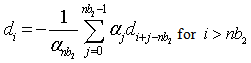 | (7) |
Delaying by 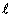 terms
terms 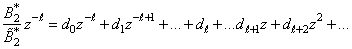 | (8) |
Which is a Laurent series with negative (causal) and positive (uncasual) powers of z.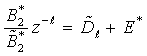 | (9) |
The reciprocal polynomial 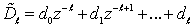 , whereas
, whereas 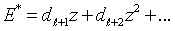 is an infinite polynomial. However, if the delay is large enough we can approximate
is an infinite polynomial. However, if the delay is large enough we can approximate 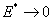 since this is part of a convergent power-series whose higher terms will converge to zero. So (3) becomes
since this is part of a convergent power-series whose higher terms will converge to zero. So (3) becomes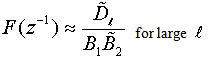 | (10) |
which is the inverse filter. It would be possible of course to express this as an FIR transfer function by using polynomial division and further truncation.
4. Example
Consider an FIR transfer function with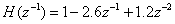 or
or 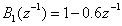 and
and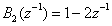 . Find its inverse and use a delay of
. Find its inverse and use a delay of 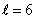 .Solution:Use the fact that
.Solution:Use the fact that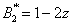 ,
,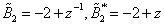 . Now expand
. Now expand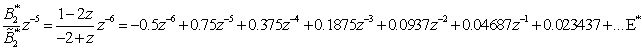 So that
So that 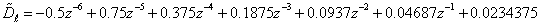 Substituting into (10) we find the inverse transfer function as
Substituting into (10) we find the inverse transfer function as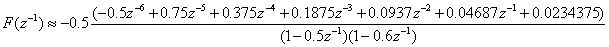 For comparison purposes we use the alternative approach [1] which employs an all-pass transfer function.
For comparison purposes we use the alternative approach [1] which employs an all-pass transfer function.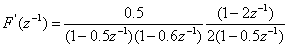 Now when the original channel transfer-function
Now when the original channel transfer-function 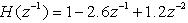 is applied by convolution with the inverse filter, unity gain should be achieved up to half-sampling frequency. A comparison of the magnitude and phase inverse transfer functions are shown in Figs 1 and 2 respectively. Fig 1 shows a comparison for different values of delay showing that the amount of ripple reduces considerably as the delay increases.
is applied by convolution with the inverse filter, unity gain should be achieved up to half-sampling frequency. A comparison of the magnitude and phase inverse transfer functions are shown in Figs 1 and 2 respectively. Fig 1 shows a comparison for different values of delay showing that the amount of ripple reduces considerably as the delay increases.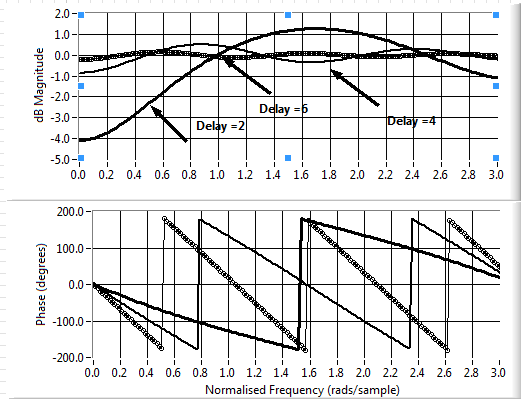 | Figure 1. Magnitude and phase of equalised impulse response using new method |
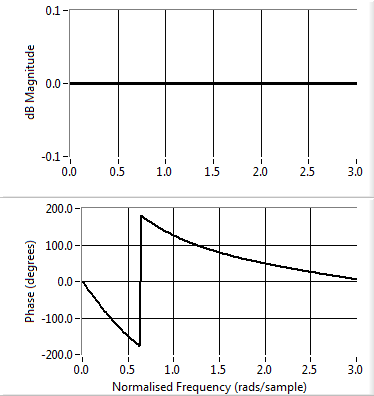 | Figure 2. Magnitude and phase of equalised response using all-pass method |
It can be seen that there is some 0.5dB peak-to peak ripple in the magnitude for the new case when the delay is 4 whilst for the all-pass method the magnitude is perfectly flat. However, the phase for the all-pass method is non-linear whereas for the new method the phase is linear. Furthermore the ripple for the new method is further reduced by making the delay term bigger. For example, for a delay of 6 samples the dB ripple is down to 0.1dB peak-to peak whilst still maintaining linear phase.
5. Conclusions
A single sensor approach to the inversion of non-minimum phase FIR transfer functions has been shown. The method is computationally simple and does not rely on all-pass transfer functions. Instead, it uses the uncausal part of the transfer function inverse itself which is shifted into positive time by using a time-delay. This gives rise to an equalised transfer function which has a small amount of ripple yet is linear phase. For small impulse responses it becomes quite an easy task to find the inverse and this is of some theoretical importance, However, for much larger impulse responses which could be met in an acoustic environment,the method requires the factorization of large polynomials into minimum and non-minimum phase polynomials, which is in itself quite a computational task. Therefore an efficient computational algorithm needs to be found for performing this task without having to find all of the individual roots of the polynomials themselves.
References
| [1] | S. T. Neely and J. B. Allen, "Invertibility of a room impulse response," J.Acoust.Soc.Amer., vol. 66, pp. 165-169, 1979. |
| [2] | S. Haykin, Adaptive filter theory. Englewood Cliffs New Jersey: Prentice Hall, 1986. |
| [3] | B. Widrow and M. Bilello, "Adaptive Inverse Control," presented at the Proceedings of the 1993 International Symposium on Intelligent Control, Chicago,Illinois USA, 1993. |
| [4] | A. Marques and D. Freitas, "Infinite impulse response (IIR) inverse filter design for the equalization of non-minimum phase loudspeaker systems," in Applications of Signal Processing to Audio and Acoustics, 2005. IEEE Workshop on, 2005, pp. 170-173. |
| [5] | A. Mouchtaris, P. Reveliotis, and C. Kyriakakis, "Non-minimum phase inverse filter methods for immersive audio rendering," in Acoustics, Speech, and Signal Processing, 1999. Proceedings., 1999 IEEE International Conference on, 1999, pp. 3077-3080 vol.6. |
| [6] | B. Widrow and M. Bilello, "Adaptive inverse control," in Intelligent Control, 1993., Proceedings of the 1993 IEEE International Symposium on, 1993, pp. 1-6. |
| [7] | M. Miyoshi and Y. Kaneda, "Inverse filtering of room acoustics," Acoustics, Speech, and Signal Processing [see also IEEE Transactions on Signal Processing], IEEE Transactions on, vol. 36, pp. 145-152, 1988. |
| [8] | T. J. Moir, "A z-domain transfer function solution to the non-minimum phase acoustic beamformer," Intern. J. Syst. Sci., vol. 38, pp. 563-575, 2007. |

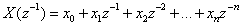 of degree n with real coefficients has all its roots within the unit circle in the z plane, then it is termed strict sense minimum phase. No zeros are assumed to be on the unit circle. For simplicity
of degree n with real coefficients has all its roots within the unit circle in the z plane, then it is termed strict sense minimum phase. No zeros are assumed to be on the unit circle. For simplicity 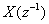 is often written as
is often written as 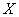 , omitting the complex argument
, omitting the complex argument 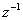 . The conjugate polynomial
. The conjugate polynomial 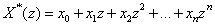 is strict sense non-minumum phase having all of its roots outside the unit circle on the z plane. The reciprocal polynomial is defined as
is strict sense non-minumum phase having all of its roots outside the unit circle on the z plane. The reciprocal polynomial is defined as 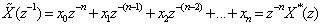 which has all its roots outside the unit circle provided
which has all its roots outside the unit circle provided 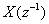 is strict sense minimum phase. The zeros of
is strict sense minimum phase. The zeros of 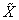 are the zeros of
are the zeros of 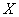 reflected in the unit circle. Similarly
reflected in the unit circle. Similarly 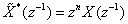 has all its roots within the unit circle. For polynomials which are strict sense non-minimum phase, we can factorise
has all its roots within the unit circle. For polynomials which are strict sense non-minimum phase, we can factorise 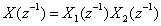 where
where 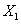 is strict sense minimum phase and
is strict sense minimum phase and 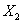 is strict sense non-minimum phase.
is strict sense non-minimum phase.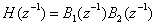
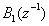 is strict sense minimum phase and
is strict sense minimum phase and 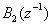 is strict sense non-minimum phase. Their polynomial dimensions are
is strict sense non-minimum phase. Their polynomial dimensions are 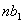 and
and 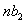 respectively.We require an inverse transfer-function
respectively.We require an inverse transfer-function 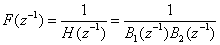
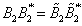 and substitute
and substitute 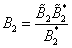 into (2) giving
into (2) giving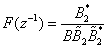
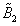 is stable having all of its roots within the unit circle, but
is stable having all of its roots within the unit circle, but 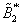 is not. Therefore expand in positive powers of z
is not. Therefore expand in positive powers of z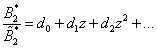
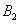 of degree
of degree 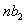 the expansion (4) is easily found by a simple recursion. For example if
the expansion (4) is easily found by a simple recursion. For example if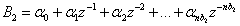
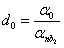
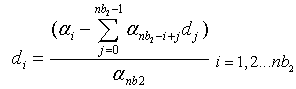
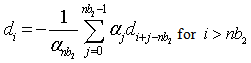
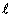 terms
terms 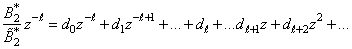
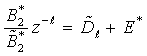
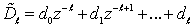 , whereas
, whereas 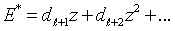 is an infinite polynomial. However, if the delay is large enough we can approximate
is an infinite polynomial. However, if the delay is large enough we can approximate 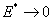 since this is part of a convergent power-series whose higher terms will converge to zero. So (3) becomes
since this is part of a convergent power-series whose higher terms will converge to zero. So (3) becomes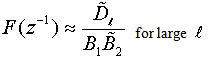
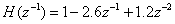 or
or 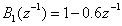 and
and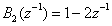 . Find its inverse and use a delay of
. Find its inverse and use a delay of 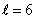 .Solution:Use the fact that
.Solution:Use the fact that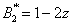 ,
,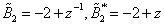 . Now expand
. Now expand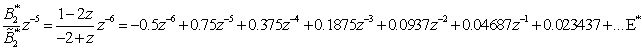 So that
So that 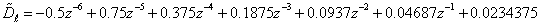 Substituting into (10) we find the inverse transfer function as
Substituting into (10) we find the inverse transfer function as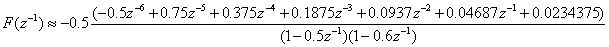 For comparison purposes we use the alternative approach [1] which employs an all-pass transfer function.
For comparison purposes we use the alternative approach [1] which employs an all-pass transfer function.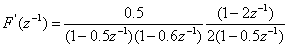 Now when the original channel transfer-function
Now when the original channel transfer-function 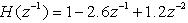 is applied by convolution with the inverse filter, unity gain should be achieved up to half-sampling frequency. A comparison of the magnitude and phase inverse transfer functions are shown in Figs 1 and 2 respectively. Fig 1 shows a comparison for different values of delay showing that the amount of ripple reduces considerably as the delay increases.
is applied by convolution with the inverse filter, unity gain should be achieved up to half-sampling frequency. A comparison of the magnitude and phase inverse transfer functions are shown in Figs 1 and 2 respectively. Fig 1 shows a comparison for different values of delay showing that the amount of ripple reduces considerably as the delay increases.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML