-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2013; 3(3): 54-70
doi:10.5923/j.ajsp.20130303.03
Analysis of Wavelet Transform-Domain LMS-Newton Adaptive Filtering Algorithms with Second-Order Autoregressive (AR) Process
Tanzila Lutfor , Md. Zahangir Alam , Sohag Sarker
School of Science and Engineering (SSE), UITS, Dhaka, Bangladesh
Correspondence to: Tanzila Lutfor , School of Science and Engineering (SSE), UITS, Dhaka, Bangladesh.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper analyze the stability, misadjustment, and convergence performance of the Wavelet Transform (WT) domain least mean square (LMS) Newton adaptive filtering algorithm with first order and second order autoregressive (AR) process. The wavelet transform domain signal provides a means of constructing of more orthonormal correlated input signals than other transform. The wiener filter with AR input process are assumed to be stationary, and the Stationary Wavelet Transform (SWT) is used as transform algorithm to provide more correlated input signal than other integral transform. The simulation result of this work shows that Wavelet-domain LMS-Newton algorithm provides better performance result than other transform domain algorithm for both first order and second order AR process. Structure of the SWT based LMS-Newton adaptive algorithm for time-varying process has been also discussed in this paper. Finally, Computer simulations on the SWT based LMS-Newton adaptive algorithms are demonstrated to validate the analysis presented in this paper, and the simulation result shows that the structure of SWT domain LMS-Newton adaptive algorithm provides better denoising of a noisy signal than other transform domain LMS-Newton adaptive algorithm.
Keywords: Discrete Fourier Transform, Discrete Cosine Transform, Least Mean Square (LMS) Algorithm, Stationary Wavelet Transform (SWT), Autoregressive (AR) Process
Cite this paper: Tanzila Lutfor , Md. Zahangir Alam , Sohag Sarker , Analysis of Wavelet Transform-Domain LMS-Newton Adaptive Filtering Algorithms with Second-Order Autoregressive (AR) Process, American Journal of Signal Processing, Vol. 3 No. 3, 2013, pp. 54-70. doi: 10.5923/j.ajsp.20130303.03.
Article Outline
1. Introduction
- The computation complexity of the time-domain adaptive filtering algorithms such as LMS algorithms, gradient adaptive lattice, and Least Square algorithms increases linearly with the filter order[1]-[4], and it is difficult to use such filter in high speed real time applications[5]. The frequency domain LMS algorithms using fast Fourier Transform (FFT) reduces the number of mathematical computations and the orthogonal transform provides more computation counts[6]-[8]. The convergence rate depends on the input autocorrelation matrix and decreases radically with higher input correlation. The transform domain algorithms updated the filter coefficients that can be applied for the case of higher input correlation to obtain higher convergence rate[9][10]. The transform domain adaptive filter achieved rapid convergence of the filter coefficients for non-white input signal with a reasonably lower computational complexity than simpler LMS based system. The gradient based LMS algorithm having convergence rate dependency on the input signal statistics but the LMS-Newton (LMSN) algorithm is another powerful alternatives for larger eigenvalue spread of the input correlation matrix. The step size (μ) of LMS and the reference signal power play an important role in the stability and convergence of the LMS adaptation process. The fixed value of μ responds to stationary channel, and for the time-varying channel variable step-size LMS algorithm has been proposed to obtain better performance for non-stationary channel[11]-[13]. The Normalized LMS (NLMS) uses variable step-size (μ) algorithm to optimize convergence speed, stability, and performance. The time-variable step-size (μ) is implemented based on the power estimation of the input signals[14]. The larger μ is used for non-stationary and smaller μ is used for stationary without considering the convergence rate[15][16]. Further, modification on NLMS is proposed named as VS-NLMS in which μ is decided by the estimation of input signals, and it achieves a faster convergence rate with maintaining the stability of the NLMS[17]. The proposed VS-LMS with time-varying step-size (μ) improves the output signal to noise ratio (SNR) and the convergence speed. A new type of criteria is proposed using output error with step-size value (μ) from a big value α2 and smaller one α1 to provide faster tracing speed and smallermisadjustment[18]-[20]. The stability and convergence properties of transform - domain LMS algorithm has been investigated in[21], the authors also analyzed the effects of the transforms and power normalization in various adaptive filters for both first order and second order AR process. In the same work they stated that the power normalization increases the difficulty for analyzing the stability and convergence performance. The LMS-Newton algorithm avoids the slow convergence of the LMS algorithm for highly correlated input signal[15], this property should be very useful in DWT-LMS algorithm and is used in this work.In[21]-[23], the authors analyze the transform-domain adaptive filters with discrete Fourier transform (DFT), discrete Cosine transform (DCT), discrete Hartely transform (DHT), and discrete Sine transform (DST) for first-order and second-order AR input process with their stabilities and convergence performance for input power normalization. The result of the work[24] shows that the DCT-LMS and DST-LMS provides the better convergence performance for both first and second order AR process than the DFT-LMS and DHT-LMS. In this paper, we analyze the Discrete Wavelet Transform (DWT) in adaptive filtering algorithm in form as DWT-LMS Newton adaptive filters for both first order and second order AR process to enhance Misadjustment to measure the steady-state convergence, and MSE performance. This paper also discuss the design of the DWT-LMS for the time-varying AR process, the time-varying block by block basis data is processed by using ε-decimated DWT algorithm. The simulation study in our work shows that SWT-LMS Newton adaptive filter provides better stability, misadjustment, and convergence performances than that of DFT-LMS and DCT-LMS for both first order and second order AR process[23].
2. Analytical Form of Transform-Domain LMS-Newton Algorithm
- The LMS-Newton algorithm estimates the second order statistics of the wide-sense stationary signal. The algorithm avoids the slow convergence of the LMS algorithm for highly correlated input signal. The LMS-Newton algorithm minimized the MSE at instant (n+1) if[15]
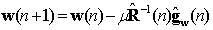 | (1) |
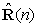 is the estimation of the auto-correlation matrix, namely, R≈E[u(n)uH(n)], u(n) is the input signal vector. The unbiased estimate of R for stationary input signal is as:
is the estimation of the auto-correlation matrix, namely, R≈E[u(n)uH(n)], u(n) is the input signal vector. The unbiased estimate of R for stationary input signal is as: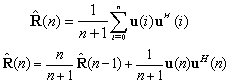 | (2) |
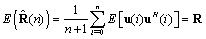 | (3) |
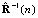 that is required for LMS-Newton algorithm can be given using the Matrix inverse Lemma as[21]:
that is required for LMS-Newton algorithm can be given using the Matrix inverse Lemma as[21]: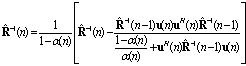 | (4) |
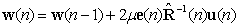 | (5) |
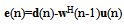 | (6) |
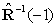 =δI (δ is positive constant less than 0, and I is unity matrix); w (0) =[0 0 0 . . . . . . .]TThe transform domain LMS transformed the input signal vector u(n) in a more convenient vector s(n), s(n)=Tu(n), where TTH=I, the transform matrix of following form as:
=δI (δ is positive constant less than 0, and I is unity matrix); w (0) =[0 0 0 . . . . . . .]TThe transform domain LMS transformed the input signal vector u(n) in a more convenient vector s(n), s(n)=Tu(n), where TTH=I, the transform matrix of following form as: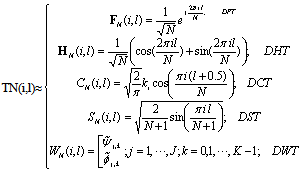 | (7) |
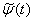 and
and 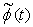 are wavelet function and scaling function respectively. The autocorrelation matrix for the transform-domain input signal vector s(n) is given by:
are wavelet function and scaling function respectively. The autocorrelation matrix for the transform-domain input signal vector s(n) is given by: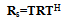 | (8) |
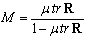 | (9) |
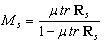 | (10) |
3. Wavelet Packet Transform Based LMS Algorithm
- The wavelet packet transform of the signal x(n) can denoted as[25][26]:
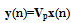 | (11) |
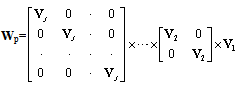 | (12) |
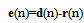 | (13) |
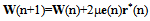 | (14) |
3.1. Algorithm Performance Analysis
- The cross-correlation vector Py between the desired signal d(n) and the wavelet packet transform signal y(n) is as:
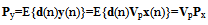 | (15) |
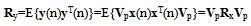 | (16) |
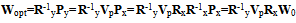 | (17) |
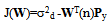 | (18) |
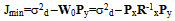 | (19) |
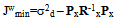 | (20) |
3.2. Convergence Analysis of Wavelet Transform Domain LMS Adaptive Filter with AR Process
- AR(P) model for univariate time series are Markov process, and Pth order AR process to generate the data yt is as:
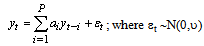 | (21) |
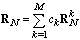 | (22) |
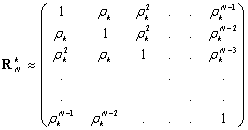 | (23) |
3.2.1. Eigenvalue Spread for First Order AR Process
- The first order Markov signals can be obtained by passing a white noise through a one-pole low-pass filter. The N by N autocorrelation matrix of AR (1) or Markov-1 process is obtained from (23) as:
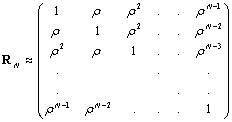 | (24) |
 in the wavelet domain for AR (1) process is the autocorrelation matrix of the Markov-1 process of the wavelet transform domain input signal of the same parameter ρ that is:
in the wavelet domain for AR (1) process is the autocorrelation matrix of the Markov-1 process of the wavelet transform domain input signal of the same parameter ρ that is:  ; where W is the N×N order wavelet transform matrix. Now, putting the value of the wavelet transform matrix from (B. 10) of appendix-B, we have the following form as:
; where W is the N×N order wavelet transform matrix. Now, putting the value of the wavelet transform matrix from (B. 10) of appendix-B, we have the following form as: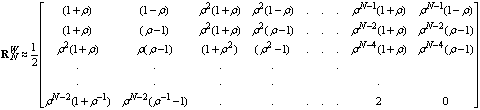 | (25) |
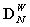 defined by the first row of (25) as:
defined by the first row of (25) as: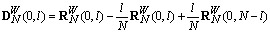 | (26) |
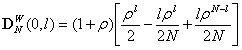 | (27) |
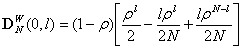 | (28) |
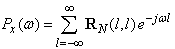 | (29) |
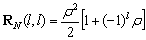 . Now, from (29) we have the power spectrum of the form as:
. Now, from (29) we have the power spectrum of the form as: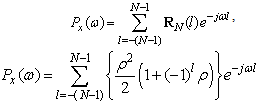 | (30) |
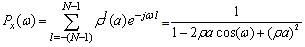 Again considering ρ1=ρa, we have above equation in the following form as:
Again considering ρ1=ρa, we have above equation in the following form as: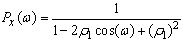 | (31) |
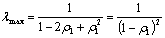 | (32) |
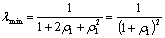 | (33) |
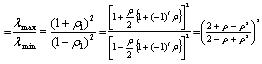 | (34) |
3.2.2. Eigenvalue Spread for Second Order AR Process
- The characteristic equation for second order AR (2) process is given as[32]:
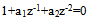 | (35) |
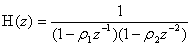 | (36) |
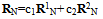 | (37) |
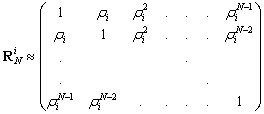 | (38) |
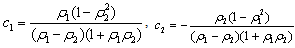 | (39) |
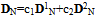 | (40) |
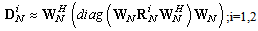 | (41) |
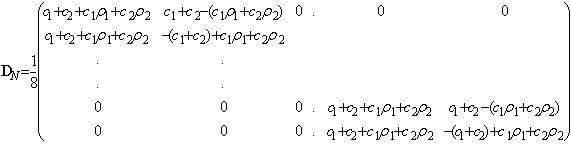 | (42) |
 | (43) |
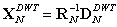 | (44) |
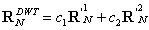 | (45) |
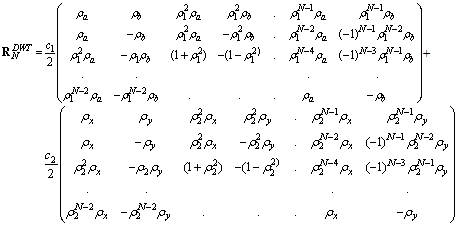 | (46) |
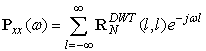 | (47) |
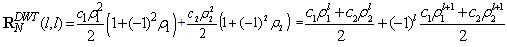 | (48) |
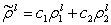 ; l=0, 1, , N-1, the (50) can be written as:
; l=0, 1, , N-1, the (50) can be written as: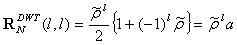 | (49) |
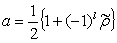 . Now, (50) can be written as:
. Now, (50) can be written as: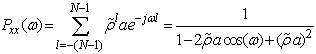 | (50) |
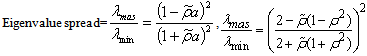 | (51) |
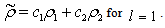
4. Structure of Wavelet Transform LMS Algorithm
- Signal in most of engineering applications are non-stationary, and Fourier transform encountered difficulty to analyze the time-frequency property[33][34]. The wiener filter is assumed to be stationary but the stationary assumption of the noisy signal cannot completely satisfied in many applications[35]. The SWT domain signal vector v(k) in the matrix form can be expressed as:
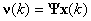 | (52) |
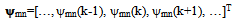 | (53) |
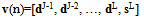 | (54) |
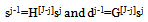 | (55) |
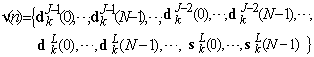 | (56) |
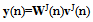 | (57) |
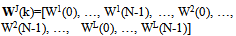 | (58) |
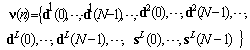 | (59) |
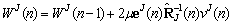 | (60) |
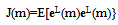 | (61) |
5. Result
- The misadjustment of the adaptive filter measures the amount of noise in the filter output and increases with the step-size parameter. Lower amount of misadjustment indicates the better denoising performance of the filtering algorithm. Let us consider a multi-tone signal of the following form as:
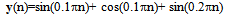 | (62) |
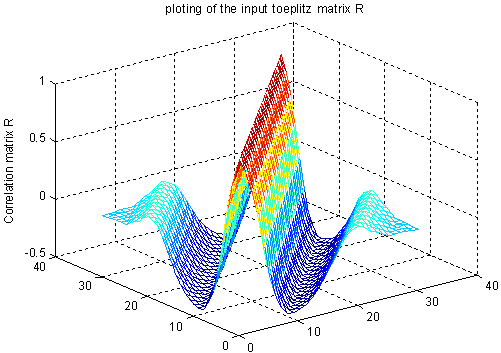 | Figure 1(a). Autcorrelation matrix of the input multi-tone signal without any tranformation |
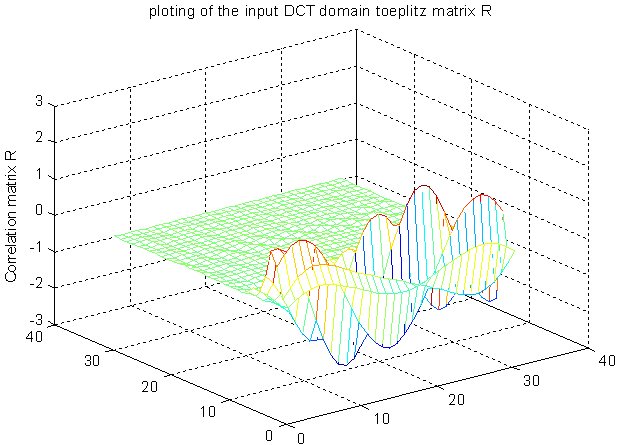 | Figure 1(b). Autocorrelation matrix of the DCT transformed based multi-tone signal |
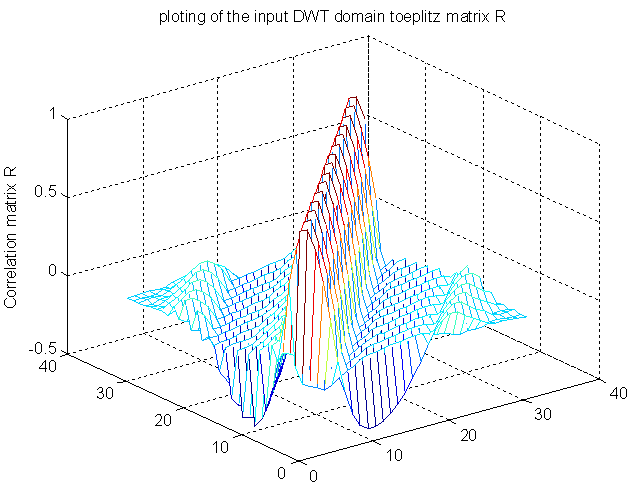 | Figure 1(c). DWT based autocorrelation matrix of the input multi-tone signal |
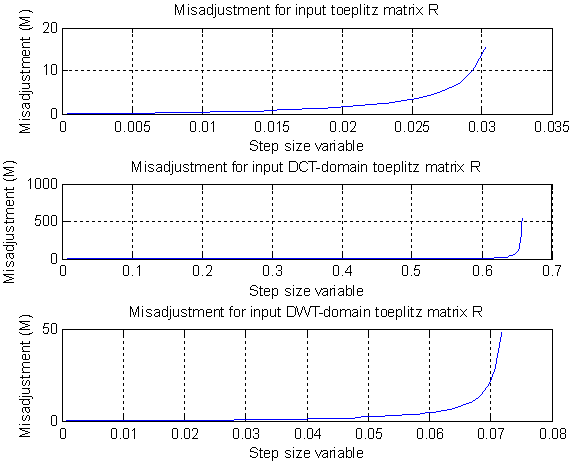 | Figure 1(d). Misadjustment result of input autocorrelation matrix, DCT and DWT based input autocorrelation matrix |
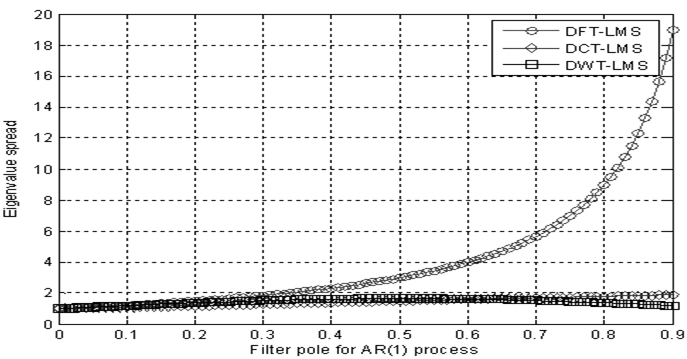 | Figure 2. Eigenvalue spread of DFT-LMS, DCT-LMS, and DWT-LMS for AR (1) input process |
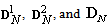 in (41) and (40) after applying DWT in the input AR(2) process is shown in Fig. 4(b), Fig. 4(c), and Fig. 4(d) respectively. Now, we compute the matrix
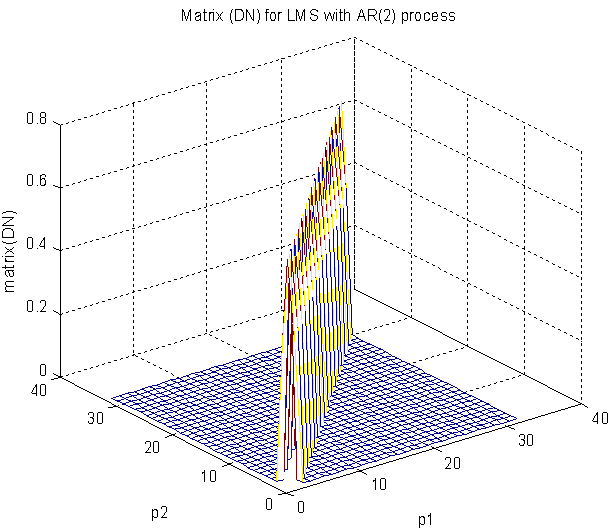
in (41) and (40) after applying DWT in the input AR(2) process is shown in Fig. 4(b), Fig. 4(c), and Fig. 4(d) respectively. Now, we compute the matrix 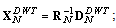 where RN is given in (37) and
where RN is given in (37) and 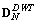 is given in (43) and plotted in Fig. 4(d). The distribution of
is given in (43) and plotted in Fig. 4(d). The distribution of 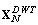 is shown in Fig. 5(a) for the sample value of N=30, the result shows that most elements of
is shown in Fig. 5(a) for the sample value of N=30, the result shows that most elements of 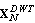 is very close to zero and the only the diagonal elements having values close to 0.6. The distribution of
is very close to zero and the only the diagonal elements having values close to 0.6. The distribution of 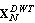 is very important factor to compute the eigenvalue spread of the autocorrelation matrix VN; that obtained after DWT.
is very important factor to compute the eigenvalue spread of the autocorrelation matrix VN; that obtained after DWT.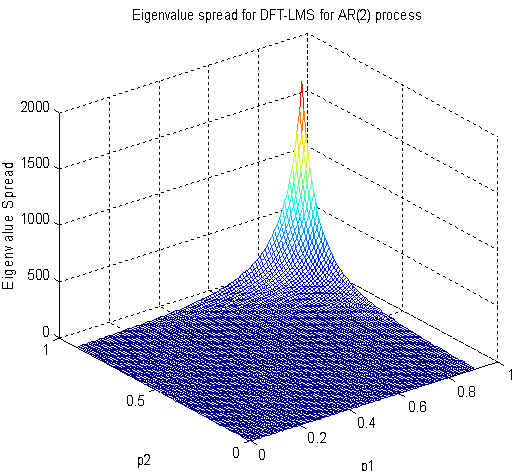 | Figure 3(a). Eigenvalue spread of DFT-LMS for second-order lowpass AR process |
 | Figure 3(b). Eigenvalue spread of DCT-LMS for second-order lowpass AR process |
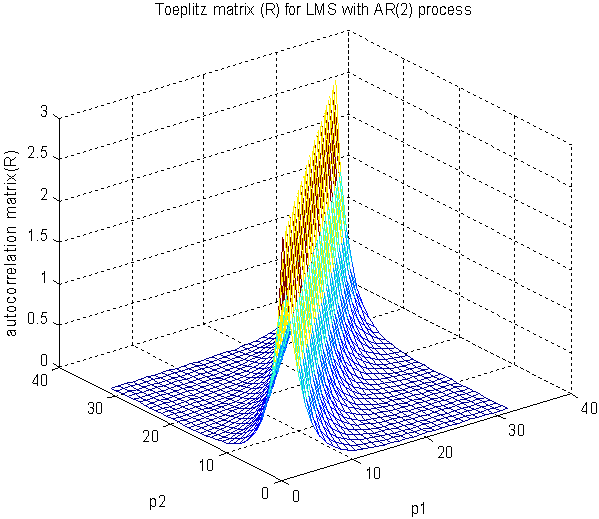 | Figure 4(a). Autocorrelation matrix RN before any transform for AR(2) input process |
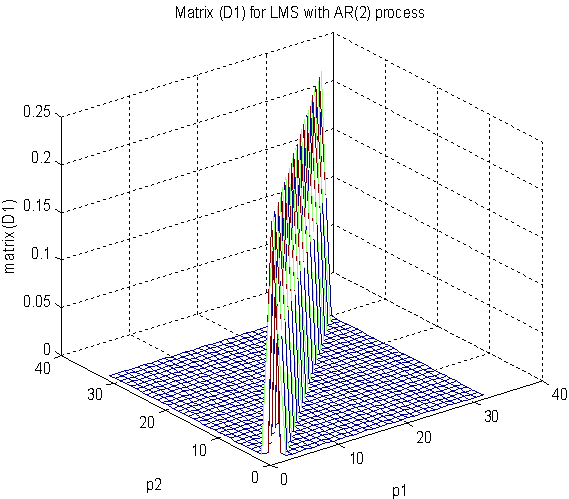 | Figure 4(b). Matrix  after DWT in the AR(2) process after DWT in the AR(2) process |
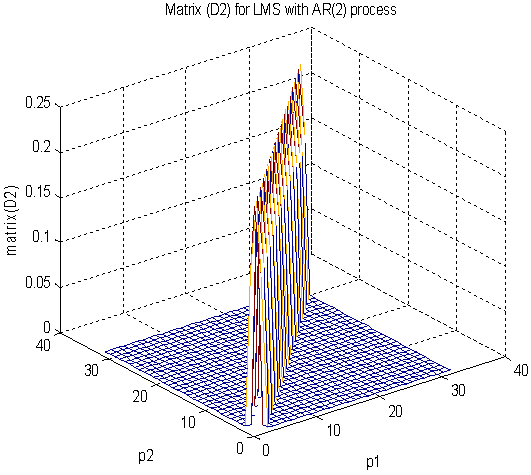 | Figure 4(c). Matrix 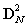 after DWT in the AR (2) process after DWT in the AR (2) process |
 | Figure 4(d). Matrixn DN after DWT in the AR(2) process |
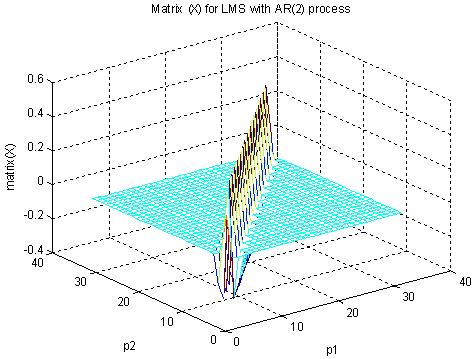 | Figure 5(a). 3D plot of the matrix 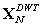 involved in DWT-LMS eigenvalue spread calculation involved in DWT-LMS eigenvalue spread calculation |
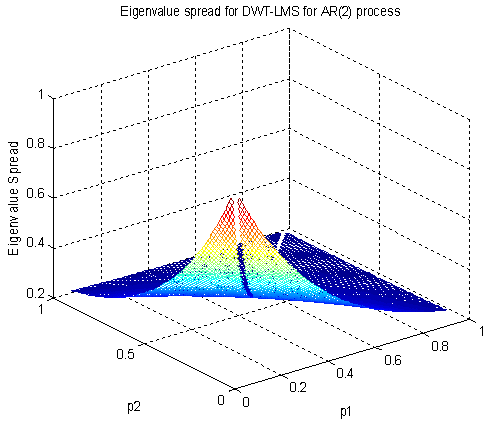 | Figure 5(b). Eigenvalue spread of DWT-LMS for second-order lowpass AR process |
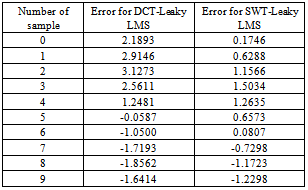
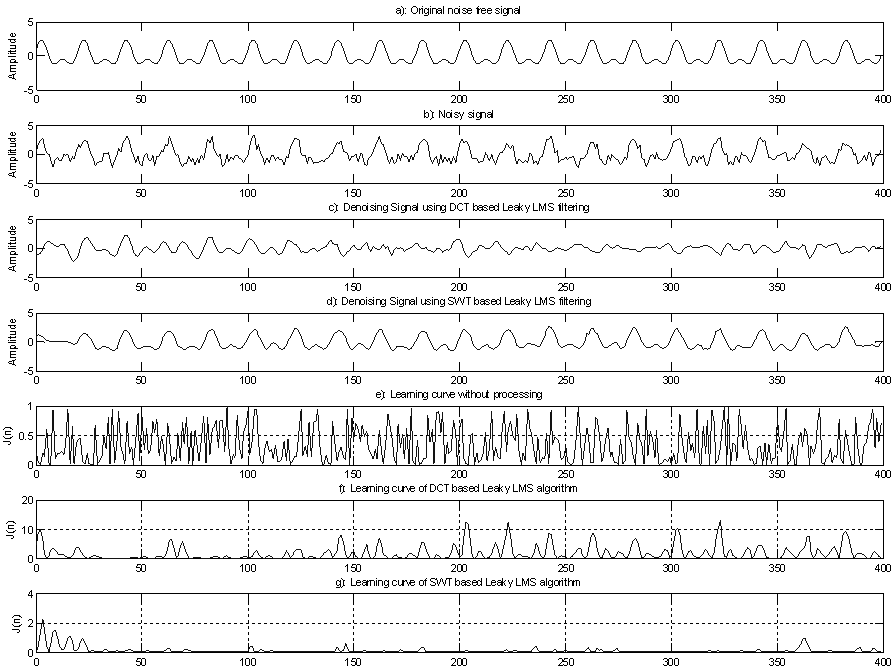 | Figure 6. Denoising performance of DCT-Leaky LMS and SWT-Leaky LMS for AR(2) process |
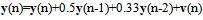 | (63) |
|
6. Conclusions
- The stability and convergence performance of DFT-LMS, DCT-LMS, DHT-LMS, and DST-LMS has been analyzed in details in work[25], and the result shows that DCT-LMS and DHT provides better convergence performance than other. In this work, we have designed DWT-LMS Newton adaptive or SWT-LMS Newton adaptive, or in simply DWT-LMS or SWT-LMS adaptive filtering algorithm and the performances is compared with the DCT-LMS adaptive filtering algorithm for first-order and second-order AR process as developed in the early work[25]. From the comparison result it is shown that DWT-LMS provides better misadjustment, convergence,and denoisingperformance than that of DCT-LMS adaptive filtering algorithm for both AR(1) and AR(2) process. For example, if ρ=0.8 then eigenvalue spread of DCT-LMS is 1.8 and for DWT-LMS is 1.37 for AR(1) process. The eigenvalue spread of DCT-LMS is 2.63 and for DWT-LMS is 0.25 for ρ1=0.59 and ρ2= 0.79 respectively with AR(2) process. From talble-1, it is also concluded that SWT-LMS provides less denoising error in each sample value than DCT-LMS adaptive algorithm. Hence, the DWT-LMS provides better misadjustment, convergence or eigenvalue spread, and denoising performance than others as presented in work[25]. In future the SWT-LMS algorithm can be applied for higher order AR process and other type of input process like MA and ARMA process.
APPENDIX A: MSE of Wavelet Packet Domain Signal
- J(W)=E{e2(n)}=E{[d(n) −r(n)]2}=E{[d(n)-WT(n)y(n)]2} The error function in wavelet domain can be written by replacing the input signal in wavelet transform domain as:
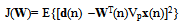 | (A.1) |
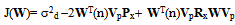 | (A.2) |
APPENDIX B: Algorithm in Generating a Wavelet Matrix
- Let us assume W be an N by N matrix of the following form:
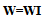 | (B.1) |
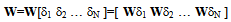 | (B.2) |
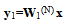 | (B.3) |
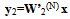 | (B.4) |
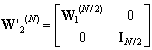 | (B.5) |
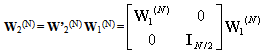 | (B.6) |
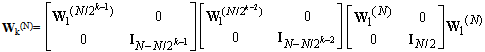 | (B.7) |
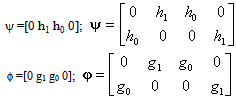 The first scale matrix W1(N) can be written in the form as:
The first scale matrix W1(N) can be written in the form as: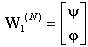 | (B.8) |
 | (B.9) |
 | (B.10) |
APPENDIX C: Determination of Wavelet Domain Auto Correlation Matrix with AR(2) Process
- Using (B.10) and (39), we have
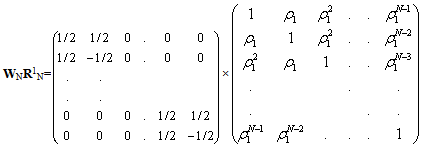 | (C.1) |
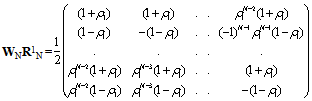 | (C.2) |
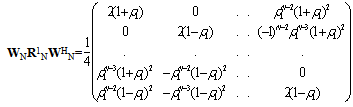 | (C.3) |
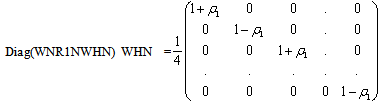 | (C.4) |
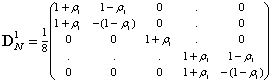 | (C.5) |
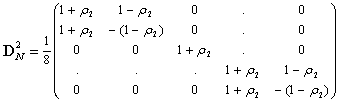 | (C.6) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML