-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2013; 3(2): 25-34
doi:10.5923/j.ajsp.20130302.02
A Comparaison of Methods for Detection of High Frequency Oscillations (HFOs) in Human Intacerberal EEG Recordings
Sahbi Chaibi1, Tarek Lajnef1, Zied Sakka1, Mounir Samet1, Abdennaceur Kachouri1, 2
1Sfax University, National Engineering School of Sfax, LETI Laboratory, ENIS BPW 3038- Sfax, Tunisia
2Gabes University, ISSIG: Higher Institute of Industrial Systems, Gabes CP 6011, Tunisia
Correspondence to: Sahbi Chaibi, Sfax University, National Engineering School of Sfax, LETI Laboratory, ENIS BPW 3038- Sfax, Tunisia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
High Frequency Oscillations (HFOs) in the range of 80-500Hz seem to be a reliable biomarker of tissue capable of producing seizures. Visual marking of HFOs related to long duration/multi channel EEG data is extremely tedious, highly time-consuming and inevitably subjective. Therefore, automated and reliable detection of HFOs is much more efficient. The purpose of the present study is to improve in the first stage three existing HFOs detectors (CMV, MP, BMT), and subsequently compare them on the same database. Our main findings are summarized as follows: The efficiency of methods depends on the required sensitivity and the False Discovery Rate (FDR). First, if the required sensitivity below 87% is sufficient for the intended application, CMV method could perform well in terms of low false detection rate (FDR<14%). Secondly, if the application requires a sensitivity between 87% and 92%, the three methods could perform in a similar way in terms of performance, which approximately corresponds to an FDR in the range of 14-19%. Finally, if a high sensitivity is required (92% up to 98%), BMT based method can be considered the most efficient and leads to significantly lower FDR values (19% to 23%) compared to other methods.
Keywords: Epilepsy, High frequency oscillations (HFOs), Intracereberal Electroencephalography (iEEG), Complex MORLET wavelet (CMW), Matching Pursuit (MP), Bumps Modeling Technique (BMT)
Cite this paper: Sahbi Chaibi, Tarek Lajnef, Zied Sakka, Mounir Samet, Abdennaceur Kachouri, A Comparaison of Methods for Detection of High Frequency Oscillations (HFOs) in Human Intacerberal EEG Recordings, American Journal of Signal Processing, Vol. 3 No. 2, 2013, pp. 25-34. doi: 10.5923/j.ajsp.20130302.02.
Article Outline
1. Introduction
- High frequency oscillation (HFO) is a short rhythmic brain wave consisting of at least three oscillations in the frequency range 80-500Hz[1], and can be clearly distinguished from background activities[2]. HFOs are divided into Ripples 80-250Hz and Fast Ripples (FRs) 250-500Hz[1,2,3,4,5,6]. HFOs can be recorded with invasive EEG procedure using commercial subdural grid/strip and depth electrodes. Invasive EEG can give an accurate reading of neural activities recorded at the brain surface level and within the brain volume[7] for patients with intractable epilepsy. Recent studies reported that HFOs bursts in the band of 40-200Hz[8] and 80-150Hz[9] can also be recorded on the scalp EEG.HFOs are more specific and accurate than spikes/sharp waves to delineate the seizure onset zone (SOZ)[6,10]. HFOs were discovered in epileptic rats and patients with epilepsy[1,3,4] and may be encountered under physiological [11] or under pathological conditions[6,11]. It has been reported that a large proportion of HFOs co-occur with spikes[5], and can also occur independently in non spiking channels[6,12]. Postsurgical study[13] showed a good correlation between surgical outcome and removal of channels with high HFO rates. Rates[5,6,12], powers[5], and durations[6,12] of HFOs were higher within than outside the SOZ. Moreover, HFOs bursts mark epileptogenicity rather than lesion type[14]. In summary, HFOs bursts seem to be a reliable biomarker of epileptogenic tissue capable of producing seizures and can provide some useful information for understanding of the fundamental neural mechanisms underlying epileptic phenomena. Visual analysis of HFOs was previously provided a good and adequate understanding[5,6] of the relation of HFOs with epilepsy. However, this manual procedure is tedious especially for analyzing long and multi channels EEG recordings, time-consuming (it takes about 10 hour to visually mark HFOs in a 10- channel/10-min recording[15]), inevitably subjective. It is also possible that some actual small HFOs oscillations escape visual inspection[16]. Visual processing of HFOs may also be subject to error prone and requires a great deal of mental concentration and qualified/experienced reviewers. Thus, automated and reliable detection of HFOs may be more useful, fast, consistent, and objective than the visual identification. Moreover, automated software is crucial and necessary for the systematic study and investigation of HFOs in large scale research. A comparison of existing detectors on the same database is important to analyze their performance in terms of correct/false detection rate, and for comparing their robustness of detection. In the present framework, we firstly improved three existing HFOs detectors, which are based on time frequency techniques. We then compared their performance to that of a human reviewer using two commonly metrics: Sensitivity and False Discovery Rate (FDR). The first method is based on Complex MORLET Wavelet (CMV). The second is derived from Matching Pursuit (MP), and the third uses Bumps Modeling Technique (BMT). The structure of the paper parts is ordered as follows: Section.1 presents Introduction. Section.2 describes the clinical database. In section.3, the various details of the mentioned methods are provided. Section.4 describes visual marking of HFOs and section.5 presents performance metrics. Section.6 presents the discussion and the comparison of different methods. Last section presents conclusion and our outlines future work.
2. Clinical Database
- The clinical database used in the present study was recorded using the Harmonic system (Stellate) at the Montreal Neurological Institute and Hospital (MNI), Canada. The data was low-pass filtered at 500 Hz and subsequently sampled at 2000 Hz. Then, sampled data was quantized using a 16 bit analog-to-digital converter. In order to avoid the risk of focusing our study on a particular data, the used channels were chosen based on the following criteria: clear presence of interictal HFOs upon initial review is firstly controlled. Second, both channels with active and rare HFO events were considered. Third, a group of three consecutive patients with intractable epilepsy was considered for the current study. In the last, channels contain different background level were selected. All patients gave informed consent in agreement with the research ethics board of MNI.
3. Methods
- Time-frequency (TF) based methods are a combination of both theory and information. TF methods have been used extensively in the processing and analysis of non stationary signals, as found in a wide range of application including biomedical engineering. Their advantage can be resumed as follows: localization of information about both time and frequency together, automated classification of specific patterns based on their frequency components. They allow determining of coupling relationships among frequencies, amplitudes and phases of signals, which can provide insights about some underlying physiologic, pathologic process of many neurological diseases like Epilepsy, Parkinson and Alzheimer. TF based methods also allow measuring the reproducibility in signals and interpretation of models that may reflect pathological and physiological behavior in neuroscience.Details for HFOs detection using the mentioned methods are provided below:
3.1. Detection of HFOs based on Complex MORLET Wavelet (CMW Method)
- For HFOs detection based on CMW, power coefficients
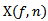 is firstly computed using the complex MORLET wavelet
is firstly computed using the complex MORLET wavelet 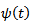 [2,17].
[2,17].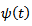 is defined as follows:
is defined as follows: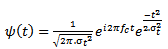 | (1) |
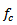 represents the central frequency of the mother wavelet
represents the central frequency of the mother wavelet 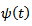 . The standard deviation
. The standard deviation 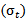 of the gaussian window used here is set to 1. The wavelet family is chosen so that the ratio of its center frequency to bandwidth is equal to 7, which corresponds to a good HFOs legibility and lead to the highest correlation coefficients with HFOs events. This choice according to the following equation:
of the gaussian window used here is set to 1. The wavelet family is chosen so that the ratio of its center frequency to bandwidth is equal to 7, which corresponds to a good HFOs legibility and lead to the highest correlation coefficients with HFOs events. This choice according to the following equation: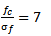 | (2) |
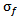 . The relationship between
. The relationship between 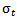 and
and 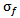 is defined as follows:
is defined as follows: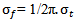 | (3) |
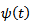 defined above in equation.1, can be scaled by a factor
defined above in equation.1, can be scaled by a factor 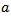 and translated by an amount b in time as follows:
and translated by an amount b in time as follows: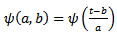 | (4) |
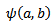 is known as a daughter wavelet. Scale
is known as a daughter wavelet. Scale 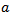 is related to a pseudo-frequency
is related to a pseudo-frequency 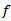 , according to the following relationship:
, according to the following relationship: 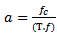 | (5) |
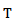 is the sampling period and
is the sampling period and 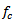 is equal to (7/2π) in our case. The wavelet power
is equal to (7/2π) in our case. The wavelet power 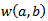 is then computed as follows:
is then computed as follows: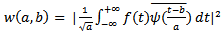 | (6) |
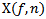 is computed from wavelet power
is computed from wavelet power 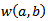 by transforming scale a into integer pseudo-frequency f using equation.5 and replacing b by the sample
by transforming scale a into integer pseudo-frequency f using equation.5 and replacing b by the sample 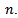 Pseudo frequency values ranging from 80Hz up to 500Hz with a step of 5Hz were used.
Pseudo frequency values ranging from 80Hz up to 500Hz with a step of 5Hz were used. 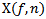 represents a three-dimensional map described in time (x-axis), pseudo-frequency (y-axis), and coefficient values (z-axis) in dB. Afterwards, to improve the localization of HFO events and to reduce noise impacts, time frequency map is subsequently smoothed using a robust smoothn function described in[18]. More details about this function are available at: http://www.biomecardio.com/matlab/smoothn.html.If an HFO is present, then it will create a local maximum (also called burst) in the power coefficients map
represents a three-dimensional map described in time (x-axis), pseudo-frequency (y-axis), and coefficient values (z-axis) in dB. Afterwards, to improve the localization of HFO events and to reduce noise impacts, time frequency map is subsequently smoothed using a robust smoothn function described in[18]. More details about this function are available at: http://www.biomecardio.com/matlab/smoothn.html.If an HFO is present, then it will create a local maximum (also called burst) in the power coefficients map 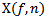 . For each burst exceeds a power threshold, the location of its maximum amplitude is determined, which automatically corresponds to a frequency
. For each burst exceeds a power threshold, the location of its maximum amplitude is determined, which automatically corresponds to a frequency 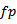 .For
.For 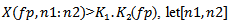 delimit the portion of the considered burst above the power threshold
delimit the portion of the considered burst above the power threshold 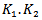
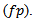 Where
Where 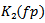 represents the corresponding power threshold which is a function of the pseudo frequency, and
represents the corresponding power threshold which is a function of the pseudo frequency, and 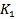 is a setting factor. Finally, If the temporal width
is a setting factor. Finally, If the temporal width 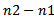 exceeds a duration
exceeds a duration 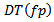 which is expressed in equation.7. Then, the temporal width
which is expressed in equation.7. Then, the temporal width 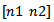 can be detected as a candidate HFO. The frequency
can be detected as a candidate HFO. The frequency 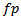 can characterize the detected HFO if a ripple or fast ripple.
can characterize the detected HFO if a ripple or fast ripple. 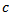 is the number of wave-cycles is fixed at 3,
is the number of wave-cycles is fixed at 3, 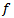 is the frequency of the detected burst, and
is the frequency of the detected burst, and 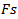 is the sampling frequency.
is the sampling frequency.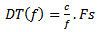 | (7) |
3.2. Detection of HFOs Based on Matching Pursuit (MP)
- The Matching Pursuit (MP) procedure[16,19,20, 21] relies on adaptive decomposition of the signal into weighted atoms. The atoms are drawn from a large redundant dictionary D. To implement our custom HFO detector, we used the implementation of the MP available at http://eeg.pl/mp. The dictionary D used in the mentioned software is constructed from a normalized real Gabor atom
 which can be expressed as follows:
which can be expressed as follows: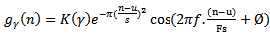 | (8) |
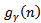 , that are respectively: the frequency
, that are respectively: the frequency 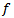 is used to quantify the frequency in (Hz) of the HFO burst. The time occurrence
is used to quantify the frequency in (Hz) of the HFO burst. The time occurrence 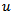 in (sample) is used to characterize the central timing of the HFO event. The scale
in (sample) is used to characterize the central timing of the HFO event. The scale 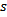 (in sample) approximates the duration of the HFO pattern. The phase
(in sample) approximates the duration of the HFO pattern. The phase  in (rad) corresponds to the phase of the HFO. Where
in (rad) corresponds to the phase of the HFO. Where 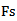 is the sampling frequency.
is the sampling frequency. 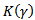 is chosen so that
is chosen so that 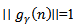 .At the ith iteration (i =1..... M), a best-match atom
.At the ith iteration (i =1..... M), a best-match atom 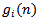 is selected from dictionary D, which maximizes the correlation with the residual
is selected from dictionary D, which maximizes the correlation with the residual 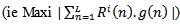 . Where
. Where 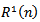 is the original signal and L its length. The procedure can be described by:
is the original signal and L its length. The procedure can be described by: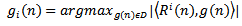 | (9) |
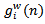 is derived from
is derived from 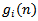 through the following equation:
through the following equation: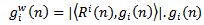 | (10) |
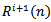 can be obtained by subtracting
can be obtained by subtracting 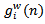 from the previous residual
from the previous residual 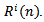
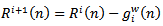 | (11) |
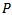 ).represents the energy percentage of the synthesized signal compared to the input original signal. The synthesized signal is the sum of the extracted weighted Gabor atoms
).represents the energy percentage of the synthesized signal compared to the input original signal. The synthesized signal is the sum of the extracted weighted Gabor atoms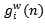 . Definition of the
. Definition of the 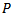 parameter is according to the following equation:
parameter is according to the following equation: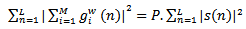 | (12) |
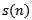 is the original signal.A given signal cannot be perfectly synthesized by few atoms. Too few atoms (low
is the original signal.A given signal cannot be perfectly synthesized by few atoms. Too few atoms (low 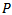 value) could miss some true oscillations have low amplitudes (for example a Fast Ripple pattern), while too many atoms (high
value) could miss some true oscillations have low amplitudes (for example a Fast Ripple pattern), while too many atoms (high 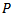 value) will end up in the last iterations as correction atoms (come from jumps, vertex waves, sharp waves, linearity…etc) which can be misclassified as true HFOs. In the fact, the main limitation for using parameter as an input setting for training our MP algorithm, that in last iterations when HFOs bursts have low amplitudes a
value) will end up in the last iterations as correction atoms (come from jumps, vertex waves, sharp waves, linearity…etc) which can be misclassified as true HFOs. In the fact, the main limitation for using parameter as an input setting for training our MP algorithm, that in last iterations when HFOs bursts have low amplitudes a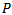 nd low energies are going to be extracted by MP decomposition, the noise can be modeled by lengthy Gabor atoms have low amplitudes and significant energies. Therefore, noise has the priority to be modeled as spurious HFOs events compared to numerous relevant HFOs have both low energies and amplitudes together. That could increase the false detection rate. Thus, P parameter should be diminished, which would also decrease the sensitivity. Another robust criterion was chosen for the detection of HFOs using MP, is to fit the signal in the first step with a high value of energetic parameter (P=99.99%), so that all relevant HFOs events can be extracted. Subsequently, a filtering MP in HFO band (80-500Hz) is applied. Each putative Gabor atom in the HFO band must satisfy the two following conditions to be as a candidate HFO: its amplitude (represents the input setting in the current study) must exceed a fixed threshold (its amplitude >
nd low energies are going to be extracted by MP decomposition, the noise can be modeled by lengthy Gabor atoms have low amplitudes and significant energies. Therefore, noise has the priority to be modeled as spurious HFOs events compared to numerous relevant HFOs have both low energies and amplitudes together. That could increase the false detection rate. Thus, P parameter should be diminished, which would also decrease the sensitivity. Another robust criterion was chosen for the detection of HFOs using MP, is to fit the signal in the first step with a high value of energetic parameter (P=99.99%), so that all relevant HFOs events can be extracted. Subsequently, a filtering MP in HFO band (80-500Hz) is applied. Each putative Gabor atom in the HFO band must satisfy the two following conditions to be as a candidate HFO: its amplitude (represents the input setting in the current study) must exceed a fixed threshold (its amplitude >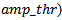 and its scale must also exceed a duration threshold which is equal to
and its scale must also exceed a duration threshold which is equal to 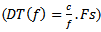 . Where f is the assessed frequency of the considered Gabor atom,
. Where f is the assessed frequency of the considered Gabor atom, 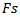 is the sampling frequency and c is the number of wave cycles is set to 3. Finally, as a final step, the grouping of overlapped detected Ripples and Fast Ripples into a single HFO event is done.
is the sampling frequency and c is the number of wave cycles is set to 3. Finally, as a final step, the grouping of overlapped detected Ripples and Fast Ripples into a single HFO event is done.3.3. Detection of HFOs Based on Bumps Modelling Thechnique (BMT)
- The bump modeling of a time-frequency map aims at representing the map with a set of predefined elementary parameterized functions called bumps[22]. The purpose of this technique was to reduce the huge quantity of parameters (hundreds of thousands coefficients) that describe a time-frequency map to a sum of parametric functions. A parsimonious representation is then obtained, which is relevant for further analysis, investigation and automated detection. The method is somewhat similar in spirit to the matching-pursuit algorithm that applied directly to the input original signal. In previous investigations, Bumps technique was successfully provides a quantitative estimate of the reproducibility of the time-frequency events[22]. Afterwards, it was used to investigate several aspects of brain oscillatory dynamics of Alzheimer's disease (AD)[22]. Bumps modeling technique was previously used for detection of HFOs bursts in[23]. Different details and improvement for detection of HFOs based on this method are described below:
3.3.1. Choice of Bump Function
- Different kinds of functions were used for bump modeling. The prominent function that was used in the processing of EEG signals and led to a smaller modeling error is the half-ellipsoid function which is defined as follows:
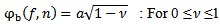
 | (13) |
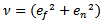
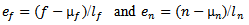 and
and 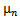 are the coordinates of the center of the half-ellipsoid function.
are the coordinates of the center of the half-ellipsoid function. 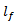 and
and 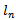 are the half-lengths of the principal axes along the frequency and time axes respectively, and
are the half-lengths of the principal axes along the frequency and time axes respectively, and 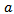 is its amplitude.
is its amplitude.3.3.2. Resolution and Windowing
- The time extension of wavelets is frequency-dependent: for high frequency, wavelets have a small time extension (high time resolution), but their frequency spectrum is large (low frequency resolution). Whereas, the inverse occurs at low frequency. The trade-off between the time resolution and frequency resolution is depending on Heisenberg-Gabor equation which is defined as follows:
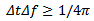 | (14) |
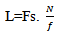 | (15) |
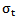 of a wavelet at that frequency is defined as:
of a wavelet at that frequency is defined as: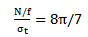 | (16) |
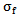 of the wavelet is also equal to 8π/7.
of the wavelet is also equal to 8π/7.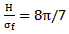 | (17) |
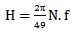 | (18) |
3.3.3. Define the Boundaries of the Map
- For each point of the map under consideration, a time-frequency window
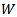 centered at that point is obtained. Due to boundaries effect in time-frequency map, the section of signal to be modeled must start with a fixed duration equal to (Fs.(N/2*fl)) before the useful part of the signal and stopped after it with the same duration. The lowest frequency must be started with frequency
centered at that point is obtained. Due to boundaries effect in time-frequency map, the section of signal to be modeled must start with a fixed duration equal to (Fs.(N/2*fl)) before the useful part of the signal and stopped after it with the same duration. The lowest frequency must be started with frequency 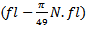 and the highest frequency must be stopped at
and the highest frequency must be stopped at 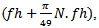 where
where  is set to 400 Hz and
is set to 400 Hz and 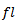 is set to 80 Hz.
is set to 80 Hz.3.3.4. Search for the Zone Containing the Maximal Amount of Oscillatory Activity
- The intensities map of the pixels contained in a window W describe the amount of oscillatory activity within the considered window. The modeling algorithm searches for the window Wmax containing the maximal energy amount: for each window W, the sum S of the intensities of the pixels within the window W is computed as follow:
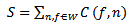 | (19) |
3.3.5. Bump Adaptation
- Within the selected window Wmax, a bump function
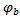 is adapted, starting with a bump extending over the whole area of the window. Thus, the bump function has five parameters, subject to the following constraints:-
is adapted, starting with a bump extending over the whole area of the window. Thus, the bump function has five parameters, subject to the following constraints:- 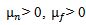 are represent the center of the bump lies within the window Wmax.-
are represent the center of the bump lies within the window Wmax.- 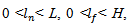 where L and H are the height and width of the window Wmax as defined by equation.15 and equation.18.- Amplitude a > 0.The adaptation phase is performed across the cost function E to be optimized based on the modeling error of the bump, defined by the sum of squared errors. The cost function is defined as follows:
where L and H are the height and width of the window Wmax as defined by equation.15 and equation.18.- Amplitude a > 0.The adaptation phase is performed across the cost function E to be optimized based on the modeling error of the bump, defined by the sum of squared errors. The cost function is defined as follows: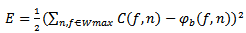 | (20) |
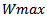 under consideration for instance.When the bump is finally adapted, it is subtracted from the original time-frequency map, and the process is iterated with the next bump. The procedure of bumps decomposition is done across Butlf toolbox[24,25] decomposition available at:http://www.bsp.brain.riken.jp/~fvialatte/bumptoolbox/toolbox_home.Thus, each modeled bump is restricted to one biologically HFO oscillation with duration of three periods. Longer oscillations will be modeled by two bumps or more (non-overlapping or overlapping).
under consideration for instance.When the bump is finally adapted, it is subtracted from the original time-frequency map, and the process is iterated with the next bump. The procedure of bumps decomposition is done across Butlf toolbox[24,25] decomposition available at:http://www.bsp.brain.riken.jp/~fvialatte/bumptoolbox/toolbox_home.Thus, each modeled bump is restricted to one biologically HFO oscillation with duration of three periods. Longer oscillations will be modeled by two bumps or more (non-overlapping or overlapping).3.3.6. Termination Criterion
- A trade-off usually exists between the rate of correct and false detection. If the number of bumps in the model is too low, the latter will not be sensitive; if it is too large, the noise will be modeled, hence irrelevant information would be built into the model, which could increase false detection rate. For the actual application, we first design a model with a largest number of bumps within a reasonable computation time (chosen header.limit parameter=0.0001[24,25]). Subsequently, each extracted bump must satisfy the following conditions to be as a candidate HFO: its frequency
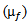 must be included in HFO band (80-400Hz), and its fraction ratio F is defined in equation.21 should exceed a threshold (Fc). Fc is considered as the input parameter for training the current method (if F>Fc, Bump is considered as a candidate HFO, else is rejected). The fraction ratio (F) of the intensity modeled by a one given bump to the total intensity of the map is computed as follows:
must be included in HFO band (80-400Hz), and its fraction ratio F is defined in equation.21 should exceed a threshold (Fc). Fc is considered as the input parameter for training the current method (if F>Fc, Bump is considered as a candidate HFO, else is rejected). The fraction ratio (F) of the intensity modeled by a one given bump to the total intensity of the map is computed as follows: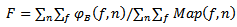 | (21) |
4. Visual Marking of HFOs
- Based on our custom Graphical User Interface (GUI), two reviewers trained in electrophysiology and HFOs analysis identified visually and independently all relevant HFOs included in the used channels. The visual marking of HFOs was performed by splitting the screen horizontally in which the reviewer can viewed a raw of unfiltered EEG and a filtered version (band-pass filtered at 80-500Hz) simultaneously. The unfiltered EEG signal is seen in the top plot and the filtered signal in the bottom plot. The filtered EEG is viewed at a higher gain than unfiltered EEG. The filter removes lower frequency components and helps to locate HFO events. The higher gain is necessary because HFOs have very low amplitudes compared to the unfiltered EEG signals. Each event is marked as a relevant HFO, if it seems as regular oscillation that has at least 3 consecutive periods, and can be clearly distinguished from the background activity in the filtered signal, and is confirmed in the unfiltered EEG signal. Each event detected by the two reviewers was considered as relevant HFO burst. The remaining events were excluded from the analysis. Finally, marked HFOs events were automatically saved in a database for future analysis.
5. Performance Metrics
- Performance measure was quantified using the False Discovery Rate (FDR) which is a robust metric that characterize the false detection rate. The sensitivity metric is used to quantify the rate of correct detection. The two metrics are defined as follows:
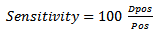 | (22) |
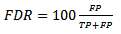 | (23) |
6. Result and Discussion
- Previous studies[5,6] proved that visual marking of HFOs provides a good understanding of some underlying brain mechanisms for epilepsy. However, this visual process is highly time consuming, subjective and might be subject to error-prone. Fast, objective, reliable and automated detection of HFOs is necessary for the systematic investigation of HFOs and to propel the clinical use of them as a reliable biomarker of epileptogenic tissue. Another important benefit of automated detection process: permits to parameterize the detected discharges such as determination of their position, duration, amplitude and frequency, estimation of HFOs rates, and assessment of HFOs power. These extracted parameters may be very useful for investigation of important clinical information like the determination of underlying dynamic change of HFOs during inter-ictal[5,6,10], pre-ictal and ictal[9] periods.Performance measure of HFOs detector depends on experts visual review- is considered the gold standard and must be associated with high inter-rater reliability. In the present study, 361 HFOs events were visually reviewed and considered as ground-truths for the performance measure and the comparison of the three improved existing HFOs detectors. The used data contains different background noise level, and includes both channels with active and rare HFOs rates. Receiver operating characteristic curves (ROC) of sensitivity vs. FDR, were used to test results of methods according to the different input parameters
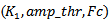 . The input parameters are respectively: the power threshold
. The input parameters are respectively: the power threshold 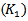 for CMOR wavelet based method, the amplitude threshold of Gabor atoms
for CMOR wavelet based method, the amplitude threshold of Gabor atoms 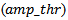 for MP method and the fraction ratio threshold
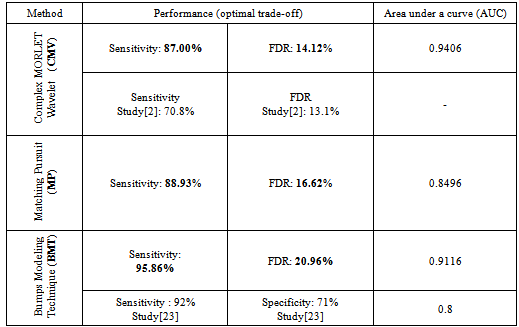
for MP method and the fraction ratio threshold 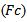 for Bumps method. During the training, the varying input parameter was considered optimal when the discrimination between undesirable (spurious HFOs) and desirable events (detected positives) was maximized as much as possible. That means the difference between the sensitivity and the FDR should be maximized. The choice of this criterion is clearly justified by Rahul et al[2].As is shown in figure.1, the optimal tradeoff between the sensitivity and the FDR for each method is indicated by the proper dash arrow for each curve. The table.1 illustrates a summarization of different results of the performance measure. The comparison is also done between our results and previous studies. Trapezoidal numerical integration method was used to determine the area under the ROC curves (AUC), the obtained AUC were respectively: 0.9406, 0.8496 and 0.9116.
for Bumps method. During the training, the varying input parameter was considered optimal when the discrimination between undesirable (spurious HFOs) and desirable events (detected positives) was maximized as much as possible. That means the difference between the sensitivity and the FDR should be maximized. The choice of this criterion is clearly justified by Rahul et al[2].As is shown in figure.1, the optimal tradeoff between the sensitivity and the FDR for each method is indicated by the proper dash arrow for each curve. The table.1 illustrates a summarization of different results of the performance measure. The comparison is also done between our results and previous studies. Trapezoidal numerical integration method was used to determine the area under the ROC curves (AUC), the obtained AUC were respectively: 0.9406, 0.8496 and 0.9116.
|
 | Figure 1. ROC curves of different methods: Optimal performance (best tradeoff) is indicated by the proper dash arrow for each curve |
 | Figure 2. A snapshot of HFOs detection using CMOR wavelet. Optimal configuration for the power threshold: K1=2.1 |
 | Figure 3. A snapshot of HFOs detection using Matching pursuit. Optimal configuration for the amplitude threshold of Gabor atoms: =5µv |
 | Figure 4. A snapshot of HFOs detection using Bumps modeling technique. Optimal configuration for the Fraction ratio threshold is set to: Fc =0.00003 |
7. Conclusions and Perspectives
- An automated and reliable detector is crucial for the investigation of HFOs and for the understanding of their relationship to the underlying pathology in epilepsy.Thus, several automatic detectors were developed for different EEG recordings and with different aims. Improving and comparing them in a single dataset is important to analyze their performance and robustness. The efficiency of the tested methods described in the current study depends on the required sensitivity and the FDR, which are related to the intended application (supervised or unsupervised detection method, time computation, complexity,…).As a conclusion, the three algorithms described here can achieve a high sensitivity. Bumps modeling based method can achieve a high sensitivity up to 98% with the minimum FDR compared to MP and CMOR wavelet based methods. To date, there can be an overlap between the time–frequency representation of transients (spikes, sharp waves, artifacts) and HFOs oscillations. The majority of HFOs detection methods are frequency based decomposition that can lead easily to detection of false-positive events, which arise essentially from the filtering of spikes and sharp waves without HFOs. Still, the best method must have as much sensitivity as possible to correctly detect all true HFOs events included in EEG data. False detection should be reduced to the minimum as possible. Also the best method should not be sensitive to spikes/ sharp waves without HFOs. In addition, such a robust detector should perform in a similar way for all types of channels with active and rare events and for different background levels. Further studies based on advanced signals processing are needed, such as the approaches based on mathematical morphology and geometric analysis, which may discriminate between transients without HFOs and transients with HFOs. This can improve the detection performance of different algorithms in large scale. Another potential interesting path that could be further explored is to address the question of whether a consensus automatic procedure that combines all three available methods (e.g. letting each method vote on each event) could outperform the results of a single approach. This can also improve our results and reduce false detection rate. Still, fast software and powerful systems are needed. Our future work will be focused on analyzing large amounts of EEG data using scalp EEG recordings and Invasive EEG based on a consensus automatic procedure that combines all the three available methods.
ACKNOWLEDGEMENTS
- Authors wish to thank the Montreal Neurological Institute and Hospital (MNI, Canada) for kindly providing database which we used to test and compare the performance of current methods. We would like to thank Dr. Mohamed Dogui (Service of Functional Exploration of the Nervous System, CHU Sahloul of Sousse, Tunisia) for helping us doing visual identification process of high frequency oscillations in EEG.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML