Aksenov I. B.
Kazan National Research Technical University A.N.Tupolev Kazan, 42011, Russia
Correspondence to: Aksenov I. B. , Kazan National Research Technical University A.N.Tupolev Kazan, 42011, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The mathematical model of excitement of oscillator with dissipation of energy of general form is considered. The received analytical expression in an explicit form describes changes of amplitude and the phases of a signal brought by an exciting signal. The signal of excitement of oscillator is modulated by periodic sequence of rectangular impulses and restriction of square-law integratability is imposed on it. Finite-difference approximation of the offered model by a method of state variables is constructed and the method of generation of chaotic sequences with fractal properties created on its basis. Results of numerical modelling of chaotic sequences with fractional value of the fractal dimensionality calculated by a method of correlative integral are given. The type of the attractors constructed on the basis of finite-difference approximation of received model is given, and it is shown that by change of parameters of model there is possible to receive chaotic sequences with fractal properties.
Keywords:
Oscillatory System, Chaotic Sequences, Fractal Properties
Cite this paper:
Aksenov I. B. , "Model of Excitation of Chaotic Fluctuations in Oscillatory system with dissipation", American Journal of Signal Processing, Vol. 2 No. 5, 2012, pp. 150-153. doi: 10.5923/j.ajsp.20120205.09.
1. Introduction
The oscillator is collective concept of the device, where under the influence of external perturbing influences possibly appear oscillatory processes. Examples of oscillators in mechanical system are the pendulum and oscillating dampening slug, in electrical system is a circuit from sequentially switched on elements: inductance, condenser and resistance, LCR a circuit.The works devoted to the analysis of origin of chaotic oscillations in a rotator with parametric excitation by periodic sequence of infinite and short pulses [1, 2] are known.Model chaotic processes with fractal properties find application in development of communications mediums, coding, compression of signals and they are generated on the basis of different approaches. In operations [3,5] by authors are considered oscillators with the chaotic modes, containing model, physically implementable, including non-linear elements . In [6-9] numerical methods and algorithms of generation of chaotic sequences on the basis of differential equations and Wavelet - expansions are offered.In [10-11] the approach based on simulation of modified chaotic attractors is developed. Modes of chaotic synchronization are considered.In this article the mathematical model of the oscillator excited by a signal of general form restricted by square integratability is considered. The model is received on the basis of Fourier integral and underlies generation of chaotic sequences. The suggested model is different from other by the mode of chaotic oscillations, that is realized in line circuit being excited by consequence of periodic rectangular pulses.
2. Basic Equations
Let's consider forced oscillations in oscillator excited by a signal 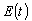 , having spectrum Fourier
, having spectrum Fourier 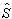 modulated by periodic sequence of rectangular impulses. Then
modulated by periodic sequence of rectangular impulses. Then 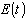 it is possible to write down as return transformation Fourier:
it is possible to write down as return transformation Fourier: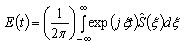 | (1) |
Thus generally the mode of excitation can have a periodic character and a spectrum of the entrance signal submitted on oscillatory system will become: 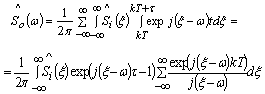 | (2) |
Where is respectively the period of time and duration of sequence of the rectangular impulses. Further identical conversion (2) is executed by changeover of variables with identical ratios of generalized functions theory: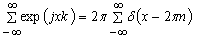 | (3) |
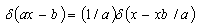 | (4) |
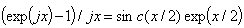 | (5) |
Where in (3,4,5) 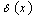 - Dirac delta function, and
- Dirac delta function, and 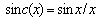 After performance of convolution with delta - function (2) will be as follows:
After performance of convolution with delta - function (2) will be as follows: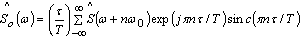 | (6) |
Where 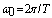 - is a frequency of sequence of rectangular impulses. The result (6) is received without the prior restrictions imposed by the theorem of Nyquist–Shannon when
- is a frequency of sequence of rectangular impulses. The result (6) is received without the prior restrictions imposed by the theorem of Nyquist–Shannon when 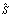 and
and 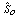 are the continuous values.Expression (6) in an obvious kind shows the changes of the module and argument of a range of the signal, entered by modulating rectangular sequence and existence in it the incremental frequencies such as:
are the continuous values.Expression (6) in an obvious kind shows the changes of the module and argument of a range of the signal, entered by modulating rectangular sequence and existence in it the incremental frequencies such as: 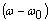 .Despite periodicity of modulating sequence expression (6) generally is not a periodic function. Let's consider a special case when the sequence of square pulses moves on serial oscillatory - a
.Despite periodicity of modulating sequence expression (6) generally is not a periodic function. Let's consider a special case when the sequence of square pulses moves on serial oscillatory - a 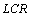 circuit being one of varieties of oscillator.Temporal dependence of a current in
circuit being one of varieties of oscillator.Temporal dependence of a current in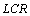 - circuits takes the form of Fourier theorem (6) in transmitting function - a circuit looks like:
- circuits takes the form of Fourier theorem (6) in transmitting function - a circuit looks like: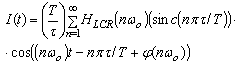 | (7) |
where: 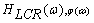 is accordingly the module and argument of transmission ratio of an oscillating circuit.Depending on specific implementation of oscillator value (7) may have different physical sense. When the oscillator represents the fluctuating dampening slug, (7) is speed of its mechanical oscillations arising under the influence of rectangular impulses of influencing force. Generally expression (7) is neither periodic, nor quasiperiodic function of time since change of arguments of all its multiplicands for the period doesn't return its value.If impose on phase shift of harmonicas of exciting frequency a look condition: that for specific values it is equivalent to a synchronization condition, i.e. in case of its execution the output signal acquires quasiperiodic character.
is accordingly the module and argument of transmission ratio of an oscillating circuit.Depending on specific implementation of oscillator value (7) may have different physical sense. When the oscillator represents the fluctuating dampening slug, (7) is speed of its mechanical oscillations arising under the influence of rectangular impulses of influencing force. Generally expression (7) is neither periodic, nor quasiperiodic function of time since change of arguments of all its multiplicands for the period doesn't return its value.If impose on phase shift of harmonicas of exciting frequency a look condition: that for specific values it is equivalent to a synchronization condition, i.e. in case of its execution the output signal acquires quasiperiodic character.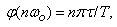 | (8) |
In particular case, when the frequency operator is transmission function 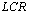 - circuits, a condition (8) takes a form:
- circuits, a condition (8) takes a form: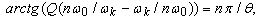 | (9) |
where: 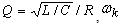 - respectively good quality and resonance frequency of an oscillating circuit;
- respectively good quality and resonance frequency of an oscillating circuit; 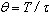 is on-off time ratio of pulses of excitation .The analysis of formulas (7) - (9) allows to find the mechanism of formation of chaotic oscillations. In a case when resonance frequency of oscillator isn't multiple to frequencies of the harmonics of parametric excitation, the irregular components will be formed by a compound of harmonicas of the exciting frequency modulated by the frequency operator of a source of a signal and the frequency operator of oscillator.Thus oscillation phase of these harmonics also appears depending on the phase-frequency characteristics, both a signal source, and oscillator.From the mathematical point of view the given expression is an example of converging in the mean functional row meeting on the average in which fluctuations of convergence are shown in the form of the small, determined chaos.
is on-off time ratio of pulses of excitation .The analysis of formulas (7) - (9) allows to find the mechanism of formation of chaotic oscillations. In a case when resonance frequency of oscillator isn't multiple to frequencies of the harmonics of parametric excitation, the irregular components will be formed by a compound of harmonicas of the exciting frequency modulated by the frequency operator of a source of a signal and the frequency operator of oscillator.Thus oscillation phase of these harmonics also appears depending on the phase-frequency characteristics, both a signal source, and oscillator.From the mathematical point of view the given expression is an example of converging in the mean functional row meeting on the average in which fluctuations of convergence are shown in the form of the small, determined chaos.
3. Discrete Model
The discrete LCR-model of the vibrating system excited by periodic sequence of square pulses in a time domain is received by a method of state variables[14], on the basis of a differential equation: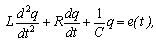 | (10) |
where q- the charge; e(t)- the exciting voltageThe first derivative of a charge corresponds to value of the circuit current, the second derivative to the speed of change of a current.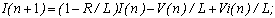 | (11) |
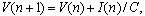 | (12) |
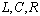 - values of inductance, capacitor capacities and resistance;
- values of inductance, capacitor capacities and resistance;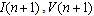 are respectively values of a current in inductance and tension on the condenser in
are respectively values of a current in inductance and tension on the condenser in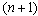 the discrete counting of time;
the discrete counting of time; 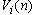 tension of a source of a signal in (n) time counting.
tension of a source of a signal in (n) time counting.
4. Numerical Modelling
Figure 1. reffers to the result of numerical modelling (11),(12). Thus the current component which can be observed directly on the resistor has the chaotic appearance reminding chaos through an separation[1, 15 ].When numerical modelling natural frequency - vibrating system and frequency of following pulses were selected not multiple, duration of pulses of excitation 0.2. 0.4 of frequency period of excitation. It is necessary to mention that when scaling time slots being watched oscillations show self-similarity elements.Numerical modelling of system of the equations (11-12) for LCR oscillatory system, raised by periodic sequence of rectangular pulses with parameters Q=10 and θ=13/50.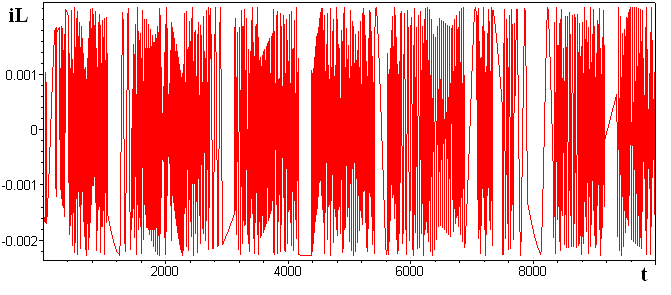 | Figure 1. The diagram of dependence of current in circuit on time |
Figure 2. refers to the central part of the attractor LCR-of vibrating system in the phase space, as dependence of the current proceeding in a circuit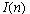 on tension on the condenser
on tension on the condenser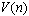 .The given attractor of LCR oscillator is the attractor of chaotic type and possesses Hausdorff-Besicovitch dimension equal to 1.6.Figure 3. refers to the histogram of value distribution of a current
.The given attractor of LCR oscillator is the attractor of chaotic type and possesses Hausdorff-Besicovitch dimension equal to 1.6.Figure 3. refers to the histogram of value distribution of a current 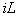 after completion of transient process.
after completion of transient process.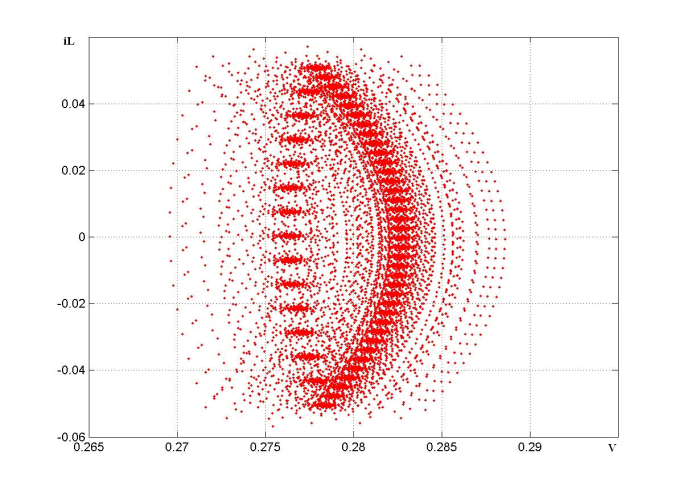 | Figure 2. The chaotic attractor LCR - vibrating system |
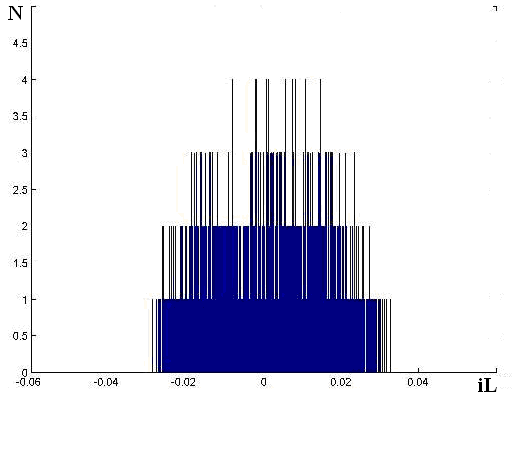 | Figure 3. Histogram of value distribution of a current iL |
On Figure 4 the attractor with fractal dimensionality ≈1.87 for LCR vibrating system with parameters L = 10, С=10,Q = 9, θ =50/3 is shown. On Figure 5 almost cyclical attractor with fractal dimensionality ≈ 1.74 for L, C, R vibrating system with parameters L = 10, С=10,Q = 9, θ =50/13 is shown.It is necessary to notice the system of equations (11-12) which decisions generally have chaotic character and allow to implement different histograms of distribution of amplitude of a current of a LCR- circuit isn't steady. The problem of stability of the decision is required to be decided in each case separately.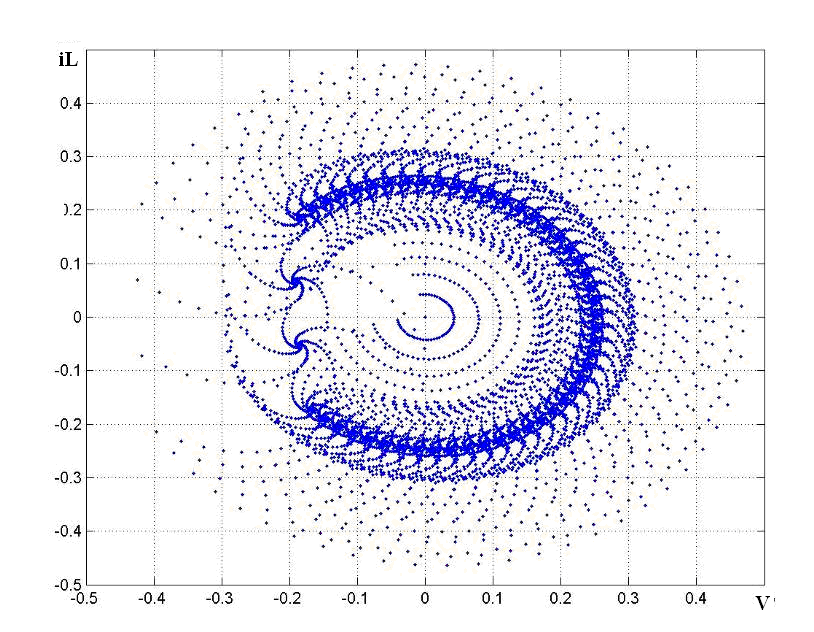 | Figure 4. The attractor - vibrating system |
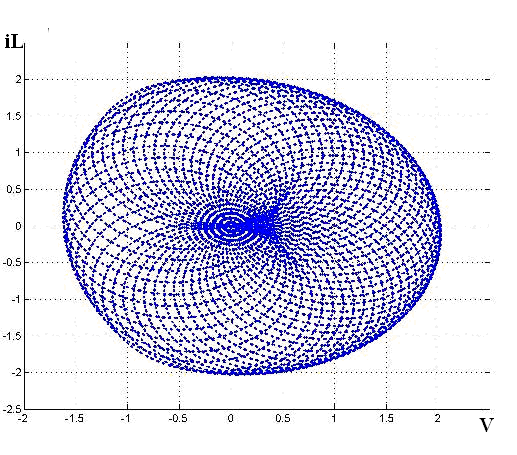 | Figure 5. The attractor LCR - vibrating system, H ≈ 1.74 |
Combination of values of elements of vibrating system and choice of values of the period and duration of input sequence it is possible to receive attractors of a chaotic view, with fractal dimensionality as it is more, and less than 1. The considerable influence on value of fractal dimensionality is rendered by on-off time ratio of impulse sequence and value of good quality.
5. Conclusions
The method of integral Fourier receives mathematical model of excitation of fluctuations in oscillatory system with dissipation a signal having square integratability, modulated by sequence of rectangular pulses. The condition of occurrence chaotic a mode of oscillations is formalized and numerical modelling of fluctuations in linear LCR- oscillatory system is performed on a basis of differential equations. The opportunity to generate chaotic sequences with values of Hausdorf dimensionality that are more than 1 and less than 1 is shown. Results of modelling of the fluctuations, received on electric model LCR- oscillatory system are generalized for other physical systems.
ACKNOWLEDGEMENTS
The author is gratitude to his daughter, Eugenia Kirillina, who performed the translation into the English language.
References
| [1] | Schuster H.G. Deterministic Chaos. An Introduction, Wiley-VCH, 2004. |
| [2] | Zaslavsky, G. M. The Simplest Case of a Strange Attractor, Phys. Lett. 69 A (3) , 1978. |
| [3] | H. Muller. Fractal Scaling Models of Resonant Oscillations in Chain Systems of Harmonic Oscillators. PROGRESS IN PHYSICS. Vol.2, pp. 72-76, 2009. |
| [4] | W. Marszalek, Circuits with oscillatory hierarchical Farey sequences and fractal properties, Circuits, Systems, Signal Processing, 2012, (DOI) 10.1007/ s00034-012-9392-3. |
| [5] | A. Prasad. Universal occurrence of mixed-synchronization in counter-rotating nonlinear coupled oscillators Chaos Solitons & Fractals - CHAOS SOLITON FRACTAL vol. 43, no. 1, pp. 42-46, 2010 |
| [6] | Bolotov V.N., Tkach Yu.V. Generation of Fractal Spectrum Signals, Technical Physics, 2006, v 76, ed.4, p.91-98M. |
| [7] | V. F. Dailyudenko. Localized Approaches for Nonlinear Analysis of Chaotic Systems in Multidimensional Phase Space. The Open Cybernetics and Systemics Journal, 2009, 3, 40-46 |
| [8] | Pasic and S. Tanaka, Fractal oscillations of self-adjoint and damped linear differential equations of second-order, Applied Mathematics and Computation, 2011, pp.2281-2293. |
| [9] | M. Pasic and S. Tanaka, Fractal oscillations of self-adjoint and damped linear differential equations of second-order, Applied Mathematics and Computation, 2011, pp.2281-2293. |
| [10] | Pehlivan .., Uyaroglu Y., Simplified Chaotic Diffusionless Lorenz Attractor and its Application to Secure Communication Systems, IET Communications, 1(5), 1015-1022, 2007. |
| [11] | Pehlivan .., Uyaroglu Y., A New Chaotic attractor from General Lorenz System Family and its Electronic Experimental Implementation, Turkish Journal of Electrical Eng. Comput. Sci. 18(2), 171-184, 2010. |
| [12] | Pehlivan .., Uyaroglu Y., Yogun M., “Chaotic Oscillator Design andс Realizations of the Rucklidge Attractor and its Synchronization and Masking Simulations”, Scientific Research and Essays, Vol. 5(16), pp. 2210-2219, 2010. |
| [13] | Pehlivan .., UyarogluY., Rikitake Attractor and its Synchronization Application for Secure Communication Systems, Journal of Applied Sciences, 7(2):232-236, 2007. |
| [14] | Sibert U.M. Circuits and Systems II. p.1: Massachusetts Institute of Technology, 1986. |
| [15] | Aksenov I.B. Express diagnostics of dynamic processes. Methods of creation of hardware. Publishing house of Kazan National Research Technical University, 2004 |

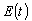 , having spectrum Fourier
, having spectrum Fourier 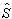 modulated by periodic sequence of rectangular impulses. Then
modulated by periodic sequence of rectangular impulses. Then 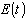 it is possible to write down as return transformation Fourier:
it is possible to write down as return transformation Fourier: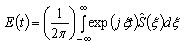
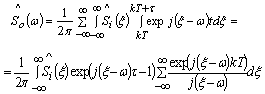
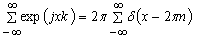
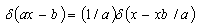
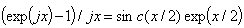
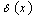 - Dirac delta function, and
- Dirac delta function, and 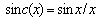 After performance of convolution with delta - function (2) will be as follows:
After performance of convolution with delta - function (2) will be as follows: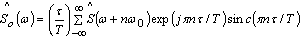
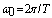 - is a frequency of sequence of rectangular impulses. The result (6) is received without the prior restrictions imposed by the theorem of Nyquist–Shannon when
- is a frequency of sequence of rectangular impulses. The result (6) is received without the prior restrictions imposed by the theorem of Nyquist–Shannon when 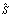 and
and 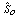 are the continuous values.Expression (6) in an obvious kind shows the changes of the module and argument of a range of the signal, entered by modulating rectangular sequence and existence in it the incremental frequencies such as:
are the continuous values.Expression (6) in an obvious kind shows the changes of the module and argument of a range of the signal, entered by modulating rectangular sequence and existence in it the incremental frequencies such as: 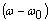 .Despite periodicity of modulating sequence expression (6) generally is not a periodic function. Let's consider a special case when the sequence of square pulses moves on serial oscillatory - a
.Despite periodicity of modulating sequence expression (6) generally is not a periodic function. Let's consider a special case when the sequence of square pulses moves on serial oscillatory - a 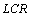 circuit being one of varieties of oscillator.Temporal dependence of a current in
circuit being one of varieties of oscillator.Temporal dependence of a current in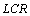 - circuits takes the form of Fourier theorem (6) in transmitting function - a circuit looks like:
- circuits takes the form of Fourier theorem (6) in transmitting function - a circuit looks like: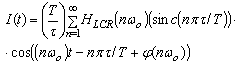
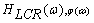 is accordingly the module and argument of transmission ratio of an oscillating circuit.Depending on specific implementation of oscillator value (7) may have different physical sense. When the oscillator represents the fluctuating dampening slug, (7) is speed of its mechanical oscillations arising under the influence of rectangular impulses of influencing force. Generally expression (7) is neither periodic, nor quasiperiodic function of time since change of arguments of all its multiplicands for the period doesn't return its value.If impose on phase shift of harmonicas of exciting frequency a look condition: that for specific values it is equivalent to a synchronization condition, i.e. in case of its execution the output signal acquires quasiperiodic character.
is accordingly the module and argument of transmission ratio of an oscillating circuit.Depending on specific implementation of oscillator value (7) may have different physical sense. When the oscillator represents the fluctuating dampening slug, (7) is speed of its mechanical oscillations arising under the influence of rectangular impulses of influencing force. Generally expression (7) is neither periodic, nor quasiperiodic function of time since change of arguments of all its multiplicands for the period doesn't return its value.If impose on phase shift of harmonicas of exciting frequency a look condition: that for specific values it is equivalent to a synchronization condition, i.e. in case of its execution the output signal acquires quasiperiodic character.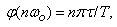
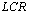 - circuits, a condition (8) takes a form:
- circuits, a condition (8) takes a form: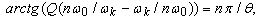
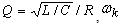 - respectively good quality and resonance frequency of an oscillating circuit;
- respectively good quality and resonance frequency of an oscillating circuit; 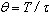 is on-off time ratio of pulses of excitation .The analysis of formulas (7) - (9) allows to find the mechanism of formation of chaotic oscillations. In a case when resonance frequency of oscillator isn't multiple to frequencies of the harmonics of parametric excitation, the irregular components will be formed by a compound of harmonicas of the exciting frequency modulated by the frequency operator of a source of a signal and the frequency operator of oscillator.Thus oscillation phase of these harmonics also appears depending on the phase-frequency characteristics, both a signal source, and oscillator.From the mathematical point of view the given expression is an example of converging in the mean functional row meeting on the average in which fluctuations of convergence are shown in the form of the small, determined chaos.
is on-off time ratio of pulses of excitation .The analysis of formulas (7) - (9) allows to find the mechanism of formation of chaotic oscillations. In a case when resonance frequency of oscillator isn't multiple to frequencies of the harmonics of parametric excitation, the irregular components will be formed by a compound of harmonicas of the exciting frequency modulated by the frequency operator of a source of a signal and the frequency operator of oscillator.Thus oscillation phase of these harmonics also appears depending on the phase-frequency characteristics, both a signal source, and oscillator.From the mathematical point of view the given expression is an example of converging in the mean functional row meeting on the average in which fluctuations of convergence are shown in the form of the small, determined chaos.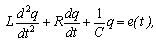
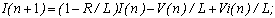
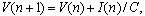
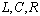 - values of inductance, capacitor capacities and resistance;
- values of inductance, capacitor capacities and resistance; are respectively values of a current in inductance and tension on the condenser in
are respectively values of a current in inductance and tension on the condenser in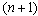 the discrete counting of time;
the discrete counting of time; 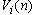 tension of a source of a signal in (n) time counting.
tension of a source of a signal in (n) time counting.
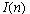 on tension on the condenser
on tension on the condenser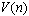 .The given attractor of LCR oscillator is the attractor of chaotic type and possesses Hausdorff-Besicovitch dimension equal to 1.6.Figure 3. refers to the histogram of value distribution of a current
.The given attractor of LCR oscillator is the attractor of chaotic type and possesses Hausdorff-Besicovitch dimension equal to 1.6.Figure 3. refers to the histogram of value distribution of a current 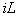 after completion of transient process.
after completion of transient process.



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML