Rajesh Ku. Tripathy 1, Ashutosh Acharya 2, Sumit Kumar Choudhary 2
1Department of Bio Medical Engineering, NIT, Rourkela, India
2Department of Electronics and Comm. Engineering, SIT, Bhubaneswar, India
Correspondence to: Rajesh Ku. Tripathy , Department of Bio Medical Engineering, NIT, Rourkela, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this present paper it deals with the Gender Classification from ECG signal using Least Square Support Vector Machine (LS-SVM) and Support Vector Machine (SVM) Techniques. The different features extracted from ECG signal using Heart Rate Variability (HRV) analysis are the input to the LS-SVM and SVM classifier and at the output the classifier, classifies whether the patient corresponding to required ECG is male or female. The least square formulation of support vector machine (SVM) has been derived from statistical learning theory. SVM has already been marked as a novel development by learning from examples based on polynomial function, neural networks, radial basis function, splines and other functions. The performance of each classifier is decided by classification rate (CR). Our result confirms the classification ability of LS-SVM technique is much better to classify gender from ECG signal analysis in terms of classification rate than SVM.
Keywords:
ECG, HRV, SVM, LS-SVM, CR
Cite this paper:
Rajesh Ku. Tripathy , Ashutosh Acharya , Sumit Kumar Choudhary , "Gender Classification from ECG Signal Analysis using Least Square Support Vector Machine", American Journal of Signal Processing, Vol. 2 No. 5, 2012, pp. 145-149. doi: 10.5923/j.ajsp.20120205.08.
1. Introduction
Gender is almost its most salient feature, and gender classification according to ECG is one of the most Challenging problems in person identification in Biometrics[1]. Compared with other research topics in Biometrics, the academic researches on gender classification is less. In reality, successful gender classification will boost the performance of Patient recognition in large Medical database. From last two decades It was observed that a variety of prediction models have been proposed in the machine learning that include time series models, regression models, adaptive neuro-fuzzy inference systems (ANFIS), artificial neural network (ANN) models and SVM models[2]. Due to the effectiveness and smoothness of ANN model, it is widely used in various fields like pattern recognition, regression and classification. For classification and non-linear function estimation, the recently proposed SVM technique is an innovative kind of machine learning method introduced by Vapnik and co-workers[3, 4, 5]. This method is further enhanced by various investigators for different applications like classification, feature extraction, clustering, data reduction and regression in different disciplines. SVM have remarkable generalization performance and many more advantages over other methods, and hence SVM has attracted attention and gained extensive application. Suykens and his group[6] have proposed the use of LS-SVM for simplification of traditional of SVM. Apart from its use in classification in various areas of pattern recognition, it has been extensively used in handling regression problems successfully[7, 8]. In LS-SVM, a set of only linear equation (Linear programming) is solved which is much easier and computationally more simple which made it advantageous than SVM. In the present study, both SVM and LS-SVM classifiers have been designed, trained and tested using various kernel functions like linear and (Radial Basic Function) RBF kernel. RBF kernel LS-SVM gives better performance in terms of classification rate among other classifiers.
2. Materials and Methods
In this current study, the ECG of different people was recorded. An in-house developed ECG data acquisition system was used for this study. The ECG system mainly composed of two parts, viz. ECG electrodes and ECG-DAQ. ECG-DAQ, a USB-based device, helped in recording ECG signals in PC. Figure 1 shows the ECG device connected with PC which was used for data recording in our study.Biomedical Starter Kit from National Instrument software was used to extract the different time and frequency domain features of HRV (e.g. mean heart rate (HR), mean RR, Mean NN, standard deviation of RR intervals (SDNN), root mean square of successive difference (RMSSD), NN50, pNN50 and SD1 and SD2 of Poincare plot). The HRV features were then analysed by non-linear statistical analysis using Classification and regression trees (CART) and Boosted tree (BT) classification to determine the significant features in STATISTICA (v7) in figure 2. A combination of the features was subsequently used for Gender Classification using SVM and LS-SVM in MATLAB 10.1. After prediction of significant features like(RR Mean, RR Standard Deviation(std.),HR mean, HR Std, root mean square of successive difference (RMSSD), NN50, pNN50,LF peak, HF Peak, LF Power, HF Power, LF/HF ratio) from CART and BT then these feature values are the input to both SVM classifier. At the output of both classifiers we will classify two classes i.e. (boy and girl).the binary values assigns to girl class as 0 and for boy class the value is 1.After classification we compare both the values in terms of Classification rate (CR). | Figure 1. Custom made ECG device |
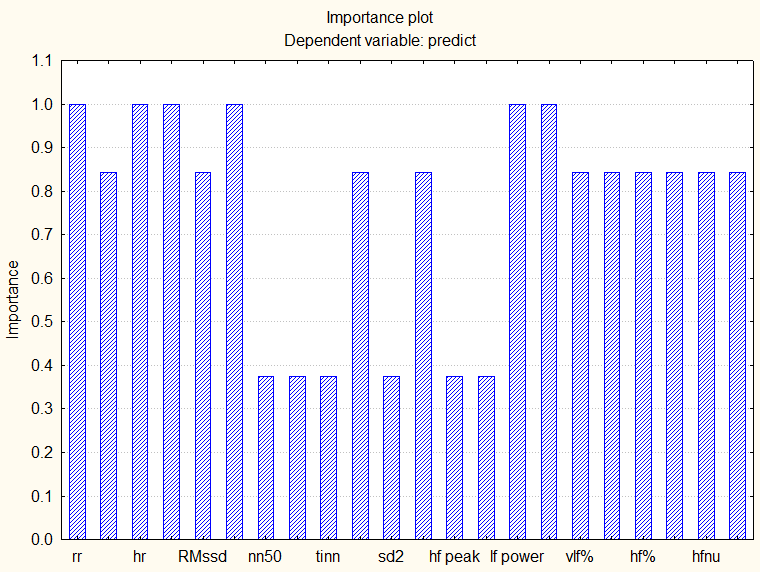 | Figure 2. Significant Input parameters for gender classification |
The input data are normalized before being processed in the network as follows:In this method of normalization, the maximum values of the input vector component are given by: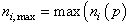 , p=1 …Np, i= 1….NiWhere ni(p) is the input features and Np is the number of patterns in the training set and testing set,
, p=1 …Np, i= 1….NiWhere ni(p) is the input features and Np is the number of patterns in the training set and testing set,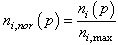 , p = 1….Np , i = 1,…NiAfter normalization, the input variables lie in the range of 0 to 1.
, p = 1….Np , i = 1,…NiAfter normalization, the input variables lie in the range of 0 to 1.
3. SVM Classification
SVM technique is an attractive kind of machine learning method introduced by Vapnik and co-workers[3, 4, 5]. This method is further modified by various scientists for different applications like classification, feature extraction, clustering, data reduction and regression in different disciplines of engineering. Our present analysis is based on the classification of binary class data by employing SVM technique. This method builds a Hyperplane for separation of data into two classes in simple binary classification of linear separable training data vector ( ) in n dimensional Space. A class decision function associated with Hyperplane is weighted sum of training data set and bias are symbolized[10, 11, 12] as
) in n dimensional Space. A class decision function associated with Hyperplane is weighted sum of training data set and bias are symbolized[10, 11, 12] as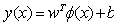 | (3.1) |
Where ‘w’ and ‘b’ are weight vector normal to Hyperplane and bias value respectively. New test data according to the classification by SVM classifier is assigned to a class according to sign of decision function as:Testing data belongs to class-1(male class) if 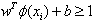 | (3.2) |
Test data belongs to class-2(female class) if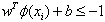 | (3.3) |
And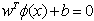 | (3.4) |
Is the decision boundary corresponding to Weight vector and bias value for optimal Hyperplane. Support vectors are obtained by maximizing the distance between the closest training point and the corresponding Hyperplane. This can be done by maximizing the margin defined as 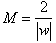 same as minimization of
same as minimization of 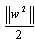 | (3.5) |
Under the methodologies 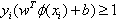 | (3.6) |
Different number of mathematical algorithms exists for determining the value of weight and bias under the condition (3.5) and (3.6). One of the most efficient method used in SVM is Quadratic Optimization problem. Its solution of the problem involves construction of dual problem with the use of Lagrange multiplier 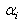 which is given as follows:
which is given as follows: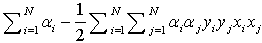 | (3.7) |
The equation (3.7) is maximized under the conditions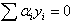 and
and 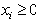 For all value of
For all value of 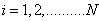 .After solving Quadratic optimization problem, the values of weight and bias are obtained as
.After solving Quadratic optimization problem, the values of weight and bias are obtained as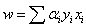 | (3.8) |
And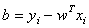 | (3.9) |
Where 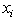 is support vector for each nonzero value of
is support vector for each nonzero value of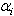 . Hence, the classification function for a test data point
. Hence, the classification function for a test data point 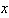 is inner product of support vector and test data point, which is given as follows
is inner product of support vector and test data point, which is given as follows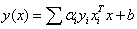 | (3.10) |
SVM maps n-dimensional data vector into a d-dimensional feature space (d>n) with help of a mapping function for binary classification of nonlinear training data points. This Mapping function or kernel function provides a Hyperplane which separate the classes in high dimensional feature space. Using standard Quadratic Programming (QP) optimization technique, the Hyperplane maximizes the margin between classes. Those data point which are Closest to the Hyperplane are used to measure the margin and named as support vectors. In dual formulation of quadratic optimization problem instead of using dot product of training data points in high dimensional feature space, kernel trick is used. Kernel function defines the inner product of training data points in high dimensional feature space.Thus the kernel function is defined as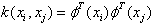 | (3.11) |
The various advantages of kernel function are, It reduces the mathematical as well as the computational complexity in higher dimensional feature space. In this paper, commonly used kernel functions are linear, polynomial, radial Gaussian and sigmoid are defined as follows: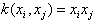 (Linear kernel Function)
(Linear kernel Function)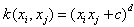 For
For 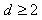 and
and 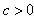 (Polynomial Kernel Function)
(Polynomial Kernel Function)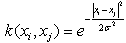 For
For 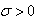 (Radial Gaussian kernel function)The new classification function using kernel function is defined as follows:
(Radial Gaussian kernel function)The new classification function using kernel function is defined as follows: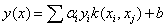 | (3.12) |
Further, the testing data points are classified with these binary class trained model and final decision about class of data point is taken on the basis of majority voting of class. The performance of model is determined by classification rate equal to 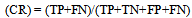 | (3.13) |
Where TP=True Positive, TN=True Negative, FP=False Positive and FN=False Negative.
4. LS-SVM Classification
The formulation of LS-SVM is introduced as follows. Given a training set 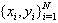 with input data
with input data 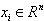 and corresponding binary class labels
and corresponding binary class labels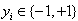 .The following Classification model can be constructed by using non-linear mapping function
.The following Classification model can be constructed by using non-linear mapping function 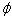 (x)[11].
(x)[11].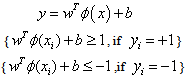 | (4.1) |
Where w weight is vector and b is the bias term[9,10, 11]. As in LS-SVM, it is necessary to minimize a cost function C containing a penalized regression error for binary target, as follows: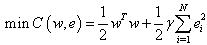 | (4.2) |
Subject to equality constraints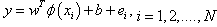 | (4.3) |
The first part of this cost function is a weight decay which is used to regularize weight sizes and penalize large weights. Due to this regularization, the weights converge to similar value. Large weights deteriorate the generalization ability of the LS-SVM because they can cause excessive variance. The second part of eq. (4.2) is the regression error for all training data. The parameter y, ch has to be optimized by the user, gives the relative weight of this part as compared to the first part. The restriction supplied by eq. (4.3) gives the definition of the regression error. To solve this optimization problem, Lagrange function is constructed as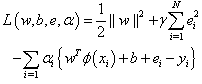 | (4.4) |
Where αi are the Lagrane multipliers. The solution of eq. (4.4) can be obtained by partially differentiating with respect to w, b, ei and αiThen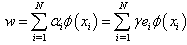 | (4.5) |
Where a positive definite Kernel is used as follows: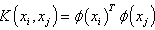 | (4.6) |
An important result of this approach is that the weights (w) can be written as linear combination of the Lagrange multipliers with the corresponding data training (xi). Putting the result of eq. (4.5) into eq. (4.1), the following result is obtained as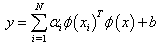 | (4.7) |
For a point 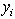 to evaluate it is:
to evaluate it is: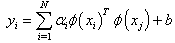 | (4.8) |
The vector follows from solving a set of linear equations: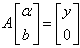 | (4.9) |
Where A is a square matrix given by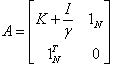 | (4.10) |
Where K denotes the kernel matrix with ijth element in eq. (4.5) and I denotes the identity matrix NN, 1N =[1 1 1…..1]T. Hence the solution is given by: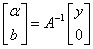 | (4.11) |
All Lagrange multipliers (the support vectors) are non-zero, which means that all training objects contribute to the solution and it can be seen from eq. (4.10) to eq. (4.11). In contrast with standard SVM the LS-SVM solution is usually not sparse. However, by pruning and reduction techniques a sparse solution can easily achieved.Depending on the number of training data set, either an iterative solver such as conjugate gradients methods (for large data set) can be used or direct solvers, in both cases with numerically reliable methods.In application involving nonlinear regression it is not enough to change the inner product of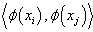 eq. (4.7) by a kernel function and the ijth element of matrix K equals to eq. (4.5).This shows the following nonlinear regression function:
eq. (4.7) by a kernel function and the ijth element of matrix K equals to eq. (4.5).This shows the following nonlinear regression function: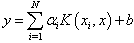 | (4.12) |
For a point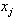 o be evaluated, it is:
o be evaluated, it is: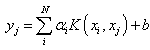 | (4.13) |
For LS-SVM, there are lot of kernel function (Radial basis function, Linear polynomial), sigmoid, bspline, spline, etc. However, the kernel function more used is a simple Gaussian function, polynomial function and RBF. They are defined by: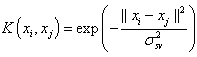 | (4.14) |
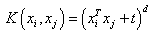 | (4.15) |
Where d is the polynomial degree and 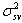 s the squared variance of the Gaussian function, to obtained support vector it should be optimized by user. In order to achieve a good generalization model it is very important to do a careful model selection of the tuning parameters, in combination with the regularization constant γ.
s the squared variance of the Gaussian function, to obtained support vector it should be optimized by user. In order to achieve a good generalization model it is very important to do a careful model selection of the tuning parameters, in combination with the regularization constant γ.
4. Result and Discussion
In this study, the proposed modelling are carried out; 25 sets of input-output patterns used for training both networks and for testing purpose the remaining 12 sets are used. The software programs developed are used for implementation using MATLAB version 10.1. In the beginning, SVM network was trained with commonly used kernels like Linear and RBF Kernel Function. Table(1-2) shows the performance of model means of Percentage of Classification rates(CR) obtained from the processing of testing data with respect to SVM and LS-SVM model with RBF kernel and Linear kernel. | Table 1. Confusion matrix for Test data sheet for SVM Modeling (using Linear Kernel Function) |
| | | True Class | | | | Predicted Class | Class-1(Boy) | Class-2(Girl) | Classification Rate(%) | | Class-1(Boy) | 5 | 2 | 67% | | Class-2(Girl) | 2 | 3 | |
|
|
| Table 2. Confusion matrix for Test data sheet for SVM Modeling (using RBF Kernel Function) |
| | | True Class | | | | Predicted Class | Class-1(Boy) | Class-2(Girl) | Classification Rate(%) | | Class-1(Boy) | 5 | 1 | 84% | | Class-2(Girl) | 1 | 5 | |
|
|
| Table 3. Confusion matrix for Test data sheet for LS-SVM Modeling (using Linear Kernel Function) |
| | | True Class | | | | Predicted Class | Class-1(Boy) | Class-2(Girl) | Classification Rate(%) | | Class-1(Boy) | 5 | 2 | 75% | | Class-2(Girl) | 1 | 4 | |
|
|
| Table 4. Confusion matrix for Test data sheet for LS-SVM Modeling (using RBF Kernel Function) |
| | | True Class | | | | Predicted Class | Class-1(Boy) | Class-2(Girl) | Classification Rate(%) | | Class-1(Boy) | 5 | 0 | 92% | | Class-2(Girl) | 1 | 6 | |
|
|
5. Conclusions
This paper proposes a gender classification from ECG signal using LS-SVM and SVM technique. The different input features extracted from HRV analysis are directly feed to SVM and LSSVM classifier. Both the classifiers are designed, trained and tested. LS-SVM classifier with RBF kernel gives better classification rate of 92% among other models. This shows LS-SVM as promising results for the classification of the Gender based on HRV and ECG signal analysis.
References
| [1] | Z.H Wang, Z.C Mu,” Gender classification using selected independent-features based on genetic algorithm” Proceedings of the Eighth International Conference on Machine Learning and Cybernetics, Baoding, 12-15 July 2009. |
| [2] | W. Bartkiewicz “Neuro-fuzzy approaches to short-term electrical load forecasting”,IEEE Explorer.vol 6, pages 229-234, 2000. |
| [3] | V. Vapnik, The Nature of Statistical Learning Theory, Springer, New York, 1995. |
| [4] | V. Vapnik, Statistical Learning Theory, Wiley, New York, 1998a. |
| [5] | V. Vapnik,“The support vector method of function estimation, In Nonlinear Modeling: Advanced Black-box Techniques, Suykens J.A.K., Vandewalle J. (Eds.), Kluwer Academic Publishers, Boston, pp.55-85, 1998. |
| [6] | J.A.K Suykens, T Van Gestel, J De Brabanter, B De Moor, J Vandewalle, Least Square SVM. Singapore: World Scientific, 2002. |
| [7] | D. Hanbay,“An expert system based on least square support vector machines for diagnosis of the valvular heart disease”, Expert Systems with Application, 36(4), part-1, 8368-8374.2009 |
| [8] | Z Sahli,,A.Mekhaldi, R.Boudissa, S.Boudrahem, “Prediction parameters of dimensioning of insulators under non-uniform contaminated condition by multiple regression analysis”, Electric Power System Research, Elsevier 2011 in press. |
| [9] | G. Zhu, D.G Blumberg, (2001) Classification using ASTER data and SVM Algorithms: The case study of Beer Sheva, Israel, Remote Sens. of Environ., 80, 233-240. |
| [10] | V. Kecman, (2005) Support Vector Machines: Theory and Applications Lipo Wang (Ed.) Support vector machine an introduction, Springer-Verlag Berlin Heidelberg,1-48. |
| [11] | V. Kecman, (2001) Learning and soft computing: Support vector machine, Neural network and Fuzzy logic models, MIT Press, Cambridge, MA, 148-176. |



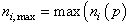 , p=1 …Np, i= 1….NiWhere ni(p) is the input features and Np is the number of patterns in the training set and testing set,
, p=1 …Np, i= 1….NiWhere ni(p) is the input features and Np is the number of patterns in the training set and testing set,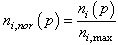 , p = 1….Np , i = 1,…NiAfter normalization, the input variables lie in the range of 0 to 1.
, p = 1….Np , i = 1,…NiAfter normalization, the input variables lie in the range of 0 to 1.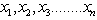 ) in n dimensional Space. A class decision function associated with Hyperplane is weighted sum of training data set and bias are symbolized[10, 11, 12] as
) in n dimensional Space. A class decision function associated with Hyperplane is weighted sum of training data set and bias are symbolized[10, 11, 12] as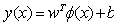
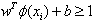
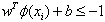
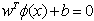
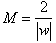 same as minimization of
same as minimization of 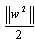
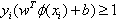
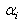 which is given as follows:
which is given as follows: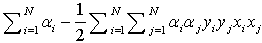
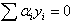 and
and 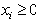 For all value of
For all value of 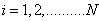 .After solving Quadratic optimization problem, the values of weight and bias are obtained as
.After solving Quadratic optimization problem, the values of weight and bias are obtained as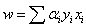
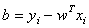
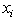 is support vector for each nonzero value of
is support vector for each nonzero value of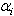 . Hence, the classification function for a test data point
. Hence, the classification function for a test data point 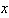 is inner product of support vector and test data point, which is given as follows
is inner product of support vector and test data point, which is given as follows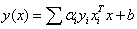
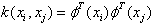
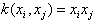 (Linear kernel Function)
(Linear kernel Function)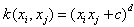 For
For 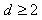 and
and 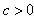 (Polynomial Kernel Function)
(Polynomial Kernel Function)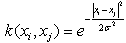 For
For 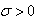 (Radial Gaussian kernel function)The new classification function using kernel function is defined as follows:
(Radial Gaussian kernel function)The new classification function using kernel function is defined as follows: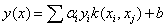
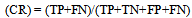
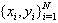 with input data
with input data 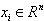 and corresponding binary class labels
and corresponding binary class labels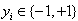 .The following Classification model can be constructed by using non-linear mapping function
.The following Classification model can be constructed by using non-linear mapping function 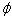 (x)[11].
(x)[11].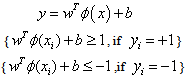
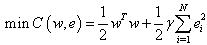
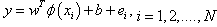
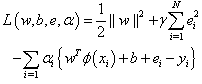
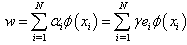
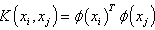
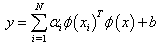
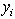 to evaluate it is:
to evaluate it is: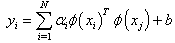
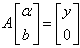
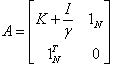
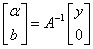
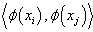 eq. (4.7) by a kernel function and the ijth element of matrix K equals to eq. (4.5).This shows the following nonlinear regression function:
eq. (4.7) by a kernel function and the ijth element of matrix K equals to eq. (4.5).This shows the following nonlinear regression function: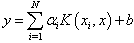
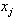 o be evaluated, it is:
o be evaluated, it is: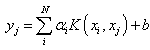
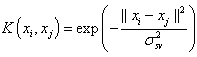
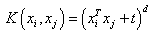
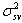 s the squared variance of the Gaussian function, to obtained support vector it should be optimized by user. In order to achieve a good generalization model it is very important to do a careful model selection of the tuning parameters, in combination with the regularization constant γ.
s the squared variance of the Gaussian function, to obtained support vector it should be optimized by user. In order to achieve a good generalization model it is very important to do a careful model selection of the tuning parameters, in combination with the regularization constant γ. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML