| [1] | Aapo Hyvärinen and Erkki Oja, “Independent Component Analysis: Algorithms and Applications”, Neural Networks Research Center, 13(4-5), 411-430, 2000. |
| [2] | Amar Kachenoura, Laurent Albera and Lotfi senhadji, “Séparation aveugle de sources en ingénierie biomédicale”, Article original, Science Direct ETSEVIER MASSON, ITBM-RBM 28, 20–34 (2007). |
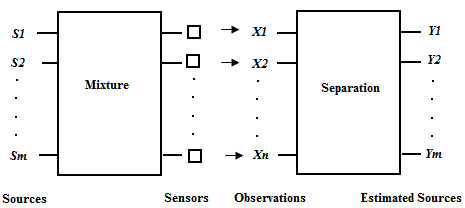
| [3] | Ali Mansour, Kardec A Barros, and Noboru Ohniski, “Blind separation of sources: Methods, assumptions and applications”, IEICE Trans. Fundamentals Electron. Commun. Comput Sci., vol. E83-A, no. 8, pp. 1498–1512, Aug. 2000. |
| [4] | Pierre Comon, Christian Jutten, " Séparation de sources 1 : concepts de base et analyse en composantes indépendantes ", Ed. Lavoisier, Paris 2007. |
| [5] | Pierre Comon, Christian Jutten, " Séparation de sources 2 : Au-delà de l'aveugle et applications ", Ed. Lavoisier, paris 2007. |
| [6] | K. Anand, G. Mathew, and V. Reddy, “Blind separation of multiple co-channel BPSK signals arriving at antenna array,” IEEE Signal Proc. Lett., vol. 2, no. 9, pp. 176–178, Sep. 1995. |
| [7] | E. Chaumette, Pierre Comon, and D. Muller, “ICA-based technique for radiating sources estimation: Application to airport surveillance,” Proc. Inst. Electr. Eng.—F, vol. 140, no. 6, pp. 395–401, Dec. 1993. |
| [8] | Lieven De Lathauwer, Bart De Moor, and Joos Vandewalle, “Fetal electrocardiogram extraction by source subspace separation,” in Proc. HOS, Aiguablava, Spain, Jun. 1995, pp. 134–138. |
| [9] | Scott Makeig, Anthony J Bell, Tzyy P Jung and Terrence J Sejnowski, “Independent component analysis of electroencephalographic data,” in Advances in Neural Information Processing Systems, vol. 8. Cambridge, MA: MIT Press, 1995. |
| [10] | Albert Bijaoui and Danielle Nuzillard, “Blind source separation of multispectral astronomical images,” in Proc. MPA/ESO/MPE Joint Astronomy Conf., A. J. Banday, A. Zaroubi, and A. Bartelmann, Eds. Garching, Germany: Springer-Verlag, 2000, pp. 571–581. 31/7-4/8. |
| [11] | Danielle Nuzillard and Albert Bijaoui, “Multispectral analysis, mutual information and blind source separation,” in Proc. 2nd Symp. Phys. Signal and Image Process., 2000, pp. 93–98. |
| [12] | M. Lennon, G. Mercier, M. C. Mouchot, and L. Hubert-Moy, “Spectral unmixing of hyperspectral images with the independent component analysis and wavelet packets,” in Proc. IGARSS Conf., Sydney, Australia, Jul. 9–13, 2001. |
| [13] | Mohamed A Loghmari, Mohamed S Naceur and Mohamed R Boussema, “A spectral and spatial source separation of multispectral images”. IEEE Trans. Geosci. Remote Sens.,vol. 44, no. 12, pp. 3659-3673, Dec 2006. |
| [14] | Jérôme Bobin, Jean L Starck, Jalal M Fadili, and Yassir Moudden, “Sparsity and Morphological Diversity in Blind Source Separation”, IEEE Trans. on Image Processing, vol. 16, pp. 2662-2674, Nov. 2007. |
| [15] | Jérôme Bobin, Jean L Starck, Yassir Moudden, and Jalal M Fadili, “Blind source separation : The sparsity revolution”, In Peter Hawkes, editor, Advances in Imaging and Electron Physics, volume 152, pages 221–298. Academic Press, Elsevier, 2008. |
| [16] | I.Gorodnitsky and Adel Belouchrani. Joint Cumulant and Correlation Based Signal Separation with Application to EEG Data, Proc. 3-rd Int. Conf. on Independent Component Analysis and Signal Separation , I:475-80, (2001). |
| [17] | Jean F Cardoso, “Blind signal separation: statistical principles” Proceedings of the IEEE. Special issue on blind identification and estimation, vol. 9, no. 10, pp. 2009–2025, Oct. 1998. |
| [18] | Adel Belouchrani, K. Abed Meriam, J.-F Cardoso and E. Moulines, “A blind source separation technique using second-order statistics” IEEE Transactions on Signal Processing, vol. 45, no. 2, pp. 434-444. Feb. 1997. |
| [19] | M. S Pedersen, J. Larsen, U. Kjems, and L. C. Parra, “A survey of convolutive blind source separation methods”, Springer Handbook on Speech Processing and Speech Communication”, ISBN 978-3-540-49125-5, 2007. |
| [20] | R.R. Gharieb, and A. Cichocki, “Second-order statistics based blind source separation using a bank of subband filters”, Digital Signal Processing 13 252–274 (2003) |
| [21] | Aapo Hyvärinen, “Survey on independent component analysis”, Neural Comput. Surveys 2, 94–128, (1999). |
| [22] | Aapo Hyvärinen, “New approximations of differential entropy for independent component analysis and projection pursuit”, Adv. Neural Inform. Process. Systems 10, 273–279 (1998). |
| [23] | S. Amari, A. Cichocki, H.H. Yang, “A new learning algorithm for blind signal separation”, Adv. Neural Inform. Process. Systems 8, 752–763 (1995). |
| [24] | S. Choi, A. Cichocki, A. Beluochrani, “Second order non-stationary source separation”, J. VLSI Signal Process. 32 (1/2) 93–104 (2002). |
| [25] | Danielle Nuzillard and Albert Bijaoui, “Blind source separation and analysis of multispectral astronomical images”, Astron. Astrophys. Suppl. Ser. 147, 129{138 (2000). |
| [26] | J.Wang and C.I Chang, “Independent component analysis-based Dimensionality Reduction with Applications in Hyperspectral Image Analysis”, IEEE TRANSACTIONS ON GEOSCIENCE AND REMOTE SENSING, VOL. 44, NO. 6, JUNE 2006. |
| [27] | J. Herault, Christian Jutten and B. Ans, «Détection de grandeurs primitives dans un message composite par une architecture de calcul neuromimétique en apprentissage non supervisé ». In: GRETSI 85, Dixième colloque sur le Traitement du Signal et des Images, Nice, France. p. 1017–22. (1985) |
| [28] | Christian Jutten, J. Herault, “Blind separation of sources, part: an adaptative algorithm based on neuromimatic architecture”; Signal Process; 24 (1):1–10. (1991). |
| [29] | Y. Li, D. Powers and J. Peach, “Comparison of Blind Source Separation Algorithms”, Mastorakis, Advances in Neural Networks and Applications, WSES (2000) p18-21. |
| [30] | Jean F Cardoso, Antoine Souloumiac, “Blind beam forming for non-Gaussian signals”. IEE Proceedings-F: radar and signal processing; 140(6): 362–70 (1993). |
| [31] | J Jean F Cardoso , Antoine Souloumiac, “Jacobi angles for simultaneous diagonalization”; SIAM J Matrix Anal Appl; 17(1):161–4 (1996). |
| [32] | Aapo Hyvärinen , Erkki Oja, “A fast fixed-point algorithm for independent component analysis. Neural Comput”; 9:1483–92 (1997). |
| [33] | Aapo Hyvärinen , J. Karhunen, P. Oja, “ Independent component analysis”, ser. New-York: Wiley Interscience. John Wiley and Sons; 2001. |
| [34] | M. Lennon, “Méthodes d’analyse d’images hyperspectrales, exploitation du capteur aéoroporté CASI pour les applications de carthographie aggro-environnementale en Bretagne (2002). |
| [35] | E. Christophe, “Compression des images hyperspectrales et son impact sur la qualité des données”, thèse (2006) |
| [36] | Jing M. Chen, Sylvain G. Leblanc, John R. Miller, Jim Freemantle, Sara E. Loechel, Charles L. Walthall, Kris A. Innanen, and H. Peter White, “Compact Airborne Spectrographic Imager (CASI) used for mapping biophysical parameters of boreal forests” in journal of geophysical research, vol. 104, no. d22, pages 27,945–27,958, November 27, 1999. |
| [37] | Adel Belouchrani, K. Abed-Meraim, Jean F Cardoso and E. Moulines « Second-order blind source separation of correlated sources ». In: International Conference on Digital and Signal. Cyprus: Nicosia; 1993. p. 346–61. |
| [38] | F.Ghaderi, H.R.Mohseni, S.Sanei, “ A fast second order blind identification method for separation of Periodic sources”; European Signal Processing Conference (EUSIPCO-2010). |
| [39] | M.S. Ould Mohamed, A. Keziou, H. Fenniri and G.Delaunay, “Niveau critère de séparation aveugle de sources cyclostationnaires au second ordre”; Revue ARIMA, vol. 12 (2010), pp. 1-14. |
| [40] | F. Gorodnitsky and A. Belouchrani, “Joint cumulant and correlation based signal separation with application to EEG data analysis”; National Science Foundation under Grant No. IIS. 0082119. |
| [41] | Jalal M Fadili, Jean L Stack, Jerome Bobbin, and Yassir Moudden, “Image decomposition and separation using sparse representations: an overview”. Proceedings of the IEEE, Special Issue: Applications of Sparse Representation, (2009) |
| [42] | P.D. O'Grady, B.A. Pearlmutter, S.T. Rickardy, “Survey of Sparse and Non-Sparse Methods in Source Separation”; IJIST (International Journal of Imaging Systems and Technology), 2005 |
| [43] | T. Gustafsson, U. Lindgren and H. Sahliny, “statistical analysis of a signal separation method based on second order statistics”; ICASSP Proceedings of the Acoustics, Speech, and Signal Processing, IEEE International Conference (2000) |
| [44] | C. Jutten and R. Gribonval, “L’Analyse en Composantes Indépendantes : un outil puissant pour le traitement de l’information” |
| [45] | Jérôme Bobin, Jean L Starck, Jalal M Fadili, and Yassir Moudden, “Sparsity and Morphological Diversity in Blind Source Separation”. IImage Processing, vol. 16, pp. 2662-2674, Nov. (2007) |
| [46] | Jérôme Bobin, Yassir Moudden, Jean L Starck, and M. Elad, “Morphological diversity and source separation” IEEE Signal Processing Letters, vol. 13, no. 7, pp. 409–412, (2006). |
| [47] | Jérôme Bobin, « Diversité morphologique et analyse de données multivaluées », thesis 2008 |
| [48] | Jalal Fadili, « Une exploration des problèmes inverses par les représentations parcimonieuses et l’optimisation non lisse », HDR, 2010. |
| [49] | J.M. Chen, S.G. Leblanc, J.R. Miller, J. Freemantle, S.E. Loechel, C.L. Walthall, K.A. Innanen, and H. Peter White, “Compact Airborne Spectrographic Imager (CASI) used for mapping biophysical parameters of boreal forests” in journal of geophysical research, vol. 104, no. d22, pages 27,945–27,958, november 27, 1999. |
| [50] | IGN data, 2005 |
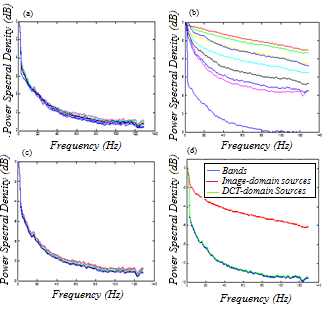
| [51] | Mohamed S Naceur, Mohamed A Loghmari and Mohamed R Boussema, “The contribution of the source separation method in the decomposition of mixed pixels” IEEE Trans. Geosci. Remote Sens., vol. 42, no. 11, pp. 2642-2653, Nov. 2004. |
| [52] | J. Liang and T. D. Tran, “Further results on DCT-based linear phase paraunitary filter banks. IEEE Trans. on Image Processing, vol. 2, pp. 681–684. Sept. 2002. |
| [53] | Alexander Ilin, Harri Valpola, and Erkki Oja, “Exploratory analysis of climate data using source separation methods” Elsevier Science, Reprinted with permission from Neural Networks, vol. 19, no. 2, pp. 155-167, Mar. 2006. |
| [54] | P. G. Georgiev, F. Theis, and A. Cichocki, “Sparse component analysis and blind source separation of underdetermined mixtures. IEEE Transactions on Neural Networks, vol. 16, no. 4, pp. 992–996, 2005. |
| [55] | Y.Tarabalka, Student, J.Benediktsson, and J.Chanussot, “Spectral–Spatial Classification of Hyperspectral Imagery Based on Partitional Clustering Techniques”, IEEE transactions on geoscience and remote sensing, vol. 47, no. 8, august (2009). |

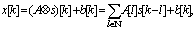
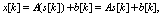
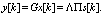
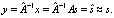
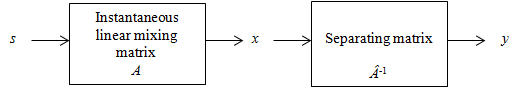
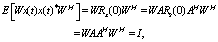
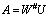
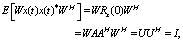
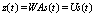
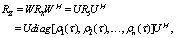
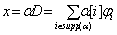
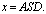

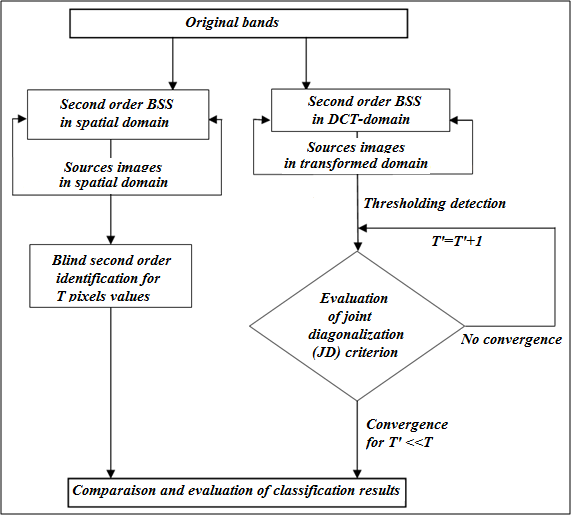
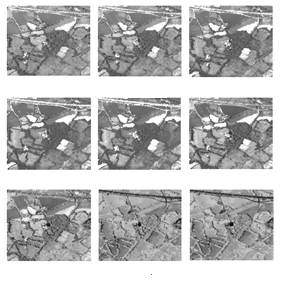

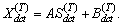
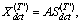
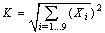
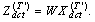
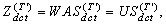
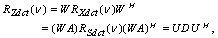
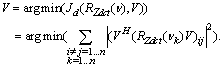
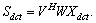
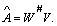
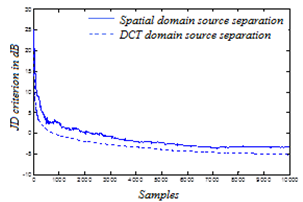
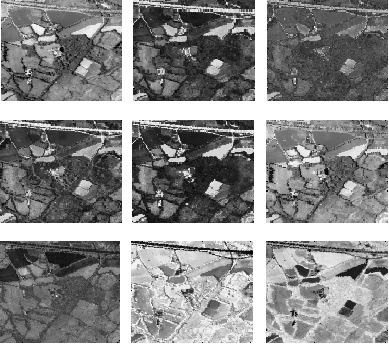
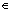 X and the hidden state c
X and the hidden state c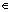 C. This statistical model must be estimated from the training set
C. This statistical model must be estimated from the training set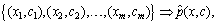
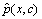 is the estimated distribution of conditional probability. The estimation of the joint probability
is the estimated distribution of conditional probability. The estimation of the joint probability 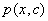 is the goal of this step, according to the information existing in the training set. The observed data are given as
is the goal of this step, according to the information existing in the training set. The observed data are given as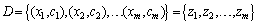
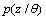 for modelling a set of data D. In assumption to be drawn independently from
for modelling a set of data D. In assumption to be drawn independently from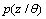 , the likelihood function can be modelled in the following form
, the likelihood function can be modelled in the following form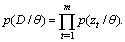
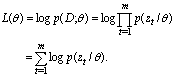
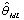 available to best explaining the examples by
available to best explaining the examples by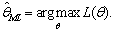
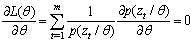
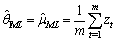
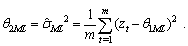
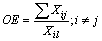
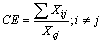
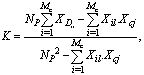
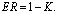
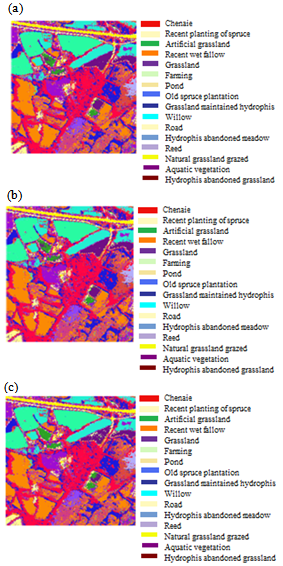
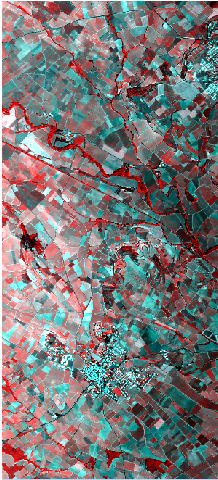

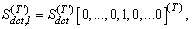
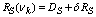
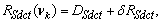
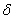 R=R(νk)-D.Then, from (33) we can have the following inequality
R=R(νk)-D.Then, from (33) we can have the following inequality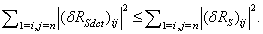
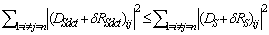
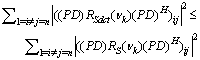
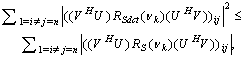
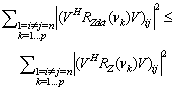
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML