Radhika Veerla 1, Zhengbing Zhang 1, 2, K. R. Rao 1
1Electrical Engineering Department, University of Texas at Arlington, Arlington, TX 76019, USA
2Electronics and Information College, Yangtze University, Jingzhou, Hubei, China
Correspondence to: K. R. Rao , Electrical Engineering Department, University of Texas at Arlington, Arlington, TX 76019, USA.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
JPEG is a popular DCT-based still image compression standard, which has played an important role in image storage and transmission since its development. Advanced Image Coding (AIC) is a still image compression system which combines the intra frame block prediction from H.264 with a JPEG-based discrete cosine transform followed by context adaptive binary arithmetic coding (CABAC), with best performance at low bit rates and has better performance than JPEG overall. In this paper, we propose a modified AIC (M-AIC) by replacing the CABAC in AIC with a Huffman coder and an adaptive arithmetic coder. The results were compared with other image compression techniques like JPEG using baseline method and JPEG2000, JPEG-LS and JPEG-XR in lossy compression, on various sets of test images. Simulation results are evaluated in terms of bit-rate, quality- PSNR and structural similarity index (SSIM). The simulation results based on PSNR demonstrate that M-AIC has optimal performance for images of all resolutions. The performance of still image codecs like M-AIC, JPEG-LS and JPEG-XR does not depend on the image resolution, which makes them suitable for wide varieties of applications. SSIM simulation results illustrate that M-AIC, JPEG2000 and JPEG-XR have similar performance and are better than any other codecs.
Keywords:
Adaptive Arithmetic Coding, Advanced Image Coding, Block Prediction, DCT, Huffman, JPEG, M-AIC, SSIM
Cite this paper:
Radhika Veerla , Zhengbing Zhang , K. R. Rao , "Advanced Image Coding and its Comparison with Various Still Image Codecs", American Journal of Signal Processing, Vol. 2 No. 5, 2012, pp. 113-121. doi: 10.5923/j.ajsp.20120205.04.
1. Introduction
JPEG[1] is a popular DCT-based still image compression standard, which has played an important role in image storage and transmission since its development. For instance, pictures taken by most of the current digital cameras are still in JPEG format, and as a result most of the images transferred on Internet are also in JPEG format. JPEG provides very good quality of reconstructed images at low or medium compression (i.e. high or medium bit rates respectively), but it suffers from blocking artifacts at high compression (low bit rates). Bilsen has developed an experimental still image compression system known as Advanced Image Coding (AIC) that encodes color images and performs much better than JPEG and close to JPEG-2000[2]. AIC combines intra frame block prediction from H.264 with a JPEG-style discrete cosine transform, followed by context adaptive binary arithmetic coding (CABAC) used in H.264. The aim of AIC is to provide better image quality with reduced complexity. It is also faster than existing JPEG2000 codecs. In this paper, a modified AIC (M-AIC) proposed in[3] is implemented and compared with various existing image codecs like JPEG[1], JPEG2000[8], JPEG-XR[9] and JPEG-LS[10] on various sets of test images. Although these compression techniques are developed for different signals, they work well for still image compression and hence worthwhile for comparison. The primary difference of the proposed M-AIC algorithm from AIC is that the CABAC is replaced by a Huffman coder and an adaptive arithmetic coder in order to reduce complexity of the algorithm. This paper considers JPEG only using baseline method and all the codecs are considered in lossy compression. The simulation results based on PSNR demonstrate that M-AIC performs much better than JPEG, outperforms JPEG-LS at low bit rates, performs close to AIC, JPEG-2000 and JPEG-XR. M-AIC is slightly better than AIC in very low bit rate range and outperforms.AIC, by ~3dB in case of gray scale images. For low resolution images, M-AIC performs better than JPEG 2000 and AIC takes the lead in this case. JPEG-XR, JPEG-LS has similar performance for all the image resolutions. Based on SSIM[13] simulations, it is observed that M-AIC, JPEG2000 and JPEG-XR give almost the best performance whereas JPEG is closer to the above codecs in performance with low complexity and JPEG-LS outperforms the above codecs in higher bit rate range.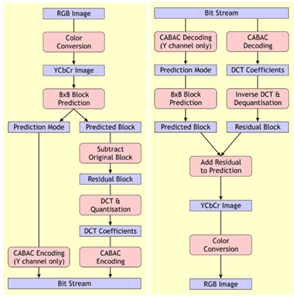 | Figure 1. The process flow of the AIC encoder and decoder[2] |
2. Overview of M-AIC Algorithm
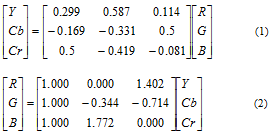 | (1) |
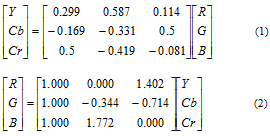 | (2) |
M-AIC[3] is based on JPEG structure to which prediction block similar to H.264 is added in order to achieve better compression. The AIC, shown in Fig. 1, and M-AIC shown in Figs. 2 and 3, are developed with the key concern of eliminating the artifacts, thereby increasing quality. The predictor is composed of five parts including IDCT, inverse quantization, Mode Select and Store, Block Predict and an Adder. The function of the predictor is to predict the current block to be encoded with the previously decoded blocks of the upper row and the left column. AIC uses CABAC entropy coding which uses position of the matrix as the context; while the M-AIC takes up Huffman coding and adaptive arithmetic coding in combination in order to achieve similar performance and also to reduce complexity.
2.1. M-AIC Encoder
M-AIC uses a DCT based coder, shown in Fig. 2. DCT coding framework is competitive with wavelet transform coding if the correlation between neighboring pixels is properly considered using entropy coding. This is applied in M-AIC.Here, the original image is converted from RGB domain to YCbCr domain in 4:4:4 sampling format. Equation 1 refers to the color conversion matrix from RGB to YCbCr and equation 2 refers to color conversion matrix from YCbCr to RGB.The YCbCr blocks are divided into 8x8 non-overlapping blocks which are encoded block by block in zig-zag scan order whereas the Bilsen’s AIC[2] uses scan-line order. 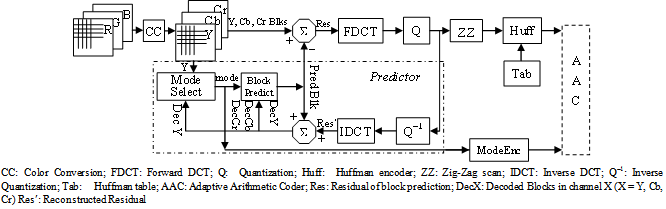 | Figure 2. M-AIC encoder[3] |
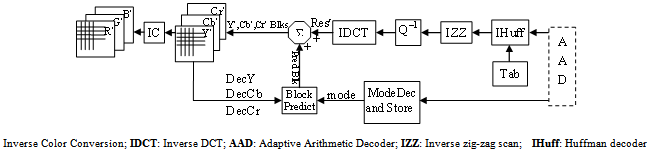 | Figure 3. M-AIC decoder[3] |
This is followed by encoding each block in all the channels. While encoding each block in Y channel select a block prediction mode first, which minimizes the prediction error measured with sum of absolute difference (SAD), by performing full search among the predefined 9 intra-prediction modes in[3]. The 9 block prediction modes, Mode 0 through Mode 8, represent vertical, horizontal, DC, diagonal down-left, diagonal down-right, vertical-right, horizontal-down, vertical-left and horizontal-up predictions respectively. The same selected prediction mode which is used to store and predict the current block in Y is used for corresponding Cb and Cr blocks. The prediction residual (Res) of the block to be encoded is transformed into DCT coefficients using a fast floating point DCT algorithm. Then the DCT coefficients are uniformly scalar-quantized. The same quantization parameter (QP) is used to quantize the DCT coefficients of Y, Cb and Cr channels and transferred into a one-dimensional sequence with a zig-zag scan order. All the 64 coefficients including both the DC coefficient and the AC coefficients are encoded together with the same algorithm as that for encoding the AC coefficients in JPEG standard. The proposed M-AIC algorithm makes use of the chrominance-AC-coefficient Huffman table recommended in baseline JPEG to encode all channels of Y, Cb and Cr[1][4]. Then the selected prediction modes are encoded with a variable length code. If the prediction mode of the current block is the same as that of the previous block, output only 1 bit of 0, else output 1 bit of 1 followed by 3 bits of the mode number message, which is the mode index itself or the mode index minus 1 if the mode index of the current block is less than or greater than that of the previous block respectively. To form a compressed stream, 11 bytes are used to construct a stream header including stream format flag, algorithm version, quantization parameter (QP), image width, image height, pixel bit-count of the original image, and the code size of the compressed modes. The compressed bit-stream is orderly composed of the header, the code of the prediction modes, the Huffman codes of Y-Res, the Huffman codes of Cb-Res and the Huffman codes of Cr-Res. An adaptive arithmetic coder (AAC) is added at the end of the encoder. The AAC[11] is fed with 8-bit symbols extracted byte-by-byte from the compressed stream (the header, the code of the prediction modes, and the Huffman codes of Y-Res, Cb-Res and Cr-Res) resulting in final bit stream.
2.2. M-AIC Decoder
The M-AIC decoding process shown in the Fig. 3 is reverse of encoding. The coded bit-stream from the encoder is fed to AAD resulting in the stream header, the code of the prediction modes and the Huffman codes of the Y-Res, Cb-Res and Cr-Res. The code of the prediction modes is decoded into prediction modes and stored. The residual of the current block is obtained by a decoding algorithm similar to baseline JPEG decoder[4]. The prediction of the current block is produced from the previously decoded blocks according to its prediction mode. The reconstructed residual is added to the prediction to result in the reconstructed current block. After the reconstruction of all the Y′, Cb′ and Cr′ blocks, they are converted back to RGB domain.
3. Codecs Used In Comparison
Transformation and coefficient encoding are the main blocks of all the codecs which play a significant role in defining the compression quality of the system[12]. Now, let us look at various codecs and their structures to study their impact on the compression quality and reconstruction. The reconstruction includes how each method is designed to avoid different kinds of artifacts. JPEG standard[1] is used in popular baseline mode which supports only lossy compression and gives good compression results with least complexity. It is based on block based 8x8 DCT followed by uniform quantization, zig-zag scanning and Huffman entropy coding. JPEG2000 standard[8] is considered for lossy compression. It is based on discrete wavelet transform, scalar quantization, context modeling, arithmetic coding and post compression rate allocation. JPEG 2000 provides for resolution, SNR, parseable code-streams, error-resilience, arbitrarily shaped region of interest (ROI), random access (to the sub-band block level), lossy and lossless coding, etc., all in a unified algorithm. JPEG-XR standard[9] which supports HD photo file format is designed explicitly for next generation of digital cameras and for storage of continuous-tone photographic content based extensively on Microsoft HD photo technology[6]. It shares some of the features from JPEG2000 like bit-rate scalability, editing, region-of-interest coding, integer implementation without division etc. HD photo is a block-based image coder: color conversion, reversible integer-to-integer-mapping lapped bi-orthogonal transform (LBT), adaptive coefficient scanning, flexible scalar quantization, inter-block coefficient prediction and adaptive VLC table switching for entropy coding. JPEG XR[9] supports a number of advanced pixel formats in order to avoid limitations and complexities of conversions between different unsigned integer representations allowing flexible approach to numerical encoding of image data enabling it to be used for low- complexity implementations in the encoder and decoder. JPEG-LS standard[10] is based on LOCO-I algorithm proposed by Hewlett Packard. JPEG-LS is based on prediction, context modeling and Golomb coder. JPEG-LS is used in near-lossless mode where the reconstructed image component is differed from original by a factor “NEAR”. The near-lossless compression has the feature to increase the compression ratio and speed of execution by specifying the tolerance error. It works well for cost sensitive applications which do not need ROI and error resilience. The result of applying spatial prediction and wavelet like 2-level transform iteration is effective in smooth image regions.
4. Simulation Results and Analysis
4.1. Codec Setting
In the coding simulations, publicly available software implementations are used for AIC, JPEG-baseline, JPEG2000, HD photo and JPEG-LS. For JPEG, JPEG baseline reference software[4] is used. This software can handle image data in many formats like PGM/PPM, GIF, windows BMP. For JPEG 2000, “JasPer” (version 1.900.1) software[5] is used. This software can handle image data in many formats like PGM/PPM, windows BMP, but it does not accept all the BMP files. In JPEG 2000, it is used to code each frame to reach target rate specification in terms of compression factors, which is well defined for multi-component images. HD photo reference software[6] supports BMP, TIF and HDR formats. Both JPEG and HD photo reference softwares are used to code each frame to reach the target quality factor that indirectly controls bit rate for lossy coding. JPEG-LS reference software[7] provided by HP labs is used for lossy compression. It supports only PGM/PPM image formats as input to the encoder and JLS format as output at the encoder.For Microsoft HD Photo[6], all options are set to their default values with the only control coming from the quality factor setting:• No tiling• One-level of overlap in the transformation stage• No color space sub-sampling• Spatial bit-stream order• All sub-bands are included without any skippingWMPEncApp command line converts certain uncompressed file formats into equivalent HD photo files. WMPDecApp command line converts HD photo files to different uncompressed file formats. The settings for JPEG-LS software[7] are as follows at the encoder. Decoder settings need not be changed from default as they follow the encoder settings.• Images should be in ppm or pgm format.• Line interleaved mode is considered in the project.  | Figure 4(a). Original Image |
 | Figure 4. (b) M-AIC with quantization parameter – 90, 0.12bpp, 25.84dB, (c) AIC with quality –7,0.12bpp, 26.19dB, (d) JPEG-baseline with quality - 5, 0.22bpp, 24.29dB |
 | Figure 4. (e) JPEG2000 with rate - 0.005, 0.12bpp, 27.68dB, (f) JPEG-XR with quality – 86, 0.12bpp, 27.49dB, (g) JPEG-LS with error value – 40, 1.02bpp, 22.17dB |
 | Figure 5. (a) M-AIC with quantization parameter – 90, 0.12bpp, M-SSIM – 0.636, (b) AIC with quality – 7, 0.12bpp, M-SSIM –0.6149, (c) JPEG-baseline with quality - 5, 0.22bpp, M-SSIM – 0.5886 |
 | Figure 5. (d) JPEG2000 with rate - 0.005, 0.12bpp, M-SSIM - 0.6844 (e) JPEG-XR with quality – 86, 0.12bpp, M-SSIM – 0.6755, (f) JPEG-LS with error value – 40, 1.02bpp, M-SSIM – 0.444 |
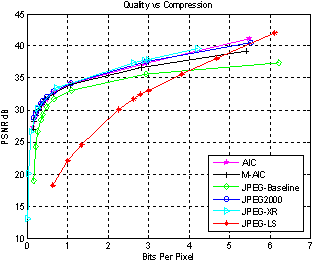 | Figure 6. (a) Simulation results for Lena (512x512x24) image based on PSNR |
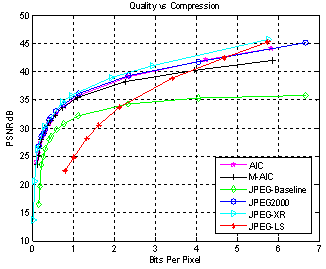 | Figure 6. (b) Simulation results for Airplane (512x512x24) image based on PSNR |
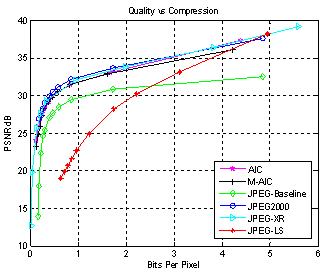 | Figure 6. (c) Simulation results for Peppers (512x512x24) image based on PSNR |
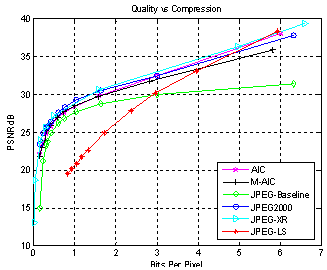 | Figure 6. (d) Simulation results for Sailboat on Lake (512x512x24) image based on PSNR |
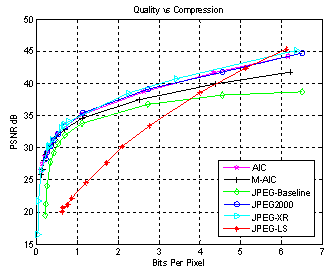 | Figure 6. (e) Simulation results for Couple (256x256x24) image based on PSNR |
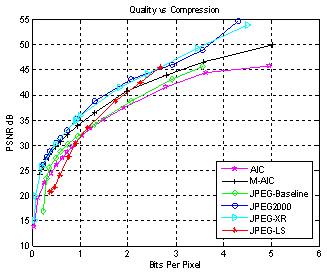 | Figure 6. (f) Simulation results for Cameraman (256x256x8) image based on PSNR |
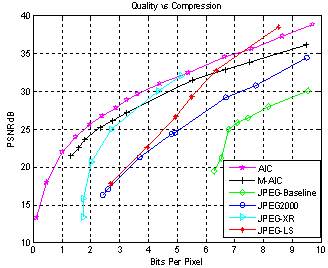 | Figure 6. (g) Simulation results for Lena (32x32x24) image based on PSNR |
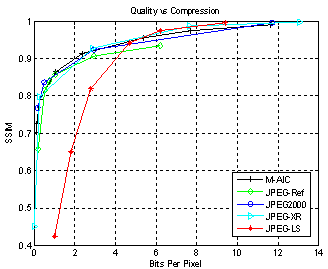 | Figure 7. Simulation results for Lena (512x512x24) image based on SSIM |
| Table 1. Simulation Results For Lena (512x512x24) Image |
| | M-AIC | | | | | | Quantization parameter | Encoded image size | bit rate | PSNR | SSIM | | 1 | 384142 | 11.65 | 44.11 | 0.9903 | | 2 | 253035 | 7.72 | 41.39 | 0.975 | | 3 | 177223 | 5.41 | 39.21 | 0.955 | | 5 | 96647 | 2.37 | 36.61 | 0.914 | | 10 | 30246 | 1.07 | 34.01 | 0.864 | | 30 | 8894 | 0.27 | 30.16 | 0.791 | | 70 | 4998 | 0.15 | 26.91 | 0.726 | | 90 | 3985 | 0.12 | 25.61 | 0.702 |
|
|
• Error value is varied from 1 to 60. Error value of zero corresponds to no compression.• T1, T2, T3 are thresholds. While giving the settings the following condition need to be met. Error value+1• Default RESET value of 64 is considered in this paper.
4.2. Simulation Results Explained
Based on the SSIM metric for Lena image of (512x512) image resolution, M-AIC, JPEG2000 and JPEG-XR almost perform the best over the entire bit range; JPEG follows the above codecs but has low dynamic range. JPEG-LS follow the above trend for higher bit ranges. JPEG differs from M-AIC by 0.02 SSIM scale. Between 4 and 12bpp range, JPEG-XR performs the best, followed by M-AIC and JPEG2000. JPEG-LS has better performance than JPEG2000 at above 4.8bpp and better than M-AIC at above 5bpp. It outperforms any other codec at above 6bpp. Table I shows the simulation results of M-AIC based on PSNR and SSIM for varying quantization parameter. The table demonstrates how well the quality index represents the change in the image with respect to change in bit rate. Complexity is defined by number of additions, multiplications and memories, but it is difficult to determine in this way. So for simplicity, encoding time is used to determine complexity. Several elements like transform and encoder contribute to the system complexity. JPEG is considered fastest algorithm as it has no intra-prediction. M-AIC uses intra-prediction, DCT, Huffman coding and adaptive arithmetic coding which makes it slower than JPEG but faster than AIC which is implemented using CABAC.The proposed deblocking filter can be implemented in a real time system. By doing so, its exact reduction in implementation complexity compared to JM 9.8 can be determined. The deringing filter[10] can also be incorporated in the in-loop filter to see the visual improvement of the reconstructed video. The proposed method uses image enhancement techniques to reduce the artifacts in the reconstructed video. Image recovery techniques can also be explored to reduce the artifacts in H.264 decoded video. Also, the transforms that do not produce blocking artifacts as well as providing the benefits of integer DCT can be explored.| Table 2. Evaluation Of Complexity For Lena (512x512x24) Image |
| | Lena (512x512x24) for 0.48bpp | Average encoding time in ms | | JPEG2000 | 911.9 | | M-AIC | 453.1 | | JPEG | 117 | | JPEG-XR | 363.5 |
|
|
JPEG is 3 times faster than JPEG-XR, 4 times faster than M-AIC and 8 times faster than JPEG2000. AIC makes use of intra prediction and CABAC encoding process; CABAC has higher complexity due to its inherent data dependency[14]. The complexity in JPEG2000[8] is due to its use of lot of scans to construct embedded zero-trees making it more complex than M-AIC. M-AIC has half the encoding time than JPEG2000. One of the reasons for the complexity of JPEG-XR is because of its bi-orthogonal lapped transform whose complexity is higher than DCT[15]. M-AIC is 1.25 times more complex than JPEG-XR. JPEG, AIC and M-AIC use DCT; and therefore their complexity are further not increased because of the transform structure. The main advantage of JPEG is its low complexity and hence preferred in low complexity applications. The reference softwares of AIC and JPEG-LS do not provide the encoding time and hence cannot be compared.
5. Conclusions and Future Work
The M-AIC algorithm was successfully implemented to obtain better compression with reduced complexity compared to existing codecs in terms of PSNR and best performance at low bit rates in addition to being competitive with any other codec in terms of SSIM over the entire bit range. The proposed algorithm is compared with JPEG reference software[4], JPEG-2000 JasPer software[5], JPEG-XR HD-photo reference software[6] and JPEG-LS LOCO-I software[7]. Thus by its performance, it finds wide range of applications in digital camera market, internet browsing, multimedia products such as mobile phones and entertainment appliances. From the results, it is observed that M-AIC is suitable for web images as it gives best outputs for low resolution images. This algorithm can be extended to compare the lossless compression. The implementation of CABAC can be a future study.
References
| [1] | W. B. Pennebaker and J. L. Mitchell, JPEG still image data compression standard, Van Nostrand Reinhold, New York, 1993. |
| [2] | AIC website: http://www.bilsen.com/aic/ |
| [3] | Z. Zhang, R. Veerla and K. R. Rao, “A modified advanced image coding”, to appear in Proceedings of CANS’ 2008, Romania, Nov. 8-10, 2008. |
| [4] | JPEG reference software website:ftp://ftp.simtel.net/pub/simtelnet/msdos/graphics/jpegsr6.zip |
| [5] | JPEG 2000 reference software: “JasPer version 1.900.1” on website: http://www.ece.uvic.ca/~mdadams/jasper/ |
| [6] | Microsoft HD photo specification:http://www.microsoft.com/whdc/xps/wmphotoeula.mspx |
| [7] | JPEG-LS reference software websitehttp://www.hpl.hp.com/loco/ |
| [8] | M. D. Adams, “The JPEG-2000 still image compression standard”, ISO / IEC JTC 1/SC 29/WG 1 N2412, Dec. 2005. |
| [9] | G. J. Sullivan, “ ISO/IEC 29199-2 (JpegDI part 2 JPEG XR image coding – Specification),” ISO/IEC JTC 1/SC 29/WG1 N 4492, Dec. 2007 |
| [10] | M.J. Weinberger, G. Seroussi and G. Sapiro, “The LOCO-I lossless image compression algorithm: principles and standardization into JPEG-LS”, IEEE Trans. Image Processing, vol. 9, pp. 1309-1324, Aug. 2000. |
| [11] | I. H. Witten, R. M. Neal and J. G. Cleary, “Arithmetic coding for data compression,” Communications of the ACM, vol. 30, pp. 520-540, June 1987. |
| [12] | T. Tran, L.Liu and P. Topiwala, “Performance comparison of leading image codecs: H.264/AVC intra, JPEG 2000, and Microsoft HD photo,” Proc. SPIE Int’l Symposium, Digital Image Processing, San Diego, Sept. 2007. |
| [13] | Z. Wang et al., “Image quality assessment: from error visibility to structural similarity,” IEEE Trans. Image Processing, vol. 13, pp. 600-612, Apr. 2004. |
| [14] | C. Lo, Y. Zeng and M. Shieh, “Design and test of a high-throughput CABAC encoder”, IEEE region 10 conference, pp. 1-4, Oct. 2007. |
| [15] | H. S. Malvar, “Biorthogonal and non-uniform lapped transforms for transform coding with reduced blocking and ringing artifacts”, IEEE Trans. Signal Processing, Special issue on theory and application of filter banks and wavelet transforms, vol. 46, pp. 1043 – 1053, April 1998. |

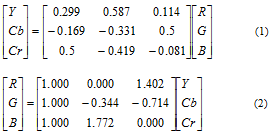
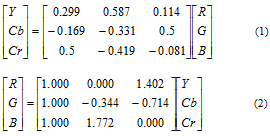















 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML