-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
2012; 2(4): 76-82
doi: 10.5923/j.ajsp.20120204.04
Genetic Algorithm Clustering for Color Image Quantization
F. Z. Bellala Belahbib , F. Souami
LRIA Département Informatique FEI, USTHB, Alger, Algérie
Correspondence to: F. Z. Bellala Belahbib , LRIA Département Informatique FEI, USTHB, Alger, Algérie.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Clustering is an unsupervised classification method used for different issues in image analysis. Genetic algorithms are randomized search and optimization techniques. In this paper, we present a genetic algorithm clustering for color image quantization as a prior process to any other one for image analysis. A fitness function with a smallest number of variables is proposed. It’s based on the fuzzy c-means objective function reformulated by Bezdek and the one proposed by Frigui and Krishnapuram in their competitive agglomeration algorithm. In the proposed clustering genetic algorithm, variable chromosome length is used to adjust the clusters number and determine their centers at the same time. Application of the algorithm to color image quantization shows that initial population solutions converge to good results. Furthermore, results in different color spaces and impact of parameters are discussed.
Keywords: Genetic Algorithms, Clustering, Fuzzy Clustering, Color Image Quantization
Article Outline
1. Introduction
- Genetic algorithms are randomized search andoptimization techniques[11] inspired by natural species evolution. They converge toward global solution and are parallelized. In genetic algorithms, population of solutions or individuals is encoded in the form of chromosomes (strings). Individuals are randomly initialized from a large search space and coded (often in binary). This population is then evolved from generation to other using genetic operators: crossover, mutation and selection. The selection operation depends on an objective function called fitness (or evaluation function) which measures the goodness of the solution. The process of selection, crossover and mutation are continually applied for individuals till termination conditions are satisfied or a fixed number of generations is reached.Clustering is an unsupervised classification technique where elements in the same class (cluster) are as similar as possible and elements in different classes are as dissimilar as possible. A most popular clustering algorithm is the K-Means. It allows a partition of set of elements into a set of K clusters such that the squared error between the empirical mean of a cluster and the points in the cluster isminimized [6]. One variant of K-Means is the Fuzzy C-Means (FCM) where principal of fuzzy sets is used. In FCM algorithm, one element can be in more than a cluster with different memberships. Given a set of data, a set of class centers and a partition matrix, the FCM algorithm consists in updating the centers values and the partition matrix till convergence. Validity index was introduced[18],[19] to select clusters number optimal value after applying the algorithm for different initialization schemes. However, FCM algorithm is very sensitive to initialization parameters and can lead to local minima instead of global one.On the other hand, it has been proved that GeneticAlgorithms as stochastic approaches converge generally to the global solution even with complex data. Genetic algorithms have been applies with satisfactory results for data clustering. Maulik and Bandyopadhyay have demonstrated the effectiveness of GA for clustering artificial data sets in[1,11] and for pixel classification in[12] using different validity index as a measure of the fitness function and different configurations of cluster centers as individuals of population coded in real values. Wang use GA to determine the number of cluster centers and there coordinates in[17] with binary codification of individuals where each bit in one individual indicates either an associated data is center or not center. The GA results are then filling to FCM algorithm to cluster the no centers data. Scheunders has described a hybrid clustering algorithm combining GA with C-Means algorithm in[16] using cluster centers as individuals and the inverse of MSE (Mean Squared Error) as fitness function. It has been shown that author’s approach gives good results.These propositions were applied for simple data or for grayscale images. In this paper, we propose a geneticalgorithm for data clustering using a variable chromosome length as in[12] and we demonstrate its efficiency for color image quantizing.This paper is organized as follows. In section two, we present briefly the FCM clustering algorithm. In the third section, we present our algorithm, the chromosomecodification, the fitness function and the evolution operations. In the last section, we present the results obtained by applying our algorithm for color image quantization. And we finally, conclude our work.
2. FCM Clustering
- Clustering is the unsupervised classification of patterns (observations, data items, or feature vectors) into groups (clusters)[7]. In image analysis, partitional algorithms for clustering are the most preferred. They have been applied for classification, segmentation[13] and image retrieval[8]. The most popular and simplest partitional algorithm is K-Means also known as hard clustering. It allows the allocation of a single cluster to each data. In opposite, the FCM algorithm for clustering which is a fuzzy version of K-Means, introduced by Ruspini in 1969[15] and enhanced by Bezdek[2], allows uncertain classifications, which made it more flexible and more appropriate to natural phenomena. FCM method assigns degrees of membership in several clusters to each input pattern and can be converted to a hard clustering by assigning each pattern to the cluster with the largest measure of membership[7].Formally, given a data set X = {xj, j=1,…, N} and let C be the number of clusters. The FCM algorithm evolves the centers βi of set B={βi, i=1, …, C} defined by the Eq.1 for each class i
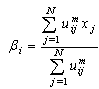 | (1) |
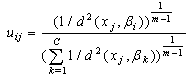 | (2) |
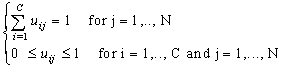 | (3) |
3. Genetic Algorithm Clustering
- Genetic algorithms are stochastic optimization methods based on biological evolution of natural species founded by J. Holland in 1975[14]. The principal steps of classical genetic algorithms can be summarized as follows:
 | Figure 1. GA Steps |
3.1. Chromosomes Encoded and Initialization
- Binary coding is the most common representation of strings in GA. But it has been proved that real representation is more suitable and more efficient[3,11]. The chromosomes in this paper are encodes with real values.Each gene chromosome is a three dimensional vector (to get color image feature for our application) and each coordinate take real value. Variable string length is used to find the clusters number C and the centers βi without any prior knowledge. We must just initialize the string length to the maximum possible number of clusters. This number might be adjusted with processing and the invalid item (item which is not center) in each chromosome is represented by an invalid value (negative value as an example for the RGB color representation). The initial string length depends on the precision desired by clustering or the precision required for the image analysis step that follows the quantization for our application.The values of each chromosome k (k=1...P) are randomly chosen from the data set to be clustered what allows convergence in fewer generations. For quantization, one chromosome is a set of colors of randomly chosen pixels of a given image and some arbitrary genes are made to invalid value.
3.2. Fitness Function
- The standard FCM algorithm is based on the minimization of the objective function noted J by Bezdek et al. in[2] and by Hathaway and Bezdek in[8] and defined by:
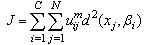 | (4) |
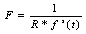 | (5) |
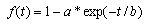 | (6) |
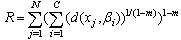 | (7) |
3.3. Selection
- The selection operation determines the survival individuals for the next generation according to their fitness value. In this paper, we use the roulette wheel selection method[9] to choose the individuals to be crossed and mutate. In addition, some parent individuals are kept for the next generation to preserve good characteristics and to avoid premature convergence.
3.4. Crossover and Mutation Operations
- The crossover operation consists in interchange parts of two randomly chosen parent chromosomes to generate child chromosomes. The crossover operation may be in one or more randomly chosen point. In our algorithm, a one-point crossover is applied with a probability pc=0.82 at a chromosome position upper then 1 and less then the chromosome length. Note that gene is a three dimensional vector and it can not be truncated. Mutation is the operation which alters (mutates) a gene at a random position in chromosome chosen with a small probability pm. In this paper pm=0.01. Indeed, the objective is to find the best combination of features points in image space which can represent the centers without trying calculating them. So the mutation probability may be smaller.
3.5. Stop Condition
- The process of selection, crossover and mutation is iterated for a finite number or until individuals converge to practically the same one. The best chromosome is then taken from the last generation and is used as solution for the clustering problem. Therefore the length of this chromosome gives the clusters number and genes values their centers.
4. Application to Color Image Quantization
- We applied the genetic algorithm described above to color image quantization. Quantizing color image consists to find at first a new color palette with a reduced number of colors than the original one (2563 for 24 bits RGB image) and then assign each pixel point of original image to one of the color in the new palette. The color image quantization algorithms are classified into two classes[16]. The first class contains methods based on splitting algorithms and the second one consists of clustering based methods. In the previous sections, we have presented a clustering algorithm witch can effortlessly be applied for quantization such that the best chromosome generated by the proposed GA represents the palette obtained and each image pixel is assigned to its new color by the argmin function (the nearest color according to a given metric).Images from the Berkeley images base[10] and other famous images are used to evaluate the proposed algorithm. The images are 24bits/pixel real color images. Quantization is evolved in four different color spaces, the RGB, XYZ and Lab and Luv as perceptual ones[5]. Examples of the obtained results in RGB color space are shown in figure 2 after 17 generations and 60 genes (colors) as initial string length where original images are presented in the first row (a, d and g) and the quantized ones in the third row (c, f, and i). The MSE value is used to evaluate difference between original images and the quantized ones.In addition, quantized images by the CA algorithm are presented for comparison in figure 2 second row (b, e and h). The CA algorithm is applied with 60 initial values of clusters (to allow comparison). In both of them (CA algorithm and the proposed GA), Euclidean distance is used and the value of the constants ‘a’ and ‘b’ are taken to be 5 and 10 as in[4]. For the propped algorithm, the degree of fuzzification m is fixed to 3, the population size is taken to be 100 (P=100) and the initial string length is equal to 60 for the presented images. Other results are also shown in figure 3, 4 and 5 for ‘Peppers’, ‘House’ and ‘Lion’ images with m=2.
 | Figure 2. Quantized images from Berkeley images base |
 | Figure 3. Quantized ‘Peppers’ image by CA and proposed GA |
 | Figure 4. Quantized ‘House’ image by CA and proposed GA |
 | Figure 5. Quantized ‘Lion’ image by CA and proposed GA |
| ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
 | Figure 6. Quantized images in different color spaces with 32 colors and 64 colors as initial string length |
5. Conclusions
- Clustering is an unsupervised classification algorithm commonly used in image analysis. Genetic algorithms are a heuristic technique optimization. Even if they are time consuming, it’s proved that they converge nevertheless in better results. In this paper, a clustering method based on genetic algorithm is proposed. It permits to find the clusters number without using validity indices and it requires fewer variables for the fitness function. The application of this algorithm to image quantization proves its efficiency. In addition, if local constraints between neighboring pixels are taken into account, the approach can load to important results for image segmentation process. Currently works are in progress using this genetic algorithm applied for color images to achieve segmentation process in less run-time and may succeed this paper.
References
| [1] | S. Bandyopadhyay and U. Maulik, “Nonparametric Genetic Clustering: Comparison of Validity Indices”, IEEE Transactions on Systems, Man, and Cybernetics - Part C: Applications And Reviews, vol. 31, no. 1, February 2001 |
| [2] | J. C. Bezdek, J. Keller, R. Krisnapuram, N. Pal, Fuzzy Models and Algorithms For Pattern Recognition and Image Processing, Kluwer Academic Publishers, 1999. |
| [3] | D. B. Fogel, Evolutionary Computation. Toward a new philosophy of machine intelligence, 3rd ed., IEEE Press, 2006. |
| [4] | H. Frigui and R. Krishnapuram, “Clustering by competitive agglomeration”, Pattern Recognition, vol. 30, Issue 7, pp. 1109-1119, July 1997. |
| [5] | T. Gevers, Color Image Invariant Segmentation and Retrieval. PhD thesis, University of Amsterdam, The Netherlands, May 1996. |
| [6] | A. K. Jain, “Data Clustering: 50 years beyond K-means”, Pattern Recognition Letters, vol. 31, no. 8, pp. 651-666, June 2010. |
| [7] | A.K. Jain, M.N. Murty And P.J. Flynn, “Data Clustering: A Review”, ACM Computing Surveys, vol. 31, no. 3, September 1999. |
| [8] | R. J. Hathaway, J. C. Bezdek, “Optimization of clustering criteria by reformulation”, IEEE Transactions on Fuzzy Systems vol. 3, no. 2, pp. 241–254, 1995. |
| [9] | E. Lutton, P. Martinez, “A Genetic Algorithm for the Detection of 2D Geometric Primitives in Images”, 12th International Conference on Pattern Rocognition, ICPR, Jerusalem, Israel, S. Ulman, S. Peleg (gen. Co-chairs), Octobre 9-13, 1994, IEEE Computer Society: Los Alamitos, CA, 1994. |
| [10] | D. Martin, C. Fowlkes, D. Tal and J. Malik, “A Database of Human Segmented Natural Images and its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics”, ICCV, vol. 2, pp. 416-423, 2001. |
| [11] | U. Maulik and S. Bandyopadhyay, “Genetic Algorithm Based Clustering Technique”, Pattern Recognition, vol. 33, no. 9, pp. 1455-1465, 2000. |
| [12] | U. Maulik and S. Bandyopadhyay, “Fuzzy Partitioning Using Real Coded Variable Length Genetic Algorithm for Pixel Classification”, IEEE Transactions on Geosciences and Remote Sensing, vol. 41, no. 5, pp. 1075-1081, 2003. |
| [13] | S. Philipp-Foliguet, M. Bernardes Viera, M. Sanfourche, “Fuzzy Segmentation of Color Images and Indexing of Fuzzy Regions”, CGIVl, Poitier, pp. 507-512, 2002. |
| [14] | C. R. Reeves, Chapter 5 of: Handbook of Metaheuristics, M. Gendreau, J. Y. Potvin (eds.), International Series in Operations Research & Management Science 146, Springer Science+Business Media, LLC 2010 |
| [15] | E. H. Ruspini, “A New Approach to clustering”, Information and Control, 15, pp. 22-32, 1969. |
| [16] | P. Scheunders, “A Genetic C-Means Clustering Algorithm Applied to Color Image Quantization”, Pattern Recognition, vol. 30, no. 6, pp. 859-866, 1997. |
| [17] | Y. Wang, “Fuzzy clustering analysis by using genetic algorithm”, ICIC Express Letters vol. 2, no. 4, December 2008. |
| [18] | K. L. Wu and M. S. Yang, “A cluster validity index for fuzzy clustering”, Pattern Recognition Letters, vol. 26, pp. 1275-1291, 2005. |
| [19] | K. L. Wu, M. S. Yang and J. N. Hsieh “Robust cluster validity indexes”, Pattern Recognition, vol. 42, Issue 11, pp. 2541-2550, 2009 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML