-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
2012; 2(4): 70-75
doi: 10.5923/j.ajsp.20120204.03
Improving LMS/NLMS-Based Beamforming Using Shirvani-Akbari Array
Shahriar Shirvani Moghaddam 1, Farida Akbari 2
1Digital Communications Signal Processing (DCSP) Research Lab., Faculty of Electrical and Computer Engineering, Shahid Rajaee Teacher Training University (SRTTU), Lavizan, 16788-15811, Tehran, Iran
2Electrical Engineering Department, Tehran South Branch, Islamic Azad University, Tehran, Iran
Correspondence to: Shahriar Shirvani Moghaddam , Digital Communications Signal Processing (DCSP) Research Lab., Faculty of Electrical and Computer Engineering, Shahid Rajaee Teacher Training University (SRTTU), Lavizan, 16788-15811, Tehran, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
ULA is the most common geometry exploited in array signal processing. In the beamforming operation, employing the ULA leads to obtaining narrower beamwidth with respect to other geometries in similar element numbers. Recently, Shirvani and Akbari proposed a new array by adding two elements to the ULA in top and bottom of the array axis, named as SAA. This new array offers a considerable improvement in DOA estimation performance in detection and resolution of signal sources placed at angles close to the array endfires. In this article, the performance of the proposed SAA is investigated especially in beamforming and compared with ULA. LMS and NLMS algorithms that are popular adaptive beamforming methods are used for evaluation and comparing the performance of SAA and ULA. Considering array factor, mean square error and bit error rate metrics, simulation results show improved convergence speed and higher data transmission accuracy in different signal source locations, boresight angles as well as endfire ones, for SAA with respect to ULA.
Keywords: Uniform Linear Array, Shirvani-akbari array, Beamforming, LMS, NLMS
Article Outline
1. Introduction
- Beamforming using an antenna array is a promising and necessary task in the next generation wireless and mobile systems. Sensor arrays are extensively used in signal processing and their capability has made numerous applications in different fields such as radar, sonar, radio astronomy, medical diagnosis, acoustics and mobile or wireless communications. Combination of the signals collected from array sensors provides temporal and spatial analysis of wave-fields and yields directional sensitivity for the system. The important tasks considered in array signal processing are beamforming, Angle Of Arrival (AOA) or Direction Of Arrival (DOA) estimation and source tracking. Variant techniques and algorithms are available with different characteristics in efficiency, accuracy and computational costs and also numerous studies are attempting to improve these techniques or proposing new efficient methods[1, 2]. In addition to different algorithms, structure of array plays a key role in array signal processing. Various arrangements are studied and have demonstrated significant effects on the performance of the system.Uniform Linear Array (ULA) is the most common configuration used for array processing investigations. This geometry is simple in analysis and implementation and provides a good accuracy via formation of narrow beams during beamforming. However, ULA can analyse the surrounding wave-fields in a particular dimension and provides one-Dimensional (1-D) coverage. Furthermore, ULA cannot give a uniform performance in all directions. DOA estimation and beamforming with ULA leads to weak results at the angles close to the array endfires. Therefore, other array geometries are investigated to obtain a uniform performance. Uniform Circular Array (UCA) is another common geometry used for array processing. This structure has further complexity in implementation as well as analysis with respect to ULA. Instead, UCA can provide 2-D coverage and present uniform performance in all directions. Beams in UCA are wider than ULA and this affects resolution of the array[3, 4]. Concentric Circular Array (CCA) or multi-ring arrays are other configurations that provide more flexibility in size and width of the obtained beams[5]. However, the required computational complexity for analysing the array structure increases in CCAs. Planar arrays are also used for 2-D and more precise beam-pattern generation. 3-D arrays and conformal arrays may be used in particular applications to provide M-D performance and conformity with the vehicle or system they are integrated with it[3]. However, these structures are complicated in calculations as well as implementation and research works are attending to find and develop simple arrangements which present better efficiency and perform uniform in all directions. Combination of linear arrays is considered in literature and has shown improvements in array performance specially the accuracy of DOA estimation algorithms. Some of these structures are parallel linear arrays and Displaced Sensor Arrays (DSAs), L-shaped and two L-shaped arrays, V-shaped, Y-shaped, Uniform Rectangular Arrays (URA), hexagonal arrays and so on[6-11]. Each configuration has particular properties and capabilities. These geometries are often used for DOA estimation and they can provide at least 2-D DOA estimation capability. In Ref.[11] different types of array structures (ULA, UCA and URA) for smart antennas, DOA estimation and beamforming have been examined. This paper is following the authors’ earlier papers[12-14], in which a simple ULA-based geometry was introduced that could provide a significant improvement in DOA estimation capability and resolution threshold in border angles of the array endfire. In this article, by focusing on antenna beamforming, the capability of Shirvani-Akbari Array (SAA) which adds two elements to the ULA in top and bottom of the array axis is investigated. Two well-known adaptive beamforming techniques, Least Mean Squares (LMS) and Normalized Least Mean Squares (NLMS) are exploited for evaluation of SAA performance. Simulation results are compared with the results of beamforming using conventional ULA. Numerical results show higher accuracy and also uniform performance through this new proposed array with respect to conventional ULA.The rest of paper is organized as follows. Section 2 describes signal model for array processing through ULA as well as SAA. A brief overview of adaptive beamforming techniques and description of LMS and NLMS algorithms are stated in sections 3, 4, respectively. In section 5, simulation results using MATLAB software are presented and the performance of both arrays is compared together. Finally, conclusion remarks are given in section 6.
2. Signal Model for Array Processing
- Fig. 1 depicts the block diagram of an adaptive array system. System is composed of an array of sensors, complex weights, summer and a signal processing unit.
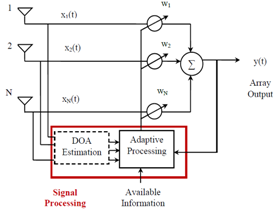 | Figure 1. Block diagram of an adaptive array system |
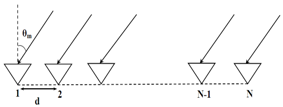 | Figure 2. ULA geometry |
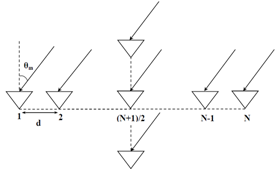 | Figure 3. SAA geometry |
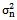 . The incident signals are assumed to be direct Line Of Sight (LOS) and uncorrelated with the noise. The input signal vector denoted by
. The incident signals are assumed to be direct Line Of Sight (LOS) and uncorrelated with the noise. The input signal vector denoted by 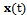 can be written as (1).
can be written as (1).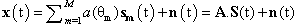 | (1) |
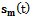 is
is 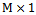 vector concerning to the m-th source located at direction
vector concerning to the m-th source located at direction 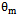 from the array boresight.
from the array boresight. 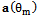 is the
is the 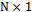 steering vector or response vector of the array for direction of
steering vector or response vector of the array for direction of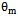 . For ULA, the steering vector is as:
. For ULA, the steering vector is as: | (2) |
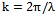 . For SAA, the steering vector has
. For SAA, the steering vector has 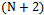 element as (3). The first N rows of
element as (3). The first N rows of 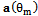 for SAA are equivalent with steering vector of ULA. By addition of two remained rows with respect to ULA,
for SAA are equivalent with steering vector of ULA. By addition of two remained rows with respect to ULA, 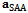 is expressed as:
is expressed as: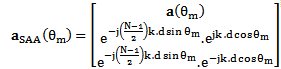 | (3) |
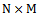 matrix of steering vectors, written as:
matrix of steering vectors, written as: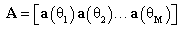 | (4) |
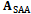 with
with 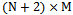 dimensions is defined as:
dimensions is defined as: | (5) |
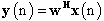 | (6) |
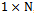 ,
,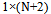 weight vector for ULA and SAA. H denotes the Hermitian, conjugate transpose, operator and x is the received signal vector defined in (1).
weight vector for ULA and SAA. H denotes the Hermitian, conjugate transpose, operator and x is the received signal vector defined in (1). 3. Adaptive Array Beamforming
- Beamforming that is also referred as spatial filtering is the process of adjusting the antenna radiation pattern so that the antenna focuses energy towards Signal Of Interest (SOI) and nulls directed to Signals Not Of Interest (SNOIs). This task can be fulfilled through different approaches. Although some earlier techniques such as classical beamforming or fixed-beam methods carry out this process with lower complexity, adaptive beamforming techniques are more capable. These methods adjust array weights dynamically with respect to signal environment and perform interference mitigation as well as desired signal tracking. Therefore, adaptive beamforming methods have been more considerable in recent years. In an overview, adaptive algorithms are classified in two categories: non-blind and blind algorithms. Adaptive beamforming techniques generally need some initial information about the signal characteristics to obtain an appropriate performance. This initial information is provided via a reference signal, DOA estimation methods or some particular properties of the desired signal. The beamforming methods that utilize a reference signal, known as training sequence, are called training-based or non-blind algorithms. LMS and its variants, Recursive Least Squares (RLS) and Sample Matrix Inversion (SMI) are training-based algorithms. Blind algorithms use the desired signal properties and their DOA instead of training sequences to determine the weight vector. Constant Modulus Algorithm (CMA), Decision Directed (DD), Conjugate Gradient (CG), Least Squares (LS) and Spectral self-Coherence REstoral (SCORE) are some examples of blind algorithms[2]. In this research, two popular and reliable non blind methods, LMS and NLMS are discussed and simulated in both ULA and SAA.
4. LMS and NLMS Description
- LMS is an adaptation technique based on the steepest-descent method. The algorithm updates the weights recursively by estimating gradient of the error surface and changing the weights in the direction opposite to the gradient to minimize the Mean Square Error (MSE)[2,15]. Error signal is the difference between desired signal,
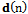 , and array output,
, and array output, 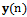 , computed by the expression:
, computed by the expression: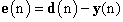 | (7) |
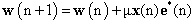 | (8) |
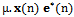 applied to the weight vector during LMS algorithm, is proportional to the input vector
applied to the weight vector during LMS algorithm, is proportional to the input vector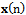 . Therefore, a gradient noise amplification problem occurs in the standard LMS algorithm. This problem can be solved by normalized LMS, in which a data dependent step size is used for adaptation. NLMS normalizes the weight vector correction term with respect to the squared Euclidean norm of the input vector
. Therefore, a gradient noise amplification problem occurs in the standard LMS algorithm. This problem can be solved by normalized LMS, in which a data dependent step size is used for adaptation. NLMS normalizes the weight vector correction term with respect to the squared Euclidean norm of the input vector 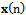 at time n. So its equation can be written as:
at time n. So its equation can be written as: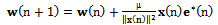 | (9) |
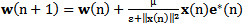 | (10) |
 -NLMS algorithms are employed but new proposed SAA configuration can be applied for all above mentioned versions of LMS.
-NLMS algorithms are employed but new proposed SAA configuration can be applied for all above mentioned versions of LMS.5. Numerical Results
- For simulation of LMS and NLMS in ULA and SAA, two arrays with 7 and 9 elements and half wavelength inter-element spacing are assumed. The performance of beamforming algorithms is evaluated in both arrays and in different signal source locations using MATLAB. Beamforming performance may be evaluated with different criteria. In this investigation, absolute value of Array Factor (AF), MSE, and Bit Error Rate (BER) are considered as performance metrics.Fig. 4 depicts the radiation pattern when the desired signal is located at
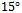 and two interference signals are assumed to be located at
and two interference signals are assumed to be located at 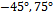 and the Signal to Noise Ratio (SNR) and Signal to Interference Ratio (SIR) are assumed to be 10 dB and 3 dB, respectively. Both arrays have tracked desired signal successfully and placed appropriate nulls in the interferers' directions. Beamwidth in SAA is a little wider than ULA in middle angles.
and the Signal to Noise Ratio (SNR) and Signal to Interference Ratio (SIR) are assumed to be 10 dB and 3 dB, respectively. Both arrays have tracked desired signal successfully and placed appropriate nulls in the interferers' directions. Beamwidth in SAA is a little wider than ULA in middle angles.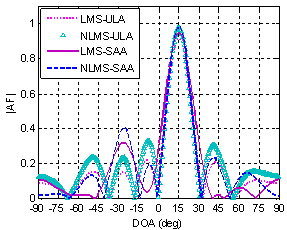 | Figure 4. Array factor for the middle DOAs |
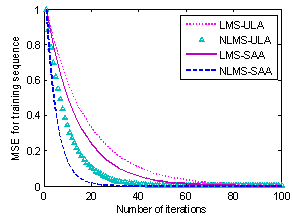 | Figurea 5. MSE of training sequence for the middle DOAs |
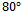 and two interference signals are assumed at
and two interference signals are assumed at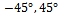 . Radiation pattern of both ULA and SAA arrays is shown in Fig. 7. Main lobes that are formed at border angles have better tracking accuracy at desired DOA and their widths are less than main beams formed in these directions by ULA.
. Radiation pattern of both ULA and SAA arrays is shown in Fig. 7. Main lobes that are formed at border angles have better tracking accuracy at desired DOA and their widths are less than main beams formed in these directions by ULA. 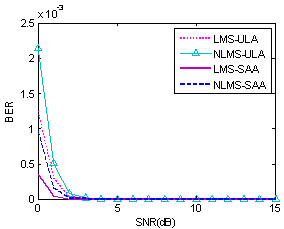 | Figure 6. BER versus SNR for the middle DOAs |
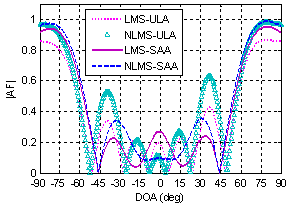 | Figure 7. Array factor for the border DOAs |
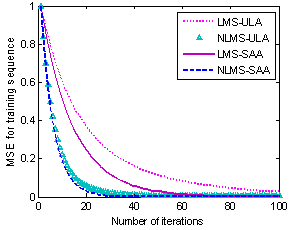 | Figure 8. MSE of training sequence for the border DOAs |
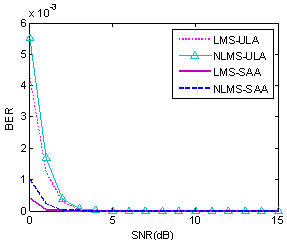 | Figure 9. BER versus SNR for the border DOAs |
6. Conclusions
- In this paper, the performance of a new proposed array, SAA, for adaptive beamforming task was investigated. The new array is based on ULA configuration with two extra elements at the top and bottom of the array axis. Two popular training-based beamforming algorithms, LMS and NLMS were considered for this purpose. Nevertheless, the performance of SAA and ULA is the same for the antenna beamforming in the case of source and interferers located at middle angles, SAA offers a well performance in detecting and resolving sources located at array endfires. Simulation results show improved convergence speed and accuracy in data transmission considering AF, MSE and BER performance metrics for the new array, especially for low SNRs. This research focused on LMS and NLMS algorithms for both ULA and SAA, but the similar procedure can be applied for other beamforming algorithms.
ACKNOWLEDGEMENTS
- This work was supported by Shahid Rajaee Teacher Training University (SRTTU) under contract number 720 (20.1.1391).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML