F. Souibgui, F. BenHmida, A. Chaari
Department of Electrical Engineering, Higher School of Sciences and Techniques of Tunis, University of Tunis, 5 Street Taha Hussein, B.P. 56-1008 Tunis, Tunisia
Correspondence to: F. Souibgui, Department of Electrical Engineering, Higher School of Sciences and Techniques of Tunis, University of Tunis, 5 Street Taha Hussein, B.P. 56-1008 Tunis, Tunisia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper introduces the particle-filtering (PF) based framework for fault diagnosis in non-linear systems and noise and disturbances being Gaussian. In this paper, we use the sequential Monte Carlo filtering approach where the complete posterior distributions of the estimates are represented through samples or particles as opposed to the mean and covariance of an approximated Gaussian distribution. We compare the fault detection performance with that using the extended Kalman filtering and investigate the isolation performance on a nonlinear system.
Keywords:
Recursive Bayesian approach, Extended Kalman filter, particle filter, Parameter estimation, fault detection
1. Introduction
Problem of fault detection and isolation (FDI) in dynamic systems has received considerable attention for many years due to icreasingly complex systems and reliability[2]. Different types of approaches appearing in literature, as can be seen from a large number of survey papers[1-6]. The problem of fault detection can be roughly divided into two major categories: First, we need to estimate the unknown and un measurable state variable of model and generate residuals on the basis of the available observations and a model of the system. Secondly, we need to decide on the occurrence of a fault based on the residuals generated[2]. For the stochastic systems, much of development in fault detection schemes has relied on the system being linear and disturbances being Gaussian. In such cases, the Kalman filter (KF) is known to be optimal and employed for state estimation. The innovations errors from the KF are used as the residuals, based on which statistical hypothesis tests are carried out for fault detection (see e.g. willsky,[4] and Darouach et al.,[5]). However, in comparison with linear systems, the literature addressing fault detection (FD) for nonlinear stochastic systems is not simple, the main reason being that the estimation of the state vector of a nonlinear stochastic system is not easy. Suboptimal solutions use some form of approximation for non linear systems will additive Gaussian noise and disturbance by employing lineraisation techniques[9]. In this case, Kalman filter is usually replaced by the extended Kalman filter (EKF) as a residual generator. However, EKF is only an approximation method for non linear filtering; there are no general results to guarantee that such approximation will work in most case. When the nonlinearity system is strong and non-Gaussian distributions, the performance of EKF will descend or even become divergent[9,10,13]. For that the fault detection for nonlinear stochastic systems is known as a difficult problem and very few results are available[8,15]. General solution of the state estimation problem is described by the Bayesian recursive relations. The closed form solution of the Bayesian recursive relations is available for a few special cases (Gaussian or non- Gaussian). During the1990s, the particle filter (PF) which dominated in recursive nonlinear state estimation, has attracted much attention and has been widely applied in many fields (see e.g (Gordon and al.[7], Bolviken and al.[8], Doucet and al.[10], Benhmida and al.[9]). The PF solves the Bayesian recursive relations using Sequential Monte Carlo (SMC) methods. These methods allow for a complete representation of the posteriori probability density function of the states, so that any statistical estimates, such as the Minimum Mean Squared Error estimate (MMSE) and the Maximum a Posteriori Probabilities (MAP) can by easily computed. In year 2000 Kadirkamanathan and al.[2] introduced Sequential Monte Carlo methods into field of fault detection and isolation(FDI). Different types of approaches appearing in literature of FDI problem[1,3] for solving general nonlinear systems with known sets of possible faults. In this latter, the particle filter is combined with the innovation based fault detection techniques to develop a fault detection and isolation scheme. The paper is organized as follows: section 2 states the problem of interest. In section 3 we treat the Recursive Bayesian approach. An Innovation-based fault detection of the stochastic system and detected to update step of the Extended Kalman Filter in section4. The particle filter based detection and isolation schemes are described in sections5, 6 and7. Finally, we illustrate in section 8 the simulation results on a highly non linear system witch demonstrate the effectiveness of the particle Filter.
2. Problem Formulation
The problem of fault detection and isolation (FDI) consist of making the decision on the presence or absence of faults in the motored system. In this paper, the dynamics of the system considered is assumed known and given by discrete time nonlinear stochastic system given by the state equation (1) and the measurement equation (2):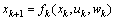 | (1) |
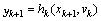 | (2) |
where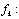
 is a possibly nonlinear function defining the state at time
is a possibly nonlinear function defining the state at time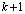 from the previous state at timek,
from the previous state at timek,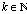 and
and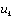 is the known input. The function
is the known input. The function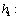
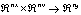 is a possibly nonlinear function defining the relation between state, parameter and the measurement at time k.
is a possibly nonlinear function defining the relation between state, parameter and the measurement at time k. 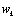 and
and 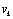 the uncorrelated white noise sequences of zero-mean and covariance matrices
the uncorrelated white noise sequences of zero-mean and covariance matrices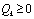 and
and 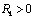 , respectively. The initial state is uncorrelated with the white noises processes
, respectively. The initial state is uncorrelated with the white noises processes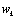 and
and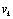 and
and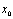 is a Gaussian random variable with
is a Gaussian random variable with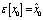 and
and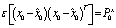 where
where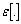 denotes the expectation operator. We denote by
denotes the expectation operator. We denote by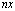 ,
,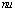 ,
,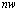 ,
, 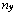 and
and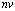 respectively, the dimensions of the state, the input vectors, process noise vectors, the measurement and measurement noise vectors. Let
respectively, the dimensions of the state, the input vectors, process noise vectors, the measurement and measurement noise vectors. Let 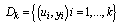 denote the available measurement information at the time k :The type of faults of interest here are the failure type where the system parameter values to in new value reflected in a change in the state transition function
denote the available measurement information at the time k :The type of faults of interest here are the failure type where the system parameter values to in new value reflected in a change in the state transition function 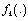 at time k and the measurement function
at time k and the measurement function 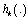 at time k such fault can be detected using the state observer approach.
at time k such fault can be detected using the state observer approach.
3. Recursive Bayesian Approach
This section gives a brief informal introduction to the basic recursive Bayesian approach. Recursive Bayesian state estimation of discrete-time nonlinear stochastic systems has been the subject of a considerable research interest over the last three decades. Two good surveys on nonlinear recursive estimation are provided by (Sorenson, 1988[11]) and (Kulhavsy, 1996[12]). Another good reference for nonlinear recursive and non recursive estimation is (Jazwinski, 1970[13]). The idea of the Bayesian approach to state estimation problems involve the construction of the probability density function of the current state 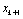 , based on the input output data D observed up to instant k+, more precisely, to estimate the conditional probability density function
, based on the input output data D observed up to instant k+, more precisely, to estimate the conditional probability density function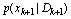 . In general, no accurate tow estimator exists, the Minimum Mean Squared Error estimate (MMSE) and the Maximum a Posteriori Probabilities (MAP) estimate for nonlinear stochastic systems, even if the noises are assumed to be Gaussian or non-Gaussian as follows
. In general, no accurate tow estimator exists, the Minimum Mean Squared Error estimate (MMSE) and the Maximum a Posteriori Probabilities (MAP) estimate for nonlinear stochastic systems, even if the noises are assumed to be Gaussian or non-Gaussian as follows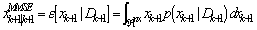 | (3) |
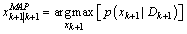 | (4) |
From a Bayesian perspective, the propagation of the posteriori 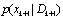 of
of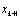 based on the observation sequence
based on the observation sequence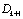 , can be basically achieved by performing three recursive steps. It can be expressed as followsStep (1). Initialization:
, can be basically achieved by performing three recursive steps. It can be expressed as followsStep (1). Initialization: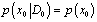 | (5) |
Step (2). Chapman-Kolmogorov equation: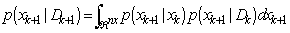 | (6) |
Step (3). Bayes theorem update:According to the Bayes theorem the posterior probability density follows from the relation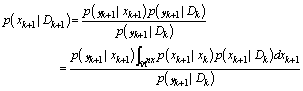 | (7) |
where the 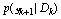 the normalizing constant
the normalizing constant 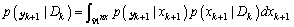 | (8) |
from the equations (6) and (8), we obtain the equation (7)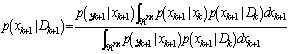 | (9) |
Step (4). k  k + 1, go to Step (2).In steps (2) and (3)
k + 1, go to Step (2).In steps (2) and (3) 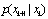 is defined by the state function, Eq. 1 and
is defined by the state function, Eq. 1 and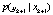 is the conditional density of observation, given the state at time k+1, Eq. 2. Similarly the posterior probability density for smoothing
is the conditional density of observation, given the state at time k+1, Eq. 2. Similarly the posterior probability density for smoothing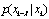
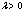 and filtering,
and filtering,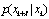 ,
, 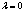 can be defined.However this paper is only concerned with prediction, and thus the only situation of interest is where
can be defined.However this paper is only concerned with prediction, and thus the only situation of interest is where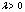 . The posteriori probability density given by the above steps is exact, but in general, it can be viewed as an infinite dimensional system, thus not implementable. There is however a severe problem in Baysian state estimation for nonlinear systems that makes is difficult to readily the equations (6) and (7) because they involve high dimensional integrations. The most important special case is when the system is linear, i.e,
. The posteriori probability density given by the above steps is exact, but in general, it can be viewed as an infinite dimensional system, thus not implementable. There is however a severe problem in Baysian state estimation for nonlinear systems that makes is difficult to readily the equations (6) and (7) because they involve high dimensional integrations. The most important special case is when the system is linear, i.e, 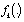 and
and 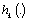 are linear and one assumes that the noise and the initial state are Gaussian,i.e.,
are linear and one assumes that the noise and the initial state are Gaussian,i.e.,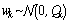
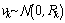 . The solution is provided by the Kalman filter. More details and background for this filter can be found in[13]. We also describe how, when the analytic solution is intractable, Extended Kalman filter, and Particle filter approximate the optimal Bayesian solution.
. The solution is provided by the Kalman filter. More details and background for this filter can be found in[13]. We also describe how, when the analytic solution is intractable, Extended Kalman filter, and Particle filter approximate the optimal Bayesian solution.
4. Innovation-Based FDI Design
One of the main difficulties in fault detection of the stochastic system described by(1) and(2) is due to the presence of unknown and unmeasured state variables x. The idea is to generate estimates of the states and the predicted outputs.The residuals or innovation from the output prediction are used in a measure which changes significantly under a failure type fault. For nonlinear Gaussian system, the states are estimated using a extended Kalman filter[13], an approximate sub-optimal estimate probability density functions described in section3, obtained by linearisation, is recursively given according to be Gaussian,i.e.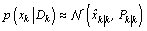 | (10) |
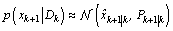 | (11) |
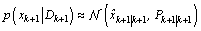 | (12) |
where the states and matrix covariance are estimated according to the following equations:Prediction: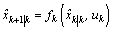 | (13) |
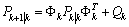 | (14) |
Correction: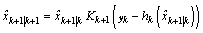 | (15) |
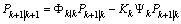 | (17) |
Where 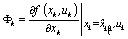
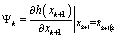 The residual or the innovation is then,
The residual or the innovation is then,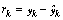 | (18) |
where the predicted output based on the EKF state estimate is given by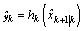 | (19) |
It is well-known that, under fault free or normal operation, the innovations are zero mean Gaussian with covariance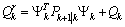 | (20) |
Any faults or changes in system dynamics can therefore be detected by a change in the Weighted Squared Residual (WSR) measure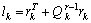 | (21) |
This however can lead to false alarms occurring at a particular instant due to disturbances and noise and a more robust decision function for fault detection is the weighted sum squared residual (WSSR) (see e.g.[4]) defined as follows: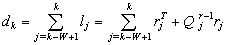 | (22) |
where W is the length of the sliding window within which the residual measure is summed. The window length W should be chosen in accordance with the requirement for detection time and the fault alarm is set at time k when the condition[4]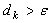 | (22) |
is satisfied, 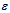 being the threshold. When using extended kalman filter to estimate the states and hence
being the threshold. When using extended kalman filter to estimate the states and hence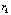
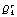 . The measure Lk will thus consist of fluctuations which can in turn lead to higher false alarm rates and also to faults not being detected.
. The measure Lk will thus consist of fluctuations which can in turn lead to higher false alarm rates and also to faults not being detected.
5. Particle filtering (PF)
We have so far presented two filtering methods that rely on Gaussian approximation. In this section, we shall present the particle filter (PF), based on a Monte-Carlo technique, which was first proposed by Gordon (Gordon et al., 1993). Thereafter, a number of alternative PF algorithms have been proposed. The PF uses sequential Monte-Carlo methods to approximate the optimal filtering by representing the probability density function (pdf) with a swarm of particles. Because the PF is able to handle any functional nonlinearity and system or measurement noise of any probability distribution, it has attracted much attention in the nonlinear non-Gaussian state estimation field (Bolviken et al.,[8]; Doucet et al.,[10]).The objective is to recursively construct the posterior pdf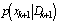 of the state, given the measured output
of the state, given the measured output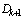 and assuming conditional independence of the measurement sequence, given the states. The PF works in two stages: 1) The prediction stage uses the state-transition model in(1) to predict the state pdf one step ahead. The pdf obtained is called the prior.2) The update stage uses the latest measurement to correct the prior via the Bayes rule. Particle filters represent the pdf by N random samples (particles)
and assuming conditional independence of the measurement sequence, given the states. The PF works in two stages: 1) The prediction stage uses the state-transition model in(1) to predict the state pdf one step ahead. The pdf obtained is called the prior.2) The update stage uses the latest measurement to correct the prior via the Bayes rule. Particle filters represent the pdf by N random samples (particles) 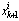 with their associated weights
with their associated weights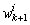 , normalized so that
, normalized so that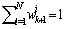 . At time instant k, the prior pdf
. At time instant k, the prior pdf 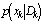 is represented by N samples
is represented by N samples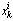 and the corresponding weights
and the corresponding weights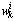 . To approximate the posterior
. To approximate the posterior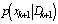 , new samples
, new samples 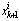 and weights
and weights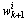 are generated.Samples
are generated.Samples 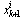 are drawn from a (chosen) importance density function
are drawn from a (chosen) importance density function 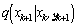 , and the weights are updated, using the current measurement
, and the weights are updated, using the current measurement 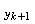
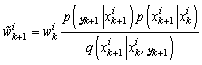 | (23) |
and normalized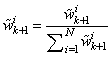 The posterior pdf is represented by the set of weight samples, conventionally denoted by:
The posterior pdf is represented by the set of weight samples, conventionally denoted by: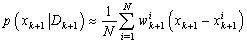 | (24) |
Here, we choose the importance density 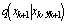 equal to the state-transition pdf
equal to the state-transition pdf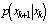 . The weight update equation (23) then becomes:
. The weight update equation (23) then becomes: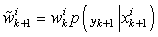 | (25) |
A common problem of PF is the particle degeneracy: after several iterations, all but one particle will have negligible weights. Therefore, particles must be resampled. A standard measure of the degeneracy is the effective sample size: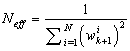 Thus, the degeneracy phenomenon can be detected when Neff < Nthr where Nthr is the threshold value Nthr
Thus, the degeneracy phenomenon can be detected when Neff < Nthr where Nthr is the threshold value Nthr 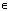 [1, N]. When such condition is encountered, the resampling algorithm is just applied. For more details on particle filters, refer to[3,10,15].
[1, N]. When such condition is encountered, the resampling algorithm is just applied. For more details on particle filters, refer to[3,10,15].
6. Particle Filter for Fault Detection
For the purpose of fault detection, the method proposed in this paper is to design several particle filters, each assuming a different subset of the possible faults formulated in system described by (1) and (2). The advantages of using the complete probability density function of the system state in fault detection is bound to be superior to one which uses approximations, such as in the extended kalman filter (EKF). Our approach is precisely to replace the EKF based estimation scheme by the particle filter, and the weighted squared residual (WSSR) measure by an appropriate innovations likelihood measure as the fault detection criteria[1,3]. The following algorithm describes the complete particle filter based fault detection scheme:Particle filter based fault detection Algorithm• Step 1: State predictionSamples 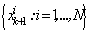 are generated as particle filter prediction step.• Step 2: Output predictionThe output prediction samples
are generated as particle filter prediction step.• Step 2: Output predictionThe output prediction samples 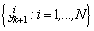 are generated using the measurement equation in (2), where,
are generated using the measurement equation in (2), where,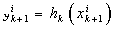 • Step 3: Residual generationSample mean of the predicted measurements is computed as,
• Step 3: Residual generationSample mean of the predicted measurements is computed as, 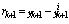 • Step 4: Fault detectionCompute the likelihood is given by,
• Step 4: Fault detectionCompute the likelihood is given by,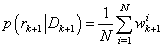 The windowed likelihood is
The windowed likelihood is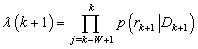 Or equivalently the negative log likelihood is
Or equivalently the negative log likelihood is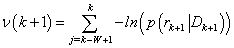 is computed and the condition
is computed and the condition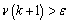 is tested for the presence of fault.
is tested for the presence of fault.
7. Augmented States Model for Fault Isolation
In the previous section is a fault detection scheme which cannot readily be extended to fault isolation. The idea is to view the parameters as additional states. Using the state augmentation technique, a new state vector can be defined: 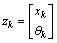 Here
Here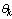 is the unknown fault parameter vector to be estimated. Because
is the unknown fault parameter vector to be estimated. Because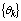 is not ergodic,
is not ergodic, 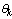 cannot be tracked in the PF algorithm. Therefore, in order to track the dynamics of
cannot be tracked in the PF algorithm. Therefore, in order to track the dynamics of 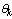 an artificial dynamic noise vector is added to the model of the unknown parameter
an artificial dynamic noise vector is added to the model of the unknown parameter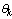 :
: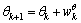 | (26) |
where 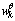 is the parameter noise. Then the augmented system and measurement functions are respectively defined as
is the parameter noise. Then the augmented system and measurement functions are respectively defined as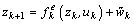 | (27) |
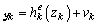 | (28) |
where 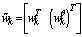 . Because
. Because  is artificial, its statistical properties need to be determined. In this paper, we assume that
is artificial, its statistical properties need to be determined. In this paper, we assume that  is a zero-mean Gaussian white noise process that is introduced for parameter evolution to allow the exploration of the parameter space. Given the above system representation (27) and (28), the particle filter outlined in this setion5, can be used to obtain the sample-based joint probability function density of the state x and parameter vector
is a zero-mean Gaussian white noise process that is introduced for parameter evolution to allow the exploration of the parameter space. Given the above system representation (27) and (28), the particle filter outlined in this setion5, can be used to obtain the sample-based joint probability function density of the state x and parameter vector such an estimate based on particle filter algorithm is given by,
such an estimate based on particle filter algorithm is given by,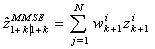 | (29) |
The estimate is essentially a weighted average of the particles representing the underlying distribution[6,8]. The parameter estimate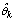 can be compared to the nominal values
can be compared to the nominal values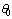 as a means for fault detection and its deviation
as a means for fault detection and its deviation 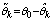 .
.
8. Numerical Example
An example is presented in this section to illustrate the operation of the particle filter based fault detection and isolation proposed in this paper. The considered system is described by following the dynamical equations,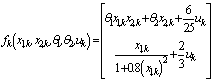 | (30) |
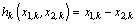 | (31) |
The initial joint state vector, 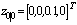 ,
,  . The measurement and process noise signals are both set to be Gaussian with covariance matrices,
. The measurement and process noise signals are both set to be Gaussian with covariance matrices,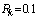
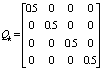 ,The input and observation shown in Fig.1. The time index is incremented as k=0,…….,200. The nominal values of the parameters are
,The input and observation shown in Fig.1. The time index is incremented as k=0,…….,200. The nominal values of the parameters are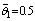 and
and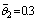 . In the simulation, the length of the data window for WSSR calculation is N1=30 and the number of particles in the particle filter is N = 600. The fault is simulated to occur at time k= 100 at which time the parameter
. In the simulation, the length of the data window for WSSR calculation is N1=30 and the number of particles in the particle filter is N = 600. The fault is simulated to occur at time k= 100 at which time the parameter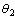 jumps from a value of
jumps from a value of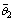 to
to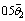 while
while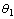 remains unchanged. The Weighted Sum Squared Residual (WSSR) results for the EKF is shown in Figure 2 and the negative log likelihood for the particle filter in Figure 3. The EKF based approach fails to detect the occurrence of the fault around k =100 as evidenced by Figure 2 where there is no significant change in WSSR. The detection performance is unacceptable. On the other hand, the particle filter detects the fault at k =104 a threshold value of
remains unchanged. The Weighted Sum Squared Residual (WSSR) results for the EKF is shown in Figure 2 and the negative log likelihood for the particle filter in Figure 3. The EKF based approach fails to detect the occurrence of the fault around k =100 as evidenced by Figure 2 where there is no significant change in WSSR. The detection performance is unacceptable. On the other hand, the particle filter detects the fault at k =104 a threshold value of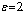 . The change in log likelihood is quite pronounced following the onset of the fault. The combined fault detection isolation (FDI) scheme proposed in section7was also applied to the above example.
. The change in log likelihood is quite pronounced following the onset of the fault. The combined fault detection isolation (FDI) scheme proposed in section7was also applied to the above example.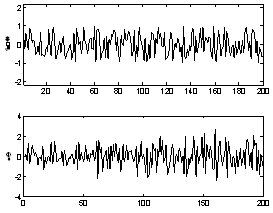 | Figure 1. The input uk and observationyk |
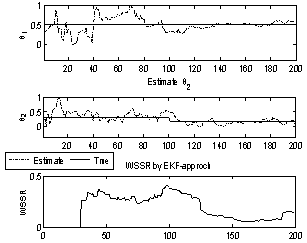 | Figure 2. (a) Parameter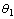 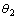 estimates from the EKF and true values, (b) weight sum squared residual (WSSR) -EKF estimates from the EKF and true values, (b) weight sum squared residual (WSSR) -EKF |
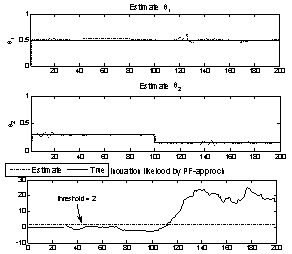 | Figure 3. (a) Parameter  estimates from the ParticleFilter and true values, (b )Negative log likelihood - Particle Filter estimates from the ParticleFilter and true values, (b )Negative log likelihood - Particle Filter |
Figure 5 shows that the change in the parameter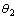 is tracked following an initial transient and the estimate for the other parameter
is tracked following an initial transient and the estimate for the other parameter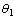 hovers around the nominal parameter. The PF successfully tracks the system parameter, while this is not seen for EKF (Figure3). Thus we can safely conclude that the fault in the system is due to the change in the parameter
hovers around the nominal parameter. The PF successfully tracks the system parameter, while this is not seen for EKF (Figure3). Thus we can safely conclude that the fault in the system is due to the change in the parameter 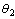
9. Conclusions
This paper, considers the Particle filter based approach to fault detection and isolation scheme developed. This approach is applicable to general non-linear systems with Gaussian or non Gaussain disturbance noise. The fault detection performance compared with that using the EKF. The results from simulation show that the detectability of the particle filtering approach is superior to the EKF based scheme, especially in the case where the system model is highly nonlinear. The fault isolation scheme is also shown to identify the parameter associated with the fault and the level of the fault.
References
| [1] | D. H. Zhou, Y. G. Xi and Z. J. Zhang Nonlinear adaptive fault detection filter” in Int. J. Systems Sci.,2563- 2571, 1991. |
| [2] | Kadirkamanathan, V., P. Li, M.H. Jaward, and S.G. Fabri. Particle filtering-based fault detection in nonlinear stochastic systems. International Journal of Systems Science (33), 259265, 2002. |
| [3] | R. Isermann. Process fault detection based on modeling and estimation methods - A survey. Automatica, 20: 387-404, 1984. |
| [4] | A. S. Willsky, A survey of design methods for failure detection in dynamic systems Automatica, 12:601- 611, 1976. |
| [5] | M. Darouach, M.Zasadziski, A.B.OnanaandS, Kalman filtering with unknown inputs via optimal state estimation of singular systems.In Int.J.systems science, 26,2015-2028,1995 |
| [6] | J.Y.Keller,L.Summerer,M.BoutayebandM.Darouach,Generalized likelihood ratio approch for fault detection in linear dynamic stochastic systems with unknown inputs, in Int.J.systems science, 27, 1231-1241. |
| [7] | N. J.Gordon, D. J. Salmond and A. F. M. Smith, Novel approach to nonlinear/non-Gaussian Bayesian state estimation , IEE Proceedings-F, 140(2): 107- 113,1993. |
| [8] | E.Bolviken, P. J. Acklam, N.Christophersen, and J-M.Stordal, Monte Carlo filters for non-linear state estimation, automatic, 37(2): 177-183, 2001. |
| [9] | F. Ben Hmida, F. Souibgui and A. Chaari, Estimationd’tat des stochastiques non linaires par l’approche baysienne recursive, 8th confrence international STA07, 05-07novembre a Monastir-TUNISIE, 2007. |
| [10] | A.Doucet, N.Freitas, and N.Gordon, SequentialMonte Carlo Methods in Practice Springer-Verlag, New York, 2001. |
| [11] | R.Kulhavsy, Recursive Nonlinear Estimation A GeometricApproach. Lecture Notes in Control and Information Sciences 216. Springer-Verlag, London,1996. |
| [12] | H.Sorenson, Recursive estimation for nonliear dynamic systems. In Spall, J., editor, Bayesian Analysisof Time Series and Dynamic Models, pages 127-165. Marcel Dekker inc., New York, 1988. |
| [13] | A.Jazwinski, Stochastic processes and filtering theory. Mathematics in science and engineering. Academic Press, New York, 1970. |
| [14] | F. Ben Hmida, F. Moussa, F. Souibgui, and A. Chaari, Estimation jointe etat-paramtres des systmes stochastiques non linaires par l’approche baysienne recursive, 5th Confrence Internationale d’Electrotechnique et d’Automatique, 02-04 Mai a Hammamet TUNISIE, 2008. |
| [15] | F. Souibgui, F. Ben Hmida, and A.Chaari, Sequential Bayesian State Estimation of Nonlinear, Non-Stationary and Non-Gaussian Stochastic System Technique Based on Bootstrap filter, 9th conference international STA09, 05-07 November a Hammamet TUNISIE,2009 |

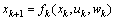
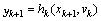
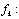
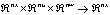 is a possibly nonlinear function defining the state at time
is a possibly nonlinear function defining the state at time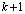 from the previous state at timek,
from the previous state at timek,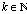 and
and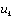 is the known input. The function
is the known input. The function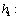
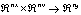 is a possibly nonlinear function defining the relation between state, parameter and the measurement at time k.
is a possibly nonlinear function defining the relation between state, parameter and the measurement at time k. 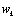 and
and 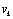 the uncorrelated white noise sequences of zero-mean and covariance matrices
the uncorrelated white noise sequences of zero-mean and covariance matrices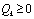 and
and 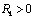 , respectively. The initial state is uncorrelated with the white noises processes
, respectively. The initial state is uncorrelated with the white noises processes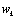 and
and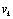 and
and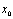 is a Gaussian random variable with
is a Gaussian random variable with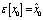 and
and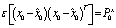 where
where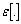 denotes the expectation operator. We denote by
denotes the expectation operator. We denote by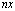 ,
,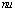 ,
,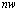 ,
, 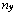 and
and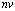 respectively, the dimensions of the state, the input vectors, process noise vectors, the measurement and measurement noise vectors. Let
respectively, the dimensions of the state, the input vectors, process noise vectors, the measurement and measurement noise vectors. Let 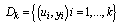 denote the available measurement information at the time k :The type of faults of interest here are the failure type where the system parameter values to in new value reflected in a change in the state transition function
denote the available measurement information at the time k :The type of faults of interest here are the failure type where the system parameter values to in new value reflected in a change in the state transition function 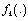 at time k and the measurement function
at time k and the measurement function 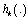 at time k such fault can be detected using the state observer approach.
at time k such fault can be detected using the state observer approach.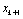 , based on the input output data D observed up to instant k+, more precisely, to estimate the conditional probability density function
, based on the input output data D observed up to instant k+, more precisely, to estimate the conditional probability density function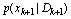 . In general, no accurate tow estimator exists, the Minimum Mean Squared Error estimate (MMSE) and the Maximum a Posteriori Probabilities (MAP) estimate for nonlinear stochastic systems, even if the noises are assumed to be Gaussian or non-Gaussian as follows
. In general, no accurate tow estimator exists, the Minimum Mean Squared Error estimate (MMSE) and the Maximum a Posteriori Probabilities (MAP) estimate for nonlinear stochastic systems, even if the noises are assumed to be Gaussian or non-Gaussian as follows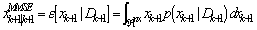
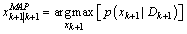
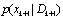 of
of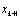 based on the observation sequence
based on the observation sequence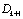 , can be basically achieved by performing three recursive steps. It can be expressed as followsStep (1). Initialization:
, can be basically achieved by performing three recursive steps. It can be expressed as followsStep (1). Initialization: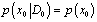
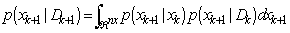
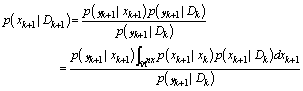
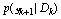 the normalizing constant
the normalizing constant 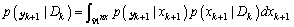
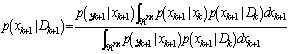
 k + 1, go to Step (2).In steps (2) and (3)
k + 1, go to Step (2).In steps (2) and (3) 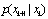 is defined by the state function, Eq. 1 and
is defined by the state function, Eq. 1 and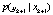 is the conditional density of observation, given the state at time k+1, Eq. 2. Similarly the posterior probability density for smoothing
is the conditional density of observation, given the state at time k+1, Eq. 2. Similarly the posterior probability density for smoothing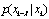
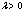 and filtering,
and filtering,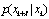 ,
, 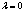 can be defined.However this paper is only concerned with prediction, and thus the only situation of interest is where
can be defined.However this paper is only concerned with prediction, and thus the only situation of interest is where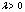 . The posteriori probability density given by the above steps is exact, but in general, it can be viewed as an infinite dimensional system, thus not implementable. There is however a severe problem in Baysian state estimation for nonlinear systems that makes is difficult to readily the equations (6) and (7) because they involve high dimensional integrations. The most important special case is when the system is linear, i.e,
. The posteriori probability density given by the above steps is exact, but in general, it can be viewed as an infinite dimensional system, thus not implementable. There is however a severe problem in Baysian state estimation for nonlinear systems that makes is difficult to readily the equations (6) and (7) because they involve high dimensional integrations. The most important special case is when the system is linear, i.e, 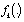 and
and 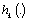 are linear and one assumes that the noise and the initial state are Gaussian,i.e.,
are linear and one assumes that the noise and the initial state are Gaussian,i.e.,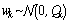
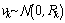 . The solution is provided by the Kalman filter. More details and background for this filter can be found in[13]. We also describe how, when the analytic solution is intractable, Extended Kalman filter, and Particle filter approximate the optimal Bayesian solution.
. The solution is provided by the Kalman filter. More details and background for this filter can be found in[13]. We also describe how, when the analytic solution is intractable, Extended Kalman filter, and Particle filter approximate the optimal Bayesian solution.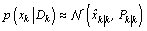
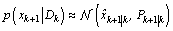
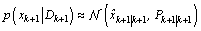
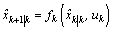
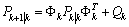
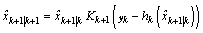
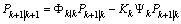
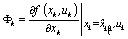
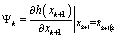 The residual or the innovation is then,
The residual or the innovation is then,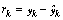
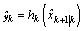
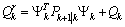
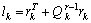
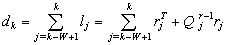
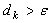
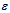 being the threshold. When using extended kalman filter to estimate the states and hence
being the threshold. When using extended kalman filter to estimate the states and hence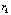
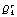 . The measure Lk will thus consist of fluctuations which can in turn lead to higher false alarm rates and also to faults not being detected.
. The measure Lk will thus consist of fluctuations which can in turn lead to higher false alarm rates and also to faults not being detected.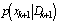 of the state, given the measured output
of the state, given the measured output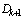 and assuming conditional independence of the measurement sequence, given the states. The PF works in two stages: 1) The prediction stage uses the state-transition model in(1) to predict the state pdf one step ahead. The pdf obtained is called the prior.2) The update stage uses the latest measurement to correct the prior via the Bayes rule. Particle filters represent the pdf by N random samples (particles)
and assuming conditional independence of the measurement sequence, given the states. The PF works in two stages: 1) The prediction stage uses the state-transition model in(1) to predict the state pdf one step ahead. The pdf obtained is called the prior.2) The update stage uses the latest measurement to correct the prior via the Bayes rule. Particle filters represent the pdf by N random samples (particles) 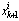 with their associated weights
with their associated weights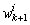 , normalized so that
, normalized so that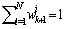 . At time instant k, the prior pdf
. At time instant k, the prior pdf 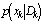 is represented by N samples
is represented by N samples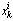 and the corresponding weights
and the corresponding weights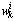 . To approximate the posterior
. To approximate the posterior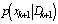 , new samples
, new samples 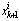 and weights
and weights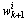 are generated.Samples
are generated.Samples 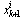 are drawn from a (chosen) importance density function
are drawn from a (chosen) importance density function 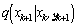 , and the weights are updated, using the current measurement
, and the weights are updated, using the current measurement 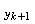
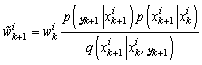
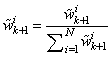 The posterior pdf is represented by the set of weight samples, conventionally denoted by:
The posterior pdf is represented by the set of weight samples, conventionally denoted by: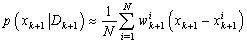
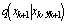 equal to the state-transition pdf
equal to the state-transition pdf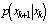 . The weight update equation (23) then becomes:
. The weight update equation (23) then becomes: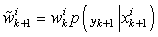
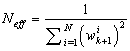 Thus, the degeneracy phenomenon can be detected when Neff < Nthr where Nthr is the threshold value Nthr
Thus, the degeneracy phenomenon can be detected when Neff < Nthr where Nthr is the threshold value Nthr 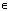 [1, N]. When such condition is encountered, the resampling algorithm is just applied. For more details on particle filters, refer to[3,10,15].
[1, N]. When such condition is encountered, the resampling algorithm is just applied. For more details on particle filters, refer to[3,10,15]. are generated as particle filter prediction step.• Step 2: Output predictionThe output prediction samples
are generated as particle filter prediction step.• Step 2: Output predictionThe output prediction samples 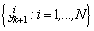 are generated using the measurement equation in (2), where,
are generated using the measurement equation in (2), where,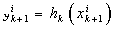 • Step 3: Residual generationSample mean of the predicted measurements is computed as,
• Step 3: Residual generationSample mean of the predicted measurements is computed as, 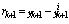 • Step 4: Fault detectionCompute the likelihood is given by,
• Step 4: Fault detectionCompute the likelihood is given by,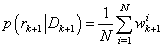 The windowed likelihood is
The windowed likelihood is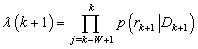 Or equivalently the negative log likelihood is
Or equivalently the negative log likelihood is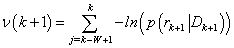 is computed and the condition
is computed and the condition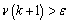 is tested for the presence of fault.
is tested for the presence of fault. Here
Here is the unknown fault parameter vector to be estimated. Because
is the unknown fault parameter vector to be estimated. Because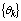 is not ergodic,
is not ergodic, 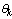 cannot be tracked in the PF algorithm. Therefore, in order to track the dynamics of
cannot be tracked in the PF algorithm. Therefore, in order to track the dynamics of 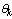 an artificial dynamic noise vector is added to the model of the unknown parameter
an artificial dynamic noise vector is added to the model of the unknown parameter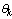 :
: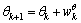
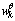 is the parameter noise. Then the augmented system and measurement functions are respectively defined as
is the parameter noise. Then the augmented system and measurement functions are respectively defined as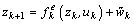
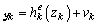
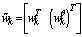 . Because
. Because 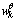 is artificial, its statistical properties need to be determined. In this paper, we assume that
is artificial, its statistical properties need to be determined. In this paper, we assume that 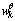 is a zero-mean Gaussian white noise process that is introduced for parameter evolution to allow the exploration of the parameter space. Given the above system representation (27) and (28), the particle filter outlined in this setion5, can be used to obtain the sample-based joint probability function density of the state x and parameter vector
is a zero-mean Gaussian white noise process that is introduced for parameter evolution to allow the exploration of the parameter space. Given the above system representation (27) and (28), the particle filter outlined in this setion5, can be used to obtain the sample-based joint probability function density of the state x and parameter vector such an estimate based on particle filter algorithm is given by,
such an estimate based on particle filter algorithm is given by,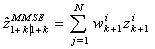
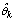 can be compared to the nominal values
can be compared to the nominal values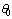 as a means for fault detection and its deviation
as a means for fault detection and its deviation 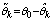 .
.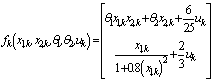
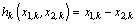
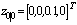 ,
, 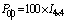 . The measurement and process noise signals are both set to be Gaussian with covariance matrices,
. The measurement and process noise signals are both set to be Gaussian with covariance matrices,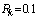
 ,The input and observation shown in Fig.1. The time index is incremented as k=0,…….,200. The nominal values of the parameters are
,The input and observation shown in Fig.1. The time index is incremented as k=0,…….,200. The nominal values of the parameters are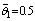 and
and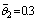 . In the simulation, the length of the data window for WSSR calculation is N1=30 and the number of particles in the particle filter is N = 600. The fault is simulated to occur at time k= 100 at which time the parameter
. In the simulation, the length of the data window for WSSR calculation is N1=30 and the number of particles in the particle filter is N = 600. The fault is simulated to occur at time k= 100 at which time the parameter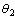 jumps from a value of
jumps from a value of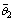 to
to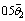 while
while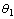 remains unchanged. The Weighted Sum Squared Residual (WSSR) results for the EKF is shown in Figure 2 and the negative log likelihood for the particle filter in Figure 3. The EKF based approach fails to detect the occurrence of the fault around k =100 as evidenced by Figure 2 where there is no significant change in WSSR. The detection performance is unacceptable. On the other hand, the particle filter detects the fault at k =104 a threshold value of
remains unchanged. The Weighted Sum Squared Residual (WSSR) results for the EKF is shown in Figure 2 and the negative log likelihood for the particle filter in Figure 3. The EKF based approach fails to detect the occurrence of the fault around k =100 as evidenced by Figure 2 where there is no significant change in WSSR. The detection performance is unacceptable. On the other hand, the particle filter detects the fault at k =104 a threshold value of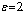 . The change in log likelihood is quite pronounced following the onset of the fault. The combined fault detection isolation (FDI) scheme proposed in section7was also applied to the above example.
. The change in log likelihood is quite pronounced following the onset of the fault. The combined fault detection isolation (FDI) scheme proposed in section7was also applied to the above example.

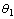
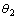 estimates from the EKF and true values, (b) weight sum squared residual (WSSR) -EKF
estimates from the EKF and true values, (b) weight sum squared residual (WSSR) -EKF
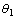
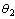 estimates from the ParticleFilter and true values, (b )Negative log likelihood - Particle Filter
estimates from the ParticleFilter and true values, (b )Negative log likelihood - Particle Filter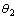 is tracked following an initial transient and the estimate for the other parameter
is tracked following an initial transient and the estimate for the other parameter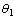 hovers around the nominal parameter. The PF successfully tracks the system parameter, while this is not seen for EKF (Figure3). Thus we can safely conclude that the fault in the system is due to the change in the parameter
hovers around the nominal parameter. The PF successfully tracks the system parameter, while this is not seen for EKF (Figure3). Thus we can safely conclude that the fault in the system is due to the change in the parameter 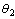
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML