-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2012; 2(2): 15-22
doi: 10.5923/j.ajsp.20120202.03
Efficient Cryptosystem Based on Chaotic Sequences Sorting
J. S. Armand Eyebe Fouda 1, J. Yves Effa 2, Bertrand Bodo 1, Maaruf Ali 3
1Department of Physics, University of Yaoundé I, Yaoundé, P.O. Box 812, Cameroon
2Department of Physics, University of Ngaoundéré, Ngaoundéré, P.O. Box 454, Cameroon
3College of Computer Science and Engineering, University of Ha’il, Ha’il, Kingdom of Saudi Arabia
Correspondence to: J. Yves Effa , Department of Physics, University of Ngaoundéré, Ngaoundéré, P.O. Box 454, Cameroon.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
It is commonly known that mathematical representation of chaotic systems can be used as good candidates for information security. In this paper, we propose an image encryption algorithm based on the use of chaotic sequences sorted by ascending or descending order. The permutation key is defined as a distribution of indices derived from the sorting. This method allows us to easily achieve high performance of pseudorandom permutation through any type of chaotic systems using the true precision of the computer; high-speed encryption algorithm which could meet one of the multimedia encryption specific requirements such as the real-time constraint and high robustness against statistical cryptanalysis. The efficiency of the proposed algorithm is studied in the cases of the piecewise linear chaotic map (PWLCM) and the hyperchaotic Lorenz system. Statistical analyses of the simulation results confirm a high security level of the proposed cipher.
Keywords: Chaos Cryptography, Cryptanalysis, Random Permutation, Adaptable Cipher
Article Outline
1. Introduction
- Image encryption requires modifying the entropy of the image, thus, its histogram, by creating new words or adjusting the probabilities of the existing words when the whole alphabet is already used. The image encryption methods which are based on chaotic systems attract attention due to their effectiveness for digital multimedia encryption whilst exhibiting the required enhanced sensitivity to initial conditions and system parameters (ergodicity and mixing)[1-4]. Most of the existing chaotic cryptosystems are based on the pixels permutation and the use of the XOR logical function for bit substitution[5-11]. In the Xiang[12] algorithm for example, blocks of bits are circularly shifted and the number of bits to be shifted is randomly determined by the chaotic value obtained from a logistic map after 70 iterations. Even though this procedure is efficient, the total number of permutations is reduced by the precision used for the digitization of the chaotic values- thus leading to a poor exploitation of the alphabet. In order to increase the number of permutations to achieve a stronger encryption, pixels are combined to form complex blocks of 32 or 64 bits (groups of 4 or 8 pixels). In the Socek algorithm[13], the permutational method is a computational approach of degree eight, where indices of bits are permutated using the chaotic values. Although this algorithm is efficient and fast, it is disadvantageous in the increased propagation of errors when a bit error occurs in the encrypted image during transmission. Recently, Abir et al.[14] proposed a method with no propagation error by combining the Xiang and Socek permutation algorithms. The corresponding encryption entropy was greater than the Xiang algorithm result.Bits permutation is the main part of encryption algorithms; therefore, it is important to develop efficient permutation techniques. The pixel combination provides satisfactory results in terms of permutation possibilities; unfortunately, this procedure is limited by the propagation errors. These errors increase as the number of combined pixels increases. Permutation techniques require that the bits be rearranged in their exact initial order during decryption which justifies the complexity of encryption algorithms. To avoid permutation errors, cryptographers make use of the cyclic bits and pixels permutation methods[14]. Though, these permutation techniques are chaos-controlled, the number of permutations remains less than
 - that is the total number of possibilities for each pixel. For the Xiang permutation algorithm for example, the cyclic shift concerns blocks of bits and the number of bits to be shifted is controlled by the logistic map. For instance, for a block of N-bits divided into two blocks of length N1 and N2, the total number of permutation is
- that is the total number of possibilities for each pixel. For the Xiang permutation algorithm for example, the cyclic shift concerns blocks of bits and the number of bits to be shifted is controlled by the logistic map. For instance, for a block of N-bits divided into two blocks of length N1 and N2, the total number of permutation is 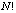 whereas using the cyclic shift the number of permutations is only
whereas using the cyclic shift the number of permutations is only 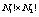 (
(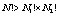 ). Whatever the size of block of bits considered, for images encoded on eight bits the significant number of bit permutation per pixel cannot exceed
). Whatever the size of block of bits considered, for images encoded on eight bits the significant number of bit permutation per pixel cannot exceed  .P. Fei et al. also proposed an algorithm for image encryption[15] in which the aim was to randomly encrypt the three colours red (R) green (G) and blue (B) with three chaotic systems. The computational time was relatively large and the algorithmic steps could not be repeated for more security, as it is the case for many other encryption algorithms. Moreover, the correlation of adjacent pixels presented by this method could be improved, according to those presented in[14].Chen et al.[16] proposed a symmetric cipher in which a two-dimensional chaotic map is generalized to three dimensions for designing a secure real-time image encryption scheme. This approach employs the three-dimensional cat map to shuffle the positions of the image pixels and another chaotic map to confuse the relationship between the original and the ciphered images. Guan et al.[17] presented an image encryption scheme in which shuffling the positions and changing the grey values of image pixels are combined to confuse the relationship between the plain-image and ciphered image.The aims of the proposed algorithm are to easily achieve high performance of pseudorandom permutation through utilization of any type of chaotic systems using the true precision of the computer (without the need for digitization); high-speed encryption algorithm which could meet one of the multimedia encryption specific requirements such as the demanding real-time constraint and high robustness against statistical cryptanalysis.The work is organized as follows: the algorithm is proposed in Section Two; the results are discussed in Section Three and the conclusions are made in Section Four.
.P. Fei et al. also proposed an algorithm for image encryption[15] in which the aim was to randomly encrypt the three colours red (R) green (G) and blue (B) with three chaotic systems. The computational time was relatively large and the algorithmic steps could not be repeated for more security, as it is the case for many other encryption algorithms. Moreover, the correlation of adjacent pixels presented by this method could be improved, according to those presented in[14].Chen et al.[16] proposed a symmetric cipher in which a two-dimensional chaotic map is generalized to three dimensions for designing a secure real-time image encryption scheme. This approach employs the three-dimensional cat map to shuffle the positions of the image pixels and another chaotic map to confuse the relationship between the original and the ciphered images. Guan et al.[17] presented an image encryption scheme in which shuffling the positions and changing the grey values of image pixels are combined to confuse the relationship between the plain-image and ciphered image.The aims of the proposed algorithm are to easily achieve high performance of pseudorandom permutation through utilization of any type of chaotic systems using the true precision of the computer (without the need for digitization); high-speed encryption algorithm which could meet one of the multimedia encryption specific requirements such as the demanding real-time constraint and high robustness against statistical cryptanalysis.The work is organized as follows: the algorithm is proposed in Section Two; the results are discussed in Section Three and the conclusions are made in Section Four.2. Proposed Encryption Algorithm
- The proposed algorithm in this paper is divided into two main steps: the reduction of the correlation between pixels and the increment of the entropy through a random distribution of the indices derived from an ascending or descending sorting of chaotic sequences. The complete algorithm is presented as follows:1. Define a window of size m-by-n which could match a part or the whole plaintext image, then reshape it so as to obtain a 1-D signal of length
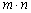 ; 2. Chose a 256-key and generate a chaotic sequence of length
; 2. Chose a 256-key and generate a chaotic sequence of length  , then sort it in the ascending or descending order and save the corresponding distribution of indices
, then sort it in the ascending or descending order and save the corresponding distribution of indices 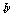 as a permutation key;3. Reshape the whole image into a 1-D signal of length L and split it into windows of length
as a permutation key;3. Reshape the whole image into a 1-D signal of length L and split it into windows of length 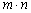 ; 4. Shuffle pixels in each of the signal window with the permutation key;5. Mask the pixels in each of the shuffled window with the values in
; 4. Shuffle pixels in each of the signal window with the permutation key;5. Mask the pixels in each of the shuffled window with the values in 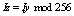 ;6. Generate two chaotic integers k and l less than L and permute blocks of pixels
;6. Generate two chaotic integers k and l less than L and permute blocks of pixels  and
and 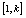 , thereafter
, thereafter  and
and 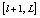 in the whole image;7. Repeat steps four to six p times;8. Reshape the shuffled 1-D signal into 2-D image (ciphered image).Initial conditions and control parameters of the chaotic systems constitute the secret key of the proposed cipher.Steps one to three of the algorithm concern the initialization and steps four to six perform the pixels and bits shuffling. The digitization of the chaotic sequence values does not allow the exploitation of the real accuracy of the computer like sorting. Therefore, digitization appears only in step six, which increases the sensitivity of our algorithm to any fluctuation that could occur in the chaotic sequence. Presented in this form, the proposed algorithm can be efficiently combined with any type of chaotic system.
in the whole image;7. Repeat steps four to six p times;8. Reshape the shuffled 1-D signal into 2-D image (ciphered image).Initial conditions and control parameters of the chaotic systems constitute the secret key of the proposed cipher.Steps one to three of the algorithm concern the initialization and steps four to six perform the pixels and bits shuffling. The digitization of the chaotic sequence values does not allow the exploitation of the real accuracy of the computer like sorting. Therefore, digitization appears only in step six, which increases the sensitivity of our algorithm to any fluctuation that could occur in the chaotic sequence. Presented in this form, the proposed algorithm can be efficiently combined with any type of chaotic system.2.1. Permutation of Pixels in a Window
- The technique used for the permutation of pixels is based on the ascending or descending sorting of a chaotic sequence. By the chaotic scheme of the values in a generated sequence, we obtained a pseudorandom distribution of the positions (indices) of these values. We defined
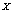 as a chaotic sequence and
as a chaotic sequence and 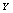 as the corresponding sorted sequence. We also defined
as the corresponding sorted sequence. We also defined 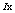 as the distribution of values in the sequence
as the distribution of values in the sequence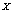 ,was so
,was so rted by ascending. Sequences
rted by ascending. Sequences 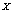 and
and 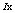 can then be expressed by:
can then be expressed by: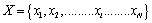 | (1) |
 | (2) |
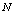 being the length of
being the length of 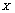 . In the sequence
. In the sequence 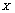 , values were randomly distributed and these values were all different according to the statistic properties of the chaotic system and the precision of the computer. Sorting the sequence
, values were randomly distributed and these values were all different according to the statistic properties of the chaotic system and the precision of the computer. Sorting the sequence 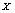 by ascending, we obtained a new sequence
by ascending, we obtained a new sequence 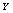 in which the indices (positions) of the values were randomly distributed:
in which the indices (positions) of the values were randomly distributed: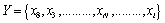 | (3) |
 be the sequence containing the position of the values of
be the sequence containing the position of the values of 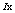 in the sequence
in the sequence 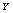 , from (3),
, from (3), 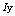 was expressed as:
was expressed as: | (4) |
 differs from a sequence to another when
differs from a sequence to another when 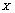 is a chaotic sequence. In this point of view,
is a chaotic sequence. In this point of view, 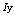 can be seen as a random variable and the number of probable events is equal to the number of permutations of the indices, this means
can be seen as a random variable and the number of probable events is equal to the number of permutations of the indices, this means 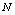 .To a sequence
.To a sequence  obtained by reshaping an image
obtained by reshaping an image 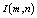 , where
, where  , we applied the distribution
, we applied the distribution 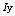 . Values in
. Values in 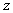 were initially ranked by ascension of the corresponding indices:
were initially ranked by ascension of the corresponding indices: | (5) |
 with
with 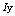 , we obtained a new sequence
, we obtained a new sequence 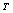 such that:
such that: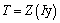 | (6) |
 corresponds to the permuted image and the reconstruction of
corresponds to the permuted image and the reconstruction of 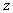 cannot be made unless the distribution
cannot be made unless the distribution  is determined. Pixels permutation does not modify the entropy of the image, but it reduces the correlation between adjacent pixels. Increasing the image entropy requires the construction of new words in the image. This result can be performed by bit operations - hence the step of masking.
is determined. Pixels permutation does not modify the entropy of the image, but it reduces the correlation between adjacent pixels. Increasing the image entropy requires the construction of new words in the image. This result can be performed by bit operations - hence the step of masking.2.2. Masking the Pixel in a Window
- Contrary to the indices permutation technique, the XOR can only be combined with binary values. For this purpose, we used the distribution of indices
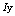 for the pixels masking. Since this distribution presents values ranging from 1 to
for the pixels masking. Since this distribution presents values ranging from 1 to  , it is necessary to bring back values greater than 255 among[0, 255], according to the image format. The setof values used for this operation is given by:
, it is necessary to bring back values greater than 255 among[0, 255], according to the image format. The setof values used for this operation is given by: | (7) |
2.3. Permuting Blocks of Pixels
- Steps four and five subdivided the whole image into blocks of small sizes. In order to increase the randomness in the entire ciphered image, pixels should pass from a block to another. For this purpose, two chaotic values were generated and digitized such that the corresponding digital values (natural numbers) k and l correspond to indices of pixels in the whole 1-D image (of length L). These values are used to permute blocks of pixels
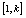 and
and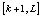 first and for the second time blocks
first and for the second time blocks 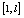 and
and 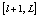 in the whole image. The initial condition of the chaotic system used for the generation of k and l are derived from the following relation:
in the whole image. The initial condition of the chaotic system used for the generation of k and l are derived from the following relation: | (8) |
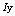 . Choosing large number of rounds makes it impossible for any statistical attack[18].
. Choosing large number of rounds makes it impossible for any statistical attack[18].2.4. Key Schedule
- By today’s standards, a key of 128 bits or 256 bits is required for symmetric-key cryptosystems[19]. We used an external 256-bit key (
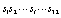 , where Si are ASCII symbols) to derive initial conditions and control parameters of the chaotic system. The key is divided into two blocks of 16 ASCII symbols for the determination of the system control parameter and the initial condition respectively. For each block of 128 bits (corresponding to 16 ASCII symbols), we defined:
, where Si are ASCII symbols) to derive initial conditions and control parameters of the chaotic system. The key is divided into two blocks of 16 ASCII symbols for the determination of the system control parameter and the initial condition respectively. For each block of 128 bits (corresponding to 16 ASCII symbols), we defined: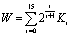 | (9) |
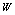 is the value from which the control parameters and initial conditions will be deduced, depending on the chaotic system. By considering the possible maximum value of ASCII symbols equal to 255 and the upper limit of the weight coefficient
is the value from which the control parameters and initial conditions will be deduced, depending on the chaotic system. By considering the possible maximum value of ASCII symbols equal to 255 and the upper limit of the weight coefficient 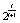 equal to 2, the value of the W presents an upper limit
equal to 2, the value of the W presents an upper limit 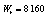 , which is used for the normalization of W.
, which is used for the normalization of W.3. Test Results and Security Analysis
- A good encryption scheme should resist any kind of known attacks: known-plaintext attack, ciphertext-only attack, statistical attack, differential attack and brute-force attack. In this section, some security analysis results on the scheme are described, including some important ones like key space analysis, statistical analysis, differential analysis, number of pixel change rate (NPCR) and unified average changing intensity (UACI) for one pixel difference in the plain-text image. Two chaotic systems are used for this purpose: the PWLCM as discrete chaotic system and the hyperchaotic Lorenz system as chaotic continuous-time system. Three plain-images were selected for the evaluation of the proposed algorithm: the image of Lena (size
 ); the image of mandrill (size
); the image of mandrill (size 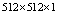 ) and a uniformly black image (size
) and a uniformly black image (size  ) whose statistical properties are summarized in Table 1.
) whose statistical properties are summarized in Table 1.
|
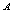 and
and 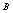 is defined by:
is defined by: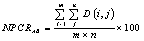 | (10) |
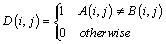 | (11) |
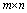 being the size of images and . Similarly, the unified average changing intensity (UACI) is defined by:
being the size of images and . Similarly, the unified average changing intensity (UACI) is defined by: | (12) |
 | (13) |
 is the probability of the event
is the probability of the event  and b the number of bits.
and b the number of bits.3.1. Case of the PWLCM
- The PWLCM is defined by the following equation:
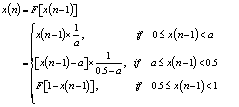 | (14) |
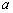 is within
is within 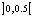 and its initial condition chosen within the interval
and its initial condition chosen within the interval 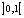 [20]. For this purpose, the control parameter and the initial condition
[20]. For this purpose, the control parameter and the initial condition 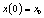 are deduced from the key through the following relation:
are deduced from the key through the following relation: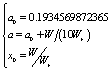 | (15) |
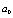 is a constant chosen such that the behavior of the PWLCM remains chaotic for any key derived from (9). In step six was also used the PWLCM with
is a constant chosen such that the behavior of the PWLCM remains chaotic for any key derived from (9). In step six was also used the PWLCM with  as initial condition.Two encryption sub-keys
as initial condition.Two encryption sub-keys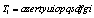 and
and 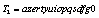 were used respectively for the control parameter and the initial condition, thus forming a 32 ASCII symbols key T1T2:(
were used respectively for the control parameter and the initial condition, thus forming a 32 ASCII symbols key T1T2:( ).
).3.1.1. Key Space Analysis
- a) The Key SpaceThe proposed scheme has a 256-bit key corresponding to 32 ASCII symbols. The key space is the number of sets of 32 ASCII symbols that can be built. In hexadecimal representation, the number of different combinations of secret keys is equal to
 , provided that the length of each block to be shuffled is such that
, provided that the length of each block to be shuffled is such that 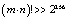 . By considering only symbols “a-z”, “A-Z” and “0-9”, the scheme presents
. By considering only symbols “a-z”, “A-Z” and “0-9”, the scheme presents  secret keys. A cipher with such a large key space can resist all present kinds of brute-force attack.b) Sensitivity of the KeyHigh key sensitivity is generally required for preventing adaptive chosen-plaintext attacks and linear cryptanalysis. The key T2 was partially changed to perform the test on the sensitivity of the key with the proposed approach. The sensitivity of the key is then performed according to the following steps:First the image of Lena is encrypted by using
secret keys. A cipher with such a large key space can resist all present kinds of brute-force attack.b) Sensitivity of the KeyHigh key sensitivity is generally required for preventing adaptive chosen-plaintext attacks and linear cryptanalysis. The key T2 was partially changed to perform the test on the sensitivity of the key with the proposed approach. The sensitivity of the key is then performed according to the following steps:First the image of Lena is encrypted by using 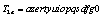 as key for initial condition;Then the least significant bit of T2 is changed, so that the initial key becomes
as key for initial condition;Then the least significant bit of T2 is changed, so that the initial key becomes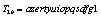 in this example, which is used to encrypt the same image of Lena;Finally, the above two ciphered images, encrypted by the two slightly different keys are compared.The number of rounds in this experiment is p=10. The results thus obtained are illustrated in Figure 1. From left to right and from top to bottom are presented the original image, the first and second encrypted images and the difference of the two encrypted images. The comparison of the ciphered images shows that the image encrypted by
in this example, which is used to encrypt the same image of Lena;Finally, the above two ciphered images, encrypted by the two slightly different keys are compared.The number of rounds in this experiment is p=10. The results thus obtained are illustrated in Figure 1. From left to right and from top to bottom are presented the original image, the first and second encrypted images and the difference of the two encrypted images. The comparison of the ciphered images shows that the image encrypted by 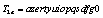 has 99.63% difference from the image encrypted by the key
has 99.63% difference from the image encrypted by the key 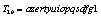 in terms of pixel grey scale values, although there is only one bit difference in the two secret keys.In order to quantify the dependency between the two ciphered images, the Pearson’s correlation coefficient
in terms of pixel grey scale values, although there is only one bit difference in the two secret keys.In order to quantify the dependency between the two ciphered images, the Pearson’s correlation coefficient 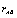 is used:
is used: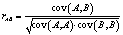 | (16) |
 | Figure 1. Key sensitive test (result 1). a) Plain-image, b) Image encrypted by T2a, c) Image encrypted by T2b, d) Difference of the two ciphered images |
 | Figure 2. Key sensitive test (result 2). a) Plain-image, b) Image encrypted by T2a, c) Image decrypted by T2a, d) Image decrypted by T2b |
 and the one used for decryption is
and the one used for decryption is  . From left to right and from top to bottom are presented the original, the encrypted, the decrypted and the unsuccessfully decrypted images. There is also only one bit difference between the two keys. The results in Table 2 and Figure 2 show that there is no relation existing amongst the encrypted images corresponding to a small change in the key, thus confirming that the proposed algorithm is highly key sensitive.
. From left to right and from top to bottom are presented the original, the encrypted, the decrypted and the unsuccessfully decrypted images. There is also only one bit difference between the two keys. The results in Table 2 and Figure 2 show that there is no relation existing amongst the encrypted images corresponding to a small change in the key, thus confirming that the proposed algorithm is highly key sensitive.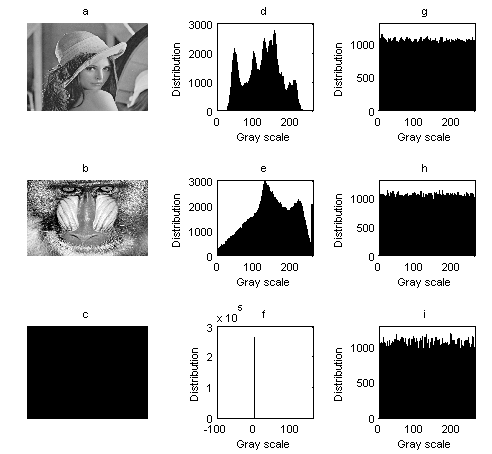 | Figure 3. Histograms of plain-images and ciphered images. a)-c) plain-images, d)-f) histograms of plain-images, g)-i) histograms of ciphered images |
3.1.2. Statistical Analysis
- a) Histogram of the Ciphered ImagesThe goal in encryption is to obtain some uniform histograms. Histograms of Several 256 gray-scale images of size 512×512 which have different contents were calculated. Typical examples among them are shown in Figure 3. From this figure, the histograms of the ciphered images are fairly uniform and significantly different from those of the plain-images. Although distributive characters of plain-images histograms are all different, the histograms of ciphered images are all fairly uniform, thus making difficult deducing the secret key from the cipher-text during the known/chosen plaintext attacks.b) Correlation of Two Adjacent PixelsThe correlation distributions of two horizontally adjacent pixels of plaintext and ciphered images are depicted in Figure 4, where the dispersion of the pixels after encryption can be appreciated. The correlation coefficients corresponding to the image of Lena for example are 0.9721 and 0.0010, respectively. Similar results for vertical and diagonal directions were obtained and are presented in Table 3. The analysis of correlation coefficients proves that the proposed encryption technique satisfies zero co-correlation property, thus its robustness against statistical attacks.
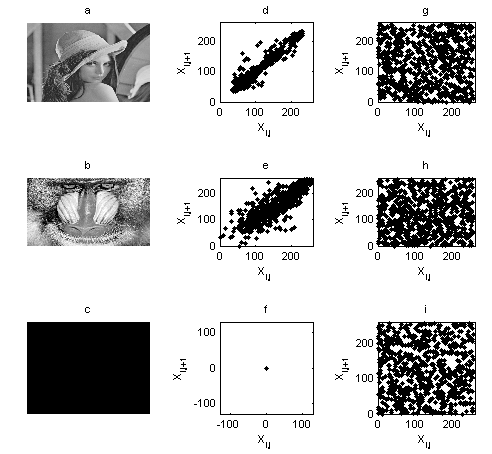 | Figure 4. Distribution of horizontally adjacent pixels in plaintext and ciphered images. a)-c) plain-images, d)-f) correlations in plain-images, g)-i) correlation in ciphered images |
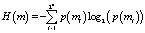 | (17) |
|
|
| ||||||||||||||||||||||||||||
3.1.3. Differential Attack
- One of the desirable properties of the cipher is its sensitivity to small changes in the plain-image (single pixel change). In order to test the influence of one-pixel change in the plain-image, encrypted by the proposed scheme, NPCR and UACI of two ciphered images whose corresponding plain-images have only one pixel difference are compared (see Table 6). NPCR for all the images are over 99.5%, showing that the encryption scheme is very sensitive with respect to small pixel changes in the plain-image. UACI values are all close to the ideal value of 33.33%, indicating that the rate of one pixel change is very large. These values of NPCR and UACI, in the case of one pixel change, confirm the high sensitivity of the proposed algorithm with respect to the plain-image, hence its robustness against differential attacks.
|
3.1.4. Effect of the Size of the Window and the Number of Rounds
- For a high security level, it is necessary to recursively repeat steps 4 to 6 p times. p is considered to be a security parameter. The size of the window can be considered as another security parameter as it allows considerable increase of the number of permutations of the pixels as well as the randomness of the values used for bit substitution. The results presented above were obtained with
 rounds and a window of size
rounds and a window of size  pixels. Now, let us study the effect of these two parameters on the ciphered image of the mandrill. Figure 5 shows the behaviors of correlation coefficients of adjacent pixels and correlation between plaintext and ciphered images in terms of the number of rounds and the size of the window. From left to right, the columns represent respectively the correlation of horizontally, vertically and diagonally adjacent pixels; the fourth column represents the correlation between plaintext and ciphered images. From top to bottom, are presented in each row, the results of windows of size 32×32, 64×64, 128×128 and 256×256 pixels. It appears on this figure that the increase of the size of the permutation window allows the reduction of the correlation between adjacent pixels. The behavior of these correlation coefficients in terms of the number of rounds is not uniform; large number of rounds does not necessarily guarantee small correlation coefficients. However, the number of rounds should be greater than two for obtaining a high security level. The security level can also be strengthened in step six, by combining more than two permutations.
pixels. Now, let us study the effect of these two parameters on the ciphered image of the mandrill. Figure 5 shows the behaviors of correlation coefficients of adjacent pixels and correlation between plaintext and ciphered images in terms of the number of rounds and the size of the window. From left to right, the columns represent respectively the correlation of horizontally, vertically and diagonally adjacent pixels; the fourth column represents the correlation between plaintext and ciphered images. From top to bottom, are presented in each row, the results of windows of size 32×32, 64×64, 128×128 and 256×256 pixels. It appears on this figure that the increase of the size of the permutation window allows the reduction of the correlation between adjacent pixels. The behavior of these correlation coefficients in terms of the number of rounds is not uniform; large number of rounds does not necessarily guarantee small correlation coefficients. However, the number of rounds should be greater than two for obtaining a high security level. The security level can also be strengthened in step six, by combining more than two permutations.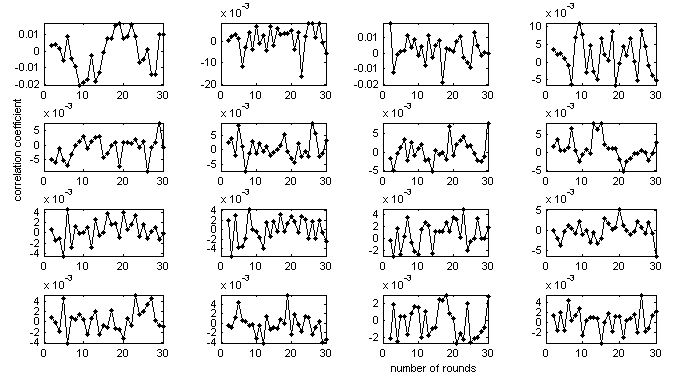 | Figure 5. Correlation coefficients in terms of the number of rounds and the size of the permutation window. column 1: correlation of horizontally adjacent pixels, column 2: correlation of vertically adjacent pixels, column 3: correlation of diagonally adjacent pixels, column 4: correlation between plaintext and ciphered image |
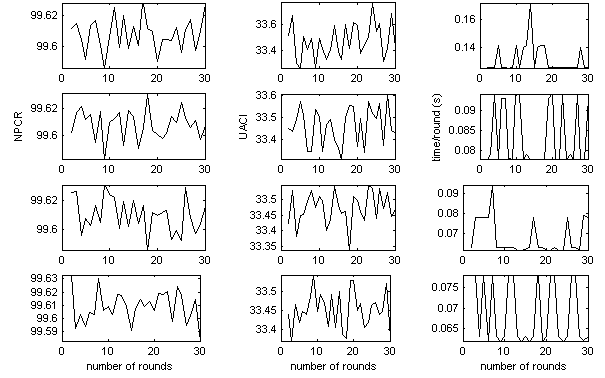 | Figure 6. NPCR (column 1), UACI (column 2) and average time/round (column3) in terms of the number of rounds and the size of the permutation window |
3.1.5. Speed Performance
- Apart from the security consideration, the running speed or execution of the algorithm is also an important aspect for a good encryption scheme. The simulator for the proposed scheme is implemented using Matlab 7.0. Although the algorithm was not optimized, performances measured on a 2.0 GHz Pentium Dual-Core with 3GB RAM running Windows XP are satisfactory. The average running speed, according to Figure 6, is 3.83MB/s per round in the case of using windows of size 256×256 pixels.
3.2. Case of the Hyperchaotic Lorenz System
- To show the adaptability of the algorithm to any type of chaotic system, a hyperchaotic Lorenz system (18) is used:
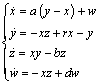 | (18) |
 ,
, 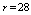 ,
, 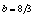 and
and  . The initial conditions are chosen such that
. The initial conditions are chosen such that  ,
,  ,
, 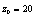 and
and 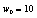 , the system exhibits hyperchaotic behavior as shown in[21]. As in the case of the PWLCM,
, the system exhibits hyperchaotic behavior as shown in[21]. As in the case of the PWLCM, 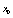 and
and  are varied as follows:
are varied as follows: | (19) |
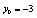 ,
,  ,
, 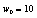 and:
and: 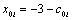 | (20) |
 | Figure 7. Encrypted and decrypted images by the hyperchaotic Lorenz system: a)-c) plain-images; d)-f) ciphered images; g)-i) deciphered images |
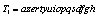 and
and 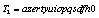 , and the results produced are given in Table 7. Figure 7 shows the corresponding encrypted and decrypted images presented as follows: plain-images are shown in the first column, the ciphered images in the second and the decrypted images in the third. For this experiment, the number of rounds was also equal to ten and only sequences given by the state
, and the results produced are given in Table 7. Figure 7 shows the corresponding encrypted and decrypted images presented as follows: plain-images are shown in the first column, the ciphered images in the second and the decrypted images in the third. For this experiment, the number of rounds was also equal to ten and only sequences given by the state 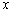 of the hyperchaotic sytem was used. The complexity of the algorithm could be enhanced by combining the four states
of the hyperchaotic sytem was used. The complexity of the algorithm could be enhanced by combining the four states 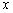 ,
, 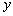 ,
, 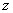 and
and 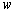 in steps four to six. According to Table 7, the sensitivity of the key remains higher, as in the case of the PWLCM.
in steps four to six. According to Table 7, the sensitivity of the key remains higher, as in the case of the PWLCM.
|
4. Conclusions
- This paper presented a permutation technique based on chaotic sequence sorting. It takes advantage of the true accuracy of the computer used for chaotic sequence generation, thus increasing the sensitivity of the key. It also presents the advantage that it can be combined with any type of chaotic system, which makes the proposed cipher easily adaptable. According to the execution time, the proposed scheme could guarantee real-time encryption. By comparison with other secured ciphers, the results obtained confirm the high robustness of the proposed scheme against known attacks. In the future, we plan to make the initialization phase dynamic, so as to increase the complexity of the proposed algorithm.
ACKNOWLEDGEMENTS
- We thank Dr. Mala William for his assistance in editing of this manuscript.
References
| [1] | L. Tang, “Methods for encrypting and decrypting MPEG video data efficiently”, in Proceedings of the 4th ACM International Multimedia Conference, pp. 219-230, 1996 |
| [2] | H. Cheng, and X. Li, “Partial encryption of compressed images and videos”, IEEE Transactions on Signal Processing, 48, pp. 2439-2451, 2000 |
| [3] | J.-C. Yen, and J.-I. Guo, “A new chaotic key-based design for image encryption and decryption”, in Proceedings of 2000 IEEE International Conference on Circuits and Systems, ISACS 2000, 4, pp. 49-52, 2000 |
| [4] | B. Bhargava, C. Shi, and S.-Y Wang, 2004, MPEG video encryption algorithms: Multimedia Tools and Applications, Kluwer Academic Publishers, 24(1), 57–79. |
| [5] | A. Riaz, and M. Ali, “Chaotic Communications, Their Applications and Advantages over Traditional Methods of Communication”, IEEE Commun. Syst., Networks Digital Signal Process, pp. 21-24, 2008 |
| [6] | G.J. Millérioux, M. Amigo, and J. Daafouz, 2008, A Connection between Chaotic and Conventional Cryptography, IEEE Trans. Circuits Syst., 55(6), 1695-1703. |
| [7] | L. Kocarev, 2001, Chaos Based Cryptography: A Brief Overview, IEEE Trans. Circuits Syst. Mag., 1(3), 6-21. |
| [8] | G. Alvarez, and S. Li, 2006, Some Basic Cryptographic Requirements for Chaos Based Cryptosystems, Int. J. Bifurcation Chaos, 16(8), 2129-2151. |
| [9] | T. Yang, C.W. Wu, and L.O. Chua, 1997, Cryptography Based on Chaotic Systems, IEEE Trans. Circuits Syst., 44(5), 469-472. |
| [10] | G. Jakimoski, and L. Kocarev, 2001, Chaos and Cryptography: Block Encryption Ciphers Based on Chaotic Maps. IEEE Trans. Circuits Syst., 48(2), 163-169. |
| [11] | S. Li, G. Chen, and X. Zheng, Chaos-based encryption for digital images and videos, in B. Furht and D. Kirovski (Eds.), Multimedia Security Handbook, 4 of Internet and Communications Series, Ch. 3, CRC Press, December 2004. |
| [12] | T. Xiang, X. Liao, K. Wong, G. Tang, and Y. Chen, “A Novel Block Cryptosystem Based on Iterating a Chaotic Map”, Phys. Lett. A 349, pp. 109-115, 2006 |
| [13] | D. Socek, S. Li, S. S. Magliveras, and B. Furht, “Enhanced 1-D Chaotic Key Based Algorithm for Image Encryption”, IEEE Security Privacy for Emerging Areas in Commun Networks, pp. 406-407, 2005 |
| [14] | A. Awad, and D. Awad, “Efficient image chaotic encryption algorithm with no propagation error”, ETRI journal 32, pp. 774-783, 2010 |
| [15] | P. Fei, S-S. Qiu, and L. Min, “An image encryption algorithm based on mixed chaotic dynamic systems and external keys”, IEEE int conf commun Circuits & systems, pp. 1135-1139, 2005 |
| [16] | G. Chen, Y. Mao, C.K. Chui, “A symmetric image encryption based on 3D chaotic maps”, Chaos, Solitons and Fractals, 21, pp. 749-761, 2004 |
| [17] | Z.H. Guan, F. Huang, and W. Guan, “Chaos-Based Image Encryption Algorithm”, Phys. Lett. A 346, pp. 153-157, 2005 |
| [18] | S.G. Lian, J. Sun, Z. Wang, “A block cipher based on a suitable use of chaotic standard map”, Chaos, Solitons and Fractals ,26, pp. 117-29, 2005 |
| [19] | D.R. Stinson, Cryptography: theory and practice, CRC Press, second edition, 2002 |
| [20] | H. Zhou, A design methodology of chaotic stream ciphers and the realization problems in finite precision, Ph.D. thesis, Department of Electrical Engineering, Fudan University, Shanghai, China, 1996. |
| [21] | D. Lu, A. Wang, and X. Tian, “Control and synchronization of a new hyperchaotic system with unknown parameters”, International Journal of Nonlinear Science 6, pp. 224-229, 2008 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML