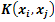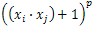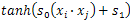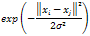1. Introduction

In various applications of document analysis, alphanumeric character recognition constitutes a very important step. For instance, in bank check processing this task is required for date recognition while in automatic mail sorting it is used to recognize addresses. However, the fact that characters are written in various manners by different scripts and different tools conducts to high similarity between some uppercase letters and digits such as Z and 2 or O and 0. Due to this ambiguity, classification systems fail commonly in discriminating uppercase letters from digits. Besides, in handwriting recognition robust classifiers should be used to achieve a satisfactory performance since conventional ones provide systematically insufficient recognition rates[1]. In the past recent years, attentions were focused on learning machines such as neural networks and hidden Markov models[2]. Currently, Support Vector Machines or SVMs are the best candidate for solving all handwriting recognition tasks with medium number of classes[3]. Specifically, SVMs were used for handwritten digit recognition in many research works[4,5]. In this work, we investigate their use for solving an alphanumeric character recognition which aims to discriminate uppercase Latin letters from digits. However, it is obviously known that such application handles commonly large scale databases whereas the SVM training time is quadratic to the number of data. For this reason, we investigate also, the applicability of N-SVM combination for alphanumeric classification. N-SVM is a neural-SVMs combination which was introduced for handwritten digit recognition in order to reduce the runtime and improve accuracy[6].

Furthermore, due to the large variability of alphanumeric characters the use of feature extraction schemes is a prerequisite to reach sufficient recognition accuracies. Specifically, feature extraction can alleviate some limitations related to script variations as well as to some segmentation errors. Many handwriting recognition research works have shown that earlier descriptors which were extensively used for pattern recognition such as geometric moments and generic Fourier descriptors cannot deal with characters ambiguity[7,8]. Thereby, more efficient descriptors were developed to allow invariance with respect to some variations of data. Recently, some features based on curvature or contour information were introduced for characters recognition. Among them, we note the ridgelet transform which showed high discrimination ability for printed Chinese characters[9]; curvature features for handwritten digit recognition[10] and wavelet packets for handwritten Arabic word recognition[11]. In fact, a good descriptor should be invariant with respect to some affine transformations such as small deformations, translations and rotations while being variable from a class to other. In this framework, tangent vectors which are based on invariance learning constitute one of the best descriptors for handwritten digit recognition[12,13]. Tangent vectors are computed by performing a set of affine transformations to each pattern. Then, classifiers are trained on the generated tangent samples to produce invariant decision functions. Since the results for handwritten digits were very promising, presently, we try to incorporate tangent vectors into the proposed alphanumeric character recognition system. Specifically, tangent similarities based on class-specific tangent vectors are used for both describing variability and reducing the size of data[14].

The rest of this paper is arranged as follows. Section 2 gives a brief review of SVM classifiers. Section 3 describes the N-SVM architecture while section 4 presents the tangent vector based similarities. The last sections summarize the experimental results and give the main conclusions of the paper.

2. Support Vector Machines

Support Vector Machines (SVMs) were designed to construct binary classifiers from a set of labeled training samples defined by: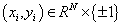, where 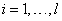(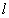is the number of training data). SVMs seek the linear separating hyperplane with the largest margin by solving the following optimization problem[3,15]:

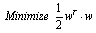(1)

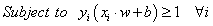(2)

T denotes the transpose, b is a bias while w is the normal to the hyperplane.

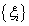When inequalities in (3) do not hold for some data, the SVM is non-linearly separable. Then, the margin of separation is said to be soft and non-separable data are handled by introducing a set of nonnegative slack variables into the decision surface[3]. Then, the goal is to find a hyperplane which minimizes misclassifications while maximizing the margin of separation such that:

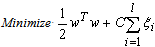(3)

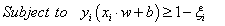(4)

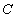is a user-defined parameter that controls the tradeoff between the machine complexity and the number of non-separable data[4]. Commonly, a dual Lagrangian formulation of the problem in which data appear in the form of dot products, is used:

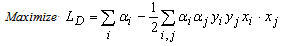(5)

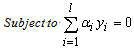(6)

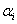where are Lagrange multipliers.

The dual problem is useful when data are not linearly separable in input space. In such a case, they are mapped into a feature space via a kernel function such that: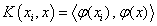. The dual problem becomes:

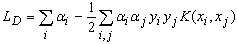(7)

Thereby, the decision function is expressed in terms of kernel expansion as:

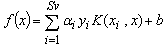(8)

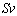is the number of support vectors which are training data for which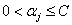. The optimal hyperplane corresponds to 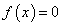while test data are classified according to:

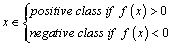(9)

All mathematical functions which satisfy Mercer’s conditions are eligible SVM-kernels. The similarity between data is expressed either in the form of a dot product or distance measure. The most commonly used kernels in pattern recognition are listed in Table (1).

Table 1. Some SVM kernels Noyau Polynomial: Pol Sigmoïde: Sig RBF Distance Négative: ND

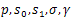: are user defined.

Furthermore, various approaches were proposed to extend SVMs for multi-class classification problems[16]. The One-Against-All (OAA) is the earliest and the most commonly used implementation. For a C-class problem, It performs M SVMs each of which is designed to separate a class from all the others. The c^th SVM is trained with all of the examples in the c^th class with positive labels, and all other examples with negative labels which leads to a computational time approximately about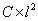. Then, data are assigned to the positive class with the highest output as:

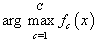(10)

Unfortunately, the time required for training the OAA-based SVM is a limitation for large scale databases. Recall that the training of a SVM is quadratic to the number of data[17]. This means that for OAA this time is multiplied by the number of classes. Thereby, for alphanumeric classification one must deal with this time complexity. Presently, we adopt a Neural-SVM (N-SVM) combination which aims to accelerate the runtime of SVMs. Since this combination was introduced for handwritten digit recognition we try to extend its use for alphanumeric character recognition. The N-SVM is briefly presented in the following section.

3. N-SVM Combination

The goal of N-SVM combination consists of reducing the runtime required by standard SVMs. This architecture was proposed for handwritten digit recognition where 5 dichotomies are randomly selected from the 45 possible dichotomies between numeral classes. Then, outputs of the SVMs trained over the selected dichotomies are handled by a neural network to produce an automatic decision about classes. The results obtained for USPS database highlighted the validity of this approach to reduce the runtime and improve the recognition accuracy[6]. Thus, for alphanumeric character recognition, which is a problem of 36 classes (10 digits and 26 uppercase letters), we develop 18 SVMs designed to independently separate pairs of classes. In summary, the N-SVM combination is composed of the following steps:

From the C×(C-1)/2 possible dichotomies (where C=36):

a) Select randomly a dichotomy and associate its classes 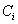and 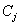to a SVM.

b) Delete classes 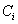and 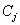from the set of classes.

c) Return to 1) if the number of selected pairs is less than C/2.

d) Train SVM classifiers over the selected pairs of classes.

e) Train a feed-forward neural network over SVM outputs.

The neural network is MultiLayer Perceptron (MLP) with a single hidden layer. The input layer contains 18 nodes, which receive SVM outputs whereas each node in the output layer corresponds to a numeral class from ‘0’ to ‘Z’. On the other hand, the number of hidden nodes is fixed experimentally. The MLP is trained by the standard back propagation algorithm including the momentum factor[18]. In addition, N-SVM system receives feature vectors which are constituted by tangent similarities with respect to all classes. The computation of such similarities is detailed in the following section.

4. Tangent Vector Based Similarities for SVMs

A priori knowledge was initially introduced to SVMs through the VSV approach which generates virtual samples from support vectors to enforce invariance around the decision boundary[19]. Indeed, invariance learning is based on the idea of learning small or local transformations, which leave the class of data unchangeable. To define these transformations, let 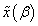denotes a transformation of a pattern 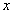that depends on a set of parameters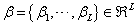. The linear approximation of 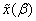using a Taylor expansion around 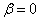can be written as[14]:

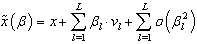(11)

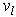are Tangent Vectors (TV) corresponding to partial derivatives of the transformation 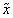with respect to 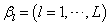so that :

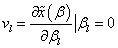(12)

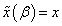Since terms of second order and higher in (11) are commonly neglected, for 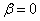while for small values the transformation does not change the class membership of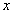. Hence, the linear approximation describes transformations such as translation, rotation and axis deformations by one prototype and its corresponding tangent vector. The first use of the TV was introduced through the so-called Tangent distance with the K-NN classifier[12]. This distance gave very good precisions for handwritten digit recognition but its time complexity was very important. Always for handwritten digit recognition, TV were used with SVM classifiers by introducing the Tangent distance into distance-based kernels such as RBF and negative distance[20]. However, the runtime of SVMs was significantly extended. More recently, a similarity and dissimilarity measures were introduced in order to allow using tangent vectors with all SVM kernels[21]. These measures are based on class-specific tangent vectors whose calculation is faster compared to the conventional scheme. Then, the time complexity is reduced but the runtime is still extended. In the present work, we aim to introduce the TV concept for alphanumeric character recognition without extending the runtime of SVMs and N-SVM. Specifically, we employ tangent similarities which are based on class-specific TV, as data features. The class-specific TV are computed as follows[14]. For a set of classes 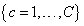with training data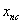 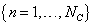, tangent vectors maximizing the dissimilarity between classes are chosen such that 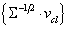are the eigenvectors with largest eigenvalues of the matrix :

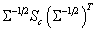(13)

: Covariance matrix computed from the full dataset.

: Class dependent scatter matrix given by: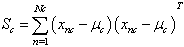

(14)

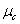: mean of the class.

It is straightforward to not that the number of TV should be obviously fixed by the user. In addition, each tangent vector refers to a transformation or specific variability knowledge whose number should be a priori chosen by the user. So, once estimated tangent vectors are incorporated into the covariance matrix specific to their classes such that[14]: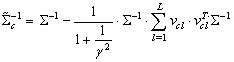

(15)

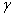: user defined parameter.

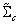: TV-based covariance matrix for the class.

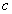Furthermore, the tangent similarity corresponds to the Tangent Vector-based Mahalanobis (TVM) distance of a pattern 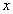with respect to a class 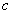becomes as:

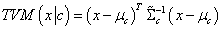(16)

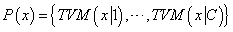In[14], these similarities were used to improve the likelihood function of Bayesian classifiers. For our part, we investigate their use as data features for training SVMs. The idea consists of substituting each pattern by a feature vector constituted by its TVM with respect to all classes. Then, to evaluate kernel functions the distance 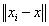is replaced by 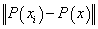while the dot product is substituted by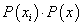. Note that benefits behind the use of such feature vectors are not only the implicit incorporation of invariance knowledge into SVMs but also the reduction of the data size. For alphanumeric character recognition the data size decreases from the character image size to a vector of 36 components (which is the number of classes). This makes the kernel evaluation as well as the training stage faster.

5. Experimental Results

Experiments are conducted on a dataset obtained by combining the well-known USPS handwritten digits with a set of cursive uppercase letters extracted from the C-Cube¹ (Cursive Character Challenge) database. The USPS is composed of 7291 training data and 2007 test data distributed on the 10 digits. These images are normalized to a size of 1616 pixels yielding 256 dimensional datum vector. For this reason, cursive uppercase letters of C-Cube database which come with varying sizes were normalized to the same size. This database contains 57293 cursive characters manually extracted from cursive handwritten words, including both upper and lower case versions of each letter. A set of 6018 uppercase letters were extracted and normalized to scale with the USPS data. The resulting database includes 11734 training samples and 3582 test samples. Figure 1 shows some examples which highlight the similarity between uppercase letters and digits.

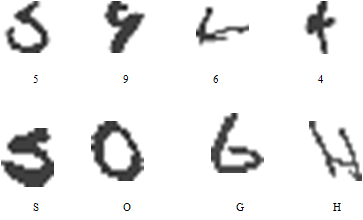Figure 1. Training samples from the USPS-C-Cube database.

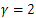We first performed a series of OAA and N-SVM runs to test out all possible configurations. Based on the corresponding error rates the best parameter values were selected as follows. The regularization parameter is fixed at 10 while kernel parameters are as: the sigma is 5 for RBF, d= 2 for polynomial kernel, for negative distance while sigmoid parameters are tuned to: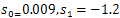. The neural network of N-SVM is a multilayer perceptron with 90 hidden nodes, the step size equals 0.08, the momentum is about 0.999 and the network is trained for 5000 iterations each of which corresponds to one processing of all training data through the network. In order to assess the behavior of tangent similarities with kernels based on a dot product and distance measure, we evaluated the Error Rate (ER) of both OAA and N-SVM by using kernels listed in Table (1). The results in terms of error rate are summarized in Table 1. In this test, the number of tangent vectors was arbitrarily fixed at 10.

Table 2. Error rates (%) provided by the training of tangent similarities using 10 tangent vectors RBF ND Pol Sig N-SVM 18,5 25,1 27,4 30,1 OAA 23,37 25,9 29,78 29,7

We can note that N-SVM outperforms the OAA with three kernels while it is slightly less accurate when using the sigmoid kernel. In addition, with both approaches, distance-based kernels deal better than dot product-based kernels where the RBF gives the best results. This kernel allows a gain which equals at least 7%.

In the second test, we investigated the behavior of OAA and N-SVM with respect to variations of tangent vectors number. This evaluation was carried out by using the RBF kernel with the precedent parametric selection. So, for both approaches, variations of error rate for different choices of the TV number are plotted in Figure 2. Roughly speaking, whatever the number of TV, OAA and N-SVM behave similarly but with different error rates. More precisely, the N-SVM combination gives a smaller error rate with a difference of 0.5%. We note also, the first TV improve the error rate which decreases with a factor of more than 4% with N-SVM and 6% with OAA. However, larger numbers of TV have a compounding effect since the error rate grows to more than 23% with both approaches. This outcome can be explained by the fact that TV are obtained by eigenvector decomposition. So, similarly to the principle component analysis the last eigenvectors are noisy and cannot bring any discriminating knowledge about data.

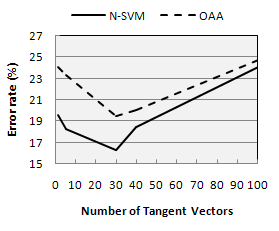Figure 2. Error rate variations according to the number of tangent vectors.

Finally, the best error rates are obtained for 30 TV. The results corresponding to this choice are reported in Table 3. In addition to error rates, this table reports the number of support vectors (#SV) per binary node (SVM), the Training Time (TT) expressed in hours as well as the recognition speed which is the Number of Recognized Characters (NRC) per second. As can be seen, N-SVM outperforms the OAA by 0.8% in error rate while being much faster. In fact, N-SVM training is 15 times faster because it employs 18 SVMs trained on different dichotomies while the neural network takes about 5 minutes. On the contrary, each SVM in the OAA is trained over the full dataset which yields a larger runtime. In consequent, N-SVM requires a smaller number of SV per SVM node the reason for which it has a higher recognition speed. Hence, roughly speaking N-SVM provides a significant acceleration of the runtime while being slightly more accurate.

Table 3. Performance evaluation of N-SVM and OAA using 30 TV OAA N-SVM Error rate (%) 19.12 16.30 #SV 137 68 TT (Hours) 169.3 6.52 NRC (second) 5.4 83.3

Furthermore, Figure 3 exhibits the error rates achieved in each class of interest by OAA and N-SVM. We remark that error rates respective to numeral classes are commonly smaller than those achieved for several uppercase letters which can reach 100%. This is the case of letters I, J and Z which are completely confused with other classes when using the OAA approach. This outcome is related to the number of training samples which is smaller (less than 20 training samples) compared to those of the other classes. In fact, in the considered dataset letter classes have smaller training sets compared to numeral classes. In addition, the normalization of letter images according to the size of USPS data altered the shape description of some letters which come with a very large initial size (images of 400×400 pixels). Nevertheless, N-SVM performs globally better than OAA since it gives lower error rates in 23 classes. Besides, it reduces significantly the error rates of classes which are completely confused by OAA (I,J, and Z).

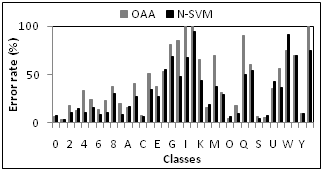Figure 3. Error rates respective to each class of interest.

6. Conclusions

In this paper, a fast and robust system for handwritten alphanumeric character recognition is proposed. Tangent similarities based on class specific tangent vectors are used to deal with data variability while N-SVM combination was used to accelerate the training stage of multi-class implementation of SVM (OAA). The N-SVM combination takes advantage from the high separation ability of SVM to separate the pairs of classes and the learning ability of neural network to construct an automatic decision about alphanumeric classes. The experimental analysis was conducted on a dataset obtained by combining two benchmark datasets which are the USPS for handwritten digits and the C-Cube for uppercase letters. The results indicate that tangent similarities allow a significant improvement in error rate when using 30 tangent vectors. Besides, it has been shown that N-SVM outperforms the OAA in both runtime and recognition accuracy.