-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Signal Processing
p-ISSN: 2165-9354 e-ISSN: 2165-9362
2011; 1(1): 24-33
doi: 10.5923/j.ajsp.20110101.05
Image Encryption and Decryption Using Chaotic Maps and Modular Arithmetic
S. Shyamsunder , Ganesan Kaliyaperumal
TIFAC-CORE in Automotive Infotronics, VIT University, Vellore, Pincode, 632014, India
Correspondence to: Ganesan Kaliyaperumal , TIFAC-CORE in Automotive Infotronics, VIT University, Vellore, Pincode, 632014, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper we have proposed a scheme which incorporates the concept of modular arithmetic and chaos theory, for image encryption and decryption. In the proposed scheme, we have used chaos theory to generate the necessary random matrix and used the same for Image encryption. For Decryption, we have used look-up table approach to find the element by element modular inverse of the random matrix and use it for decryption of an encrypted image. Our proposed scheme seems to be robust against various attacks.
Keywords: Logistic Map, Sine Map, Chebyshev Map, Modular Inverse, Look-Up-Table
Cite this paper: S. Shyamsunder , Ganesan Kaliyaperumal , "Image Encryption and Decryption Using Chaotic Maps and Modular Arithmetic", American Journal of Signal Processing, Vol. 1 No. 1, 2011, pp. 24-33. doi: 10.5923/j.ajsp.20110101.05.
Article Outline
1. Introduction
- In the past few years, the non-linear dynamics and chaos theory have gained a significant role in cryptography[1-9]. Cryptography is nothing but the study of hiding information. The aim of cryptography is to develop a cryptosystem that can transform the original data into a non-readable data. On decryption side, the cryptosystem should be able to convert the non-readable data into a readable form. Data can be of any form such as text, audio, video or else an image. Generally, we use cryptosystem for protecting our data against any unauthorised people. Hence, cryptography allows us protection against hackers and spies. Chaotic systems have high sensitivity to the initial conditions and parameters. If a slight change has been made in these parameters, the system will run into different orbits[9]. Hence it contains strong cryptographic properties. Hence we have considered chaotic system for the cryptography of an image. In this paper, we have combined modular arithmetic and chaotic system.The paper is organised as follows. In section 2, we discuss about modular multiplicative inverse. The proposed encryption scheme is explained in section 3. The decryption process is outlined in section 4. The observed experimental results are enumerated in section 5. Section 6 deals with security analysis and section 7 draws conclusions.
2. Modular Multiplicative Inverse
- In this paper, we have used the modular arithmetic for the proposed scheme. The modular multiplicative inverse of anumber is taken and stored in a look-up table. During decryption, this look up table is made use of. Let us now see what this modular multiplicative inverse is all about.In a set Zn, the two numbers a and b are multiplicative inverse of each other if
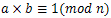 | (1) |
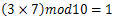 . It is possible to prove that a has a multiplicative inverse in Zn if gcd(n,a)=1. Whereaandn are said to be relatively prime.The Extended Euclidean algorithm can be used to find the multipicative inverse of b in Zn[10],[11]. Hence, using Extended Euclidean algorithm we calculate the inverse of a number and store it in a look-up table.
. It is possible to prove that a has a multiplicative inverse in Zn if gcd(n,a)=1. Whereaandn are said to be relatively prime.The Extended Euclidean algorithm can be used to find the multipicative inverse of b in Zn[10],[11]. Hence, using Extended Euclidean algorithm we calculate the inverse of a number and store it in a look-up table.3. Proposed Encryption Scheme
- We have proposed a chaotic cryptosystem and we have used three different maps (Logistic map[9], Chebyshev map[12] and Sine map). We have used modular multiplicative inverse and a look-up table for decryption.The equations of these maps are as follows:a) Logistic map
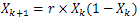 | (2) |
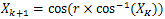 | (3) |
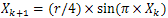 | (4) |
3.1. Present Proposed Scheme
- From the algorithms 1,2,and 3 shown below, we see that xx is the vector containing odd numbers and is generated using Logistic map-equation 2. xn1 is a matrix of size m n generated by converting a vector xx into a matrix. Then xn1 is multiplied element by element with the three image matrices (R,G,B). Hence, we get the R,G,B components of the encrypted colour Image.The algorithms 1,2and3 in the proposed Scheme use different chaotic maps:
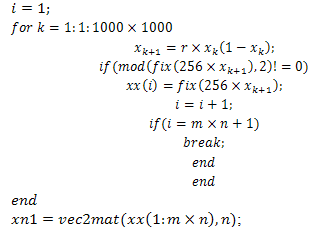 | Algorithm 1. The above algorithm is our proposed scheme using the Logistic map |
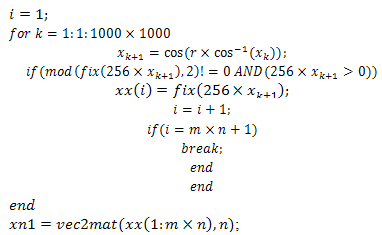 | Algorithm 2. The above algorithm is our proposed scheme using the Chebyshev map |
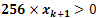 helps us to remove the negative numbers in our selection of positive odd numbers.
helps us to remove the negative numbers in our selection of positive odd numbers.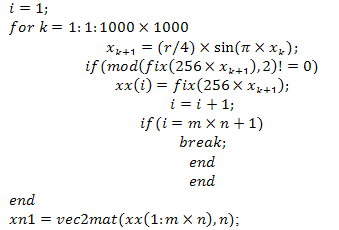 | Algorithm 3. The above algorithm is our proposed scheme using the Sine map |
4. Decryption
- The decryption is similar to encryption in terms of modular element by element multiplication. Since the decryption is an inverse process of encryption, we generate a matrix which contains element-wise modular multiplicative inverse of the random matrix used for encryption. In order to enhance decryption speed, we go for look-up table approach [14]. This look-up table contains the modular inverse of the odd numbers which lies in the same range as modulus 256.The Figure. 1below explains look-up table operation.
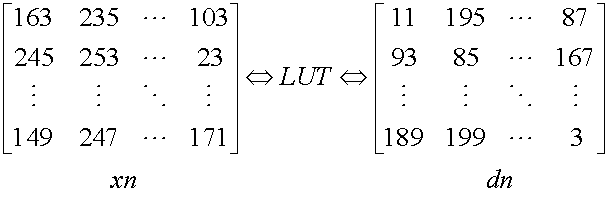 | Figure 1. The look-up table operation. |
5. Experimental Results
- In this section, we show the experimental results of our proposed scheme with different chaotic maps using a
 Lenna colour Image. Look-Up-Table concept in the proposed scheme makes the decryption time to be much faster. We shall see the time performance of our scheme with the corresponding chaotic maps in the next section 6.7. We have also carried out various attacks and the results are shown in the section 6. Our proposed scheme happens to be robust and faster when compared to the other schemes.The Figures. 2,3,4 are the experimental results of our proposed scheme. We have shown the encryption and decryption results.
Lenna colour Image. Look-Up-Table concept in the proposed scheme makes the decryption time to be much faster. We shall see the time performance of our scheme with the corresponding chaotic maps in the next section 6.7. We have also carried out various attacks and the results are shown in the section 6. Our proposed scheme happens to be robust and faster when compared to the other schemes.The Figures. 2,3,4 are the experimental results of our proposed scheme. We have shown the encryption and decryption results. | Figure 2. Encryption and decryption of the Image by our proposed Scheme using Logistic map. (a) Original Lenna Image, (b) Encrypted Lenna Image and (c) Decrypted Lenna Image. |
 | Figure 3. Encryption and decryption of the Image by our proposed Scheme using Chebyshev map. (a) Original Lenna Image, (b) Encrypted Lenna Image and (c) Decrypted Lenna Image. |
 | Figure 4. Encryption and decryption of the Image by our proposed Scheme using Sine map. (a) Original Lenna Image, (b) Encrypted Lenna Image and (c) Decrypted Lenna Image. |
6. Security Analysis
6.1. Key Space Analysis
- The robustness of a cryptosystem depends entirely on the secret keys. These secret keys must be very sensitive and the key space should be large enough so that the brute-force attacks will fail. The key space size tells us the number of different keys that can be used for the encryption of an image.In our experiment we have used 10-14precision[13]. We find that our proposed scheme is very sensitive to secret key mismatch. We have chosen the initial value of chaotic maps to be 0.20040226556816 having 10-14precision[13].We have generated keys using logistic map. If the precision is 10-14 then the size of the key space for initial condition is 2128. Hence the brute-force attack is difficult in our case.
6.2. Key Sensitivity Test
- The secret key for our proposed scheme is produced using the logistic map. Our image encryption process is sensitive to the secret key. When a change of 1 digit is made in the secret key, we get a completely a different encrypted image[15]. The following are the steps used to test the key sensitivity of our proposed scheme:
 is encrypted using the secret key 1489035384202401 and as a result we get an encrypted image 5(b).2. The same original image is then encrypted by changing the secret key by 1 digit i.e. 1489035384202402 and as a result we get an encrypted image 5(c).
is encrypted using the secret key 1489035384202401 and as a result we get an encrypted image 5(b).2. The same original image is then encrypted by changing the secret key by 1 digit i.e. 1489035384202402 and as a result we get an encrypted image 5(c).6.3. Histogram Analysis
- Histogram analysis is one of the security analysis which tells us the statistical properties of the ciphered image. Histogram of a ciphered image tells us how pixels in an image are distributed. It is done by plotting the number of pixels against the colour intensity levels[7,8,15]. In order to have a perfect ciphered image in terms of histogram, the histogram of the image must have uniform distribution of pixels against the colour intensity value. In our proposed scheme, we see that our method leads to this uniform distribution. Thus, our scheme do not provide any room for the statistical attacks.
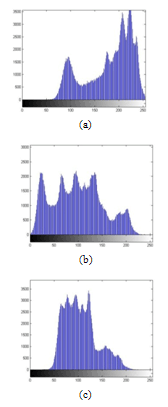 | Figure 11. Histograms of the original Image. (a) Histogram of red component, (b) Histogram of green component and (c) Histogram of blue component. |
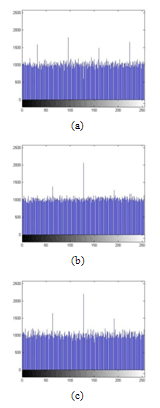 | Figure 12. Histograms of an encrypted image with Logistic map. (a) Histogram of red component, (b) Histogram of green component and (c) Histogram of blue component. |
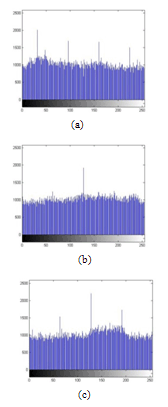 | Figure 13. Histograms of an encrypted image with Chebyshev map. (a) Histogram of red component, (b) Histogram of green component and (c) Histogram of blue component. |
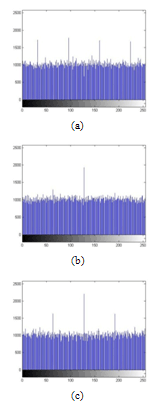 | Figure 14. Histograms of an encrypted image with Sine map. (a) Histogram of red component, (b) Histogram of green component and (c) Histogram of blue component. |
6.4. Correlation Coefficient Analysis
- Another type of statistical analysis is the correlation coefficient analysis. In this we analyse the correlation between two horizontally, vertically and diagonally adjacent pixels in the original Lenna image and its various encrypted images [7,8,15]. The Figure. 15tells us the correlation between two horizontally, vertically and diagonally adjacent pixels of the original image. We see that for the original image the adjacent pixels have high correlation (horizontally, vertically, and diagonally). We calculate the correlation coefficient using the following formulae:
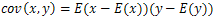 | (5) |
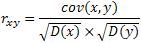 | (6) |
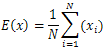 | (7) |
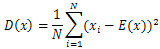 | (8) |
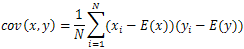 | (9) |
 image. We randomly choose 1000 pairs of two adjacent pixels (horizontal, vertical and diagonal) and plotted in a graph against each other. From Figures. 16 to 18, it is clear that there is a very negligible correlation between the two adjacent pixels in the encrypted images.
image. We randomly choose 1000 pairs of two adjacent pixels (horizontal, vertical and diagonal) and plotted in a graph against each other. From Figures. 16 to 18, it is clear that there is a very negligible correlation between the two adjacent pixels in the encrypted images.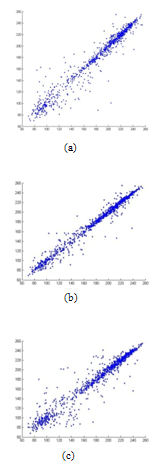 | Figure 15. Correlation analysis for the original image. (a) Correlation of two horizontally adjacent pixels, (b) Correlation of two vertically adjacent pixels, and (c) Correlation of two diagonally adjacent pixels. |
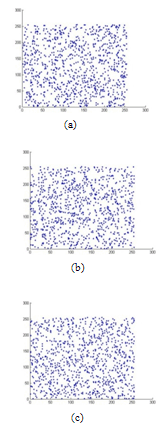 | Figure 16. Correlation analysis of the encrypted image with Logistic map. (a) Correlation of two horizontally adjacent pixels, (b) Correlation of two vertically adjacent pixels, and (c) Correlation of two diagonally adjacent pixels. |
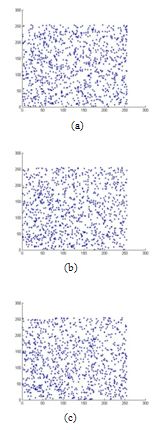 | Figure 17. Correlation analysis of the encrypted image with Chebyshev map. (a) Correlation of two horizontally adjacent pixels, (b) Correlation of two vertically adjacent pixels, and (c) Correlation of two diagonally adjacent pixels. |
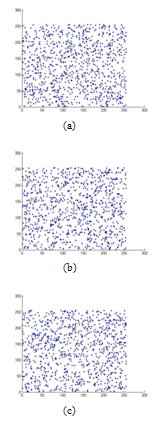 | Figure 18. Correlation analysis of the encrypted image with Sine map. (a) Correlation of two horizontally adjacent pixels, (b) Correlation of two vertically adjacent pixels, and (c) Correlation of two diagonally adjacent pixels. |
6.5. The Maximum Deviation Measuring Factor
- For measuring the quality of the encryption schemes, the maximum deviation measuring factor is used. This factor measures the deviation between the original image and the encrypted image[16]. The steps to measure this factor is as follows:1) First we count the number of pixels of each of grayscale value in the range between 0 and 255 for both original image and the encrypted image.2) Secondly, we calculate the absolute difference or else deviation between the original and encrypted image.3) Lastly, we count the area under the absolute difference. This is the sum of deviations (D) and this value represent the encrytpion quality. D is given as follows:
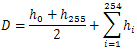 | (10) |
|
6.6. Chosen/Known-Plaintext Attack
- Chosen/Known-plaintext attack is one of the attacks where one can choose a set of plaintexts images and observe the corresponding cipher text images. In current era, this type of attacks occurs more frequently. In order for a ciphered image to be of highly secured, the security should be high against the known-plaintext and chosen plaintext attacks. The XOR-ing based techniques are not secured against these types of attacks. The system is not secured even when the secret key is changed for each plain text images[17]. We found out that our proposed scheme is robust against this kind of attacks.We shall now see how our scheme is secured against chosen/known-plaintext attack. Let us consider three
 images: I, I' and J'. Here I' is the encrypted image of the image I using a key k. J' is the another cipher text image which was encrypted using the same algorithm with the same key k. Im is the mask image which was obtained by XOR-ing the plaintext image I with its corresponding cipher text image I'. If we use the XOR-ing based techniques for encryption, then we can recover the unknown plaintext image J by XOR-ing the Im mask with the unknown cipher text image J' [17]. But our proposed schemes are very much robust that there is no scope of recovering the unknown plain text image J.If the encryption technique is XOR based then the recovery of unknown image J is possible[17]. This is done by the following equations:
images: I, I' and J'. Here I' is the encrypted image of the image I using a key k. J' is the another cipher text image which was encrypted using the same algorithm with the same key k. Im is the mask image which was obtained by XOR-ing the plaintext image I with its corresponding cipher text image I'. If we use the XOR-ing based techniques for encryption, then we can recover the unknown plaintext image J by XOR-ing the Im mask with the unknown cipher text image J' [17]. But our proposed schemes are very much robust that there is no scope of recovering the unknown plain text image J.If the encryption technique is XOR based then the recovery of unknown image J is possible[17]. This is done by the following equations: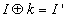 | (11) |
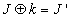 | (12) |
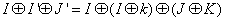 | (13) |
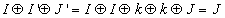 | (14) |
 | Figure 19. Chosen/known-plaintext attack for the Logistic map. (a) Original Lenna Image, (b) Encrypted Lenna Image, (c) XOR mask, (d) Unknown cipher-text ( the original image was “Baboon”), and (e) Failed attempt to crack the cipher image of “Baboon”. |
6.7. Speed Performance Analysis
- The security of the image is important but at the same time the speed of the proposed scheme is also important. The speed of an algorithm is one of the factors for a good encryption algorithm. We have measured the encryption and decryption time of our proposed scheme with the corresponding chaotic maps. The performance analysis was done on a computer having a specification as Intel(R) Core(TM)2 Duo CPU E7400 @2.80GHz 2.79GHz, 1.96 GB RAM. The average encryption/decryption time taken by the proposed scheme is done on
 image. The Table 3 shows the encryption and decryption time of our proposed scheme. By viewing the data, we see that the logistic map and our schemehas the least time and hence is the fastest of our proposed scheme with different chaotic maps.
image. The Table 3 shows the encryption and decryption time of our proposed scheme. By viewing the data, we see that the logistic map and our schemehas the least time and hence is the fastest of our proposed scheme with different chaotic maps. | Figure 20. Chosen/known-plaintext attack for the Chebyshev map. (a) Original Lenna Image, (b) Encrypted Lenna Image, (c) XOR mask, (d) Unknown cipher-text ( the original image was “Baboon”), and (e) Failed attempt to crack the cipher image of “Baboon”. |
 | Figure 21. Chosen/known-plaintext attack for the Sine map. (a) Original Lenna Image, (b) Encrypted Lenna Image, (c) XOR mask, (d) Unknown cipher-text ( the original image was “Baboon”), and (e) Failed attempt to crack the cipher image of “Baboon”. |
|
7. Conclusions
- In this paper, we have proposed encryption and decryption of an image using chaotic maps and modular arithmetic. We have dealt with three different combinations of our proposed scheme. We have made use of look-up table for faster decryption process. One of the best features of our algorithm is the simplicity as well as speed. Our proposed scheme is also robust against many attacks.In a chaos-based encryption algorithm, the relationship between one pixel and another pixel is very negligible or else nil. Our proposed scheme also depicts this property.Out of the three different maps used, we find that the logistic map is the fastest of all and hence is considered to be the best algorithm for encryption and decryption.
ACKNOWLEDGEMENTS
- The authors of this paper would like to acknowledge the Department of Science and Technology, India for their support and for the financial assistance provided for this work. This work is a part of “Chaos based Security systems in Transform Domains” project funded by DST (Department of Science and Technology) through the grant number: SR/S2/HEP-16/2009 dated 15th Jan 2010.
References
| [1] | L. M. Pecora and T. L. Carroll, “Synchronization in chaotic systems”, Phys. Rev. Lett. 64, pp. 821-824, 1990 |
| [2] | L. Kocarev, M. Sterjev, A. Fekete, and G. Vattay, “Public-key encryption with chaos”, Chaos 14, pp. 1078-1082, 2004 |
| [3] | S. H. Wang, J. Y. Kuang, J. H. Li, Y. L. Luo, H. P. Lu, and G. Hu, “Chaos-based secure communications in a large community”, Phys. Rev. E 66, 065202, 2002 |
| [4] | H. P. Lu, S. H. Wang, X. W. Li, G. N. Tang, J. Y. Kuang, W. P. Ye, and G. Hu, “A new spatiotemporally chaotic cryptosystem and its security and performance analyses”, Chaos 14, pp. 617-629, 2004 |
| [5] | X. G. Wang, M. Zhan, C.-H. Lai, and G. Hu, “Error function attack of chaos synchronization based encryption schemes”, Chaos 14, pp. 128–137, 2004 |
| [6] | X. G. Wang, X. F. Gong, M. Zhan, and C.-H. Lai, “Public-key encryption based on generalized synchronization of coupled map lattices”, Chaos 15, 023109, 2005 |
| [7] | Zhang Yong, “Image Encryption with Logistic Map and Cheat Image”, International Conference on Computer Research and Development, pp. 97-101, March 2011 |
| [8] | RashidahKadir, RosdianaShahril, and MohdAizainiMaarof, “A modified image encryption scheme based on 2D chaotic map”, International Conference on Computer and Communication Engineering, pp. 1-5, May 2010 |
| [9] | M.Lakshmanan, and S.Rajasekar, “Nonlinear Dynamics: Integrability, Chaos, and Patterns”, Springer- Verlag Berlin Heidelberg, 2003 |
| [10] | William Stallings, “Cryptography and Network Security”, Prentice-Hall of India, Fourth edition, 2006 |
| [11] | Behrouz A. Forouzan, “Cryptography and Network Security”, Tata McGraw-Hill, Special Indian Edition 2007 |
| [12] | K. Ganesan, Ishan Singh, and MansiNarain, “Public Key Encryption of Images and Videos in Real Time Using Chebyshev Maps”, Fifth International Conference on Computer Graphics, Imaging and Visualization, pp. 211-216, 26-28 August 2008 |
| [13] | FangjunHuang ,Zhi-Hong Guan, “Cryptosystem using chaotic keys”, Chaos, Solitons and Fractals, 23, pp.851-855, 2005 |
| [14] | K.Ganesan, R.Muthukumar, K.Murali, “Look-up Table Based Chaotic Encryption of Audio Files”,IEEE Trans. CircSyst 2006, APCCAS 2006, pp. 1951-1954, 2006 |
| [15] | N.K. Pareek, VinodPatidar, K.K. Sud, “Image encryption using chaotic logistic map”, ScienceDirect, Image and Vision Computing, Volume 24, Issue 9, pp.926-934, 1 September 2006 |
| [16] | Nawal El-Fishawy and Osama M. Abu Zaid, “Quality of Encryption Measurement of Bitmap Images with RC6, MRC6, and Rijndael Block Cipher Algorithms”, International Journal of Network Security, Volume 5, No.3, pp. 241–251, November2007 |
| [17] | Daniel Socek, Shujun Li, Spyros S. Magliveras and BorkoFurht, “Enhanced 1-D Chaotic Key-Based Algorithm for Image Encryption”, IEEE International conference on security and privacy for emerging areas in communication, pp. 406-407, Sep2005 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML




