1. Introduction

Bsplines have been long introduced and analyzed by[1], due to their merits of being flexible and provide a large degree of differentiability and cost/quality trade off relationship. By changing the Bspline function order we move from a linear representation to a high order band limited signal form. Bsplines have been utilized by[3,4] and[9] as a powerful image registration, classification and feature extraction tool. However they have not been investigated for image coding and compression applications, due to the fact that they are not fully orthogonal basis. Bspline wavelets are well known of being orthogonal across time shifts, but not across time scale[3]. It’s our belief that this distinctive decomposition feature décorrelates/removes some data redundancy that is not removed by regular orthogonal basis (e.g. DCT or Wavelet basis).

In this paper, we propose to improve the compression performance of several well known wavelet based image coders by preprocessing the image first through Bspline decomposition. This would further reduce the data correlation and would achieve better compression performance as evident by our adopted correlation measure[6] with and without the proposed technique and by the enhanced PSNR/bpp curves. We derive our Eigen analysis theoretic justification for this compression enhancement.

In this paper we also propose a novel implementation technique for the Bspline coefficient calculation. This technique is based on a straight forward calculation approach through a Toeplitz matrix that allows parallel calculations for online applications. Moreover it guarantees that the length of the output signal is exactly equal to the input batch length, to avoid any extra samples overlaps. Input coefficients can be handled simultaneously to calculate a Toeplitz matrix that can calculate the Bspline signal coefficients. The proposed technique can take blocks or vectors of input samples or batches, which make it more suitable for video/image manipulation online applications.

Bsplines are known to be integer coefficients and representations as they are the exact mathematical translators between the discrete and continuous versions of signals. The proposed Toeplitz matrix technique preserves the integer status of the coefficients and allows an exact interpolation process. This Toeplitz matrix also guarantees that the length of the output signal is to be exactly equal to the input batch length in a regular transformation process, to avoid any extra samples overlaps. This makes it more suitable for several image/video applications, where data is partitioned into non overlapping blocks for processing and manipulation.

Section 2 gives some background about the Bspline basis reconstruction. Section 3 shows our straight forward approach of calculation of the Bspline basis along with our Eigen analysis justification for compression enhancement and our adopted correlation measure[6]. Section 4 shows our proposed implementation approach of these Bspline basis. Section 5 shows our extensive simulation results for Eigen analysis comparison of Bsplines with different orders with DCT. It also compares the correlation measure of the data with and without Bspline preprocessing. It also illustrates different PSNR versus bpp curves for the SPIHT image coder with and without the proposed Bspline preprocessing approach. Complexity analysis on a hardware platform (DSK 6713 Digital Signal Processor) for both the proposed technique and traditional implementation[1] are also proposed in section 5. Discussion and conclusions are in sections 6 and 7, respectively. Some of the work in this paper has been previously reported in [12]

2. Background

2.1. Mathematical Background

The m^th order Bspline function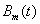, satisfies the following basic properties:

1. 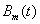is of finite support and equals zeros at t0 and tm. Between the knots t = 1,2,..,m-1, it is represented by a polynomials of order (m-1) in t. It satisfies the recurrence relation:

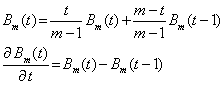(1)

2. The Fourier transform is given by

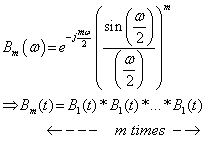(2)

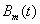is symmetric about 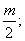i.e.

(3)

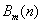The discrete B-spline is obtained by sampling 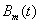at its knots t=0,1,..,m. The L^th interpolated discrete Bspline is obtained by sub-sampling the sampling interval into L equal intervals i.e..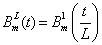

2.2. Signal Construction Using Bsplines

For a discrete signal g(k) of length N, that is interpolated using an m^th order discrete Bspline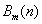, we would have

(4)

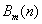Where c(l)’s are the Bspline decomposition basis for the g(k) signal. The limits in 4 are due to the nonzero values of, This means that a batch of length N can be expanded by Bspline polynomial having an utmost N+m-2 coefficients.

3. Proposed Bspline Calculation Approach

The previous algorithm of calculating the Bspline basis[1](Fig 1 and Fig 2) mainly generates extra output samples (m samples for N input samples interpolated with a Bspline of order m). It also takes one input sample on the spot. In this section we proposed our new methodology of Bspline basis calculations using a batch of input samples without any extra output samples.

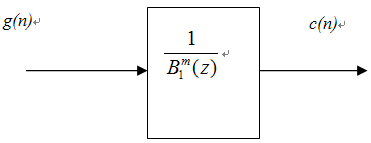Figure 1. Viewing the interpolation process as a filtering operation.

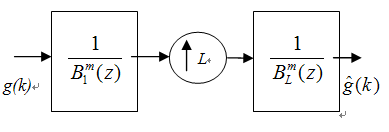Figure 2. Viewing B-spline interpolation as a multirate filter.

We can compute the C’s if the limits of eqn. 4, is changed to

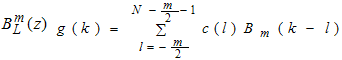(5)

Then only N coefficients are needed. The C’s are solution of the linear system

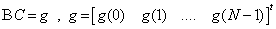The solution of this system is much simpler. In case of cubic Bspline, the matrix is B reduces to Tri-diagonal matrix, whose solution is straight forward and can be implemented online, unlike the original computationally expensive approach in[1].

(6)

, where B is NxN matrix

3.1. Bspline Based Compression

It is well known from the transform theory basics that the efficiency of any transformation would depend on the amount of data décorrelation and energy concentration it offers. To measure the energy concentration for a transformation (with natural images) we calculate the covariance matrix for any natural image (which can be modelled by an AR(1) with [8]). The covariance matrix can be:

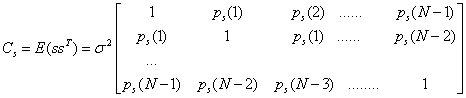Where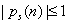,[8]. The covariance matrix of any transform coefficients can be calculated as:

, where 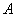represents the transform basis (for DCT, Bsplines, wavelets…). The Eigen values of the covariance matrix represent the amount of energy concentration in the transformation. It can be shown in Fig. 3 that the Eigen values for the Bspline basis are higher (for the first few values) than the DCT basis. However after a few Eigen values it drops for the Bspline basis and it goes below the DCT ones. This justifies the improvement of energy concentration for the Bspline basis over the DCT basis for low bit rates (less than 1 bpp). Fig. 3 shows the Eigen values of the Bspline basis for different orders in comparison with the DCT basis. It can be shown that the higher is the Bspline basis the more energy concentrated it would be over the DCT, however it takes more time in calculating the Bspline basis (B matrix) as in the previous section.

Figure 3. Comparison of the Eigen values of DCT Basis with Bsplines Cubic, Quadratic, and order 5.

In[6] a new methodology has been presented for correlation calculation. It has been shown that the degree of decorrelation would increase with the increase of the slope between the diagonal elements and the second off diagonal elements as well known from basic information theories. It has also been reported in[6] that for a normalized basis tri-diagonal matrix (which represent the cubic Bspline in our calculations) as in eq.7, the less the value of alpha, the better is the degree of decorrelation. This value was also consistent with regular decorrlation measures reported in[8], which compares the nondiagonal matrix entries before and after the transformation. We performed the same measure on our proposed system by calculating the alpha for the image wavelet coefficients with and without the proposed Bspline based preprocessing correlation removal technique as in table 1. This alpha represents the slope of the diagonal decay in the basis matrix as in eq.7.

(7)

In our proposed system, we decompose the image first through the Bspline basis block. Where the image Bspline basis (C’s from eq. 4) are calculated (with separability) and sent to the image coder instead of the actual image pixels that are fed to the coder normally.

For every 8x8 block, a 8x8 block of C’s is calculated using the B matrix as in eq.6. The resulting 8x8 block of basis has a lower degree of correlation. We can then use the C’s for either Block based compression (eg. DCT) or sub-band based compression (eg. Wavelets). We note here that the cubic Bspline (3^rd order) basis was used in most of our experiments as it gives the best complexity/accuracy trade off[1].

4. Proposed Basis Implementation

4.1. Integer Representation for Cubic Bspline

For an integer cubic Bspline, the value of 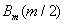is 2/3, and. For BC = G, a cubic tri diagonal matrix can be represented as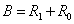

, where

(8)

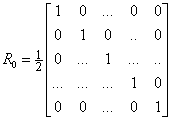(9)

For the C vector to be multiplied by the single diagonal of, the result would be the same as vector C. so G = C.

For the C vector to be multiplied by the three diagonals of , the result would be as follows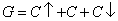

, where the arrow indicates a shift up or down of input C vector (with no rotate). This is due to the fact that

(10)

where matrix[C] is dot multiplied by the one’s and zero’s matrix. Since it is sought to calculate the C’s values, given the G, then the ½ and 1/6 factors, would be flipped at the other side of the equation and would be like multiplying by 2 or 6, which could be easily implemented with a few shifters and adders.

We note here that the Bspline factors are all integer or fraction of integers, which eliminates any chance of a floating point number that would involve a multiplier or divider.

4.2. General Implementation for Bspline Bases matrix

The B matrix for calculating the Bspline Basis could be generalized to be

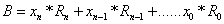(11)

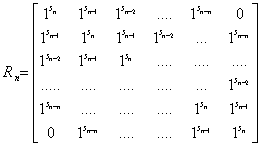(12)

So if we are dealing with a bilinear Bspline (order 2), there will be only one R matrix with only one diagonal that is non zero. If we have a cubic Bspline (order 3) as in section 3, then we would have two R matrices, the first with 3 diagonals that are non zeros and the second with one diagonal that is non zero. If we are dealing with an mth order Bspline, we would have m-1 matrices. The first with (((m-2)*2)+1) non zero diagonals, the second with (((m-3)*2)+1) non zero diagonals and finally the (m-1) matrix with one non zero diagonal.

In all R matrices, any non zero element must take a value of one. The size of the R or B matrix, would depend on the length of the input batch of samples that we need to calculate the (integer) Bspline basis for. The coefficients xn are integer Bspline factors originally proposed in[1].

Following the derivation of eq. 10, for a vector C to be multiplied by a matrix with five diagonal non zero elements, (Quadratic Bspline of order 4), the output would be according to this equation

Where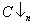, corresponds to shift down n times, and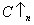, corresponds to shift up n times.

For a matrix with (((m-2)*2) +1) diagonals that is multiplied with C, the output would be

Hence the full implementation can be performed with only adders and shifters[11].

5. Experimental Results

Several simulation results has been carried out on our proposed Bspline based image coding technique. For every 256x256 image we first calculate the 8x8 Bspline basis (C’s) for the image and then we send these basis to be coded through the regular SPIHT coder[10]. We compared the compression performance of this proposed approach with the regular compression approach which doesn’t include calculating the Bspline basis. For low bits per pixels we found that our proposed approach gives substantial improved PSNR/bpp curves as shown in fig 4,5,6. Table 1 shows the amount of time needed for MATLAB simulations with and without the Bspline (Cubic) basis calculation along with the alpha values in eq.7 for both cases. Fig.3 compares the Eigen values of Bsplines with DCT for different orders, Cubic, Quadratic, and order 5. As shown in the table, the proposed redundancy removal procedure doesn’t require much complexity in terms of simulation time and has reduced correlation. It is shown (Fig. 3), that higher Bspline orders is better when compared to DCT, but with extra complexity.

Table 1. Complexity of the Bspline-SPIHT coder and correlation measure for the C’s and pixels Image (256x256) Encoding Time with Bspline Alpha for the C’s Encoding Time without Alpha for the original pixels Lena 30ms 0.24 25ms 0.4 Cameraman 32 ms 0.27 27ms 0.32 Mandril 29 0.29 24ms 0.36

The proposed Bspline basis calculation approach was implemented on Digital Signal Processor (DSK 6713). Table 2, compared the proposed calculation approach with different input batch length. We also list the time needed for the proposed approach versus the original calculation method first proposed in[1] and[3] but on MATLAB only. This is due to the fact that original Bspline calculation methodology is computationally expensive and inefficient to implement on a hardware platform.

Table 2. Implementation complexity analysis of Bsplines method order Batch length Time Matlab No of cycle on a DSK Proposed 3 1 12ms 23ms Proposed 3 8 18ms 26ms Proposed 4 8 19ms 25ms Original[1] 3 1 19ms N/A

Fig. 4 shows a sample image after using the proposed calculation approach for zooming. It gives identical results to the original Bspline calculation method in[1].

Figure 4. Visual sample for our enhanced technique.

Figure 5. Rate Distortion of Lena image.

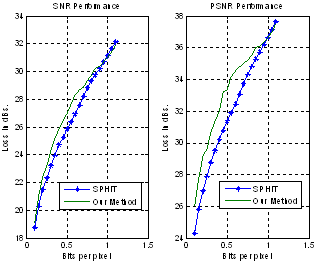Figure 6. Rate Distortion of Cameraman image.

6. Discussion

We note here that our improved results are mainly due the distinctive feature of the Bspline basis that has a large amount of energy concentration with low spatial frequencies. This justifies the improved PSNR for low bit rate. As shown in Fig. 3, after a certain threshold bit rate, the energy concentration drops below DCT and the image gets further deteriorated in spite of the increased bit rate. We note here that the amount of compression performance enhancement would be best with the cubic Bspline and would mainly depend upon the image content. Orthogonal decomposition is still needed to code the Bspline basis for full orthogonality.

7. Conclusions

In this paper a Bspline based image coding technique was presented that mainly depends on Bsplines in some redundancy removal prior the regular decomposition or/and compression process in any image coder. We also presented an efficient implementation for this coding methodology.

ACKNOWLEDGEMENTS

This work is funded from the Alexander von Humboldt foundation, Germany.