-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2023; 13(1): 8-12
doi:10.5923/j.ajor.20231301.02
Received: Jul. 1, 2023; Accepted: Jul. 17, 2023; Published: Jul. 24, 2023

Multi Floor Unequal Area (Machine and Slots) Facility Layout Problem (MF-UA-FLP)
RRK Sharma1, Vinay Singh2, Kshitiz Mittal3, Didigam Nithin4
1Dept of IME, IIT Kanpur, 208016, India
2ABV-IIITM Gwalior, India
3UG Student, Dept of ChE, IIT Kanpur, 208016, India
4UG Student, Dept of MSE, IIT Kanpur, 208016, India
Correspondence to: RRK Sharma, Dept of IME, IIT Kanpur, 208016, India.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

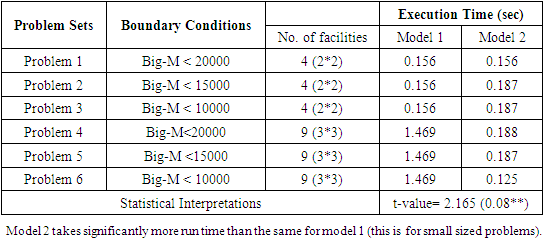
In this paper we model unequal sized area and machines problem in a multi floor context. We define a constant that is 1 if facility fits into a slot and 0 otherwise; and model the problem to min material handling cost (model 1). Later we prepare a new model (model 2) that minimizes sum of material handling cost and the fitness cost (that puts good fitness is one and poorest fitness is 10; and no fit at BIG_M which is a real number much larger than largest positive constants of the problem). We add additional fitness cost in model 2 and it is optimised. Material handling cost (MHC) in model 1 is significantly lower in problems of size equal to 9 (no of facilities) than MHC in model 2; MHC is lower (not significantly) in model 1 than in model 2 for problem of size 25 and MHC is lower in model 2 than in model 1 (not statistically significant) for problem size of 81. Model 2 has less number of constraints than the model 1 and takes less RUN TIME (not statistically significant for facilities equal to 9 and statistically significant for facilities of sizes 25 and 81). Detailed computational performance of these two models is given (6 small sized problems; and 15 problems each of size (facilities equal to) 9, 25 and 91).
Keywords: Multi-Storey Facility Layout, Facility Layout Problem with Unequal Sized Slots and Facilities
Cite this paper: RRK Sharma, Vinay Singh, Kshitiz Mittal, Didigam Nithin, Multi Floor Unequal Area (Machine and Slots) Facility Layout Problem (MF-UA-FLP), American Journal of Operational Research, Vol. 13 No. 1, 2023, pp. 8-12. doi: 10.5923/j.ajor.20231301.02.
Article Outline
1. Introduction of Multi-Floor Facility Layout Problem
- The Facility Layout Problems (FLPs) in literature have the following properties: (1) the departments have different areas and, (2) the facility can be one-, two-, or three-dimensional. The different dimensions lead to the three broad classes of FLPs covered in literature, namely row FLPs, unequal-areas FLPs, and multi-floor FLPs. One-dimensional facilities lead to row FLPs, and we categorize them in terms of the number of rows: single-row, double-row, or multi-row. Single-row and double-row problems commonly occur in practical applications. Multi-row problems are a natural extension of the problem to three or more rows. Unequal-areas FLPs have two-dimensional facilities with a single floor. Three-dimensional facilities give rise to multi-floor FLPs in which departments are to be placed over two or more floors. Most of the literature proposes models for specific applications rather than for the general problem. Unequal-areas FLPs have two-D machines on a single floor, and it is assumed in literature that the machine is Square/rectangular and that all machines fit inside the floor. Three-dimensional facilities give rise to multi-floor FLPs in which departments are to be placed over two or more floors. Most of the literature proposes models for specific applications rather than for the general problem. In literature Unequal-areas FLPs is formulated as Quadratic Assignment Problem (QAP). The objective in QAP formulation is to minimize material handling cost, which is the multiplication of flow frequency between departments and corresponding rectilinear distance between departments. The Unequal-Areas FLP (UA-FLP) is concerned with finding the optimal arrangement of a given number of non-overlapping indivisible departments with varying areas so as to minimize the total expected cost of flows inside the shop. The UA-FLP, sometimes called the single-floor FLP, has received much attention in the literature. It was first stated in Armour and Buffa (1963), and one of the first MILP formulations was proposed in Montreuil (1991) using binary variables to prevent overlap. The UA-FLP is an NP-hard optimization problem in which exact techniques do not obtain good results. Thus, it has been successfully dealt with different heuristics and meta-heuristics in the past. Recently Garcia-H et al. (2020) addressed the UA-FLP with a multi-method ensemble approach, the Coral Reefs Optimization algorithm with Substrate Layers (CRO-SL). In literature, researchers have given Exact Formulation of UA-FLP (Van Camp et al. (1991))), MILP (Mixed Integer Linear Optimization) approaches introduced by Meller et al. (1999) and enhanced in Sherali et al. (2003). These all are continuous formulations. As far as our knowledge, no researcher has so far given discrete formulation for UA-FLP. Matai et al 2021 gave first discrete formulation of UA-FLP. To our knowledge no one has given discrete formulation of MF-UA-FLP which is hybrid in nature that covers the problem edge of unequal-area FLPs and multi-storey FLPs. Several models on facility layout can be found in Sharma (2019, 2019, 2020, 2020, 2021 and 2022). In the next section we give two new discrete formulations of problem MF-UA-FLP. Problem FormulationThe problem is to build a model to find the optimal cost that minimises the below equation using the minimisation algorithm, given the distance between the slots. This is done by using GAMS software.Constants: R(f,F,s): ‘1’ if facility ‘f’ fits into slot ‘s’ at floor ‘F’ and ‘0’ otherwise. FL(f1,f2): Flow between facility ‘f1’ and ‘f2’. D(F1,s1,F2,s2): Distance between slots s1 and s2 that are respectively on floors F1 and F2. Decision Variable: X(f,F,s): ‘1’ if facility ‘f’ is assigned to k th slot on floor ‘F’ and ‘0’ otherwise. Model 1:
 In model 1 we minimize the material handling cost (equation (1)). Equations (2) ensure that a facility gets into exactly one slot; and equations (3) ensure that one slot gets exactly one facility. Equation (5) ensure that a facility gets into at least one slot (which is legally possible) and equations (6) ensure that a a slot gets at least one facility that is legally permissible. Model 2:We can add fitness cost very easily to this formulation. This prevents very small facilities to be located in large slots as far as possible. An alternate formulation to Model 1 (min (1) st (ii) to (vi) can be given as Model 2 below. Define FIT_Cost(f,F,s): ‘BiG-M’ if facility ‘f’ does not fit into slot ‘s’ at floor ‘F’ and some number between 1 and 10 otherwise; (higher number denotes poor fit and lower numbers denote good fit).
In model 1 we minimize the material handling cost (equation (1)). Equations (2) ensure that a facility gets into exactly one slot; and equations (3) ensure that one slot gets exactly one facility. Equation (5) ensure that a facility gets into at least one slot (which is legally possible) and equations (6) ensure that a a slot gets at least one facility that is legally permissible. Model 2:We can add fitness cost very easily to this formulation. This prevents very small facilities to be located in large slots as far as possible. An alternate formulation to Model 1 (min (1) st (ii) to (vi) can be given as Model 2 below. Define FIT_Cost(f,F,s): ‘BiG-M’ if facility ‘f’ does not fit into slot ‘s’ at floor ‘F’ and some number between 1 and 10 otherwise; (higher number denotes poor fit and lower numbers denote good fit). 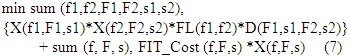 s.t. (2) to (4). In model 2 we avoid a bad fit by assigning higher FIT_Cost values (1 for good fit and 10 for bad fit: wherever R(f1,F1,s1) = 1; and assign FIT_Cost = BiG_M wherever R(f1,F!,s1) = 0). In model 1 fitness is either 1 or 0 (it is either fit or unfit). In Model 2 constraints (5) and (6) are eliminated. It can make formulation of Model 2 more efficient than formulation of Model 1 as now we have to process few numbers of constraints. The empirical investigation of the formulation is presented in next section.
s.t. (2) to (4). In model 2 we avoid a bad fit by assigning higher FIT_Cost values (1 for good fit and 10 for bad fit: wherever R(f1,F1,s1) = 1; and assign FIT_Cost = BiG_M wherever R(f1,F!,s1) = 0). In model 1 fitness is either 1 or 0 (it is either fit or unfit). In Model 2 constraints (5) and (6) are eliminated. It can make formulation of Model 2 more efficient than formulation of Model 1 as now we have to process few numbers of constraints. The empirical investigation of the formulation is presented in next section.2. Empirical Investigation
- The model 1 and 2 were coded in the GAMS package (refer Annexure-I for the codes of Model 1 and Model 2). The six problems were fed to the program and the results are reported in the table 1. Model I was solved using mixed integer quadratic constrained problem (MIQCP) method by Min (1), s.t. (i) to (vi). While Model II was solved using MIQCP with the summation of FIT_Cost added as Min (7), s.t.(2) to (4).It is now easy to see that model 1 (min (1) s.t. (2) to (6)) is equivalent to model 2. In model 2 constraints (5) and (6) are eliminated. It may make formulation 2 more efficient than formulation 1 as now we have to process few numbers of constraints. We compare optimal objective values of two approaches (Model 1 and Model 2) and respective CPU times.
|
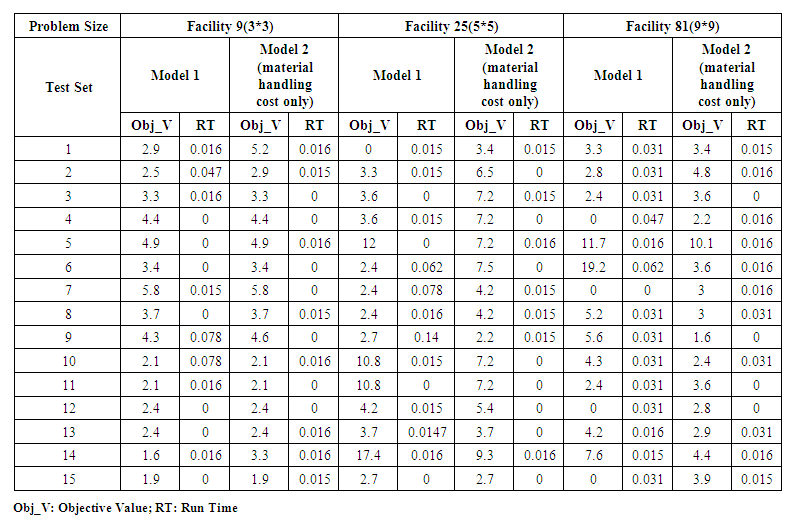 | Table 2. Comparative Results of Model 1 and Model 2 (material handling cost only) |
|
3. Results and Conclusions
- Based on the pilot observations of solutions derived by running 06 problems execution time on a common computing machine with technical specification as Intel i7, 3.8 GHz, and 4GB RAM, the Modified Model 2 is performing better than Model 1 to deliver appropriate objective values and with lower execution time (statistically significant for number of facility equal to 25 and 81). MHC for model 1 is less (but not significant) than MHC for model 2 (for facility equal to 9 and 25); and MHC for model 2 is less (but not significant) than MHC for model 1 for facility equal to 81. We thus gave 2 new models for multi floor SPLP with unequal machine and slot sizes and shown that model 2 takes significantly less run time. This is a useful contribution of this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML