1. Introduction

The transportation problem (TP) is a special class of linear programming problems, which deals with shipping commodities from sources to destinations. The transportation problem is to find the amount of commodity which should be transported from each source to each destination satisfying all the supply and demand limits of sources and destinations respectively so that the overall transporting cost is minimum which the objective of the TP. If the total supply and demand limits are equal, then the problem is said to be a balanced transportation problem with equality constraints.

The transportation problem was formalized by the French Mathematician Monge, [1]. Major advances were made in the field during World War II by the Russian Mathematician and Economist Leonid Vitaliyevich Kantorovich [2]. The standard form of the transportation problem was first presented by Frank Lauren Hitchcock [3]. Efficient methods of solution were derived by T. C. Koopman [4], Dantzig, G.B., [5], and then by Charnes A. et al. [6-8].

Many researchers developed a lot of methods to solve the Transportation problem. Some recent research work I mentioned here. Babu et al. [9] demonstrate that Vogel’s Approximation Method (VAM) has some limitations and computational blunders. To overcome these limitations, they developed an Improved Vogel’s Approximation Method (IVAM) by correcting these blunders.

Baidya [10] develop the stochastic solid transportation models to minimize the total transport time and ensuring safety with the safety and time objective functions. Dash and Mohanty et al. [11] inspect the TP where unit transportation cost, supplies, and demands are measured as uncertain normal variables. They develop the conceptual uncertain programming model for TP which is converted to a deterministic linear programming model. Sometimes per unit transport cost is uncertain due to the unstable condition of the fuel market. Gupta and Arora [12] provide an algorithm for determining the minimum unit transportation cost in a capacitated transportation problem with bounds on rim conditions. Ahmad and Adhami [13] develop a couple of mathematical optimization models to obtain the lower and upper bounds of the TP, where the supplies and demands quantities vary in an interval. Some transport systems impose a certain charge to use their routes along with the transport cost. Khurana and Adlakha [14] propose an algorithm for solving a multi-index fixed charge bi-criterion TP which minimizes the variable and fixed costs simultaneously to yield an optimal basic feasible solution. They also offer an algorithm to obtain an initial basic feasible solution of the multi-index TP.

If the capability of a supply is appreciably expanded/reduced and the requirement of a destination is also appreciably expanded/decreased, then the usual transportation system transformed to unequal transportation problem with mixed constraints. The special type of transportation problem with mixed constraints was meticulously studied firstly by Brigden [15]. He solved this problem by considering a related standard transportation problem having two additional sources and two additional destinations. Klingman, D., et al. [16-18] in transportation problem with mixed constraints interpret generalization of standard transportation problem having only one additional origin and destination. They accommodate the mixed transportation model by showing that it is equivalent to a standard transportation problem having only one additional origin and destination whereas Isermann, H. [19] in his paper show that to each transportation problem with mixed constraints a standard transportation problem with two additional costs can be related. Very few researchers published their research work on transportation problems with mixed constraints. Some well-known and existing methods are- LBP (least bound problem) proposed by Veena Adlakha, et al. [20] state that LBP is obtained by changing all inequalities to equalities with the lowest possible feasible right-hand side values. Then balanced it by using VAM and solve it with any transportation algorithm. Place the load(s) of the dummy row(s)/ column(s) of the balanced LBP at the lowest cost feasible cells of the given TP to obtain a solution for the TP with mixed constraints. Then Pandian, P. et al. [21-23] introduced a method named Zero Point Method, Fourier method, more for solution for fuzzy transportation problem for finding an optimal solution of mixed constraints transportation problem. Mondal R.N. et al. [24] developed new algorithms to find an optimal solution by using computer programming for TPs with mixed constraints. Also Arora and Khurana [25-26], Adlakha et al. [27-32], Pandian, P. et al. [33] Arsham, Gani, A. et al. [34], Akilbasha, A. et al. [35] Rayan, M. [36] proposed some algorithm has demonstrated the identifying cases where MFL paradoxical situation exists and also has provided various methods for finding MFL solution for transportation problems. Gupta, S. et al. [37] explain multi-objective capacitated transportation problem with mixed constraints. Agarwal et al. [38]. developed minimax method for Time minimizing transportation problem with mixed constrain. P. Rajarajeswari and D. Maheswari [39] presented Transportation problem with mixed constraints having all parameters as integer intervals is considered. Here we solve the fully integer interval transportation problem without converting it to the crisp transportation problem. Three Dimensional Bounded Transportation Problem by Kavita Gupta and Ritu Arora [40] presents a methodology to solve a three dimensional bounded transportation problem. Bounded transportation problem is expounded by defining a parallel bounded transportation problem. Equivalence between the two problems is established. A method has been developed for finding an optimal more-for-less solution in transportation problem by Nikky Kumari [41]. Khoso, A. M. et al. [42] proposed Modified LCM’s Approximation Algorithm for Solving Transportation Problems has been developed in order to gain foremost fundamental capable solution of transportation issues where entity cut down the transportation expensive. The proposed algorithm is correlate with popular presenting methods corralling NWCM, LCM. Gupta, G., Rani, D., & Singh, S. [43] considered transportation problems with uncertainty in transportation costs and proposed an alternate algorithm to find its initial basic feasible solution. The grade value for the zero costs is defined and is used to find the initial solution. Numerical examples with transportation costs represented by different kinds of fuzzy numbers have been added to illustrate the proposed methodology. The paper discussed a solution procedure of a multi-objective capacitated transportation problem (MOCTP) in an uncertain environment by Gupta, S., Ali, I., & Chaudhary, S. [44].

A literature search uncovered that much effort has been focused on classical transportation problem with equality constraints which is computationally easy to solve. Very few numbers of papers observed in the literature address the transportation problem with mixed constraints. In our proposed method we solve the transportation problem with mixed constraints by adding one additional row and a column. Then step by step complete the total procedure. Our method is easy to understand gives a better result than another existing method. Then we provide a table showing the comparison of some existing methods and the proposed method. we proposed only the solution procedure of transportation problem with mixed constraints without touching MFL paradoxical situation.

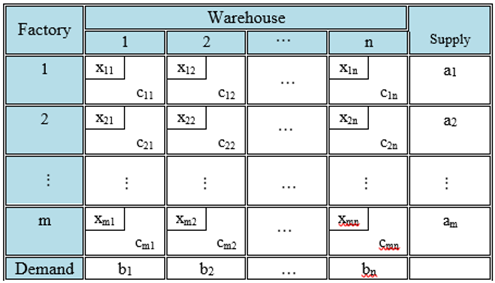
2. Formulation of a General Transportation Problem

A set of m supply points (origins) O₁, O₂, … …, O_i, … …, O_m from which a good is shipped. The supply point i can supply at most a_i units. A set of n demand points (destinations) D₁, D₂, … …, D_j, … …, D_n to which the good is shipped. Demand point j must receive at least b_j units of shipped goods. c_ij is the unit transportation cost and x_ij is the amount of product transported from sources i destinations j.

Using the above notation, the general transportation problem can be represented by the network diagram shown in Fig-1:

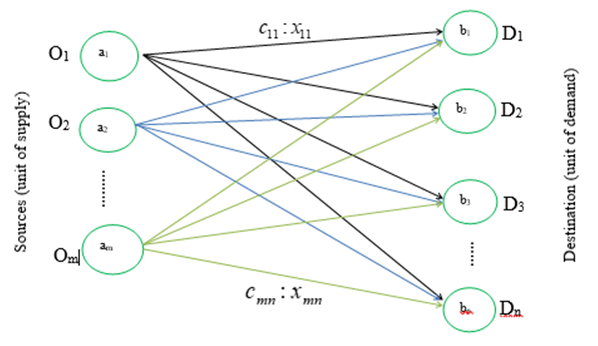Figure 1. Network Representation of Transportation Problem

We can also represent the TP by using matrix form as follows:

Table 1. Matrix Representation of Transportation Problem

Mathematically (For General case):

x_ij = number of units shipped from supply point i to demand point j.

Then the general formulation of a transportation problem is:

Minimize

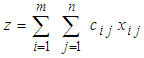subject to ;

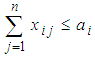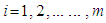(Supply constraints)

;

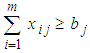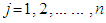(Demand constraints)

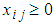. for all 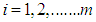and .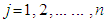

In the case of Balanced TP may be written as

Minimize .

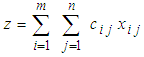subject to 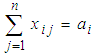; 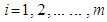(Supply constraints)

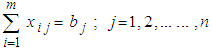(Demand constraints)

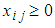; for all 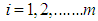and .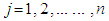

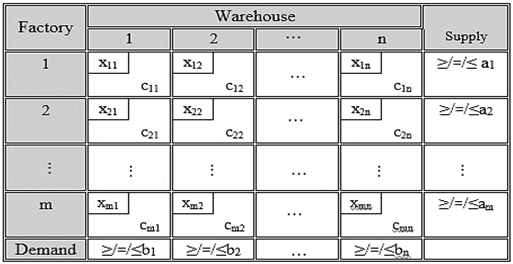
3. Formulation of Transportation Problem with Mixed Constraints

Transportation problem with mixed constraints can be described as follows:

Suppose there are m origins O_i (iS={1,2,3,………m}) and we partitioned them into three sets S₁, S_2, S₃. The set S₁ must distribute exactly a_i units of supply, S₂ must distribute at least a_i units of supply and S₃ must distribute at most a_i units of supply. Also, there are n destinations D_j (jT={1,2,3,………n}) and we partitioned them into three sets T₁, T_2, T₃. The set T₁ must receive exactly b_i units, the set T₂ must receive at least b_i units and the set T₃ must receive at most b_i units of demand. The objective is to determine the amount x_ij transported from source 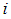to destination 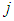while minimizing the total transport cost when satisfying mixed type supply and demand constraints.

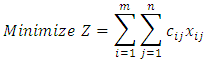Subject to

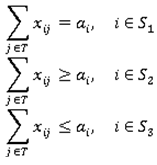and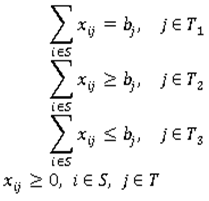

We can also represent the above Transportation Problem with Mixed Constraints (TP-MC) by matrix form as follows:

Table 2. Matrix Representation of Transportation Problem with mixed constraints

4. Proposed Algorithm

The proposed algorithm for determining the initial solution consists of the following steps:

Step 1: Construct the transportation table with mixed constraints for the given problem.

Step 2:

We convert the TP with mixed constraints into Equivalence Standard Balance Transportation Problem (ESBTP) by introducing dummy row and column with cost 1 against the equal (=) and at least (≥) type constraints and cost 0 against the at most (≤) type constraints.

Also setting

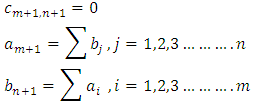Finally, we get balance TP with equality constraints.

Step 3:

Solve the ESBTP can be solved by using Vogel’s approximation method (VAM).

Step 4:

Shift the allocation from dummy cell to original cell by using the transformation:

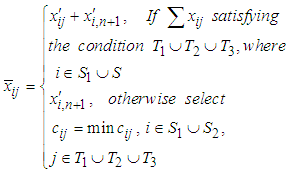And Continue this process until all allocations are satisfied for all row and similarly for a column that is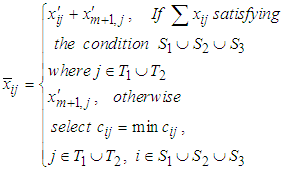

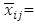optimal solution of the original problem,

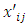= optimal solution of ESBTP.

Step 5:

Finally, compute the total transportation cost for the feasible allocations as the sum of the product of cost and corresponding allocated value of the transportation matrix and total unit of flow.

Remarks:

We consider Problem TP is bounded. Necessary and sufficient conditions for the existence of a feasible solution are found in Brigden (1974). Problem TP will be unbounded if there exists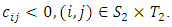

5. Numerical Illustration

Example 1

There are three factories and four warehouses and the factory produces a homogeneous product. Factory A has a production capacity of exactly 20 units, Factory B has a production capacity of at least 16 units and Factory C has a production capacity at most 25 units. Likewise, Warehouse 1 having a capacity of demands at least 11 units, Warehouse 2 having a capacity of demands at most 13 units, warehouse 3 having a capacity of demands at least 17 units. Warehouse 4 having a capacity of demands exact 14 units. If per unit shipping cost from each factory to each warehouse is 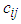which are given. Then this type of TP is called Transportation problem with mixed constraints and we conclude the minimum transportation cost with shipping units (flow) using our proposed method:

Step-1: Formulation –

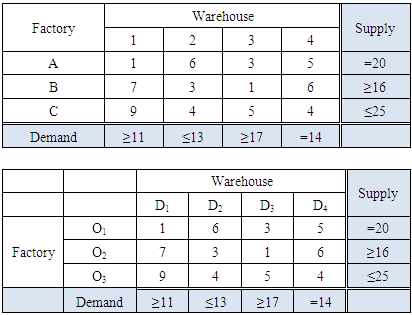Step-2: Convert TP-MC to Equivalence Standard Balance Transportation (ESBTP) Problem:

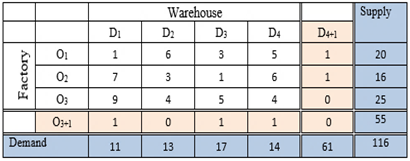Step-3 This is a balanced transportation problem. We solve it by using Vogel’s approximation method (VAM) and we get the allocation below:

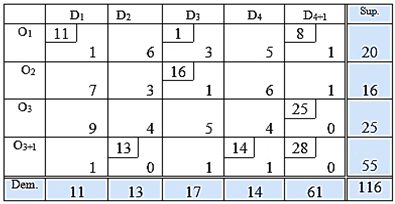Step-4: Now using transformation we get our required solution. Which is:

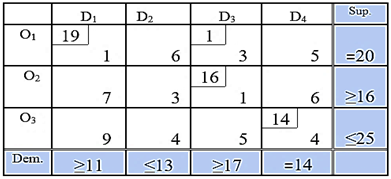Step-5: So required allocations are:

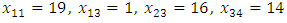, Total unit of flow-50

Total Cost = .

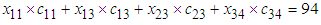The rest of the three examples are given below for making a comparison.

Example 2: [Ref: Klingman, D. et al., (1974)]

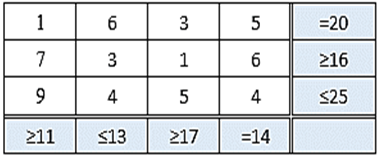Example 3: Ref: Mondal, R.N. et al., (2015)

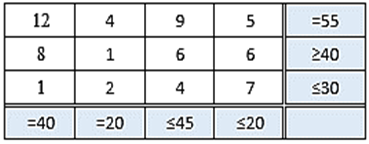Example 4: Ref: Panadian, P. et al., (2010)]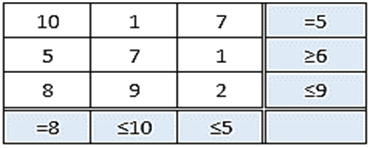

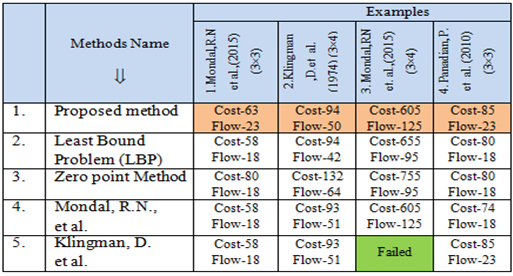
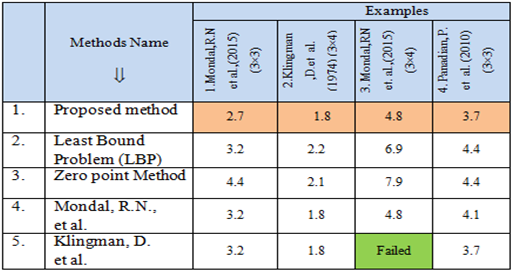
6. Comparative Study

The accompanying Table-3 demonstrates an examination for expense alongside the total unit of flow. Arrangements got by our proposed calculation and the other well-known existing calculations and Table-4 speak to the per-unit cost from where we effortlessly distinguish the best calculation.

Table 3. A Comparative Study of Different Solutions Shows cost and flow of the unit

Table 4. Comparative study shows per unit cost

7. Conclusions

In this paper, we have developed an effective algorithm for solving transportation problems with mixed constraints. A comparative study is carried out here on twenty randomly selected problems of a different order from some reputed journals. This comparison shows that our proposed method gives a better outcome over other existing calculations and we trust this new idea will help individuals who are working in this field. Still, there exists a rich opportunity for further research in this subject.

Declarations

Funding: No funding was received.

Conflicts of interest: On behalf of all authors, the corresponding author states that there is no conflict of interest.

Availability of data and material: Not Applicable.

Code availability: Not Applicable.

Acknowledgement: Not necessary.