American Journal of Operational Research

p-ISSN: 2324-6537    e-ISSN: 2324-6545

2020;  10(3): 45-48

doi:10.5923/j.ajor.20201003.01

Received: Sep. 23, 2020; Accepted: Oct. 6, 2020; Published: Oct. 15, 2020

 

Improved Multi Goal Programming Technique

Chandra Sen

Professor (Rtd.), Department of Agricultural Economics, Institute of Agricultural Sciences, Banaras Hindu University, Varanasi, India

Correspondence to: Chandra Sen , Professor (Rtd.), Department of Agricultural Economics, Institute of Agricultural Sciences, Banaras Hindu University, Varanasi, India.

Email:

Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.

This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract

Multi Goal Programming (MGP) is an extension of Goal Programming used for achieving multiple conflicting goals simultaneously. Several MGP techniques have been developed and used for solving multi goal optimization problems during last three decades. These MGP techniques are based on minimization of sum of deviations between goals and their achievements. For the incommensurate goals, the summing these deviations seems illogical. This problem has been resolved in the proposed an improved MGP technique for solving MGP problems. The results of solving two examples by these technique have shown the superiority of the Improved MGP technique.

Keywords: Goal Programming, Single Goal Programming, Multi Goal Programming

Cite this paper: Chandra Sen , Improved Multi Goal Programming Technique, American Journal of Operational Research, Vol. 10 No. 3, 2020, pp. 45-48. doi: 10.5923/j.ajor.20201003.01.

Article Outline

1. Introduction
2. Methodologies to Solve MGP Problems
    2.1. Existing MGP Model
    2.2. Misconceptions in the Existing MGP Model
3. Improved MGP Model
4. Examples
5. Solution
6. Conclusions
Compliance with Ethical Standards

1. Introduction

Multi Goal Programming is a technique often used to find a compromised solution in achieving multiple conflicting goals. MGP was introduced by Charnes and Cooper [1] and further extended by Ignizio [2], Tamiz, Jones, and Romero [5], and Romero [6]. Weighted Sum Goal Programming (WSMGP) and Preemptive Goal Programming (PGP) techniques have been popularly used by Ajayi-Daniels [14], Kanan, Acharya and Acharya [10] and Qahtani, El–Hefnawy, El–Ashram, and Fayomi [13] for solving multi goal programming problems. Dave, Abha [8] and Cinthia [9] suggested the application of multi goal programming for managing agriculture efficiently. A sustainable development plan for India was prepared using MGP by Gupta, Fügenschuh and Ali [11]. Mohammadiana, Babaeia, Jarrahi, and Anjomrouzb [12] used MGP for scheduling the nurse shifts in a hospital for improving the efficiency of the nursing services to the patients. Goal programming technique was applied to determine the optimal number of students to be enrolled in different disciplines by Rashid, Halim and Hassan [15]. Ojo, Farayibi and Akinnuli [16] used multi goal programming for procurement of various equipments in a manufacturing industry. Priyadharshini and Anju [17] applied the goal programming for solving the transport problem. A Several variants of multi goal programming have also been proposed in the past three decades. However, proper attention has not been given to the conceptual framework of the techniques. Few methodological issues of MGP and weight sum multi goal programming (WSMGP} have been discussed in the limited studies by Min, and Storbeck [3], Rifai [4], Orumie, and Ebong [7]. The present study points out a few weaknesses in the basic structure of MGP/WSMGP techniques and proposes an improved technique for generating appropriate solutions.

2. Methodologies to Solve MGP Problems

2.1. Existing MGP Model

The existing multi goal programming model can be expressed as:
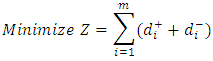Subject to:
Goal Constraints
System constraints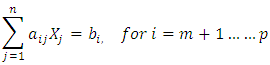
There are 'm' Goals, 'p' System constraints and 'n' decision variables
Z= Objective function/ Summation of all deviations
aij= the coefficient associated with jth variable in ith Goal/constraint
Xj= the jth decision variable
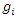= the right hand side value of ith goal
bi= the right hand side value of ith constraint
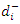= negative deviational variation from ith goal (under achievement)
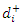= positive deviational variation from ith goal (over achievement)

2.2. Misconceptions in the Existing MGP Model

a. The MGP models help the decision-maker to obtain an appropriate solution for achieving multiple goals. Often multiple goals are conflicting and are achievable only at the expense of other goal/s. The goals may be incommensurable. The summation and subtraction of deviations of multi dimensional values seems not logical.
b. In the presence of high deviations in the coefficients of decision variables of different goals, the MGP solution may be biased towards the goal/s with higher values of coefficients.

3. Improved MGP Model

The abovementioned problems can be resolved by scalarizing the objective function as described below. This makes the deviations free of dimensions.
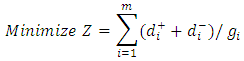Subject to:
Goal Constraints
System constraints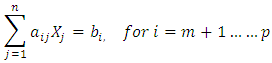
The above techniques have been used to solve the following examples.

4. Examples

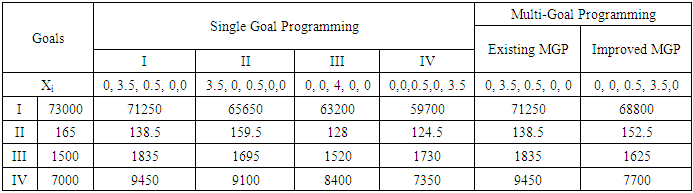
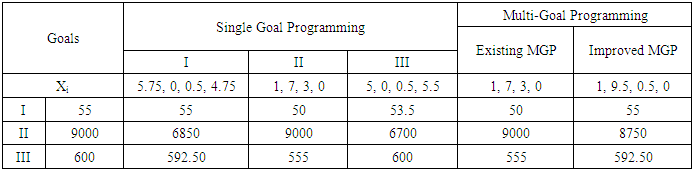
Two examples have been solved using existing and Improved MGP.
Example 1
Goal-I: 16500X1 + 18100X2 + 15800X3 +17400X4 + 14800X5 = 73000
Goal-II: 41X1 + 35X2 + 32X3 +39X4 + 31X5 = 165
Goal-III: 430X1 + 470X2 + 380X3 +410X4 +440X5 = 1500
Goal-IV: 2300X1 + 2400X2 + 2100X3 +1900X4 +1800X5 =7000
Subject to:
X1 + X2 + X3 +X4 + X5 = 4
2X3 ≥ 1
X1, X2, X3, X4, X5 ≥ 0
Example 2
Goal-I: 6X1 + 5X2 + 3X3 + 4X4 = 55
Goal-II: 700X1 + 800X2 + 900X3 + 500X4 = 9000
Goal-III: 50X1 + 55X2 + 40X3 + 60X4 = 600
Subject to:
X1 + X2 + X3 +X4 = 11
X1 ≥ 1
2X3 ≥ 1
X1, X2, X3, X4 ≥ 0

5. Solution

Example 1 has been solved using single as well as MGP techniques. The results are presented in Table 1. All four solutions of single goal optimization are quite different. Each solution achieves one goal only and ignores the remaining three goals. The first solution achieves the first goal up to 71250 which seems superior to the remaining three goal achievements. The value of the second goal achieved was 159.50 which was close to its goal of 165. Similar results have been obtained in the achievements of third and fourth goals. The results of existing and improved MGP techniques are presented in the last two columns of Table 1.
Table 1. Goal Achievements in Single and Multi-Goal Programming
     
The solution of the existing MGP technique is the same as the first solution of the single goal programming technique. This is due to larger values of the coefficients of decision variables of the first objective function. Similar problems may be noticed with the goals of different dimensions. However the improved MGP technique generated the solution that achieves all the goals simultaneously. The value of the first goal achievement is 68800 which is less than the single goal achievement of 71250 but superior over the remaining three single goal optimizations. The achievements of the remaining three goals were also compromising and acceptable. This reveals the superiority of improved MGP over the existing MGP technique.
The solution of example 2 has been presented in table 2. The results of single goal optimization are similar to the first example. The single goal optimization of first goal has achieved it fully with its value 55 but ignored the second and third goal. The achievements of second and third goals have also generated similar results. The solution of existing MGP is same as the achievement of the second goal which is not achieving the remaining goals first and third. However, the improved MGP has achieved all the three goals simultaneously. It has achieved first objective fully with the achievements of second and third goals as 8750 and 592.50 respectively which are closer to their respective goals.
Table 2. Goal Achievements in Single and Multi-Goal Programming
     

6. Conclusions

The present study tried to identify a few methodological issues in the existing MGP technique and proposed an improved MGP technique. Existing and improved MGP techniques have been tested with two suitable examples. The existing MGP technique failed to achieve all the goals simultaneously. However, the improved MGP technique have provided superior solution in achieving the desired goals simultaneusly.

Compliance with Ethical Standards

Conflict of interest: The author declares that there is no conflict of interest.

References

[1]  Charnes, A., & Cooper, W. W. (1961). Management model and industrial application of linear programming. New York: Wiley.
[2]  Ignizio, J. P. (1985). Introduction to linear goal programming, Beverly: Hills, CA: Sage.
[3]  Min, H. and Storbeck, J. (1991). On the Origin and Persistence of Misconceptions in Goal Programming. Journal of the Operational Research Society, 42, (4), 301-312.
[4]  Rifai, A. K. (1996). A note on the structure of the goal-programming model: assessment and evaluation. International Journal of Operations & Production Management, 16 (1), 40-49.
[5]  Tamiz, M., Jones, D., & Romero, C. (1998). Goal programming for decision making: an overview of the current state-of-the-art. European Journal of Operational Research, 111, 567-581.
[6]  Romero, C. (2001). Extended lexicographic goal programming: a unifying approach. Omega, 29, 63- 71.
[7]  Orumie, U.C., and Ebong, D. (2014) A Glorious Literature on Linear Goal Programming Algorithms. American Journal of Operations Research, 4, 59-71.
[8]  Dave, Abha (2015). Goal Programming Applications in Agricultural Management. International Research Journal of Engineering and Technology (IRJET), Vol. 2 (6), 883-887.
[9]  Cynthia, O. U. (2017). New Approach to Solving Generalized Linear Goal Programming Problem. Mathematics Applied in Science and Technology. Vol. 9, (1) 1-22.
[10]  Kanan K. Patro, M. M. Acharya & S. Acharya (2018) Multi-choice goal programming approach to solve multi-objective probabilistic programming problem, Journal of Information and Optimization Sciences, 39:3, 607-629.
[11]  Gupta, S., Fügenschuh, A. and Ali, I. (2018). A Multi-Criteria Goal Programming Model to Analyze the Sustainable Goals of India. Sustainability, Vol.10 (778), 1-19.
[12]  Mohammadiana, M., Babaeia, M. A. Jarrahi, M. A., Anjomrouzb, E. (2019) Scheduling Nurse Shifts Using Goal Programming Based on Nurse Preferences: A Case Study in an Emergency Department. IJE TRANSACTIONS A: Basics Vol. 32, No. 7, 954-963.
[13]  Qahtani, H. Al., El–Hefnawy, A., El–Ashram, M. M., and Fayomi, A. (2019). A Goal Programming Approach to Multichoice Multiobjective Stochastic Transportation Problems with Extreme Value Distribution. Advances in Operations Research. Vol. 2019, 1-6.
[14]  Ajayi-Daniels, E. E. (2019). Resource Optimization in a Fashion Firm: A Goal Programming Approach. International Journal of Management and Fuzzy Systems, 5 (1), 14-20.
[15]  Rashid N. R. M., Halim B. A. and Hassan N.. (2020) Optimization of the Allocation of Students into Academic Programmes using Goal Programming. ASM Science Journal, Vol. 13, 1-8.
[16]  Ojo O. O., Farayibi P. K. and Akinnuli B.O. (2020) Modified Goal Programming Model for Limited Available Budget Allocation for Equipment Procurement under Inflation Condition. Advances in Research. Vol. 21(4): 25-35.
[17]  Priyadharshini, P. and Anju, A. (2020). Type-2 Duality Triangular Fuzzy Fractional Transportation Problem using Goal Programming Technique. International Journal of Recent Technology and Engineering (IJRTE), Vol. 8(6) 1295-1303.