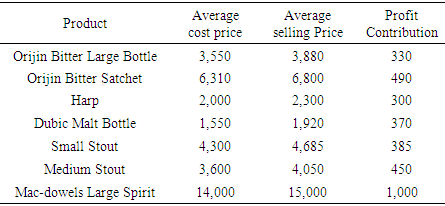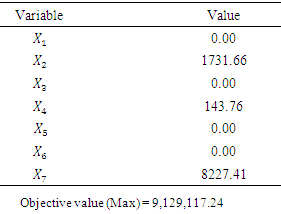-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2020; 10(2): 39-43
doi:10.5923/j.ajor.20201002.03
Received: Aug. 24, 2020; Accepted: Sep. 9, 2020; Published: Sep. 26, 2020

Application of Linear Programming on the Profit Maximization of Nigerian Bottling Company
P. N. Ezra1, A. V. Oladugba1, F. O. Ohanuba1, N. O. Igwe2, C. A. Okonta2
1Department of Statistics, University of Nigeria, Nsukka
2Department of Maths / Statistics, Akanu Ibiam Federal Polytechnic, Unwana
Correspondence to: P. N. Ezra, Department of Statistics, University of Nigeria, Nsukka.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

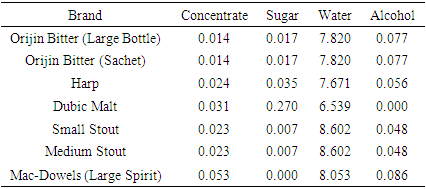
Nigerian Bottling Company is into production and selling of such products as Orijin Bitter Large bottle, Orijin Bitter Sachet, Harp, Dubic Malt, Small Stout, Medium Stout, and Mac-dowels Large Spirit. Production has to do with transforming raw materials into products in order to maximize a Company’s revenue. It has been the quest of Nigerian Bottling Company to have a structured process with documented steps and measurable results so as to establish a trend for the profit making of the business. In view of this, in this study, linear programming model was used to allocate raw materials (resources) to the production of the above mentioned Company’s products so as to know the right product mix that actually maximizes the Company’s profit and in what capacities. Data collected on these known products were analysed using simplex algorithm of linear programming with the help of Tora Software and the result showed that 1,732 crates of Dubic Malt with the objective coefficient (490), 144 cartons of Orijin bitter sachets with the objective coefficient (370) and 8,227 crates of Mac-dowel Spirit with the objective coefficient (1000) sold in a day yielded a profit of ₦9,129,117.24. Also, sensitivity analysis was carried out to know the maximum and minimum unit profits (i.e, the objective function cost coefficients) of the concerned products and the resource quantities within which the maximum profit of the Company should be maintained. The result of the sensitivity analysis also revealed the shadow price (dual price) which is the cost of acquiring an additional resource in case the Company has any of such needs. Based on the results obtained from this research, it is recommended that Nigerian Bottling Company should invest more in the production of those products that maximize their profit.
Keywords: Linear Programming, Optimization, Objective function, Inequality Constraints and Optimal Solution
Cite this paper: P. N. Ezra, A. V. Oladugba, F. O. Ohanuba, N. O. Igwe, C. A. Okonta, Application of Linear Programming on the Profit Maximization of Nigerian Bottling Company, American Journal of Operational Research, Vol. 10 No. 2, 2020, pp. 39-43. doi: 10.5923/j.ajor.20201002.03.
Article Outline
1. Introduction
- Every business organization seeks the best way to go about their business in order to maximize profit with their available limited resources. Optimal production planning and care are therefore required in order to sustain the optimal profit making and existence of such organization: See [9] and [11]. Production planning in this regard has to do with putting in place various activities and measures in order to ensure optimal production that satisfies customers’ demands, considering the fact that the real world resources such as material, money, manpower, space and time are limited: See [7], [8] [12] and [14]. Every company has a number of product lines which consist of the product mix that such a company deals on. Product-mix determination is very important as it helps a given company to focus its production on relevant products that enhance profit making. Nevertheless, a company may be tempted to add more product lines in their quest to have more customers; thereby entering into the risk of including such products that appeal only to a fraction of its customer base. Considering the fact that different products require different amounts of production resources having different costs and revenues at different stages of production, there is need for a mathematical technique that can determine the product mix that will maximize the total profit: See [5] and [14]. This mathematical technique is called “Linear Programming (LP) model.”Linear Programming also called linear optimization is a technique for the optimization of a linear objective function, subject to linear inequality and sometimes equality constraints: See [2], [3] and [4]. It is an operational research technique used to allocate limited production resources for a firm’s best practices: See [1], [3] and [12]. This calls for model formulation which is very important as it represents a real life situation or system for competent decision analysis: See [2], [3] and [7]. Most times, production mix problems reach complexity when for instance about five (5) or more products of the same department are involved and this makes algebraic solution difficult and cumbersome. A procedure for solving any large problem of such nature is the simplex method (tableau) which uses iterative procedures in solving linear programming problems: See [4]. The manual solution of a linear programming model using the simplex method can be lengthy and tedious but can be quicker and accurate when computer (TORA software or any other software that can handle LP) is used. [11] used LP model to schedule drivers in a transport co-operation so as to determine the minimum number of drivers needed for each shift in a day in order to reduce the amount spent for the reserved drivers. [15] considered linear programming model as a quantitative decision making tool needed for proper optimization of product mix in an apparel industry. [8] used big M and dual simplex methods as alternative methods of finding solutions to linear programming that can reduce the number of iteration and also save valuable time. [1] used the simplex algorithm of linear programming for the optimal allocation of raw materials for the production of different sizes of bread in a bakery industry. [14] discovered that intercept values could be used to find out the equality constraints among the inequality constraints in order to achieve optimal solutions while solving linear programming problems. [10] used simplex method of linear programming to determine which bread size contributed the highest to the profit maximization of the company. Sensitivity analysis was also carried out to determine the minimum and maximum cost coefficients of the bread sizes within which the company’s optimal profit could be maintained.The purpose of this research is to determine how the limited resources (raw materials) of Nigeria Bottling Company could be allocated in order to maximize profit. It is aimed at determining the product(s) that contribute(s) maximally to such profit. The data on which this is based are quantities of raw materials available in stock, cost and selling prices and also the profits from crates of each product. The profit constitutes the objective function while raw materials available in stock are used as constraints. In every optimization problem, due to the limited nature of resources, it is always of interest not only to obtain an optimal solution of the problem but also to find how stable that optimal solution would be, assuming there changes either the objective function’s cost coefficient or the right hand side resource constraint. In view of this, we carried out sensitivity analysis so as to determine the quantities of the variables (the company’s products) that would give the optimal solution, the range of values of such variables within which the optimal solution should not deteriorate and also the shadow price (also known as the dual price) which is the price for acquiring an additional unit of each resource (in case the company runs short of any) for optimal production.
2. Material and Methodology
2.1. Material
|
|
|
2.2. Methodology
2.2.1. Linear Programming Model
- In order to grant the quest of the Nigerian Bottling Company on establishing a structured process with documented steps and measurable results in allocating their raw materials for optimal production that will enhance the profit making of the business, the maximization linear programming model given below has been considered the most efficient.
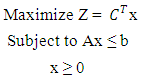 | (1) |
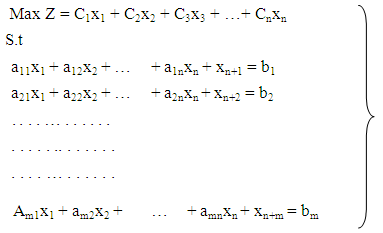 | (2) |

3. Data Analysis
- In order to achieve the purpose of this study which is to obtain the best product mix that will lead to maximization of the Company’s profit, simplex method procedures outlined in Section 2 were applied to the data presented in Tables 1, 2, and 3. The models consist of the objective function and the constraints as shown by (2). For the profit maximization of the concerned company, the LP model was formulated using the data values in Tables 1, 2, and 3 as follows:
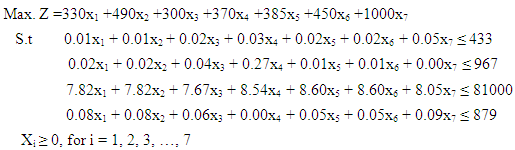 The problem in standard form is as shown below:
The problem in standard form is as shown below: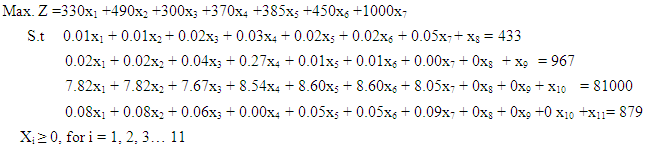 Where x8, x9, x10 and x11 are the added slack variables.
Where x8, x9, x10 and x11 are the added slack variables.
|
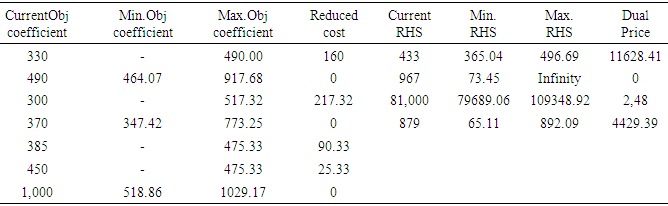
3.1. Sensitivity Analysis
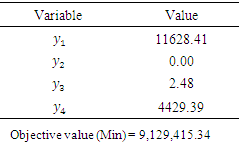
- In this section, sensitivity analysis was carried out to know the extent to which any of the input data (that is, the per unit profit of any of the products (variables) or the available resources) of the company can change without affecting the optimal solution. The result of the sensitivity analysis also showed the dual prices also known as the shadow prices to enable the company know the cost of acquiring an additional unit of any of their resources in case there is need for that. In carrying out sensitivity analysis using the dual variables, the dual problem was formulated from the original (primal) problem above as follows:
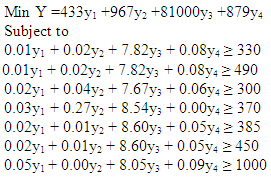 where yis ≥ 0, for i=1,2,…,4 are the dual variables.The problem in standard form is as shown below:
where yis ≥ 0, for i=1,2,…,4 are the dual variables.The problem in standard form is as shown below: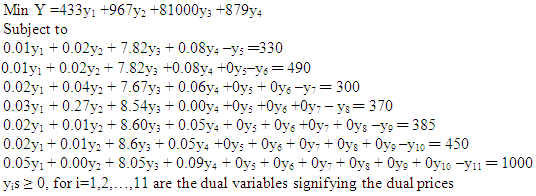 where y5, y6, y7…y11 are the added surplus variables. The analyses (accomplished in 10 iterations) were done using Tora Software.
where y5, y6, y7…y11 are the added surplus variables. The analyses (accomplished in 10 iterations) were done using Tora Software.
|
|
4. Result Discussion and Conclusions
- In this research, the major aims were to decide how the limited resources of Nigeria Bottling Company would be allocated in order to maximize profit and also determine the right product mix that would maximize such profit. From the result of the analysis, it was discovered that Dubic Malt, Orijin bitter sachet and Mac-dowel Spirit contributed maximally to the profit of the company. Their production quantities on daily basis should be 1,732, 144 and 8,227 crates respectively yielding the total profit of ₦9,129,117.24. Also, the dual problem formulated from the original (primal) problem was used to conduct sensitivity analysis in order to determine the feasibility of the already obtained optimal solution above. The result of the sensitivity analysis presented in Table 6, showed the various reduced costs (that is, the ranges of increments) of the objective cost coefficients of the involved variables and the shadow prices of the RHS resource constraints within which the solution remains optimal. The result of the sensitivity analysis also revealed the shadow price (dual price) which is the cost of acquiring an additional resource in case the Company has any of such needs. Finally, based on the results obtained from this research, it is recommended that Nigerian Bottling Company should focus more on producing those products that maximize their profit.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML