P. N. Ezra1, A. V. Oladugba1, F. O. Ohanuba1, P. N. Opara2
1Department of Statistics, University of Nigeria, Nsukka
2Department of Statistics, Imo State Polytechnic, Umuagwo
Correspondence to: P. N. Ezra, Department of Statistics, University of Nigeria, Nsukka.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Goal optimization is an optimization technique which considers more than one objective and each of the objective functions is given a goal or target to be achieved. In goal optimization, the given objective functions are not maximized or minimized directly; rather, the unwanted deviations between the set goals and the actual values obtained are minimized. The aim of this study is to develop a goal programming model that could be used to optimize the daily production of Pastry Company. The three goals considered here are: maximizing the daily sales’ profits, minimizing the cost of production and maximizing the utilization of machines used in producing the company’s products. Data were collected on pastry products such as bread, cake, chinchin, meat pie and fish pie from the day to day production and sales records of the company. The two methods of solution for goal programming models, namely, the weights and preemptive methods were applied. Tora software was used for the analyses and based on results of the analyses, it was concluded that neither of the two methods of solution is superior to the other and that each technique is designed to satisfy certain decision maker’s preferences.
Keywords:
Goal programming, Production, Optimization, Deviational variables, Small and medium enterprise
Cite this paper: P. N. Ezra, A. V. Oladugba, F. O. Ohanuba, P. N. Opara, Goal Optimization of a Pastry Company, American Journal of Operational Research, Vol. 10 No. 1, 2020, pp. 17-21. doi: 10.5923/j.ajor.20201001.03.
1. Introduction
Often times, individuals, companies, organizations and even institutions seek to find the best way to go about their businesses or jobs in order to maximize profit and also satisfy some other necessary objectives that may be of importance to them. Multiple objectives arise in production companies as a result of the existence of several departments where each department has peculiar objective(s) to achieve. This calls for decision making in which the decision maker accepts a particular solution based on some laid down criteria. Optimal production planning and care are therefore required since the decision makers in such companies might not be willing to allow any arm of the business (es) to suffer as much as it is in their power to make all things well: See [6], [9], [12] and [14]. Production planning in this regard has to do with putting in place various activities and measures in order to ensure optimal production that satisfies customers’ demands, considering the fact that the real world resources such as budgets, labour and time are limited: See [6], [12] and [14]. In any production planning, profit making is always of uppermost importance, followed by cost minimization and then the effective use of the available machines: See [5] and [11]. The design of an efficient production planning system can only be possible when there is a strong grasp of the production environment in terms of customers, products and production processes: See [7] and [11]. Such scenarios as described above are better handled by mathematical programming models of which Linear Programming (LP) model is the basic from which every other programming model originates. According to [1], [5] and [14], Goal Programming (GP) is an extension of Linear Programming, which is commonly used to deal with multi-objective problems by minimizing deviations of goals defined by decision maker(s), with efforts aimed at achieving objectives that match the existing limited resources. [2] as well as [3] added that the basic idea of goal programming is to assign a specific numeric goal to each of the objectives and then seek a solution that minimizes the deviations of these objectives from their respective goals. [2], [4] and [6] noted that in order to minimize the deviation in a particular goal, a variable called a "deviation variable (di = di- or di+)” is assigned to each goal. It was stated that such variable represents the amount by which the goal is not achieved. It was further explained that if the concerned deviation variable is minimized to zero, it implies the exact attainment of the corresponding goal. It was also emphasized that if complete attainment of any goal is not possible, goal programming provides the decision maker with the information on the amount by which the goal is not achieved. According to [3] and [4], the two algorithms for solving goal programming problems are: the weights method and the preemptive method. There, it was declared that both methods convert the multiple objectives into a single objective function called the achievement function. It was also noted there that in the weights method, the objective function also known as the achievement function comprises the weighted sum of the deviations of the goals from their aspiration levels and these weights being subjective are assigned by the decision maker according to the relative importance of each goal while the preemptive method on the other hand starts by prioritizing the goals in their order of importance such that higher goals are achieved before the lower ones: See [4]. Also, it was asserted that the two methods do not generally produce the same solution and that neither of the methods is superior to the other as each technique is designed to satisfy certain decision maker’s preferences. [5] applied the weighted goal programming mathematical model to a building construction project in order to estimate the categories and the number of residential apartments. [4] used a preemptive goal programming model for production planning where three objectives were optimized hierarchically. [7] used the three different optimization techniques, namely: Linear Programming (LP), Priority Weighted Goal Programming (PWGP) and Chebyshev Goal Programming (CGP) (which is a special form of weighted goal programming) to optimize goal constraints of a small scale enterprise and discovered that the Priority Weighted Goal Programming model performed better than LP and CGP models. [10] discovered that most methodologies used in linear programming problems like simplex method, duality and sensitivity analysis could equivalently apply to goal programming problems. The objective of this study is to develop a goal programming model for a real life production situation in a pastry company producing pastry products such as bread, cake, chinchin, meat pie and fish pie where the interest is to minimize underachievement of the profit target (d1-), overachievement of cost of production (d2+) and underutilization of the machine capacity (d3-).In every optimization problem, due to the limited nature of resources, it is always of interest not only to obtain an optimal solution of the problem but also to find how stable that optimal solution would be, assuming there changes either the objective function’s cost coefficient or the right hand side resource constraint: See [8]. In view of this, in this our work, we carried out sensitivity analysis so as to determine the quantities of the cost coefficients and resources that would give the optimal solution, their minimum and maximum limits within which the optimal solution could not deteriorate and the degree of attainment of the set goals. Also, the results of the sensitivity analysis showed the shadow prices, also known as the dual prices, which are the prices for acquiring additional units of resources in case the company runs short of resources for production.
2. Material and Methodology
2.1. Material
The data used in this study presented in Tables 1, 2, and 3 were collected from Chy Best Pastry Company’s day to day production record on each of the products (bread, cake, chinchin, meat pie and fish pie). The company has 11 workers who are working in different sections, namely; milling, mixing and baking sections. The company’s optimization goals are to maximize the daily profit, minimize the cost of production and maximize the utilization of machines used in the production of the products. The company’s set profit target is ₦350,000 daily to be achieved at the minimum cost of ₦250,000, within 10 hours of machine usage.The various data were categorized into 1) The raw materials available.2) The available machines for the production.3) Time taken to produce each product.4) The average cost of producing and selling price of each product.Table 1. Quantity of raw materials available and the amount needed to produce each product (in kg)
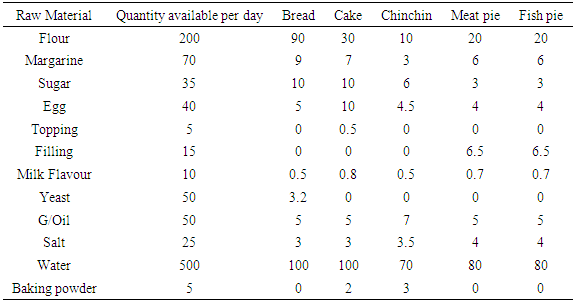 |
| |
|
Table 2. Machine time taken to produce each product (in hours)
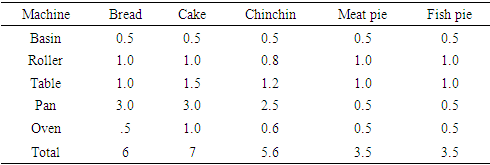 |
| |
|
Table 3. Products and their profit contributions in naira
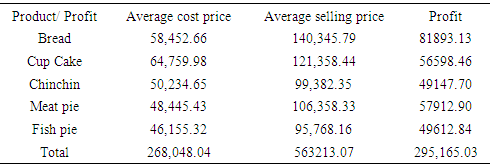 |
| |
|
2.2. Methodology
In this work, both weights method and preemptive method were used and the results were compared.
2.2.1. Goal Programming Model (for Weights Method)
The general form of a GP problem using weights method is expressed as: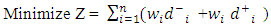 | (1) |
where, i represents the number of goals.subject to 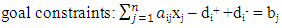 | (2) |
where, j is the number of goal constraints which also depends on the number of goalsand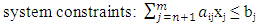 | (3) |
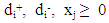 | (4) |
for i = 1,2,…,n and j = 1,2,…, mwhere, wi is the weight for each deviation variable; di+ is the amount by which goal i is overachieved; di- is the amount by which goal i is underachieved; aij is the amount of the ith resource needed by the jth activity; bj’s are the targets or goals associated with the constraints; Xj; j = 1, 2, 3, 4, and 5, is the number of the bread, cake, chinchin, meat pie and fish pie produced per day.Both overachievement and underachievement of a goal cannot occur simultaneously. Hence, either one or both of these variables must have a zero value such that di+di- = 0.
2.2.2. Goal Programming Model (for Preemptive Method)
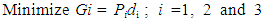 | (5) |
Subject to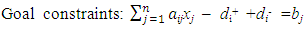 | (6) |
j = i, the number of goal constraints andSystem constraints: 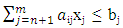 | (7) |
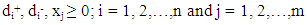 | (8) |
where Pi’s are the different priority levels of the goals from the highest to the lowest. In this work, the first priority goal is to minimize the under achievement of the profit target; the second priority is to minimize the over achievement of the cost of production while the third priority is to minimize the under achievement of machine capacity utilization.
3. Data Analysis
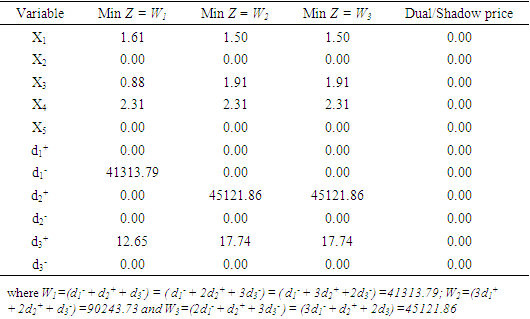
In order to achieve the purpose of this study, simplex method procedures outlined in Section 2 were applied to the data presented in Tables 1, 2, and 3. The analyses were done using Tora Software. The models consist of the objective functions which comprise the concerned deviation variables to be minimized as shown in (1) and (5); and the constraints which comprise the goal constraints and the system constraints as shown by (2) and (3) or (6) and (7); where each model is formulated using the decision and deviational variables. Concerning this study, the required models for different weights assignment are formulated as follows: Minimize Z = d1- + d2+ + d3-; d1- + 2d2+ +3d3-; 2d1- + d2+ + 3d3-; 3d1- + 2d2+ + d3-; d1- + 3d2+ + 2d3-, each Subject toGoal constraints81893.13x1+56598.46x2+49147.70x3+57912.90x4 +49612.84x5 – d1++ d1- = 35000058452.66x1+64759.98 x2+50234.65x3+48445.43x4+46155.32x5–d2++d2- = 2500006x1 + 7x2 + 5.6x3 + 3.5x4 + 3.5x5 – d3++ d3- = 10System constraints90x1 +30x2 +10x3 +20x4 +20x5 ≤ 2009x1 +7x2 +3x3 +6x4 +6x5 ≤7010x1 +10x2 +6x3 +3x4 +3x5 ≤355x1 +10x2 +4.5x3 +4x4 +4x5 ≤400.5x2 ≤ 56.5x4 +6.5x5 ≤150.5x1 +0.8x2 +0.5x3 +0.7x4 +0.7x5 ≤103.2x1 ≤50 5x1 +5x2 +7x3 +5x4 +5x5 ≤503x1 +3x2 +3.5x3 +4x4 +4x5 ≤25100x1 +100x2 +70x3 +80x4 +80x5 ≤500 2x2 +3x3 ≤5x1, x2, x3, x4, x5, d1+, d1-, d2+, d2-, d3+, d3- ≥0; The required models for the preemptive method considering the different goal priorities are formulated as follows: Min G1 = d1-Min G2 = d2+Min G3 = d3-, each Subject toTable 4. Results of the Analyses for the different assigned weights
 |
| |
|
Goal constraints81893.13x1+56598.46x2+49147.70x3+57912.90x4 +49612.84x5 – d1++ d1- = 35000058452.66x1+64759.98x2+50234.65x3+48445.43x4+46155.32x5– d2++ d2- =2500006x1 + 7x2 + 5.6x3 + 3.5x4 + 3.5x5 – d3++ d3- = 10System constraints90x1 +30x2 +10x3 +20x4 +20x5 ≤ 2009x1 +7x2 +3x3 +6x4 +6x5 ≤7010x1 +10x2 +6x3 +3x4 +3x5 ≤355x1 +10x2 +4.5x3 +4x4 +4x5 ≤400.5x2 ≤56.5x4 +6.5x5 ≤150.5x1 +0.8x2 +0.5x3 +0.7x4 +0.7x5 ≤103.2x1 ≤50 5x1 +5x2 +7x3 +5x4 +5x5 ≤503x1 +3x2 +3.5x3 +4x4 +4x5 ≤25100x1 +100x2 +70x3 +80x4 +80x5 ≤500 2x2 +3x3 ≤5x1, x2, x3, x4, x5, d1+, d1-, d2+, d2-, d3+, d3- ≥0; Table 5. Results of the analysis for pre-emptive method
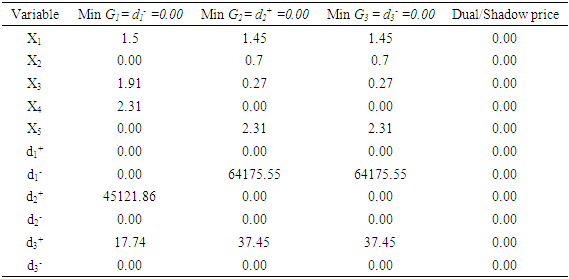 |
| |
|
4. Sensitivity Analysis
In this section, the sensitivity analysis was carried out on the constants of the right hand sides (RSH) of the goal constraint and system constraint equations, and the cost coefficients so as to determine their maximum and minimum limits for optimality. The results are presented in Table 6.Table 6. Result of Sensitivity Analysis for RHS and variable / cost coefficients
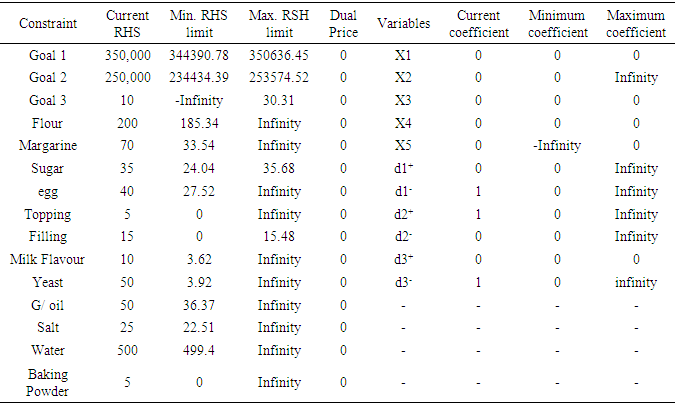 |
| |
|
5. Discussion and Conclusions
In this research, the major aims were to minimize the underachievement of the profit goal (d1-), the overachievement of the production cost goal (d2+), and the underachievement of machine utilization goal (d3-). From the results of the analysis of the weights method shown in Table 4, it was discovered that d1- = 41313.79; d1+ = 45121.86 and d3- = 0; meaning that the profit goal was underachieved by ₦41,313.79; the production cost goal was overachieved by ₦45,121.86 and the machine utilization goal was exactly achieved. Also the results in Table 5 showed that d1- = d2+ = d3- = 0, meaning that all the goals were exactly achieved using the pre-emptive method.The sensitivity analysis presented in Table 6, showed the various minimum and maximum limits of the RHS constraints and cost / variable coefficients within which the solution remains optimal. Furthermore, the fifth column showed that the shadow price (dual prices) for each RHS constraint was zero; meaning that using additional units of the resources would not alter the optimal solution provided the limits were not violated. Finally, based on the results of the analysis, we therefore concluded that neither of the two methods of solution is superior to the other; rather, each technique is actually designed to satisfy certain decision maker’s preferences.
References
| [1] | Bushra, A. H. 2015, “Bank Financial Statement Management using a Goal Programming model”, Procedia – Social and Behavioral Sciences 211, 498 – 504. |
| [2] | Chowdary, B. V. and Slomp, J., 2002, “Production Planning under Dynamic Product Environment: A multi-objective Goal Programming Approach”, Research Report. University of Groningen. |
| [3] | Dinesh, K and Sridhar, K. 2016, “Multiple Objective Operations Decisions by using Goal Programming for a small scale enterprise.” International Journal of Research in Engineering and Technology. Vol. 4, Issue 6, 7-12. |
| [4] | Dhoruri, A., Lestari, D. and Ratnasari, E., 2017, “Sensitivity Analysis of Goal Programming Model for Dietary Menu of Diabetes Mellitus Patients,” International Journal of Modeling and Optimization. Vol.1, No. 7. |
| [5] | Hada, D. S. 2017, “Applying Weighted Goal Programming to project management decisions with multiple goals,” Indian Journal of Scientific Research, 15 (1): 100-108. |
| [6] | Jong, C. H., Medina, N., Fakhriyah, N., Hidayat, C. and Hamali, S., 2018, “Using Goal Programming Method for Optimization of Production Planning,” International Conference on Information Management and Technology, 155-159. |
| [7] | Kumar, P. P. 2019, “Goal Programming through bakery Production,” International Journal of Scientific and Technology Research, Vol. 8, Issue 10, 3722-3725. |
| [8] | Kumar, P. P., Vinodkumar, O. and Yugandhar, T., 2018, “an optimization technique on the managerial decision making,” International Journal of Mechanical and Production Engineering Research and Development, Vol. 8, Issue 6, 507-516. |
| [9] | Leung, S. C. H. and Ng, W., 2007, “A Goal Programming Model for Production Planning of Perishable Products with Postponement,” Journal of Computer and Industrial Engineering, 53(1), 531-541. |
| [10] | Nabendu, S. and Manish, N., 2012, “An Optimal Model using Goal Programming for Rubber Wood Door Manufacturing factory in Tripura,” Department of Mathematics, Assam University, Silchar-788011, India. |
| [11] | Nasruddin, H., Afifah, H. P., Nur, S. I. and Nurul, F. R., 2013, “A Goal Programming Model for Bakery Production,” Advances Environmental Biology, 7(1); 187-190. |
| [12] | Olhager, J. and Wikner, J., 2002, “Production Planning and control tools”, Production Planning and Control, 11(3): 210-222. |
| [13] | Safiai, S., Hassan, N., Mohammad, N. H. and Raduan, Z. A., 2012, “Goal programming formulation in Nutrient Management for Chilli Plantation in Sungai Buloh, Malaysia,” Advances in Environmental Biology, 6(12); 4008-4012. |
| [14] | Sen, N. and Nandi, M., 2012, “A Goal Programming Approach to Rubber Plantation Planning in Tripura”, Applied Mathematical Science, 6(124) 6171-6179. |



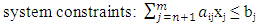
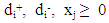
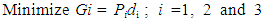
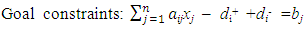
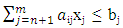
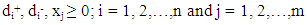
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML




