-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2020; 10(1): 8-16
doi:10.5923/j.ajor.20201001.02

Stochastic Inventory System with Reneging of Customers from the Service Facilities
Mohammad Ekramol Islam 1, Rupen Barua 2, Mohammad Ataullah 3, Ganesh Chandra Ray 4
1Department of Business Administration, Northern University Bangladesh, Dhaka
2Assistant Professor of Mathematics, DSHE, Ministry of Education, Bangladesh, Dhaka
3Assistant Professor of Mathematics, DSHE, MoE, Bangladesh, Dhaka
4Department of Mathematics, Chittagong University, Bangladesh, Chittagong
Correspondence to: Mohammad Ataullah , Assistant Professor of Mathematics, DSHE, MoE, Bangladesh, Dhaka.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

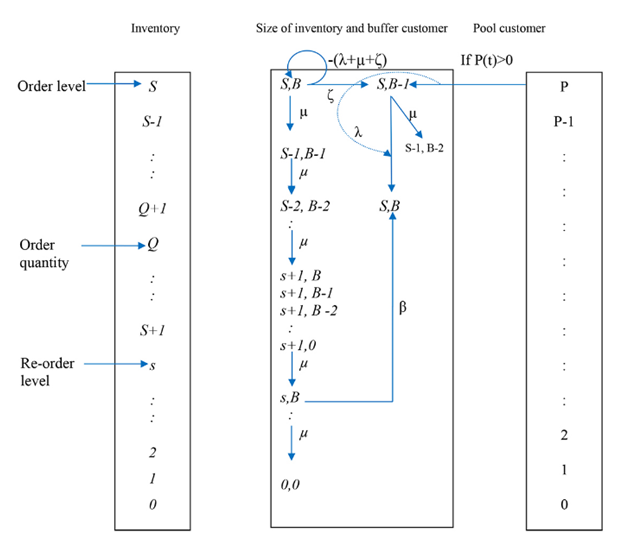
This paper analysis an (s, S) perishable inventory system with postponed demands with service facilities. We assume that customer arrive to the service according to Poisson process with parameter λ. In this system, there is a finite buffer whose capacity varies according to the inventory level at any given time. When the maximum buffer size is reached, further demands join a pool which has finite capacity M (<∞) with probability γ and with probability (1-γ) it is lost forever. When inventory level is larger than the number of customers in the buffer, an external demand can enter the buffer for service. A pooled customer is transferred to the buffer for service at a service completion epoch with probability p if the inventory exceeds s+1 and provided the number of customers in the buffer is less than the number items held in the inventory. It is assumed that initially the inventory level is S. When inventory level reaches s an order for replenishment is placed. The lead time is exponentially distributed with parameter β. When at least one customer is available in the buffer then reneging will be occurred with parameter 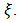 We obtain the steady state analysis is made. Some performance measures are obtained and a few numerical illustrations are provided.
We obtain the steady state analysis is made. Some performance measures are obtained and a few numerical illustrations are provided.
Keywords: Finite buffer customers, Finite pool custom
Cite this paper: Mohammad Ekramol Islam , Rupen Barua , Mohammad Ataullah , Ganesh Chandra Ray , Stochastic Inventory System with Reneging of Customers from the Service Facilities, American Journal of Operational Research, Vol. 10 No. 1, 2020, pp. 8-16. doi: 10.5923/j.ajor.20201001.02.
Article Outline
1. Introduction
- At most of the inventory models it is assumed that the inventory depletes at a rate equal to demand rate. However, it becomes unrealistic for the service facilities where the stocked item is delivered to the customers after some service is performed. In this paper we consider an
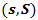 inventory system with service facilities. Arrival of demands form a Poisson process with parameter
inventory system with service facilities. Arrival of demands form a Poisson process with parameter 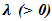 to a buffer of finite capacity equal 0 the inventory level at any given time t. When the maximum buffer size is reached, further demands join a pool of infinite capacity with probability γ or with probability (1- γ) it is lost forever. Pooled customers are taken for service at a service completion epoch if the inventory level is at least s+1. The service time is assumed to be exponentially distributed with parameter μ. It is also assumed that initially the inventory level is S. When inventory level reaches s due to service, an order for replenishment is placed. The lead time is exponentially distributed with parameter. When at least one customer is available in the buffer then reneging will be occurred with parameter
to a buffer of finite capacity equal 0 the inventory level at any given time t. When the maximum buffer size is reached, further demands join a pool of infinite capacity with probability γ or with probability (1- γ) it is lost forever. Pooled customers are taken for service at a service completion epoch if the inventory level is at least s+1. The service time is assumed to be exponentially distributed with parameter μ. It is also assumed that initially the inventory level is S. When inventory level reaches s due to service, an order for replenishment is placed. The lead time is exponentially distributed with parameter. When at least one customer is available in the buffer then reneging will be occurred with parameter 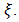 When I(t>B(t) and I(t) ≥s+1 and B(t)= 0, then a pool customer is sent to the buffer with probability p at the previous service epoch. Even when I(t)>B(t) and I(t) < s and B(t)= 0, then there is no pool customers are sent to the buffer. Krishnamoorthy et al [1] analyze retrial production inventory system with service time in which primary demands occur according to Markovian Arrival Process (MAP), using matrix analytic method they carry out the steady state analysis of the system and some performance measures and obtained.Mohammad Ekramol Islam et al [2] developed the reneging concept their paper assuming pool customers can get impatience and can level the pool with probability (1-β) or can enter the pool with probability β that indicate entering customers can have patients to get service.Mohammad Ekramol Islam et al [3] built some inventory models related to postponed demand, reneging pool customers and rejection of customers from the system in service facilities. In that paper they introduce inventory system at service facility with N- policy. Consider reneging and rejection of pool customers. Customers direct go to the pool region and get service.Krishnamoorthy and Mohammad Islam [4] considered and (s, S) inventory system with postponed demands where they assumed that customers arrive to the system according to a Poisson process. When inventory level depletes to s due to demands or decay or service to pool customer, an order for replenishment is placed. The lead-time is exponentially distributed with parameter γ. When inventory level reaches zero, the incoming customers are sent to a pool of capacity M from the pool customers will be picked upfor satisfying demands.Sivakumar and Arivarignan [5] considerd a continuous review perishable inventory system in which the demands arrive according to Morkovian Arrival process (MAP). Berman and Kim [6-7] analyzed a problem in which customers arrive at a service facility according to a Poisson process with service time exponentially distributed and each customer demands one item of the inventory, both zero lead time and positive lead time cases were discussed. Berman and Sapna [8-9] studied and inventory control problem at a service facility, which uses one item of inventory for service provided. They assumed Poisson arrivals, arbitrarily distributed service times and zero lead time and analyze the system with the restriction that the waiting space is finite. Under a specific cost structure, they derived the optimal order quantity that minimizes the long run expected cost rate. The paper is organized as follows:Sections:---------------------------------------------------------------------1. Introduction 2. Mathematical Model2.1. Assumptions2.2. Notations 2.3. The Model build up and analysis2.4. Steady State Analysis2.5. System Performance Measures2.6. Numerical illustration 3. Graphical presentation4. Sensitivity analysis 5. Conclusion. Then we displayed all references cited in the text and the values of the all steady state probability vectors are given in appendix-A.
When I(t>B(t) and I(t) ≥s+1 and B(t)= 0, then a pool customer is sent to the buffer with probability p at the previous service epoch. Even when I(t)>B(t) and I(t) < s and B(t)= 0, then there is no pool customers are sent to the buffer. Krishnamoorthy et al [1] analyze retrial production inventory system with service time in which primary demands occur according to Markovian Arrival Process (MAP), using matrix analytic method they carry out the steady state analysis of the system and some performance measures and obtained.Mohammad Ekramol Islam et al [2] developed the reneging concept their paper assuming pool customers can get impatience and can level the pool with probability (1-β) or can enter the pool with probability β that indicate entering customers can have patients to get service.Mohammad Ekramol Islam et al [3] built some inventory models related to postponed demand, reneging pool customers and rejection of customers from the system in service facilities. In that paper they introduce inventory system at service facility with N- policy. Consider reneging and rejection of pool customers. Customers direct go to the pool region and get service.Krishnamoorthy and Mohammad Islam [4] considered and (s, S) inventory system with postponed demands where they assumed that customers arrive to the system according to a Poisson process. When inventory level depletes to s due to demands or decay or service to pool customer, an order for replenishment is placed. The lead-time is exponentially distributed with parameter γ. When inventory level reaches zero, the incoming customers are sent to a pool of capacity M from the pool customers will be picked upfor satisfying demands.Sivakumar and Arivarignan [5] considerd a continuous review perishable inventory system in which the demands arrive according to Morkovian Arrival process (MAP). Berman and Kim [6-7] analyzed a problem in which customers arrive at a service facility according to a Poisson process with service time exponentially distributed and each customer demands one item of the inventory, both zero lead time and positive lead time cases were discussed. Berman and Sapna [8-9] studied and inventory control problem at a service facility, which uses one item of inventory for service provided. They assumed Poisson arrivals, arbitrarily distributed service times and zero lead time and analyze the system with the restriction that the waiting space is finite. Under a specific cost structure, they derived the optimal order quantity that minimizes the long run expected cost rate. The paper is organized as follows:Sections:---------------------------------------------------------------------1. Introduction 2. Mathematical Model2.1. Assumptions2.2. Notations 2.3. The Model build up and analysis2.4. Steady State Analysis2.5. System Performance Measures2.6. Numerical illustration 3. Graphical presentation4. Sensitivity analysis 5. Conclusion. Then we displayed all references cited in the text and the values of the all steady state probability vectors are given in appendix-A.2. Mathematical Model
2.1. Assumptions
- i. Arrival of demands follows Poisson process with parameter λ.ii. Lead time is exponentially distributed with parameter β.iii. Service time is exponentially distributed with parameterµ.iv. Initially the system is in S.v. Replenishment take place when the inventory level depleted to s.vi. If B (t) = I (t), the primary arrival is directed to the pool with probability γ and with probability (1-γ) it is lost forever.vii. When B(t)= I(t), is the highest inventory level for that situation if perishability occurs immediate one buffer customer must be pull out from buffer.
2.2. Notations
- The notations used in the sequel are explained below: i. I(t) = Inventory level at time t.ii. B (t) = Number of customers in the buffer at time tiii. P(t) = Number of customers in the pool at time tiv.
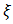 = Reneging ratev. e = Denote the column vector of 1’s
= Reneging ratev. e = Denote the column vector of 1’s2.3. The Model Build Up and Analysis
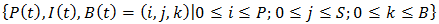 is formed a three dimensional Markov process with state space
is formed a three dimensional Markov process with state space 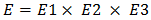 ; where
; where 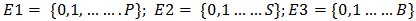 .The infinitesimal generator of the process:
.The infinitesimal generator of the process: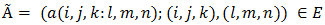 can be obtained using the following arguments:A. The arrival of the demand makes a transition from
can be obtained using the following arguments:A. The arrival of the demand makes a transition from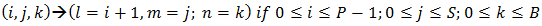 B. The pool customer makes a transition to buffer leaves the pool size less by one as first come first serve basis.
B. The pool customer makes a transition to buffer leaves the pool size less by one as first come first serve basis.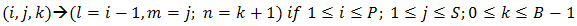 C. For reneging customer from the buffer makes a transition reducing the size of the buffer by one unit.
C. For reneging customer from the buffer makes a transition reducing the size of the buffer by one unit.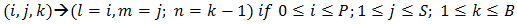 D. If service occurred then a transition reducing the size of the buffer by one unit, as the same time reducing the size of the inventory by one unit.
D. If service occurred then a transition reducing the size of the buffer by one unit, as the same time reducing the size of the inventory by one unit.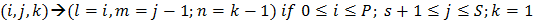 E. Replenishment take place only when inventory less or equal to s
E. Replenishment take place only when inventory less or equal to s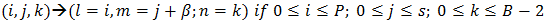 Remark:
Remark: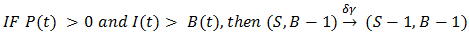 The Infinitesimal generator
The Infinitesimal generator 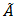 of the three-dimensional Markov Process:
of the three-dimensional Markov Process: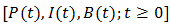 can be defined by The Markov chain
can be defined by The Markov chain 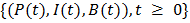 Has the generator
Has the generator 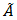 in partitioned from given by
in partitioned from given by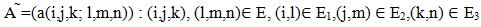 Now, the infinitesimal generator à can be conveniently express as a partition
Now, the infinitesimal generator à can be conveniently express as a partition 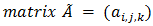 Or,
Or,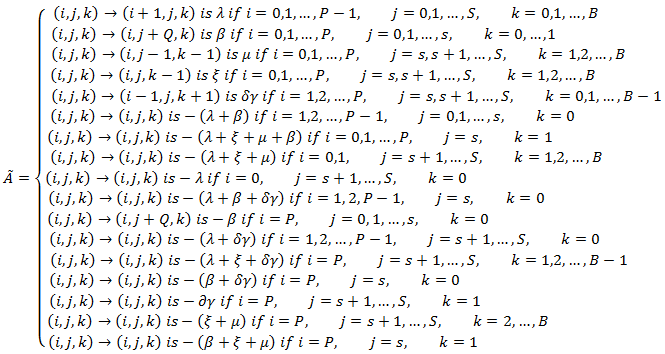
 Where,
Where, 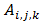 is a
is a 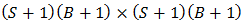 sub-matrix, which is given by
sub-matrix, which is given by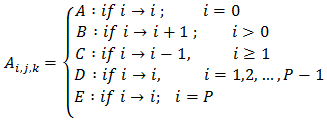 With
With So, we can write the portioned matrix as follows:
So, we can write the portioned matrix as follows: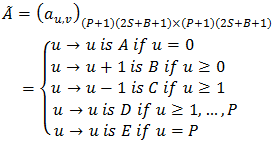
2.4. Steady State Analysis
- It can be seen from the structure of matrixthat the state space
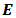 is irreducible. Let the limiting distribution be denoted by
is irreducible. Let the limiting distribution be denoted by 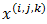
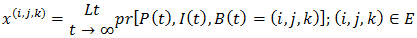 Let
Let 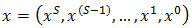 with
with 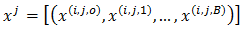 for
for 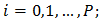
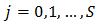 The limiting distribution exists, satisfies the following equation:
The limiting distribution exists, satisfies the following equation: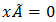 … (1a) and
… (1a) and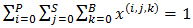 … (1b)The first equation of the above yields a set of equations, which can be represented as a general form in the following manner:
… (1b)The first equation of the above yields a set of equations, which can be represented as a general form in the following manner: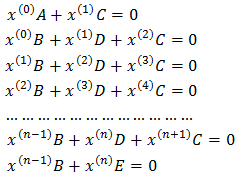 The solution of the above equations (except the last one) can conveniently be expressed as:
The solution of the above equations (except the last one) can conveniently be expressed as: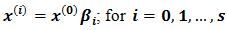 Where
Where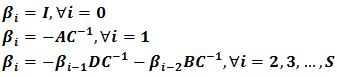 To compute
To compute 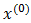 we can use the following equation:
we can use the following equation: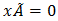 with (1b)(see appendix-B & C)
with (1b)(see appendix-B & C)2.5. System Performance Measures
- In this section we derive some of the system performance measures of the system under consideration:1. Expected Inventory level in the system is,
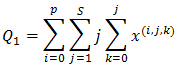 2. Expected number of customers in the buffer is,
2. Expected number of customers in the buffer is,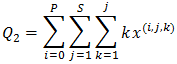 3. Average customers lost to the system is,
3. Average customers lost to the system is,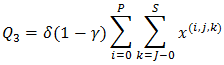 4. Expected number of customers in the pool,
4. Expected number of customers in the pool, 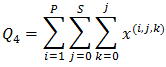 5. Expected number of reneging customer
5. Expected number of reneging customer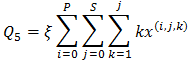 6. Expected re-order level of the system
6. Expected re-order level of the system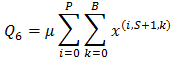 7. Expected rate that a customer will enter the pool is,
7. Expected rate that a customer will enter the pool is,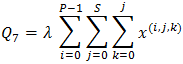 8. The average rate at which the pooling customers will enter the buffer is given by
8. The average rate at which the pooling customers will enter the buffer is given by 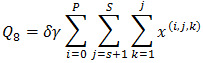
2.6. Cost Function
- Definec1 Inventory holding cost per unit,c2=Cost of buffer customers in the system,c3= Cost of lost customers in the system,c4= Cost of pool customer in the system,c5=Cost of customer reneging to the system,c6= Cost of re-order of the systemSo the total expected cost of the system isE(TC)= C1Q1+ C2Q2+ C3Q3+ C4Q4+ C5Q5+ C6Q6By using above cost function, we can exploit a lot of interesting feature and can make a sensitivity analysis.
2.7. Numerical Illustration
- By giving values to the underlying parameters we provide some numerical illustrations. Take
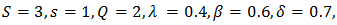
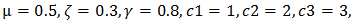
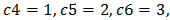 Then we get the measures as described in the table below:
Then we get the measures as described in the table below: | Table 1. Numerical values of different system characteristics |
3. Graphical Presentation
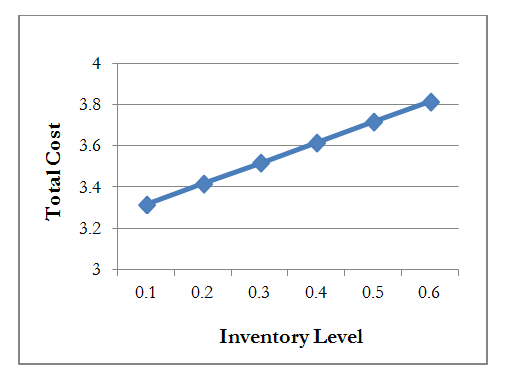 | Graph 1. Inventory Level vs Total Cost |
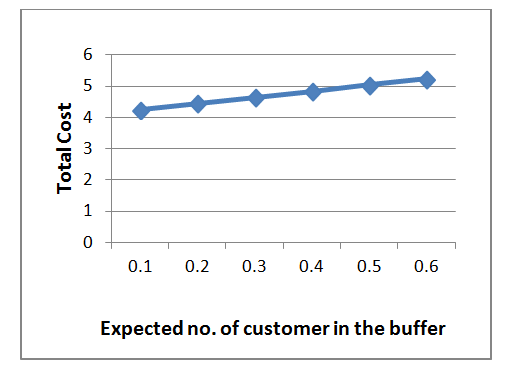 | Graph 2. Expected no. of customer in the buffer vs Total Cost |
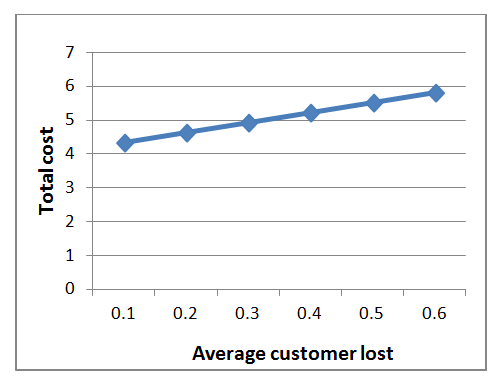 | Graph 3. Average customer Lost vs Total Cost |
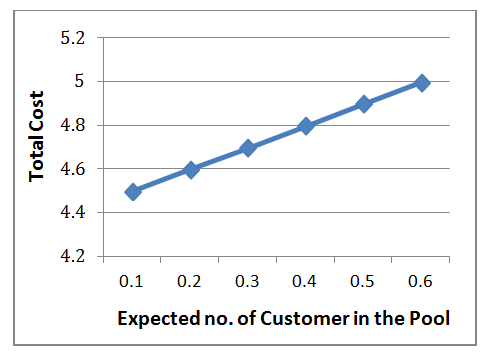 | Graph 4. Expected No. of Customers in the Pool vs Total Cost |
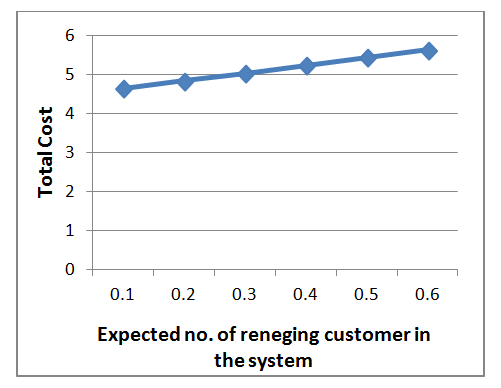 | Graph 5. Expected no. reneging customer in the system vs Total Cost |
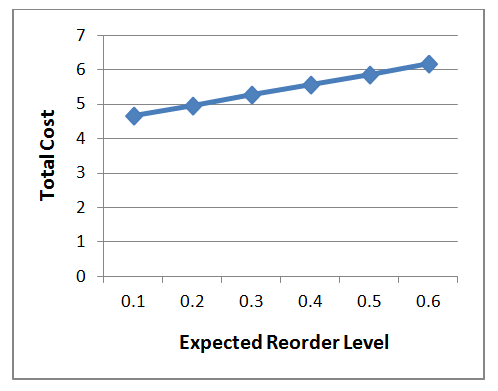 | Graph 6. Expected Reorder Level vs Total Cost |
4. Sensitivity Analysis
- From the graph-1, it is observed that if the inventory level increased then the total cost is increased in significant amount. The result is obvious as the inventory level is increase it has impact on higher re-ordering, lost sales and also increase the cost of carrying pool and buffer customers. Hence the inventory level is vital to this system. From the graph-2, it is observed that expected number of customers in the buffer has a little impact as it increases total cost is increase. From the graph-3, it is observed that average customer lost has a little impact as it increases, total cost is increase. From the graph-4, it is observed that if expected number of customers in the full is increased than the total is measured in a significant amount. From the graph-5, it is observed that if expected of reneging customer has a little impact, as it increases total cost is increased. From the graph-6, it is observed that if expected the re-order level has a little impact, as it increase total cost is increased .Hence it must be scrutinized properly for selection per unit cost for reneging customers.
5. Conclusions
- Generally, inventory models with perishability concept is more complex to analysis than the models where non-perishable items are tackled. The model become more complex, if the perishable rate is depending upon the number of items kept to the stock but sound more realistic. In this present paper, we tackled the same and explored some valuable properties for the model which have a great importance for the management to minimize the total cost.
Appendix-A
Appendix-B
- Theorem: If
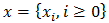 is stationary distribution, then
is stationary distribution, then 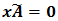 Proof: We have from Kolmogorov forward differential equation
Proof: We have from Kolmogorov forward differential equation 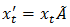
 (a)
(a)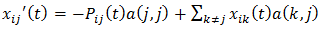
 (b)Since x is stationary then t→∞, if limit exists, it is independent of time parameter and hence
(b)Since x is stationary then t→∞, if limit exists, it is independent of time parameter and hence 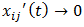 .From equation (a) we get,
.From equation (a) we get, 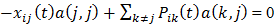 In matrix notation which can be written as
In matrix notation which can be written as 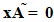 and Normalizing condition hold; then
and Normalizing condition hold; then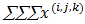 and
and 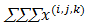 can be completely evaluated. By using the equation (1) with normalizing condition, we calculate all the steady state probability vector by using Mathematic software can be measured.
can be completely evaluated. By using the equation (1) with normalizing condition, we calculate all the steady state probability vector by using Mathematic software can be measured.Appendix-C
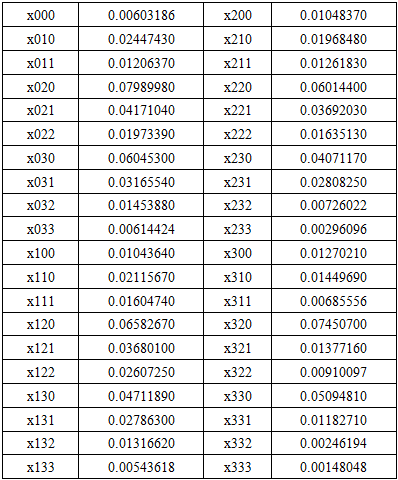
- To solve the equation
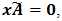 we use the Mathematica Code:Solve[{-1.0x000 + 0x010 + 0.5x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000-1.0x010 + 0.3x011 + 0x020 + 0.5x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010-1.8x011 + 0x020 + 0x021 + 0.5x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0.56x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0.6x000 + 0x010 + 0x011-0.4x020 + 0.3x021 + 0x022 + 0x030 + 0.5x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020-1.2x021 + 0.3x022 + 0x030 + 0x031 + 0.5x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0.56x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021-1.2x022 + 0x030 + 0x031 + 0x032 + 0.5x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0.56x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0.6x010 + 0x011 + 0x020 + 0x021 + 0x022-0.4x030 + 0.3x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0.6x011 + 0x020 + 0x021 + 0x022 + 0x030-1.2x031 + 0.3x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0.56x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031-1.2x032 + 0.3x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0.56x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032-1.2x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0.56x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0.4x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033-1.0x100 + 0x110 + 0.5x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0.4x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100-1.56x110 + 0.3x111 + 0x120 + 0.5x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0.4x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110-1.8x111 + 0x120 + 0x121 + 0.5x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0.56x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0.4x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0.6x100 + 0x110 + 0x111-0.96x120 + 0.3x121 + 0x122 + 0x130 + 0.5x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0.4x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120-1.76x121 + 0.3x122 + 0x130 + 0x131 + 0.5x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0.56x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0.4x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121-1.2x122 + 0x130 + 0x131 + 0x132 + 0.5x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0.56x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0.4x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0.6x110 + 0x111 + 0x120 + 0x121 + 0x122-0.96x130 + 0.3x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0.4x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0.6x111 + 0x120 + 0x121 + 0x122 + 0x130-1.76x131 + 0.3x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0.56x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0.4x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131-1.76x132 + 0.3x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0.56x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0.4x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132-1.2x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0.56x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0.4x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133-1.0x200 + 0x210 + 0.5x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0.4x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200-1.56x210 + 0.3x211 + 0x220 + 0.5x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0.4x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210-1.8x211 + 0x220 + 0x221 + 0.5x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0.56x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0.4x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0.6x200 + 0x210 + 0x211-0.96x220 + 0.3x221 + 0x222 + 0x230 + 0.5x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0.4x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220-1.76x221 + 0.3x222 + 0x230 + 0x231 + 0.5x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0.56x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0.4x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221-1.2x222 + 0x230 + 0x231 + 0x232 + 0.5x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0.56x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0.4x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0.6x210 + 0x211 + 0x220 + 0x221 + 0x222-0.96x230 + 0.3x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0.4x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0.6x211 + 0x220 + 0x221 + 0x222 + 0x230-1.76x231 + 0.3x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0.56x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0.4x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231-1.76x232 + 0.3x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0.56x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0.4x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232-1.2x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0.56x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0.4x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233-0.6x300 + 0x310 + 0.5x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0.4x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300-1.16x310 + 0.3x311 + 0x320 + 0.5x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0.4x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310-1.4x311 + 0x320 + 0x321 + 0.5x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0.4x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0.6x300 + 0x310 + 0x311-0.56x320 + 0.3x321 + 0x322 + 0x330 + 0.5x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0.4x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320-1.36x321 + 0.3x322 + 0x330 + 0x331 + 0.5x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0.4x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321-0.8x322 + 0x330 + 0x331 + 0x332 + 0.5x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0.4x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0.6x310 + 0x311 + 0x320 + 0x321 + 0x322-0.56x330 + 0.3x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0.4x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0.6x311 + 0x320 + 0x321 + 0x322 + 0x330-1.36x331 + 0.3x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0.4x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331-1.36x332 + 0.3x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0.4x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332-0.8x333 = = 0, x000 + x010 + x011 + x020 + x021 + x022 + x030 + x031 + x032 + x033 + x100 + x110 + x111 + x120 + x121 + x122 + x130 + x131 + x132 + x133 + x200 + x210 + x211 + x220 + x221 + x222 + x230 + x231 + x232 + x233 + x300 + x310 + x311 + x320 + x321 + x322 + x330 + x331 + x332 + x333 = = 1}, {x000, x010, x011, x020, x021, x022, x030, x031, x032, x033, x100, x110, x111, x120, x121, x122, x130, x131, x132, x133, x200, x210, x211, x220, x221, x222, x230, x231, x232, x233, x300, x310, x311, x320, x321, x322, x330, x331, x332, x333}]Output:{{x000 = 0.00603186, x010 = 0.0244743, x011 = 0.0120637, x020 = 0.0798998, x021 = 0.0417104, x022 = 0.0197339, x030 = 0.060453, x031 = 0.0316554, x032 = 0.0145388, x033 = 0.00614424, x100 = 0.0104364, x110 = 0.0211567, x111 = 0.0160474, x120 = 0.0658267, x121 = 0.036801, x122 = 0.0260725, x130 = 0.0471189, x131 = 0.027863, x132 = 0.0131662, x133 = 0.00543618, x200 = 0.0104837, x210 = 0.0196848, x211 = 0.0126183, x220 = 0.060144, x221 = 0.0369203, x222 = 0.0163513, x230 = 0.0407117, x231 = 0.0280825, x232 = 0.00726022, x233 = 0.00296096, x300 = 0.0127021, x310 = 0.0144969, x311 = 0.00685556, x320 = 0.074507, x321 = 0.0137716, x322 = 0.00910097, x330 = 0.0509481, x331 = 0.0118271, x332 = 0.00246194, x333 = 0.00148048}}
we use the Mathematica Code:Solve[{-1.0x000 + 0x010 + 0.5x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000-1.0x010 + 0.3x011 + 0x020 + 0.5x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010-1.8x011 + 0x020 + 0x021 + 0.5x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0.56x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0.6x000 + 0x010 + 0x011-0.4x020 + 0.3x021 + 0x022 + 0x030 + 0.5x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020-1.2x021 + 0.3x022 + 0x030 + 0x031 + 0.5x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0.56x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021-1.2x022 + 0x030 + 0x031 + 0x032 + 0.5x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0.56x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0.6x010 + 0x011 + 0x020 + 0x021 + 0x022-0.4x030 + 0.3x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0.6x011 + 0x020 + 0x021 + 0x022 + 0x030-1.2x031 + 0.3x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0.56x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031-1.2x032 + 0.3x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0.56x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032-1.2x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0.56x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0.4x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033-1.0x100 + 0x110 + 0.5x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0.4x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100-1.56x110 + 0.3x111 + 0x120 + 0.5x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0.4x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110-1.8x111 + 0x120 + 0x121 + 0.5x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0.56x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0.4x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0.6x100 + 0x110 + 0x111-0.96x120 + 0.3x121 + 0x122 + 0x130 + 0.5x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0.4x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120-1.76x121 + 0.3x122 + 0x130 + 0x131 + 0.5x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0.56x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0.4x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121-1.2x122 + 0x130 + 0x131 + 0x132 + 0.5x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0.56x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0.4x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0.6x110 + 0x111 + 0x120 + 0x121 + 0x122-0.96x130 + 0.3x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0.4x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0.6x111 + 0x120 + 0x121 + 0x122 + 0x130-1.76x131 + 0.3x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0.56x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0.4x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131-1.76x132 + 0.3x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0.56x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0.4x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132-1.2x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0.56x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0.4x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133-1.0x200 + 0x210 + 0.5x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0.4x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200-1.56x210 + 0.3x211 + 0x220 + 0.5x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0.4x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210-1.8x211 + 0x220 + 0x221 + 0.5x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0.56x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0.4x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0.6x200 + 0x210 + 0x211-0.96x220 + 0.3x221 + 0x222 + 0x230 + 0.5x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0.4x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220-1.76x221 + 0.3x222 + 0x230 + 0x231 + 0.5x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0.56x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0.4x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221-1.2x222 + 0x230 + 0x231 + 0x232 + 0.5x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0.56x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0.4x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0.6x210 + 0x211 + 0x220 + 0x221 + 0x222-0.96x230 + 0.3x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0.4x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0.6x211 + 0x220 + 0x221 + 0x222 + 0x230-1.76x231 + 0.3x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0.56x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0.4x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231-1.76x232 + 0.3x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0.56x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0.4x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232-1.2x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0.56x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0.4x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233-0.6x300 + 0x310 + 0.5x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0.4x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300-1.16x310 + 0.3x311 + 0x320 + 0.5x321 + 0x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0.4x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310-1.4x311 + 0x320 + 0x321 + 0.5x322 + 0x330 + 0x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0.4x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0.6x300 + 0x310 + 0x311-0.56x320 + 0.3x321 + 0x322 + 0x330 + 0.5x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0.4x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320-1.36x321 + 0.3x322 + 0x330 + 0x331 + 0.5x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0.4x222 + 0x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321-0.8x322 + 0x330 + 0x331 + 0x332 + 0.5x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0.4x230 + 0x231 + 0x232 + 0x233 + 0x300 + 0.6x310 + 0x311 + 0x320 + 0x321 + 0x322-0.56x330 + 0.3x331 + 0x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0.4x231 + 0x232 + 0x233 + 0x300 + 0x310 + 0.6x311 + 0x320 + 0x321 + 0x322 + 0x330-1.36x331 + 0.3x332 + 0x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0.4x232 + 0x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331-1.36x332 + 0.3x333 = = 0, 0x000 + 0x010 + 0x011 + 0x020 + 0x021 + 0x022 + 0x030 + 0x031 + 0x032 + 0x033 + 0x100 + 0x110 + 0x111 + 0x120 + 0x121 + 0x122 + 0x130 + 0x131 + 0x132 + 0x133 + 0x200 + 0x210 + 0x211 + 0x220 + 0x221 + 0x222 + 0x230 + 0x231 + 0x232 + 0.4x233 + 0x300 + 0x310 + 0x311 + 0x320 + 0x321 + 0x322 + 0x330 + 0x331 + 0x332-0.8x333 = = 0, x000 + x010 + x011 + x020 + x021 + x022 + x030 + x031 + x032 + x033 + x100 + x110 + x111 + x120 + x121 + x122 + x130 + x131 + x132 + x133 + x200 + x210 + x211 + x220 + x221 + x222 + x230 + x231 + x232 + x233 + x300 + x310 + x311 + x320 + x321 + x322 + x330 + x331 + x332 + x333 = = 1}, {x000, x010, x011, x020, x021, x022, x030, x031, x032, x033, x100, x110, x111, x120, x121, x122, x130, x131, x132, x133, x200, x210, x211, x220, x221, x222, x230, x231, x232, x233, x300, x310, x311, x320, x321, x322, x330, x331, x332, x333}]Output:{{x000 = 0.00603186, x010 = 0.0244743, x011 = 0.0120637, x020 = 0.0798998, x021 = 0.0417104, x022 = 0.0197339, x030 = 0.060453, x031 = 0.0316554, x032 = 0.0145388, x033 = 0.00614424, x100 = 0.0104364, x110 = 0.0211567, x111 = 0.0160474, x120 = 0.0658267, x121 = 0.036801, x122 = 0.0260725, x130 = 0.0471189, x131 = 0.027863, x132 = 0.0131662, x133 = 0.00543618, x200 = 0.0104837, x210 = 0.0196848, x211 = 0.0126183, x220 = 0.060144, x221 = 0.0369203, x222 = 0.0163513, x230 = 0.0407117, x231 = 0.0280825, x232 = 0.00726022, x233 = 0.00296096, x300 = 0.0127021, x310 = 0.0144969, x311 = 0.00685556, x320 = 0.074507, x321 = 0.0137716, x322 = 0.00910097, x330 = 0.0509481, x331 = 0.0118271, x332 = 0.00246194, x333 = 0.00148048}} Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML