1. Introduction

The scalarizing technique was first introduced in year 1983 [1] for solving MOO problems. The technique has been successfully used for resource use planning in agriculture for increasing farm income, increasing farm employment with lesser use of fertilizer, irrigation etc. [2] [3]..[10]. Several new averaging techniques [11] [12]… [27] using mean, harmonic mean and geometric mean have been proposed during last three decades. Most of these scalarizing techniques have been found inefficient in generating the acceptable MOO solutions [28] [29]. The improved scalarizing techniques are proposed for generating compromising and acceptable solutions of MOO problems.

2. Multi-Objective Optimization Problem

For optimizing ‘n’ objective functions with maximization of ‘r’ objective functions and minimization of remaining ‘n-r’ objective functions. The MOO problem is formulated as described below:

Optimize Z = [Max.Z₁,Z₂…….Z_r, Min. Z_r+1,……..Z_n]

Where,

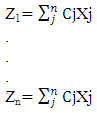Subject To:

AX = b and X ≥ 0

2.1. Existing Scalarizing Techniques

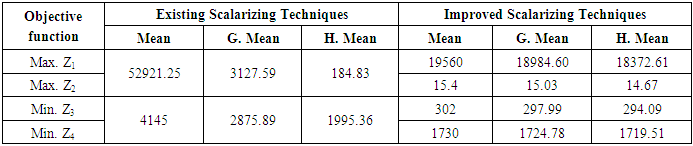
There are many scalarizing techniques for solving MOO problems. The scalarizing techniques using mean, geometric mean and harmonic mean have been explained with an example. The multi-objective function is constructed by scalarizing each objective function by the mean, geometric and harmonic mean of optimal values of objective functions as described below:

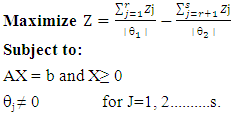Where,

│θ₁│= Mean, Geometric Mean and Harmonic Mean of optimal values of maximization objective functions.

│θ₂│= Mean, Geometric Mean and Harmonic Mean of optimal values of Minimization Objective functions.

Note: The estimation of θ₁ and θ₂ is not logical when objective functions are of different dimensions.

2.2. Improved Scalarizing Techniques

The multi-objective function is constructed as explained below:

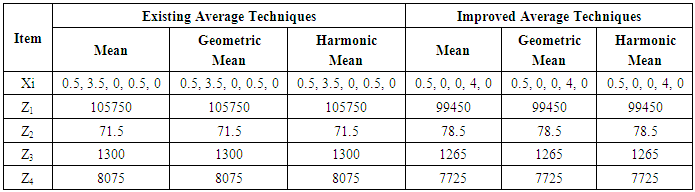
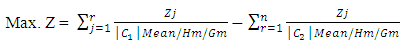Where,

│C₁│ = Mean, Harmonic mean (Hm) or Geometric mean (Gm) of C_j values of Maximization objective functions

│C₂│ = Mean, Harmonic mean (Hm) or Geometric mean (Gm) of C_j values of Minimization objective functions

Note: The multi-objective function is free from the problem of multi dimensions aggregation.

3. Solving MOO Problem

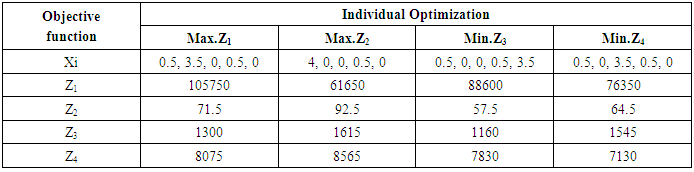
Example

The following example for achieving four objective functions has been solved using both existing and improved scalarizing techniques.

Max. Z₁ = 12500X₁ + 25100X₂ + 16700X₃ + 23300X₄ + 20200X₅

Max. Z₂ = 21X₁ + 15X₂ +13X₃ + 17X₄ + 11X₅

Min. Z₃ = 370X₁ + 280X₂ + 350X₃ +270X₄ + 240X₅

Min. Z₄ = 1930X₁ + 1790X₂ + 1520X₃ + 1690X₄ + 1720X₅

Subject to:

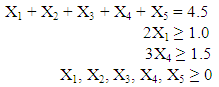All the objective functions have been optimized individually and the solution is presented in Table 1.

Table 1. Individual Optimization

It is very clear that all the four individual optimizations are all different and conflicting to each other. The value of first objective function is 1, 05,750 which is highest among other values of same objective function. Similarly the value of second objective function is also highest and values of third and fourth objective functions are lowest as desired. This conflicting scenario necessitates the need for multi-objective optimization.

The mean, geometric mean and harmonic mean have been used for scalarizing the multi-objective function. The mean, geometric mean and harmonic mean have been estimated for both existing and improved techniques of scalarizing as given in Table 2.

Table 2. Mean, Geometric Mean and Harmonic Mean

The mean, geometric mean and harmonic mean of maximum values of objective functions Z₁ and Z₂ are 52921.25, 3127.59 and 184.83 respectively as given in Table 2. Similarly the mean, geometric mean and harmonic mean of minimum values of remaining objective functions 3 and 4 are 4145, 2875.89 and 1995.3 respectively for existing scalarizing techniques. On the other hand, for improved scalarizing techniques, the mean, geometric mean and harmonic mean have been estimated considering all the four (one optimal and three sub optimal) values of each objective function as mentioned in Table 2. The multi-objective function has been formulated by scalarizing the objective functions using mean, geometric mean and harmonic mean as explained in equations 2.1 and 2.2. The existing and improved scalarized multi-objective functions have been optimized and the results are presented in Table 3.

Table 3. Multi-Objective Optimization

The Table 3 indicates that all the three scalarized multi-objective functions generated unique solution. These solutions are same as individual optimum of objective function Z₁. The existing scalarizing techniques are unable to generate the compromising solution. However, the improved scalarizing techniques have optimized all the objective functions simultaneously. The value of each objective function is closer to its individual optimum as given in Table 1. The optimal solutions generated by improved scalarizing techniques are compromising and acceptable.

4. Conclusions

There are several scalarizing techniques used for solving MOO problems. The mean, geometric mean and harmonic mean have been frequently used for scalarizing the objective functions. The solutions of MOO problems generated using these techniques were not superior. However the improved scalarizing techniques using mean, harmonic mean and geometric mean are found superior and efficient in solving MOO problems for obtaining compromising solutions.