Subhash Kumar Yadav 1, S. S. Mishra 1, Alok Kumar Shukla 2, Shakti Kumar 3, Ram Sagar Singh 4
1Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India
2Department of Statistics, D.A.V College, Kanpur, U.P., India
3Centre for Economic Studies and Planning, School of Social Sciences, Jawaharlal Nehru University, New Delhi, India
4Kamla Nehru Institute of Management & Engineering, Dr APJ Abdul Kalam Technical University, India
Correspondence to: S. S. Mishra , Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we have proposed some improved modified ratio type estimators for population mean of study variable using auxiliary information in the form of non-conventional measures of dispersion Gini’s mean difference, Downton’s method and probability weighted moments given by Abid (2016) with linear combination of population coefficient of Skewness and Kurtosis of auxiliary variable. The large sample properties of the proposed estimators have been studied up to the first order of approximation that is the biases and the mean squared errors. A comparison has been made with the existing estimators of population mean. The conditions under which the proposed estimators perform better than the other existing estimators have been mentioned. An empirical study is also carried out to justify the theoretical findings. The theoretical as well as the empirical findings show the improvement of the proposed estimators over other existing estimators for the estimation of population mean.
Keywords:
Study variable, Auxiliary variable, Bias, Mean Squared Error, Efficiency
Cite this paper: Subhash Kumar Yadav , S. S. Mishra , Alok Kumar Shukla , Shakti Kumar , Ram Sagar Singh , Use of Non-Conventional Measures of Dispersion for Improved Estimation of Population Mean, American Journal of Operational Research, Vol. 6 No. 3, 2016, pp. 69-75. doi: 10.5923/j.ajor.20160603.03.
1. Introduction
Whenever the population is large, it is very time taking and costly to get the information on each of the population unit. Sampling is a very good alternative to overcome this problem. It is very natural to estimate any parameter of the population by its corresponding statistic. Thus to estimate the population mean, the most appropriate estimator is the sample mean. The sample mean is unbiased, but it seems to have large amount of variation. Now our aim is to seek an estimator which may be biased but it should have lesser mean squared error as compared to sample mean. The use of auxiliary information supplied by the auxiliary variable fulfills our aim to find more and more efficient estimators. The auxiliary variable is the variable about which the experimenter has full information and it is collected with the main variable under study without increasing the cost of the survey. The auxiliary variable may be positively or negatively correlated with the study variable under consideration. When the auxiliary variable has positive relationship with the main variable under study and the line of regression of y on x passes through origin, ratio type estimators are used to estimate population parameters under consideration. When it has negative relationship with the main variable under study, product type estimators are used otherwise regression type estimators are used for the estimation of parameters under investigation. In the present study, we have considered the positive correlation case only so only ratio type estimators are studied along with the proposed ratio type class of estimators. Let the finite population of interest consist of N distinct and identifiable units and let 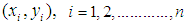 be a bivariate sample of size n taken from (X, Y) using a SRSWOR scheme. Let
be a bivariate sample of size n taken from (X, Y) using a SRSWOR scheme. Let 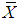 and
and 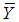 respectively be the population means of the auxiliary and the study variables, and let
respectively be the population means of the auxiliary and the study variables, and let 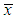 and
and 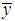 be the corresponding sample means which are unbiased estimators of
be the corresponding sample means which are unbiased estimators of 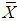 and
and 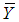 respectively. Let
respectively. Let 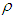 be the correlation coefficient between X and Y.
be the correlation coefficient between X and Y.
2. Notations
Following notations have been used in this manuscript,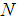 - Size of the population
- Size of the population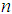 - Size of the sample
- Size of the sample 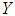 - Study variable
- Study variable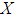 - Auxiliary variable
- Auxiliary variable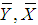 - Population means
- Population means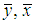 - Sample means
- Sample means 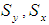 - Population Standard Deviations
- Population Standard Deviations 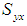 - Population Covariance between Y and X
- Population Covariance between Y and X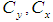 - Coefficients of Variation
- Coefficients of Variation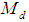 - Median of the auxiliary variable
- Median of the auxiliary variable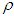 - Correlation coefficient between X and Y
- Correlation coefficient between X and Y 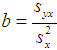 - Regression coefficient of y on x
- Regression coefficient of y on x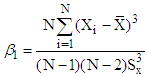 - Coefficient of Skewness of auxiliary variable
- Coefficient of Skewness of auxiliary variable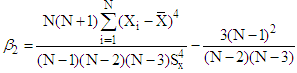 - Coefficient of Kurtosis of auxiliary variable
- Coefficient of Kurtosis of auxiliary variable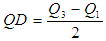 - Quartile Deviation
- Quartile Deviation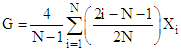 - Gini’s Mean Difference
- Gini’s Mean Difference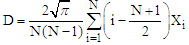 - Downton’s Parameters
- Downton’s Parameters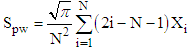 - Probability Weighted Moments
- Probability Weighted Moments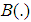 - Bias of the estimator
- Bias of the estimator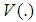 - Variance of the estimator
- Variance of the estimator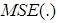 - Mean squared error of the estimator
- Mean squared error of the estimator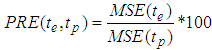 - Percentage relative efficiency of the estimator
- Percentage relative efficiency of the estimator 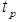 over
over 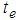
3. Review of Existing Estimators
As mentioned above the most appropriate estimator for population mean 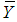 is the sample mean
is the sample mean 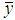 that is mean per unit estimator given by,
that is mean per unit estimator given by,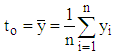 It is an unbiased estimator of population mean and its variance up to the first order of approximation is,
It is an unbiased estimator of population mean and its variance up to the first order of approximation is,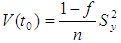 | (1) |
Cochran (1940) keeping in mind that the mean per unit estimator has sufficiently large variance, used the auxiliary variable to estimate the population mean of the main variable and proposed the traditional ratio estimator as,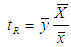 It is a biased estimator of population mean and its bias and mean squared error, up to the first order of approximation respectively are,
It is a biased estimator of population mean and its bias and mean squared error, up to the first order of approximation respectively are,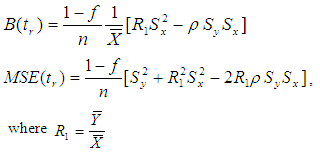 | (2) |
Kadilar and Cingi (2004) suggested some improved ratio type estimators of population mean as,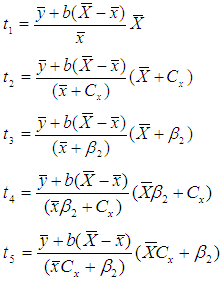 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 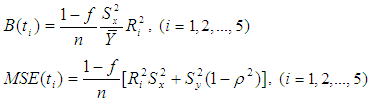 | (3) |
Where, 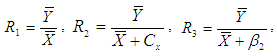
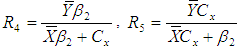 Kadilar and Cingi (2006) suggested some more improved ratio type estimators of population mean as,
Kadilar and Cingi (2006) suggested some more improved ratio type estimators of population mean as,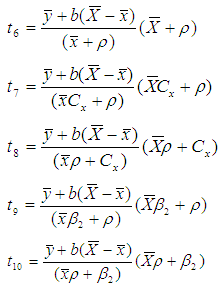 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 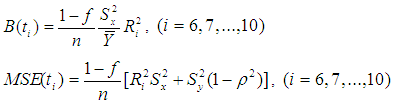 | (4) |
Where, 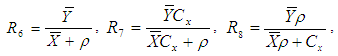
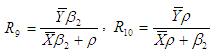 Yan and Tian (2010) suggested two modified ratio type estimators of population mean using information on auxiliary variable in the form of coefficient of skewness and kurtosis respectively as,
Yan and Tian (2010) suggested two modified ratio type estimators of population mean using information on auxiliary variable in the form of coefficient of skewness and kurtosis respectively as, 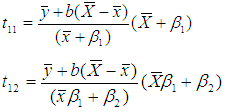 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 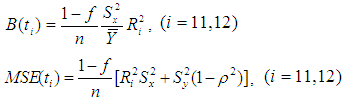 | (5) |
Where, 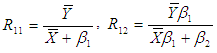 Subramani and Kumarpandiyan (2012a, 2012b, 2012c) suggested some modified improved ratio type estimators of population mean using median with coefficient of skewness, kurtosis and coefficient of variation as,
Subramani and Kumarpandiyan (2012a, 2012b, 2012c) suggested some modified improved ratio type estimators of population mean using median with coefficient of skewness, kurtosis and coefficient of variation as, 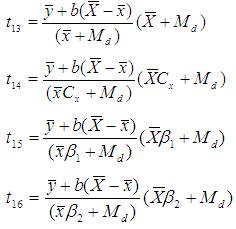 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 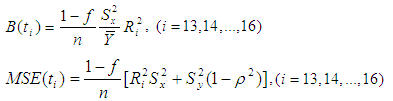 | (6) |
Where, 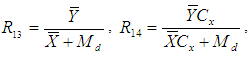
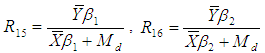 Jeelani et al. (2013) suggested the following modified ratio type estimator of population mean using coefficient of skewness and quartile difference of auxiliary variable as,
Jeelani et al. (2013) suggested the following modified ratio type estimator of population mean using coefficient of skewness and quartile difference of auxiliary variable as, 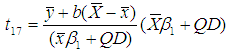 The bias and the mean squared error of above estimator, up to the first order of approximation is given by,
The bias and the mean squared error of above estimator, up to the first order of approximation is given by, 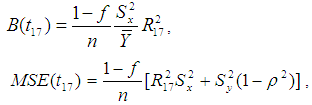 | (7) |
Where, 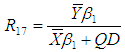 Abid et al. (2016) introduced some modified improved estimators of population mean using some non-conventional parameters of auxiliary variable as,
Abid et al. (2016) introduced some modified improved estimators of population mean using some non-conventional parameters of auxiliary variable as, 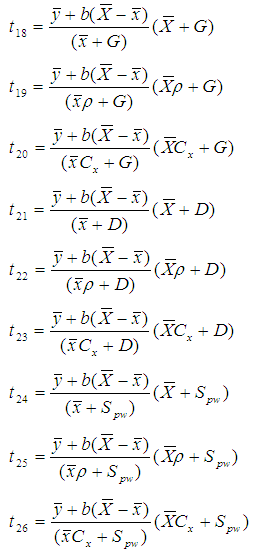 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 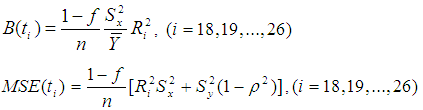 | (8) |
where, 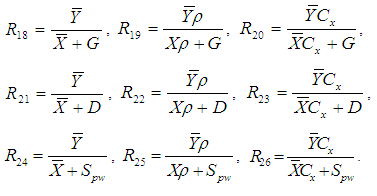
4. Proposed Estimators
Motivated by Abid et al. (2016) and Subramani (2013), we have proposed the following improved modified ratio type estimators of population mean using specific parameter of auxiliary variable along with the non-conventional parameters of auxiliary variable as, 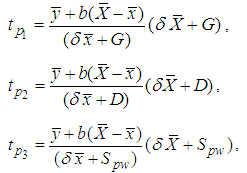 Where,
Where, 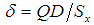 . The biases and the mean squared errors of proposed estimators, up to the first order of approximations respectively can be obtained as,
. The biases and the mean squared errors of proposed estimators, up to the first order of approximations respectively can be obtained as, 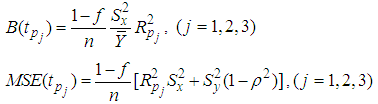 | (9) |
Where, 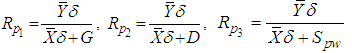
5. Efficiency Comparison
In this section, we have compared theoretically the proposed estimator with the existing estimators of population mean and have given the conditions under which the proposed estimator performs better than the other estimators of population mean under simple random sampling without replacement scheme. 5(a). Comparison with mean per unit estimatorFrom equation (9) and equation (2), we see that the proposed estimators are better than the mean per unit estimator if, 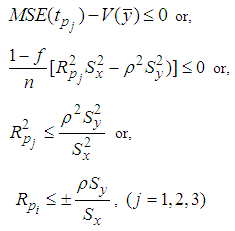 | (10) |
5(b). Comparison with usual ratio estimatorThe proposed estimators are better than the usual ratio estimator if, 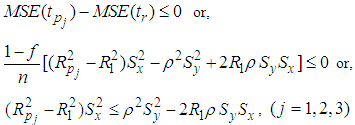 | (11) |
5(c). Comparison with Kadilar and Cingi (2004) estimatorsFrom equation (9) and equation (3), the proposed estimators are better than the Kadilar and Cingi (2004) estimators if, 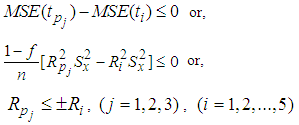 | (12) |
5(d). Comparison with Kadilar and Cingi (2006) estimatorsFrom equation (9) and equation (4) it is seen that the proposed estimators are better than the Kadilar and Cingi (2006) estimators under the conditions if, 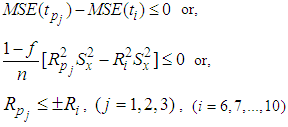 | (13) |
5(e). Comparison with Yan and Tian (2010) estimatorsThe proposed estimators are better than Yan and Tian (2010) estimators if, 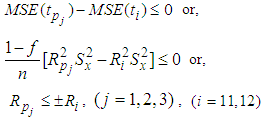 | (14) |
5(f). Comparison with Subramani and Kumarpandiyan (2012a, 2012b, 2012c) estimatorsFrom equation (9) and equation (6) it is seen that the proposed estimators are better than Subramani and Kumarpandiyan (2012a, 2012b, 2012c) estimators under the conditions if, 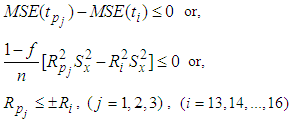 | (15) |
5(g). Comparison with Jeelani et al. (2013) estimatorThe proposed estimators are better than Jeelani et al. (2013) estimator if, 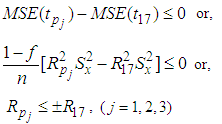 | (16) |
5(h). Comparison with Abid et al. (2016) estimatorsFrom equation (9) and equation (6) it is seen that the proposed estimators are better than Abid et al. (2016) estimators under the conditions if, 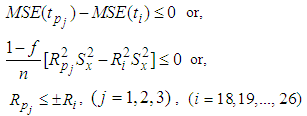 | (17) |
6. Numerical Illustration
In this section, we have used the data of Kadilar and Cingi (2004). They have considered the data of only Aegean Region of Turkey under simple random sampling scheme. We have applied our proposed and other ratio type estimators for the data on amount of apple production (as study variable) and number of apple trees (as auxiliary variable) in 106 villages of Aegean Region in 1999. Using these data we have computed MSE of proposed estimators along with the other ratio type estimators mentioned in this manuscript and these estimators are compared with each other with respect to their MSE values.We observe the statistics about the population. It is worth notable that the correlation between the study and the auxiliary variable is 86% and we have taken a sample of size n = 40. It would be important to mention that the sample size has no effect on the efficiency comparisons of the estimators.The population parameters for the above data are,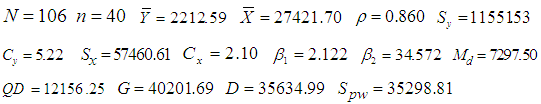
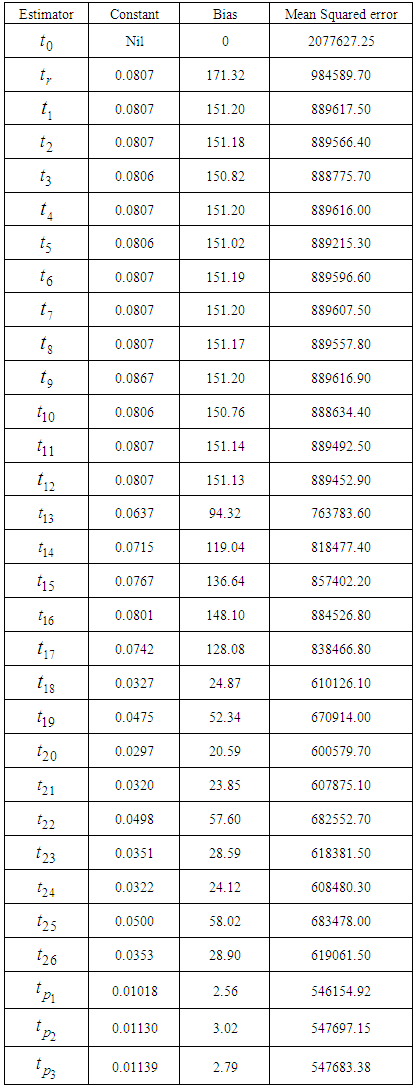
Table 1. Constants, Biases and MSE of Proposed and other estimators
 |
| |
|
The values of the related constants, biases and the mean squared error of the existing and proposed improved ratio estimators are given in Table-1.
7. Results and Conclusions
In this manuscript we have proposed an improved estimator of population mean using a special parameter of auxiliary variable along with some non-traditional measures of dispersion of auxiliary variable. The expressions for the bias and mean squared error have been obtained up to the first order of approximation. A theoretical as well as numerical comparison of proposed estimators has been made with other existing estimators of population mean. From the above Table-1, it can be observed that the related constants, biases and mean squared errors of the proposed improved ratio type estimators are smaller than the usual ratio estimator and the other existing ratio estimators in literature. Thus the proposed estimators perform better than the usual ratio estimator and the other existing modified ratio estimators in terms of MSE, which indicates that the proposed estimators are more efficient. Therefore it is recommended that the proposed estimators may be used for the efficient estimation of population mean. It can be further noted that among the proposed estimators the estimator 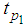 performs better than the other two proposed estimators.
performs better than the other two proposed estimators.
References
| [1] | Abid, M., Abbas, N., Sherwani, R.A.K. and Nazir, H.Z. (2016). Improved Ratio Estimators for the Population Mean Using Non-Conventional Measures of Dispersion, Pakistan Journal of Statistics and Operations Research, XII, 2, 353-367. |
| [2] | Cochran, W. G. (1940). Sampling Techniques, Third Edition, Wiley Eastern Limited. |
| [3] | Jeelani, M. I. Maqbool, S. and Mir, S. A. (2013). Modified ratio estimators of population mean using linear combination of coefficient of skewness and quartile deviation. International Journal of Modern Mathematical Sciences, (6), 174–183. |
| [4] | Kadilar, C. and Cingi, H. (2004). Ratio estimators in simple random sampling. Applied Mathematics and Computation, 151, 893-902. |
| [5] | Kadilar, C. and Cingi, H. (2006). An Improvement in estimating the population mean by using the correlation coefficient, Hacettepe Journal of Mathematics and Statistics, 35 (1), 103-109. |
| [6] | Subramani, J. (2013). Generalized Modified Ratio Estimator for Estimation of Finite Population Mean, Journal of Modern Applied Statistical Methods, 12, 2, 121-155. |
| [7] | Subramani, J. and Kumarapandiyan, G. (2012a). Estimation of Population Mean using Co-efficient of variation and Median of an Auxiliary Variable. International Journal of Probability and Statistics, (1), 111–118. |
| [8] | Subramani, J. and Kumarapandiyan, G. (2012b). Estimation of population mean using known median and co-efficient of skewness. American Journal of Mathematics and Statistics, (2), 101-107. |
| [9] | Subramani, J. and Kumarapandiyan, G. (2012c). Modified ratio estimators using known median and co-efficient of kurtosis. American Journal of Mathematics and Statistics, (2), 95–100. |
| [10] | Yan, Z. and Tian, B. (2010): Ratio method to the mean estimation using coefficient of skewness of auxiliary variable, ICICA 2010, Part II, CCIS 106, 103–110. |



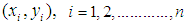 be a bivariate sample of size n taken from (X, Y) using a SRSWOR scheme. Let
be a bivariate sample of size n taken from (X, Y) using a SRSWOR scheme. Let  and
and 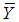 respectively be the population means of the auxiliary and the study variables, and let
respectively be the population means of the auxiliary and the study variables, and let 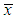 and
and 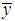 be the corresponding sample means which are unbiased estimators of
be the corresponding sample means which are unbiased estimators of 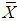 and
and 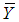 respectively. Let
respectively. Let 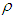 be the correlation coefficient between X and Y.
be the correlation coefficient between X and Y. 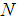 - Size of the population
- Size of the population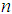 - Size of the sample
- Size of the sample 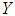 - Study variable
- Study variable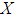 - Auxiliary variable
- Auxiliary variable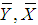 - Population means
- Population means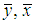 - Sample means
- Sample means 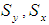 - Population Standard Deviations
- Population Standard Deviations 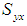 - Population Covariance between Y and X
- Population Covariance between Y and X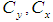 - Coefficients of Variation
- Coefficients of Variation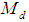 - Median of the auxiliary variable
- Median of the auxiliary variable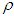 - Correlation coefficient between X and Y
- Correlation coefficient between X and Y 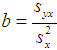 - Regression coefficient of y on x
- Regression coefficient of y on x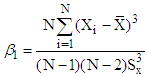 - Coefficient of Skewness of auxiliary variable
- Coefficient of Skewness of auxiliary variable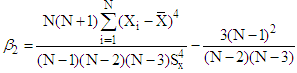 - Coefficient of Kurtosis of auxiliary variable
- Coefficient of Kurtosis of auxiliary variable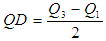 - Quartile Deviation
- Quartile Deviation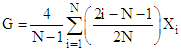 - Gini’s Mean Difference
- Gini’s Mean Difference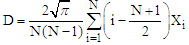 - Downton’s Parameters
- Downton’s Parameters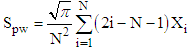 - Probability Weighted Moments
- Probability Weighted Moments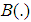 - Bias of the estimator
- Bias of the estimator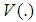 - Variance of the estimator
- Variance of the estimator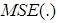 - Mean squared error of the estimator
- Mean squared error of the estimator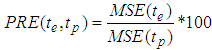 - Percentage relative efficiency of the estimator
- Percentage relative efficiency of the estimator 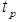 over
over 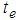
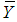 is the sample mean
is the sample mean 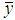 that is mean per unit estimator given by,
that is mean per unit estimator given by,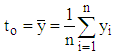 It is an unbiased estimator of population mean and its variance up to the first order of approximation is,
It is an unbiased estimator of population mean and its variance up to the first order of approximation is,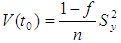
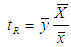 It is a biased estimator of population mean and its bias and mean squared error, up to the first order of approximation respectively are,
It is a biased estimator of population mean and its bias and mean squared error, up to the first order of approximation respectively are,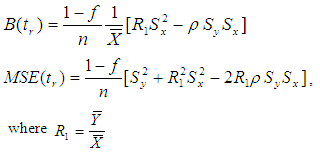
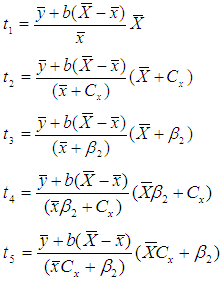 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 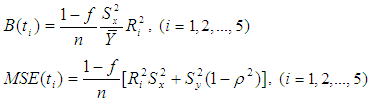
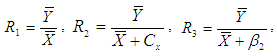
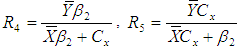 Kadilar and Cingi (2006) suggested some more improved ratio type estimators of population mean as,
Kadilar and Cingi (2006) suggested some more improved ratio type estimators of population mean as,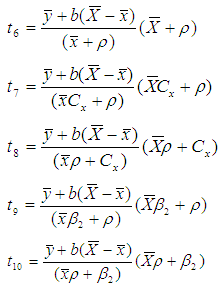 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 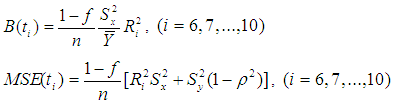
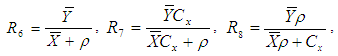
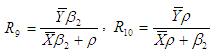 Yan and Tian (2010) suggested two modified ratio type estimators of population mean using information on auxiliary variable in the form of coefficient of skewness and kurtosis respectively as,
Yan and Tian (2010) suggested two modified ratio type estimators of population mean using information on auxiliary variable in the form of coefficient of skewness and kurtosis respectively as, 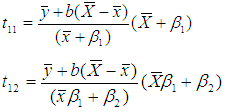 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 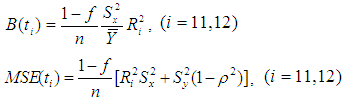
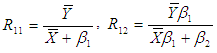 Subramani and Kumarpandiyan (2012a, 2012b, 2012c) suggested some modified improved ratio type estimators of population mean using median with coefficient of skewness, kurtosis and coefficient of variation as,
Subramani and Kumarpandiyan (2012a, 2012b, 2012c) suggested some modified improved ratio type estimators of population mean using median with coefficient of skewness, kurtosis and coefficient of variation as, 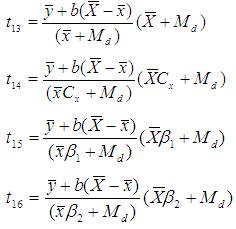 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 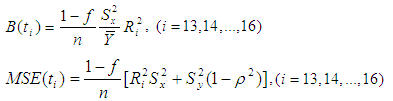
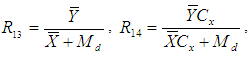
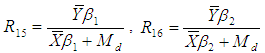 Jeelani et al. (2013) suggested the following modified ratio type estimator of population mean using coefficient of skewness and quartile difference of auxiliary variable as,
Jeelani et al. (2013) suggested the following modified ratio type estimator of population mean using coefficient of skewness and quartile difference of auxiliary variable as, 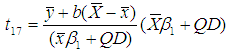 The bias and the mean squared error of above estimator, up to the first order of approximation is given by,
The bias and the mean squared error of above estimator, up to the first order of approximation is given by, 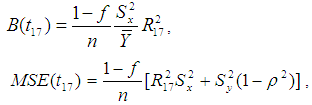
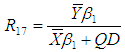 Abid et al. (2016) introduced some modified improved estimators of population mean using some non-conventional parameters of auxiliary variable as,
Abid et al. (2016) introduced some modified improved estimators of population mean using some non-conventional parameters of auxiliary variable as, 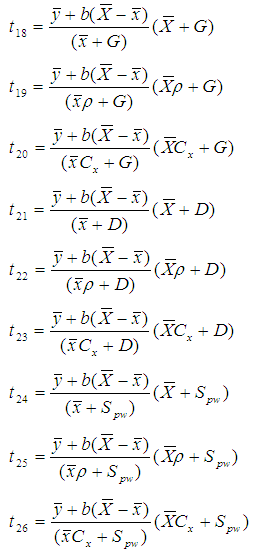 The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are,
The biases and the mean squared errors of above estimators, up to the first order of approximations respectively are, 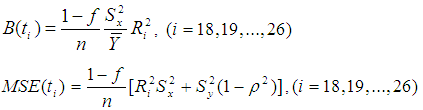
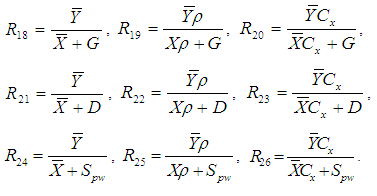
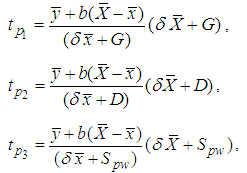 Where,
Where, 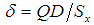 . The biases and the mean squared errors of proposed estimators, up to the first order of approximations respectively can be obtained as,
. The biases and the mean squared errors of proposed estimators, up to the first order of approximations respectively can be obtained as, 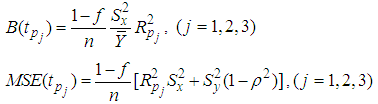
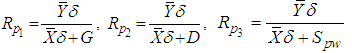
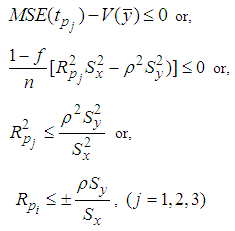
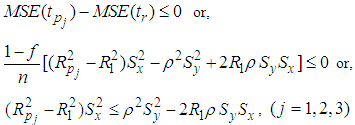
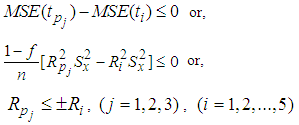
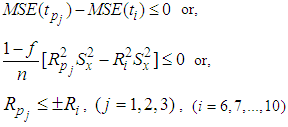
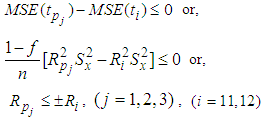
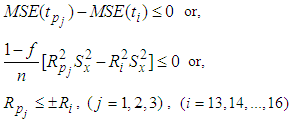
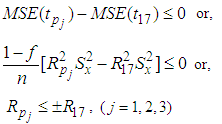
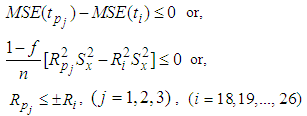
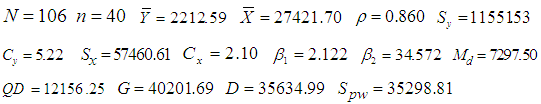
 performs better than the other two proposed estimators.
performs better than the other two proposed estimators.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML