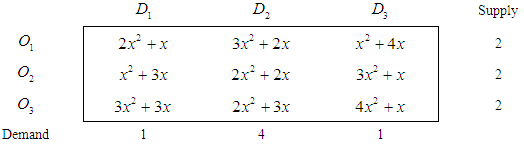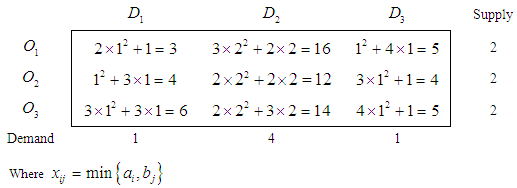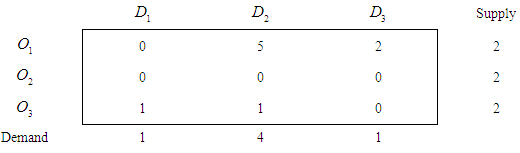Shambhu Sharma1, Rama Shanker2, Ravi Shanker3
1Department of Mathematics, Dayalbagh Educational Institute, Dayalbagh, Agra, India
2Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
3Department of Mathematics, G.L.A. College, N.P. University, Daltonganj, Jharkhand, India
Correspondence to: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In the present paper, a maximin zero suffix method introduced by Sharma et al (2014) has been extended to solve the quadratic transportation problem (QTP). The proposed method is better than the existing methods in the literature for solving QTP because it is free from any huge algebraic computation and drawing of graphs of quadratic cost functions to search absolute point. The algorithm of the proposed method has been given and a numerical example has been presented to explain its application. The proposed method is very simple, easy to understand and apply for any practitioners who have not much knowledge of mathematics.
Keywords:
Quadratic transportation problem, Estimated cost matrix, Transformed cost matrix, Reduced cost matrix, Zero suffix method, Optimal solution
Cite this paper: Shambhu Sharma, Rama Shanker, Ravi Shanker, A Maximin Zero Suffix Method for Quadratic Transportation Problem, American Journal of Operational Research, Vol. 6 No. 3, 2016, pp. 55-60. doi: 10.5923/j.ajor.20160603.01.
1. Introduction
The classical transportation problem (CTP) is a particular class of linear programming problem (LPP) and deals with the distribution of goods (or products) from m sources (plants or suppliers) to n destinations (warehouses or customers). The main objective in CTP is to determine the amount of goods to be shipped from each source to each destination so as to maintain the demand and supply requirements at the minimum total transportation cost. In CTP, the cost of transporting one unit of goods from a source to a destination is independent of the amount of goods shipped. The classical transportation problem (CTP) is defined as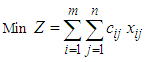
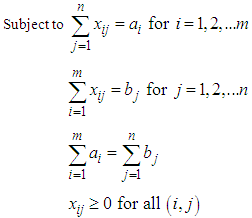 where
where 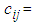 Unit transportation cost from
Unit transportation cost from 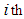 source to
source to 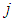 th destination
th destination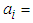 Amount of goods available at th source.
Amount of goods available at th source.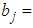 Amount of goods required at th destination
Amount of goods required at th destination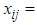 Amount of goods transported from th source to
Amount of goods transported from th source to 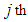 destination.
destination.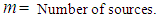
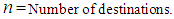 CTP, being a well structured problem, has been studied extensively in the literature. It was Hitchcock (1941) who firstly developed the basic transportation problem and suggested constructive method of solution. Later on, Dantzig (1963) formulated the CTP as an LPP and provided the solution. A number of researchers have worked to find suitable methods of solving CTP using different assumptions including Charnes and Cooper (1954), Shih (1987), Arsham and Khan (1989), Adlakha and Kowalski (1999), Ji and Chu (2002), Korukoglu and Balli (2011), Sudhakar et al (2012), are some among others. Recently Sharma et al (2013) have introduced an easy and interesting method named, “A modified zero suffix method” for finding optimal solution for CTP.In the real life situation, per unit transportation cost of goods does not remain always constant. Generally, it decreases with the increase in the volume of transported goods but not always. Sometimes, it has also been seen that it increases with the increase in the volume of the transported goods due to highway congestion (restriction of over loading). This idea leads to a new dimension of the CTP and generally it has been observed that per unit cost
CTP, being a well structured problem, has been studied extensively in the literature. It was Hitchcock (1941) who firstly developed the basic transportation problem and suggested constructive method of solution. Later on, Dantzig (1963) formulated the CTP as an LPP and provided the solution. A number of researchers have worked to find suitable methods of solving CTP using different assumptions including Charnes and Cooper (1954), Shih (1987), Arsham and Khan (1989), Adlakha and Kowalski (1999), Ji and Chu (2002), Korukoglu and Balli (2011), Sudhakar et al (2012), are some among others. Recently Sharma et al (2013) have introduced an easy and interesting method named, “A modified zero suffix method” for finding optimal solution for CTP.In the real life situation, per unit transportation cost of goods does not remain always constant. Generally, it decreases with the increase in the volume of transported goods but not always. Sometimes, it has also been seen that it increases with the increase in the volume of the transported goods due to highway congestion (restriction of over loading). This idea leads to a new dimension of the CTP and generally it has been observed that per unit cost 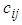 is a function of the amount shipped
is a function of the amount shipped 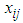 . If the per unit transportation cost
. If the per unit transportation cost 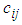 in CTP is a quadratic function
in CTP is a quadratic function 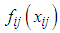 of
of 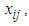 then CTP is termed as the quadratic transportation problem (QTP). In QTP, the cost coefficients are quadratic functions, and in CTP the cost coefficients are constants.Mathematically, the quadratic transportation problem (QTP) is defined as
then CTP is termed as the quadratic transportation problem (QTP). In QTP, the cost coefficients are quadratic functions, and in CTP the cost coefficients are constants.Mathematically, the quadratic transportation problem (QTP) is defined as 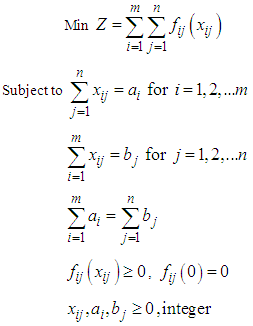 There is no any efficient direct algorithm to solve QTP in the literature. However, QTP and its indirect solution techniques have been discussed by researchers including Hochbaum et al (1992), Megiddo and Tamir (1993), Eduardo et al (2003), Cosares and Hochbaum (1994) are some among others. The techniques developed by these researchers are very much complicated and time-consuming. Recently, Adlakha and Kowalski (2013) have introduced an analytical algorithm for QTP which is based on finding absolute point (AP) in QTP by tracing graph for each quadratic cost function which is time-consuming and tedious and needs computer application for tracing graphs of each quadratic cost function.In the present paper, “A maximin zero suffix method” introduced by Sharma et al (2014) for solving assignment problems has been extended to solve QTP. To use this method, firstly estimated cost matrix of the QTP has to be obtained and then” A maximin zero suffix method” can be applied on the estimated cost matrix. This method is very simple, easy to apply and free from drawing graph of each quadratic cost function. An example of QTP from Adlakha and Kowalski (2013) has been considered to explain the “Maximin zero suffix method” for finding optimal solution.
There is no any efficient direct algorithm to solve QTP in the literature. However, QTP and its indirect solution techniques have been discussed by researchers including Hochbaum et al (1992), Megiddo and Tamir (1993), Eduardo et al (2003), Cosares and Hochbaum (1994) are some among others. The techniques developed by these researchers are very much complicated and time-consuming. Recently, Adlakha and Kowalski (2013) have introduced an analytical algorithm for QTP which is based on finding absolute point (AP) in QTP by tracing graph for each quadratic cost function which is time-consuming and tedious and needs computer application for tracing graphs of each quadratic cost function.In the present paper, “A maximin zero suffix method” introduced by Sharma et al (2014) for solving assignment problems has been extended to solve QTP. To use this method, firstly estimated cost matrix of the QTP has to be obtained and then” A maximin zero suffix method” can be applied on the estimated cost matrix. This method is very simple, easy to apply and free from drawing graph of each quadratic cost function. An example of QTP from Adlakha and Kowalski (2013) has been considered to explain the “Maximin zero suffix method” for finding optimal solution.
2. Estimated Cost Matrix
Firstly each quadratic cost is estimated to be constant cost. Then idea developed by Sharma et al (2014) is used to solve it. Per unit transporting cost of goods from 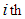 source to
source to 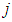
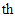 destination is
destination is 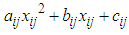 where
where 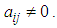 If
If 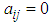 and
and 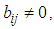 the problem is linear transportation problem (LTP). If
the problem is linear transportation problem (LTP). If 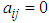 and
and 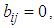 the problem is a classical transportation problem (CTP).The possible allocation to the
the problem is a classical transportation problem (CTP).The possible allocation to the 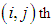 cell lies from 0 to min
cell lies from 0 to min 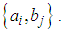 The maximum possible allocation to the
The maximum possible allocation to the 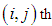 cell is
cell is 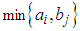 and the corresponding cost is
and the corresponding cost is 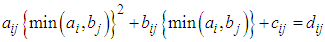 (say). The minimum possible allocation cost there is
(say). The minimum possible allocation cost there is 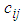 for the case of non allocation. Corresponding to the quadratic allocated cost matrix we have an
for the case of non allocation. Corresponding to the quadratic allocated cost matrix we have an 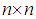 estimated cost
estimated cost 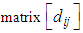 . Note that in the classical transportation problem at most cost is
. Note that in the classical transportation problem at most cost is 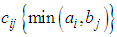 and at least cost is 0 in the case of non - allocation.
and at least cost is 0 in the case of non - allocation.
3. A Maximin Zero Suffix Method
Our goal is to find the minimum possible allocation cost which is possible when we allocate the lowest estimated cost cell.To obtain the minimum allocated cost, we search the least cost cell in the estimated cost matrix for possible allocation. After subtracting the lowest cost of each row from the corresponding row and then subtracting the lowest cost of each column from the corresponding column we get at least one zero in each row and each column in the transformed estimated cost matrix 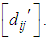 The lowest cost cells in each row and each column are detected by these zeros. On minimum cost distribution, zero cells (Lowest cost cells) should be assigned as far as possible satisfying the demand and supply conditions. Our aim is to assign zero cells one by one satisfying corresponding demand and supply conditions in such a manner that over all transporting cost becomes optimal one. The question is to which zero cells should be allocated firstly for getting an optimal transportation schedule.To overcome this critical situation we focus on two zero cells
The lowest cost cells in each row and each column are detected by these zeros. On minimum cost distribution, zero cells (Lowest cost cells) should be assigned as far as possible satisfying the demand and supply conditions. Our aim is to assign zero cells one by one satisfying corresponding demand and supply conditions in such a manner that over all transporting cost becomes optimal one. The question is to which zero cells should be allocated firstly for getting an optimal transportation schedule.To overcome this critical situation we focus on two zero cells 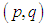 and
and 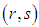 of the transformed estimated cost matrix. Let
of the transformed estimated cost matrix. Let 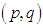 cell is assigned and
cell is assigned and 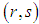 cell is not assigned. It means that
cell is not assigned. It means that 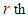 supplying source is not used for th demand destination. Then
supplying source is not used for th demand destination. Then 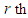 supply must be assigned to other demand. To assign
supply must be assigned to other demand. To assign  supply for minimum cost we select a cell in the
supply for minimum cost we select a cell in the 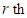 row whose cost is the next lowest cost in it’s row. Let
row whose cost is the next lowest cost in it’s row. Let 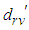 is the next minimum in the
is the next minimum in the 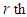 row. Then
row. Then 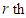 supply must be assigned to
supply must be assigned to 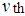 demand. So the excess cost in the absence of not assigning to
demand. So the excess cost in the absence of not assigning to 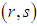 cell is
cell is 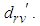 Also in the absence of not assigning to the
Also in the absence of not assigning to the 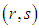 cell,
cell, 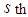 demand is not taken by the
demand is not taken by the 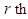 supply. To assign a value to the
supply. To assign a value to the 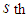 demand for minimum cost, we select a cell in the
demand for minimum cost, we select a cell in the 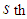 column whose cost is the next smallest in its column. Let
column whose cost is the next smallest in its column. Let 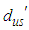 is the next minimum in the
is the next minimum in the 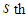 column. Then
column. Then 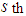 demand must be fulfilled by the
demand must be fulfilled by the 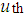 supply. So the excess cost in the absence of not assigning to the
supply. So the excess cost in the absence of not assigning to the 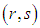 cell, the assignment cost may be increased at most by maximum of
cell, the assignment cost may be increased at most by maximum of 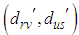 = max{lowest cost in its row, lowest cost in its column excluding itself} = suffix value of zero of the
= max{lowest cost in its row, lowest cost in its column excluding itself} = suffix value of zero of the 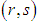 cell. Similarly, in case of not assigning to the
cell. Similarly, in case of not assigning to the 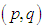 cell we may have to face excess cost which is equal to the suffix value of zero of the
cell we may have to face excess cost which is equal to the suffix value of zero of the 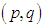 cell. Note that
cell. Note that 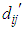 is the value of
is the value of 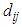 in the transformed estimated cost matrix. We conclude that to get minimum transportation cost it is better to assign that zero cell whose suffix value is the greatest one.The methodology of the paper is to block the path of exceeding cost above the optimal one in the process of assigning the zero cells. This is done by finding suffix value of all zeros of the transformed table and assignment is done to the cell having greatest suffix value. Then we have to delete the row/column of assigned cell to get the reduced table. The process is continued in the reduced table till all the demand and supply are exhausted.
in the transformed estimated cost matrix. We conclude that to get minimum transportation cost it is better to assign that zero cell whose suffix value is the greatest one.The methodology of the paper is to block the path of exceeding cost above the optimal one in the process of assigning the zero cells. This is done by finding suffix value of all zeros of the transformed table and assignment is done to the cell having greatest suffix value. Then we have to delete the row/column of assigned cell to get the reduced table. The process is continued in the reduced table till all the demand and supply are exhausted.
4. Algorithm
The algorithm of maximin zero suffix method for finding an optimal solution of quadratic transportation problem (QTP) consists of the following steps: Step 1. Construct the estimated cost matrix 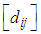 where
where 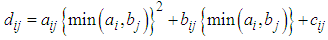 Step 2. Subtract the least element of each row from all the elements of the corresponding row of the estimated cost matrixStep 3. Subtract the least element of each column from all the elements of the corresponding column obtained in step 2 to get the transformed estimated cost matrix
Step 2. Subtract the least element of each row from all the elements of the corresponding row of the estimated cost matrixStep 3. Subtract the least element of each column from all the elements of the corresponding column obtained in step 2 to get the transformed estimated cost matrix 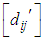 Step 4. Find the suffix value of each zero cell
Step 4. Find the suffix value of each zero cell 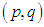 using the following formula. Suffix value of the cell
using the following formula. Suffix value of the cell 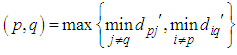 Step 5. Assign the cell having the greatest suffix value and delete the exhausted row/column to get the reduced estimated cost matrix Step 6. In the reduced table update
Step 5. Assign the cell having the greatest suffix value and delete the exhausted row/column to get the reduced estimated cost matrix Step 6. In the reduced table update 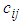 for those cells whose
for those cells whose 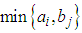 is reduced by
is reduced by 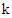 as
as 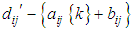 Step 7. Repeat steps 2 to 6 till all the demands and supplies are exhausted.
Step 7. Repeat steps 2 to 6 till all the demands and supplies are exhausted.
5. A Numerical Example
Let us consider the cost matrix  for the QTP given in Adlakha and Kowalski (2013).
for the QTP given in Adlakha and Kowalski (2013).Table 1.
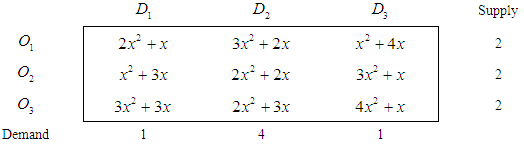 |
| |
|
Step 1. Estimated cost matrix of the given QTP isTable 2.
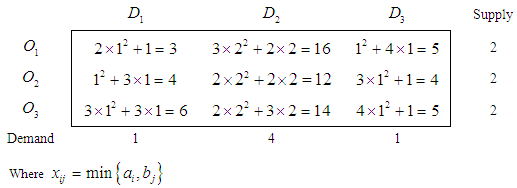 |
| |
|
Step 2. Subtracting the row minimum from the respective row in table 2, we getTable 3.
 |
| |
|
Step 3. Subtracting Column minimum from the respective column in table 3, we getTable 4.
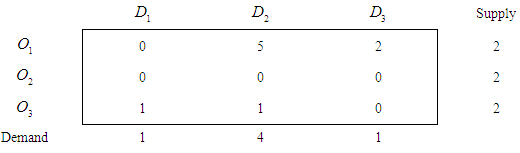 |
| |
|
Step 4. Suffix Value of each zero in table 4 is shown in table 5 along with the allocated amount to be shipped. Table 5.
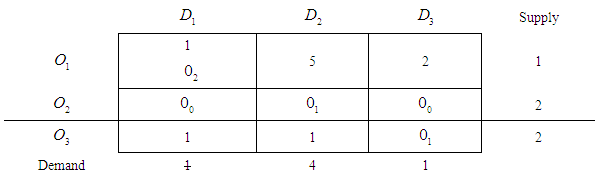 |
| |
|
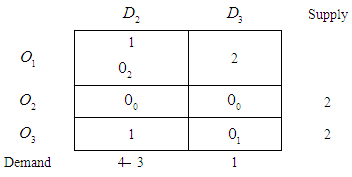
Step 5. Reduced estimated cost matrix with updated 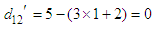 has been obtained and shown in table 6 along with suffix value of zeros and allocated amount to be shipped
has been obtained and shown in table 6 along with suffix value of zeros and allocated amount to be shippedTable 6.
 |
| |
|
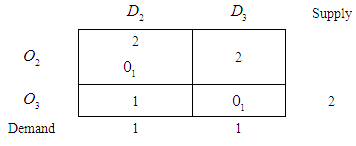
Now repeating steps 2 to 6 we getTable 7.
 |
| |
|
Table 8.
 |
| |
|
Finally an optimal transportation table is as follows: 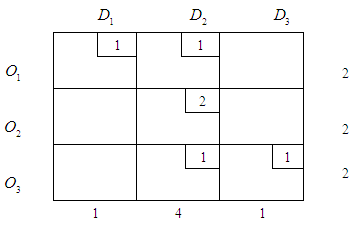 The minimum cost for the given QTP can be obtained as
The minimum cost for the given QTP can be obtained as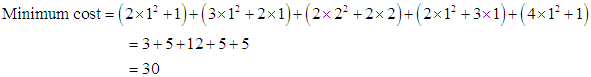 It would be recalled that the total minimum transportation cost for the above QTP obtained by Adlakha and Kowalski (2013) is also 30.
It would be recalled that the total minimum transportation cost for the above QTP obtained by Adlakha and Kowalski (2013) is also 30.
6. Optimality Criteria and Convergence of the Algorithm
Since we have used the method of minimizing the excess transporting cost corresponding to a cell by assigning the lowest cost cell in each row and each column, there is no chance that the cost obtained according to this process is higher than the optimal cost.As the number of rows and the number of columns are finite and at each iteration one row or one column is deleted, the algorithm will terminate in a finite number of steps. The number of iterations will be at most m + n and at least max (m, n).
7. Concluding Remarks
A maximin zero suffix method has been introduced to solve the quadratic transportation problem (QTP). The proposed method is better than all existing methods in the literature for solving QTP because it is free from any huge algebraic computation and drawing of graphs of quadratic cost functions to search absolute point. The algorithm of the proposed method has been given and the application of the proposed method has been explained by a numerical example. The proposed method is very simple, easy to understand and apply for any practitioners who have not much knowledge of Mathematics and therefore useful for managerial decisions. The proposed maximin zero suffix method for solving QTP can be extended to the polynomial transportation problem (PTP) in which the cost coefficients are higher than second degree polynomials.The future research on the proposed method is to apply the method for solving real-world problem. For using this method to solve real-world problems a computer program must be developed because the real-world problems consist of several sources and destinations which is difficult to handle manually. Since the proposed method is easy to apply and understand, it can be easily applied to solve real-world problems.
ACKNOWLEDGEMENTS
The authors would like to thank the Editor-In-Chief and the referee for careful reading and for their constructive comments and suggestions which improved the quality of the paper.
References
| [1] | Adlakha, V. and Kowalski (1999): An Alternative Solution Algorithm for Certain Transportation Problems, International Journal of Mathematical Education in Science and Technology, 30(5), 719 – 728. |
| [2] | Adlakha, V. and Kowalski (2013): On the Quadratic Transportation Problem, Open Journal of Optimization, 2, 89 - 94. |
| [3] | Arsham, H. and Khan, A.B. (1989): A Simplex Type Algorithm for General Transportation Problems – An Alternative to Stepping Stone, Journal of Operational Research Society, 40(6), 581 – 590. |
| [4] | Charnes, A. and Cooper, W.W. (1954): The Stepping Stone Method for explaining Linear Programming Calculations in Transportation Problems, Management Science, 1(1), 49 – 69. |
| [5] | Cosares, S. and Hochbaum, D.S. (1994): Strongly Polynomial Algorithms for the Quadratic Ttransportation Problems with a fixed number of sources, Mathematics of Operations Research, 19(1), 94 – 111. |
| [6] | Dantzig, G.B. (1963): Linear Programming and Extensions, Princeton university press, Princeton, NJ. |
| [7] | Eduardo, M.B., Francisco, S.J.D. and Real, J.R. (2003): Adaptive Productivity Theory to the Quadratic Cost function-An Application to the Spanish Electric Sector, Journal of Productivity Analysis, 20(2), 233 – 249. |
| [8] | Hitchcock, F.L. (1941): The Distribution of a Product from Several Sources to Numerous Localities, Journal of Mathematics and Physics, 20, 224 – 230. |
| [9] | Hochbaum, D.S. Shamir, R. and Shanthikumar, J.G. (1992): A Polynomial Algorithm for an Integer Quadratic Non-Separable Transportation Problem, Mathematical Programming, 55, no 1-3, 359 – 371. |
| [10] | Ji, P. and Chu, K.F. (2002): A Dual Matrix Approach to the Transportation Problem, Asia Pacific Journal of Operations Research, 19 (1), 35 - 45. |
| [11] | Korukoglu, S. and Balli, S. (2011): An Improved Vogel’s Approximation Method for the Transportation Problem, Mathematical and Computational Applications, 16 (2), 370 - 381. |
| [12] | Megiddo, N. and Tamir, A. (1993): Linear Time Algorithms for Some Separable Quadratic Programming Problems, Operations research letters, 13(4), 203 – 211. |
| [13] | Sharma, S., Shanker, R. and Shanker, R. (2013): A Modified Zero Suffix Method for finding Optimal Solution for Transportation Problems, European Journal of Scientific Research, 104(4), 673 – 676. |
| [14] | Sharma, S., Shanker, R. and Shanker, R. (2014): A Maximin Zero Suffix Method for Solving Assignment Problems, European Journal of Scientific Research, 126(2), 206-212. |
| [15] | Shih, W. (1987): Modified Stepping Stone Method as a Teaching aid for Capacitated Transportation Problems, Decision Sciences, 18, 662 - 676. |
| [16] | Sudhakar, V.J., Arunsankar, N. and Karpagam, T. (2012): A new approach for finding an Optimal Solution for Transportation Problems, European Journal of Scientific Research, 68(2), 254 – 257. |


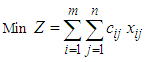
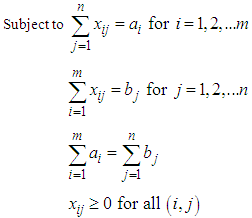 where
where 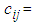 Unit transportation cost from
Unit transportation cost from 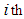 source to
source to 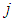 th destination
th destination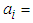 Amount of goods available at th source.
Amount of goods available at th source.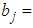 Amount of goods required at th destination
Amount of goods required at th destination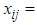 Amount of goods transported from th source to
Amount of goods transported from th source to 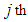 destination.
destination.
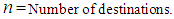 CTP, being a well structured problem, has been studied extensively in the literature. It was Hitchcock (1941) who firstly developed the basic transportation problem and suggested constructive method of solution. Later on, Dantzig (1963) formulated the CTP as an LPP and provided the solution. A number of researchers have worked to find suitable methods of solving CTP using different assumptions including Charnes and Cooper (1954), Shih (1987), Arsham and Khan (1989), Adlakha and Kowalski (1999), Ji and Chu (2002), Korukoglu and Balli (2011), Sudhakar et al (2012), are some among others. Recently Sharma et al (2013) have introduced an easy and interesting method named, “A modified zero suffix method” for finding optimal solution for CTP.In the real life situation, per unit transportation cost of goods does not remain always constant. Generally, it decreases with the increase in the volume of transported goods but not always. Sometimes, it has also been seen that it increases with the increase in the volume of the transported goods due to highway congestion (restriction of over loading). This idea leads to a new dimension of the CTP and generally it has been observed that per unit cost
CTP, being a well structured problem, has been studied extensively in the literature. It was Hitchcock (1941) who firstly developed the basic transportation problem and suggested constructive method of solution. Later on, Dantzig (1963) formulated the CTP as an LPP and provided the solution. A number of researchers have worked to find suitable methods of solving CTP using different assumptions including Charnes and Cooper (1954), Shih (1987), Arsham and Khan (1989), Adlakha and Kowalski (1999), Ji and Chu (2002), Korukoglu and Balli (2011), Sudhakar et al (2012), are some among others. Recently Sharma et al (2013) have introduced an easy and interesting method named, “A modified zero suffix method” for finding optimal solution for CTP.In the real life situation, per unit transportation cost of goods does not remain always constant. Generally, it decreases with the increase in the volume of transported goods but not always. Sometimes, it has also been seen that it increases with the increase in the volume of the transported goods due to highway congestion (restriction of over loading). This idea leads to a new dimension of the CTP and generally it has been observed that per unit cost 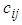 is a function of the amount shipped
is a function of the amount shipped 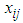 . If the per unit transportation cost
. If the per unit transportation cost 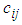 in CTP is a quadratic function
in CTP is a quadratic function 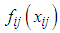 of
of 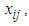 then CTP is termed as the quadratic transportation problem (QTP). In QTP, the cost coefficients are quadratic functions, and in CTP the cost coefficients are constants.Mathematically, the quadratic transportation problem (QTP) is defined as
then CTP is termed as the quadratic transportation problem (QTP). In QTP, the cost coefficients are quadratic functions, and in CTP the cost coefficients are constants.Mathematically, the quadratic transportation problem (QTP) is defined as 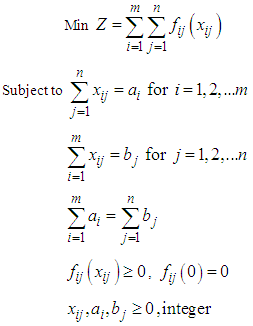 There is no any efficient direct algorithm to solve QTP in the literature. However, QTP and its indirect solution techniques have been discussed by researchers including Hochbaum et al (1992), Megiddo and Tamir (1993), Eduardo et al (2003), Cosares and Hochbaum (1994) are some among others. The techniques developed by these researchers are very much complicated and time-consuming. Recently, Adlakha and Kowalski (2013) have introduced an analytical algorithm for QTP which is based on finding absolute point (AP) in QTP by tracing graph for each quadratic cost function which is time-consuming and tedious and needs computer application for tracing graphs of each quadratic cost function.In the present paper, “A maximin zero suffix method” introduced by Sharma et al (2014) for solving assignment problems has been extended to solve QTP. To use this method, firstly estimated cost matrix of the QTP has to be obtained and then” A maximin zero suffix method” can be applied on the estimated cost matrix. This method is very simple, easy to apply and free from drawing graph of each quadratic cost function. An example of QTP from Adlakha and Kowalski (2013) has been considered to explain the “Maximin zero suffix method” for finding optimal solution.
There is no any efficient direct algorithm to solve QTP in the literature. However, QTP and its indirect solution techniques have been discussed by researchers including Hochbaum et al (1992), Megiddo and Tamir (1993), Eduardo et al (2003), Cosares and Hochbaum (1994) are some among others. The techniques developed by these researchers are very much complicated and time-consuming. Recently, Adlakha and Kowalski (2013) have introduced an analytical algorithm for QTP which is based on finding absolute point (AP) in QTP by tracing graph for each quadratic cost function which is time-consuming and tedious and needs computer application for tracing graphs of each quadratic cost function.In the present paper, “A maximin zero suffix method” introduced by Sharma et al (2014) for solving assignment problems has been extended to solve QTP. To use this method, firstly estimated cost matrix of the QTP has to be obtained and then” A maximin zero suffix method” can be applied on the estimated cost matrix. This method is very simple, easy to apply and free from drawing graph of each quadratic cost function. An example of QTP from Adlakha and Kowalski (2013) has been considered to explain the “Maximin zero suffix method” for finding optimal solution. 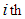 source to
source to 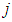
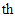 destination is
destination is 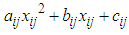 where
where 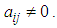 If
If 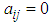 and
and 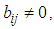 the problem is linear transportation problem (LTP). If
the problem is linear transportation problem (LTP). If 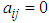 and
and 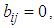 the problem is a classical transportation problem (CTP).The possible allocation to the
the problem is a classical transportation problem (CTP).The possible allocation to the 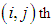 cell lies from 0 to min
cell lies from 0 to min 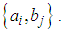 The maximum possible allocation to the
The maximum possible allocation to the 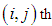 cell is
cell is 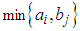 and the corresponding cost is
and the corresponding cost is 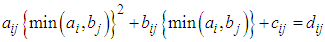 (say). The minimum possible allocation cost there is
(say). The minimum possible allocation cost there is 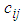 for the case of non allocation. Corresponding to the quadratic allocated cost matrix we have an
for the case of non allocation. Corresponding to the quadratic allocated cost matrix we have an 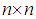 estimated cost
estimated cost 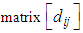 . Note that in the classical transportation problem at most cost is
. Note that in the classical transportation problem at most cost is 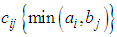 and at least cost is 0 in the case of non - allocation.
and at least cost is 0 in the case of non - allocation.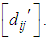 The lowest cost cells in each row and each column are detected by these zeros. On minimum cost distribution, zero cells (Lowest cost cells) should be assigned as far as possible satisfying the demand and supply conditions. Our aim is to assign zero cells one by one satisfying corresponding demand and supply conditions in such a manner that over all transporting cost becomes optimal one. The question is to which zero cells should be allocated firstly for getting an optimal transportation schedule.To overcome this critical situation we focus on two zero cells
The lowest cost cells in each row and each column are detected by these zeros. On minimum cost distribution, zero cells (Lowest cost cells) should be assigned as far as possible satisfying the demand and supply conditions. Our aim is to assign zero cells one by one satisfying corresponding demand and supply conditions in such a manner that over all transporting cost becomes optimal one. The question is to which zero cells should be allocated firstly for getting an optimal transportation schedule.To overcome this critical situation we focus on two zero cells 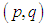 and
and 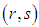 of the transformed estimated cost matrix. Let
of the transformed estimated cost matrix. Let 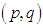 cell is assigned and
cell is assigned and 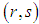 cell is not assigned. It means that
cell is not assigned. It means that 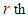 supplying source is not used for th demand destination. Then
supplying source is not used for th demand destination. Then 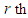 supply must be assigned to other demand. To assign
supply must be assigned to other demand. To assign  supply for minimum cost we select a cell in the
supply for minimum cost we select a cell in the 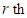 row whose cost is the next lowest cost in it’s row. Let
row whose cost is the next lowest cost in it’s row. Let 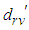 is the next minimum in the
is the next minimum in the 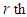 row. Then
row. Then 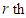 supply must be assigned to
supply must be assigned to 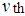 demand. So the excess cost in the absence of not assigning to
demand. So the excess cost in the absence of not assigning to 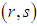 cell is
cell is 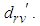 Also in the absence of not assigning to the
Also in the absence of not assigning to the 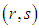 cell,
cell, 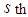 demand is not taken by the
demand is not taken by the 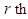 supply. To assign a value to the
supply. To assign a value to the 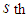 demand for minimum cost, we select a cell in the
demand for minimum cost, we select a cell in the 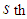 column whose cost is the next smallest in its column. Let
column whose cost is the next smallest in its column. Let 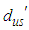 is the next minimum in the
is the next minimum in the 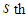 column. Then
column. Then 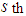 demand must be fulfilled by the
demand must be fulfilled by the 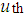 supply. So the excess cost in the absence of not assigning to the
supply. So the excess cost in the absence of not assigning to the 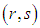 cell, the assignment cost may be increased at most by maximum of
cell, the assignment cost may be increased at most by maximum of 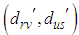 = max{lowest cost in its row, lowest cost in its column excluding itself} = suffix value of zero of the
= max{lowest cost in its row, lowest cost in its column excluding itself} = suffix value of zero of the 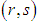 cell. Similarly, in case of not assigning to the
cell. Similarly, in case of not assigning to the 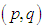 cell we may have to face excess cost which is equal to the suffix value of zero of the
cell we may have to face excess cost which is equal to the suffix value of zero of the 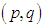 cell. Note that
cell. Note that 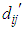 is the value of
is the value of 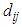 in the transformed estimated cost matrix. We conclude that to get minimum transportation cost it is better to assign that zero cell whose suffix value is the greatest one.The methodology of the paper is to block the path of exceeding cost above the optimal one in the process of assigning the zero cells. This is done by finding suffix value of all zeros of the transformed table and assignment is done to the cell having greatest suffix value. Then we have to delete the row/column of assigned cell to get the reduced table. The process is continued in the reduced table till all the demand and supply are exhausted.
in the transformed estimated cost matrix. We conclude that to get minimum transportation cost it is better to assign that zero cell whose suffix value is the greatest one.The methodology of the paper is to block the path of exceeding cost above the optimal one in the process of assigning the zero cells. This is done by finding suffix value of all zeros of the transformed table and assignment is done to the cell having greatest suffix value. Then we have to delete the row/column of assigned cell to get the reduced table. The process is continued in the reduced table till all the demand and supply are exhausted.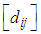 where
where 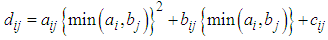 Step 2. Subtract the least element of each row from all the elements of the corresponding row of the estimated cost matrixStep 3. Subtract the least element of each column from all the elements of the corresponding column obtained in step 2 to get the transformed estimated cost matrix
Step 2. Subtract the least element of each row from all the elements of the corresponding row of the estimated cost matrixStep 3. Subtract the least element of each column from all the elements of the corresponding column obtained in step 2 to get the transformed estimated cost matrix 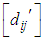 Step 4. Find the suffix value of each zero cell
Step 4. Find the suffix value of each zero cell 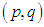 using the following formula. Suffix value of the cell
using the following formula. Suffix value of the cell 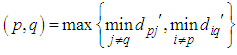 Step 5. Assign the cell having the greatest suffix value and delete the exhausted row/column to get the reduced estimated cost matrix Step 6. In the reduced table update
Step 5. Assign the cell having the greatest suffix value and delete the exhausted row/column to get the reduced estimated cost matrix Step 6. In the reduced table update 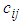 for those cells whose
for those cells whose 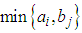 is reduced by
is reduced by 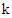 as
as 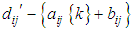 Step 7. Repeat steps 2 to 6 till all the demands and supplies are exhausted.
Step 7. Repeat steps 2 to 6 till all the demands and supplies are exhausted.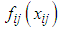 for the QTP given in Adlakha and Kowalski (2013).
for the QTP given in Adlakha and Kowalski (2013).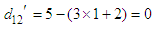 has been obtained and shown in table 6 along with suffix value of zeros and allocated amount to be shipped
has been obtained and shown in table 6 along with suffix value of zeros and allocated amount to be shipped The minimum cost for the given QTP can be obtained as
The minimum cost for the given QTP can be obtained as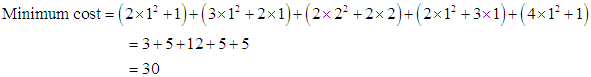 It would be recalled that the total minimum transportation cost for the above QTP obtained by Adlakha and Kowalski (2013) is also 30.
It would be recalled that the total minimum transportation cost for the above QTP obtained by Adlakha and Kowalski (2013) is also 30. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML