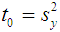-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2016; 6(2): 33-39
doi:10.5923/j.ajor.20160602.01

Use of Correlation Coefficient and Quartiles of Auxiliary Variable for Improved Estimation of Population Variance
Subhash Kumar Yadav1, S. S. Mishra1, Alok Kumar Shukla2
1Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India
2Department of Statistics, D.A.V College, Kanpur, U.P., India
Correspondence to: S. S. Mishra, Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The present paper deals with the estimation of population variance using correlation coefficient and quartiles of an auxiliary variable under simple random sampling scheme. Up to the first order of the approximation, the bias and the mean square error of the proposed estimator have been obtained. The optimum value of the characterizing scalar kappa has been obtained and for this optimum value of kappa, the minimum mean square error of the proposed estimator has also been obtained up to the first order of approximation. A comparison of the proposed estimator has been made with existing estimators of population variance under simple random sampling scheme. An empirical study is also carried out to justify the theoretical findings. An improvement over existing estimators has been shown in the sense of having lesser mean square error.
Keywords: Ratio estimator, Quartiles, Bias, Mean squared error, Efficiency
Cite this paper: Subhash Kumar Yadav, S. S. Mishra, Alok Kumar Shukla, Use of Correlation Coefficient and Quartiles of Auxiliary Variable for Improved Estimation of Population Variance, American Journal of Operational Research, Vol. 6 No. 2, 2016, pp. 33-39. doi: 10.5923/j.ajor.20160602.01.
Article Outline
1. Introduction
- In survey sampling, auxiliary information is used for enhancing the efficiency of the estimate of the parameters of the population for the characteristic under study. Auxiliary information is supplied by the auxiliary variable which is highly positively or negatively correlated with the main variable under study. Ratio type estimators are used when the variables x and y are positively correlated and the line of regression of y on x passes through origin, while the product type estimators are used when x and y are negatively correlated to each other otherwise regression estimators are used. In the present study, we are dealing with only the positive correlation.Let
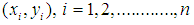 be the n pair of observations for the auxiliary and study variables, respectively from the population of size N using simple random sampling without replacement. Let
be the n pair of observations for the auxiliary and study variables, respectively from the population of size N using simple random sampling without replacement. Let 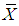 and
and 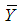 be the population means of auxiliary and study variables respectively and
be the population means of auxiliary and study variables respectively and 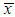 and
and 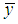 be the respective sample means.Following are the notations which have been used in this manuscript and are already being discussed by Subramani and Kumarpandiyan (2015) as:
be the respective sample means.Following are the notations which have been used in this manuscript and are already being discussed by Subramani and Kumarpandiyan (2015) as: 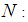 Size of the population
Size of the population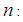 Size of the sample
Size of the sample 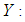 Study variable
Study variable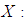 Auxiliary variable
Auxiliary variable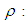 Correlation coefficient between
Correlation coefficient between 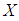 and
and 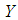
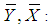 Population means
Population means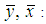 Sample means
Sample means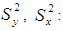 Population variances
Population variances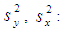 Sample variances
Sample variances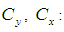 Coefficient of variations
Coefficient of variations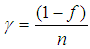
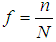
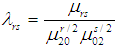
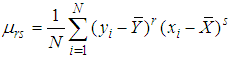
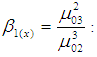 Skewness of the auxiliary variable
Skewness of the auxiliary variable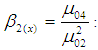 Kurtosis of the auxiliary variable
Kurtosis of the auxiliary variable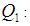 First quartile of the auxiliary variable
First quartile of the auxiliary variable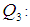 Third quartile of the auxiliary variable
Third quartile of the auxiliary variable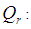 Inter quartile range of the auxiliary variable
Inter quartile range of the auxiliary variable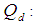 Semi quartile range of the auxiliary variable
Semi quartile range of the auxiliary variable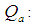 Semi quartile average of the auxiliary variable
Semi quartile average of the auxiliary variable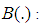 Bias of the estimator
Bias of the estimator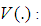 Variance of the estimator
Variance of the estimator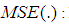 Mean squared error of the estimator
Mean squared error of the estimator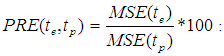 Percentage relative efficiency of the estimator
Percentage relative efficiency of the estimator 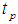 over
over 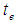 The appropriate estimator of the population variance is the sample variance defined as
The appropriate estimator of the population variance is the sample variance defined as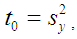 | (1.1) |
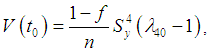 | (1.2) |
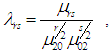
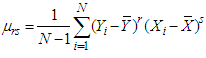 and
and 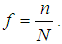 Isaki (1983) utilizing the auxiliary information, proposed the following classical ratio estimator for the population variance as
Isaki (1983) utilizing the auxiliary information, proposed the following classical ratio estimator for the population variance as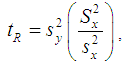 | (1.3) |
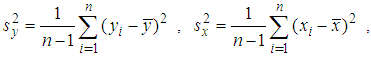
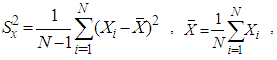
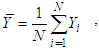
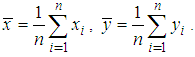 , The expressions for the Bias and Mean Square Error (MSE) of the estimator in (1.3) up to the first order of approximation respectively are as
, The expressions for the Bias and Mean Square Error (MSE) of the estimator in (1.3) up to the first order of approximation respectively are as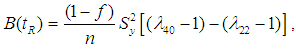 | (1.4) |
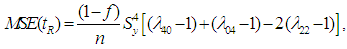 | (1.5) |
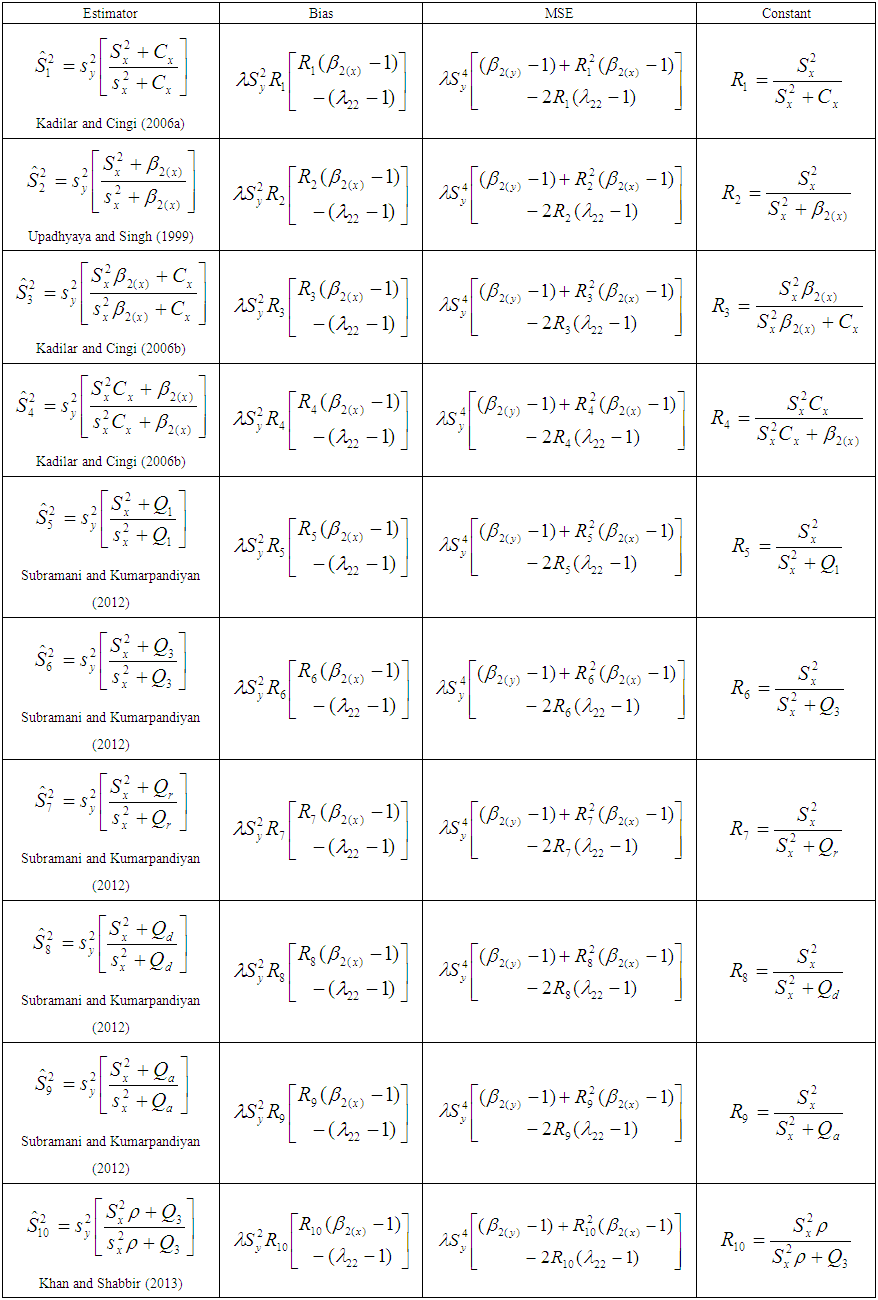 | Table 1. Bias, MSE and Constants of different estimators |
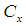 is the coefficient of variation of auxiliary variable,
is the coefficient of variation of auxiliary variable, 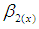 is the coefficient of kurtosis,
is the coefficient of kurtosis, 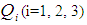 are the quartiles of the auxiliary variable.
are the quartiles of the auxiliary variable. 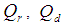 and
and 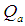 are the functions of quartiles defined by,
are the functions of quartiles defined by,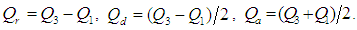 Thus, in general the mean square errors of the estimators given in above table may be written as,
Thus, in general the mean square errors of the estimators given in above table may be written as,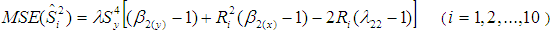 | (1.6) |
2. Proposed Estimator
- Motivated by Prasad (1989) and Khan and Shabbir (2013), we propose an efficient ratio estimator of population variance as
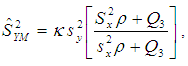 | (2.1) |
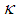 is a suitable constant to be determined such that the mean square error of
is a suitable constant to be determined such that the mean square error of 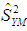 is minimum.In order to study the large sample properties of the proposed estimator,
is minimum.In order to study the large sample properties of the proposed estimator, 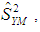 we define
we define 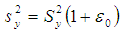 and
and 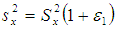 with
with 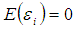 for
for 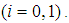 In case of simple random sampling without replacement, ignoring finite population correction term, the following expectations could be obtained either directly or by the method due to Kendall and Stuart (1977) as
In case of simple random sampling without replacement, ignoring finite population correction term, the following expectations could be obtained either directly or by the method due to Kendall and Stuart (1977) as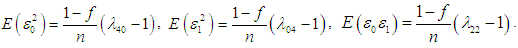 Expressing
Expressing 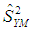 in terms of
in terms of 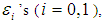 we have
we have 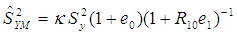 After simplifying and retaining terms up to the first order of approximation, we have:
After simplifying and retaining terms up to the first order of approximation, we have: 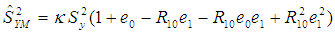 Subtracting
Subtracting 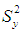 on both the sides, we obtain,
on both the sides, we obtain,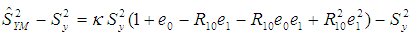 | (2.2) |
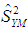 as:
as: 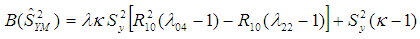 | (2.3) |
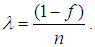 The mean squared error of the proposed estimator
The mean squared error of the proposed estimator 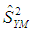 is obtained by squaring both sides of (2.2), simplifying and taking expectation on both sides, up to the first order of approximation as,
is obtained by squaring both sides of (2.2), simplifying and taking expectation on both sides, up to the first order of approximation as,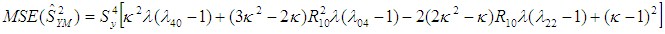 | (2.4) |
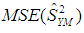 is minimum for,
is minimum for, 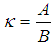 | (2.5) |
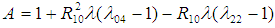 and
and 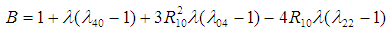 The minimum MSE of the estimator
The minimum MSE of the estimator 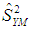 for this optimum value of
for this optimum value of 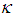 is:
is: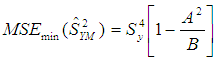 | (2.6) |
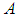 and
and 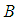 can be obtained from the previous surveys or the experience gathered in due course of time, for instance, vide Murthy (1967), Reddy (1973, 1974), Srivenkataramana & Tracy (1980), Singh & Vishwakarma (2008), Singh & Kumar (2008) and Singh & Karpe (2010). If the unknown parameters in
can be obtained from the previous surveys or the experience gathered in due course of time, for instance, vide Murthy (1967), Reddy (1973, 1974), Srivenkataramana & Tracy (1980), Singh & Vishwakarma (2008), Singh & Kumar (2008) and Singh & Karpe (2010). If the unknown parameters in 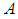 and
and 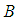 are replaced by their estimates, then we obtain the same minimum mean squared error as in (2.6).
are replaced by their estimates, then we obtain the same minimum mean squared error as in (2.6).3. Efficiency Comparison
- From (2.6) and (1.2), we have:
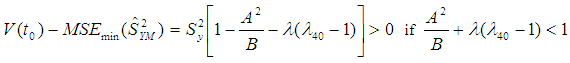 | (3.1) |
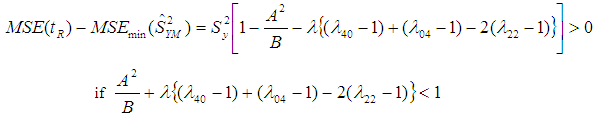 | (3.2) |
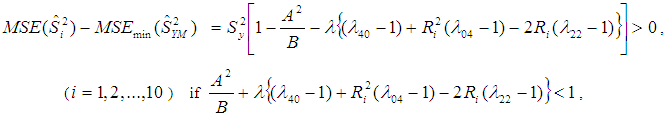 | (3.3) |
4. Numerical Illustration
- To justify the theoretical findings of different estimators, we have considered the following real populations.Population-1: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Total amount (tons) of recyclable-waste collection in Italy in 2002.
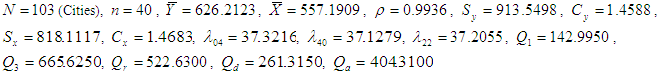 Population-2: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Number of inhabitants in 2003.
Population-2: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Number of inhabitants in 2003.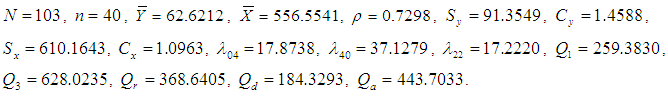 Population-3: Murthy (1967) Y: Output for 80 factories in a region.X: Fixed capital.
Population-3: Murthy (1967) Y: Output for 80 factories in a region.X: Fixed capital.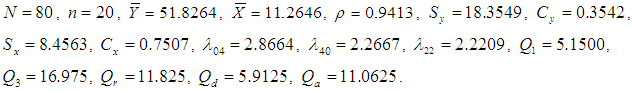 Population-4: Singh and Chaudhary (1986)
Population-4: Singh and Chaudhary (1986) 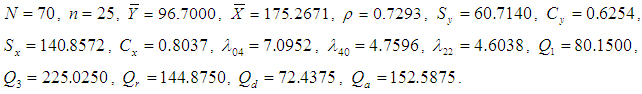
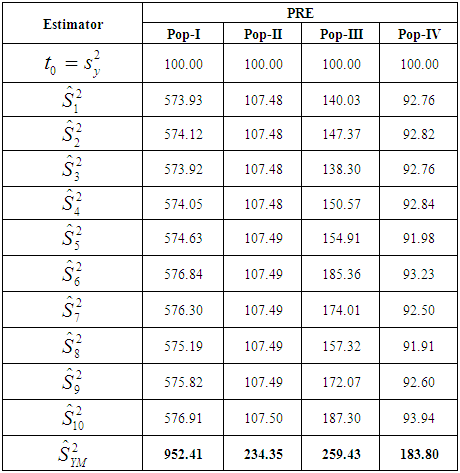
5. Observation and Conclusions
- Table-1 shows the Bias, MSE and Constants for previously existing estimators given by different researchers. Proposed estimator which has been subjected to comparisons with previous estimators nothing but is a ratio estimator. In this paper, we have been able to develop more efficient estimator whose bias is significantly far much less as compared to previous estimators as evidently presented in table-2. Similarly, MSE is also far much less as compared to previous estimators given in the table-2. Moreover, table-3 shows that relative efficiency is comparatively much higher. Thus, we can finally conclude with passing remarks that from theoretical discussions in section-3 and the results in table-2 and 3, we infer that the proposed estimator is much better than the previously existing estimators of population mean in simple random sampling scheme, therefore proposed estimator should be preferred for the estimation of population variance.
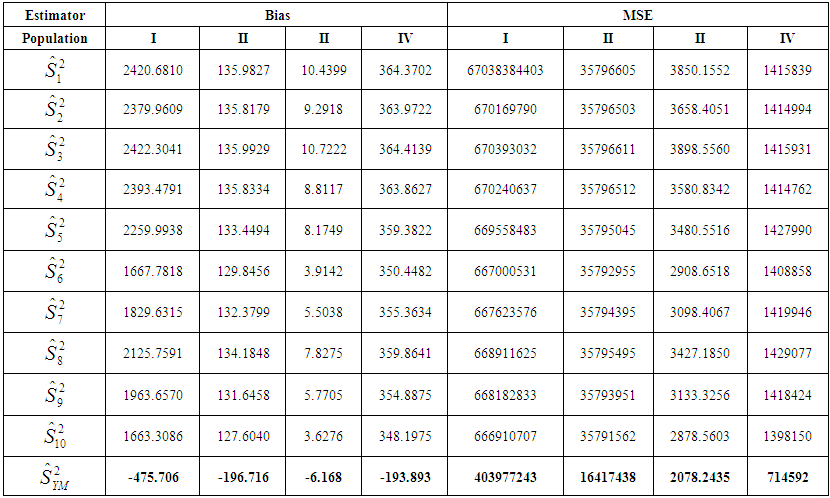 | Table 2. Bias and Mean square error of different estimators |
|
ACKNOWLEDGMENTS
- The authors are very much thankful to the editor of American Journal of Operational Research and the anonymous referees for critically examining the manuscript and giving the valuable suggestions to improve the manuscript in present form.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML