| [1] | Covert, R.P. and Philip, G.C. (1973) An EOQ model for Weibull deteriorating items. AIIE Transactions, 5, 323-326. http://dx.doi.org/10.1080/05695557308974918. |
| [2] | Buzacott, J.A. (1975) Economic order quantity model for deteriorating items under inflation. Operation Research Quarterly, 26, 553-558. http://dx.doi.org/10.1057/jors.1975.113. |
| [3] | Mcdonald, J.J. (1979) Inventory replenishment policy for computational solutions. Journal of Operation Research Society, 30, 933-936. http://dx.doi.org/10.2307/3009548. |
| [4] | Deb, M. and Chaudhuri, K.S. (1987) A note on the Heuristic inventory model for the replenishment of trended inventories considering shortages. Journal of Operation Research Society, 38, 459-463. |
| [5] | Datta, T.K. and Pal, A.K. (1991) Effect of inflation and time value of money on an inventory model with linear time dependent demand rate and shortages. European Journal of Operation Research, 52, 326-333.http://dx.doi.org/10.1016/0377-2217(91) 90167-T. |
| [6] | Mandal, B. and Pal, A.K. (1998) An order level inventory system with ramp-type demand rate for deteriorating items. Journal of Interdisciplinary Mathematics, 1, 49-66. http://dx.doi.org/10.1080/09720502.1998.10700243. |
| [7] | Chang, H.J. and Dye, C.Y. (1999) An EOQ model for deteriorating items with time varying demand and partial backlogging. Journal of Operation Research Society, 50, 1176-1182. http://dx.doi.org/10.2307/3010088. |
| [8] | Wu, K.S. and Ouyang, L.Y. (2000) A replenishment policy for deteriorating items with ramp-type demand rate. Proceeding of the National Science Council, Republic of China, 24(4), 279-286. |
| [9] | Wu, K.S. (2001) An EOQ model for Weibull deteriorating items with ramp-type demand rate and partial backlogging. Production Planning and Control, 12, 787-793. http://dx.doi.org/10.1080/09537280110051819. |
| [10] | Teng, J.T., Chang, H.J. Dye, C.Y. and Hung, C.H. (2002) An optimal replenishment policy for deteriorating items with ramp-type demand and partial backlogging. Operation Research Letters, 30, 387-393. http://dx.doi.org/ 10.1016/S0167-6377(02)00150-5. |
| [11] | Manna, S.K. and Choudhuri, K.S. (2003) An EOQ model with ramp-type demand rate, time dependent deterioration rate, unit production cost and shortages. International Journal of Systems Science, 34(3), 237-243. |
| [12] | Giri, B.C., Jalan, A.K. and Chaudhuri, K.S. (2003) Economic order quantity model for Weibull deteriorating items with ramp-type demand and shortage. International Journal of System Science, 34, 237-243.http://dx.doi.org/10.1080/0020772131000158500. |
| [13] | Jaggi, C.K., Aggarwal, K.K. and Goel, S.K. (2006) Optimal order policy for deteriorating items under inflation induced Demand. International Journal of Production Economic, 103, 707-714. http://dx.doi.org/10.1016/j.ijpe.2006.01.004. |
| [14] | Dye, C.Y., Chang, H.J. and Teng, J.T. (2006) A deteriorating inventory model with time varying demand and shortage dependent partial backlogging. European Journal of Operation Research, 172, 417-429.http://dx.doi.org/10.1016/j.ejor.2004.10.025. |
| [15] | Deng, P.S., Lin, RH-J., Chu, P. (2007) A note on inventory models for deteriorating items with ramp-type demand rate. European Journal of Operation Research, 178, 112-120. |
| [16] | Panda, S., Senapati, S. and Basu, M. (2008) Optimal replenishment policy for perishable seasonal products in a season with ramp-type time dependent demand. Computers and Industrial Engineering, 54, 301-314. |
| [17] | Kun-Shan, W., Liang-Yuh, O. and Chih-Te, Y. (2008) A retailer’s optimal ordering policy for deteriorating items with ramp-type demand under stock-dependent consumption rate. Information and Management Science, 19(2), 245-262. |
| [18] | Chung, C.J. and Wee, H.M. (2008) An integrated production inventory model for deteriorating items with pricing policy considering imperfect production, inspection planning and warranty period and stock level dependent demand. International Journal of System Science, 39, 823-837. http://dx.doi.org/10.1080/00207720801902598. |
| [19] | Skouri, K., Konstantaras, I., Papachristos, S. and Ganas, I. (2009) Inventory model for Weibull deteriorating items with ramp-type demand rate and partial backlogging. European Journal of Operation Research, 192, 79-92. http://dx.doi.org/10.1016/j.ejor.2007.09.003. |
| [20] | Cardenas-Barron, L.E. (2009) Economic production quantity model with rework process at a single-stage manufacturing system with planned backorders. Computer and Industrial Engineering, 57, 1105-1113.http://dx.doi.org/10.1016/j.cie.2009.04.020. |
| [21] | Jain, S. and Kumar, M. (2010) proposed an EOQ model for three parameter weibull deteriorating items with ramp-type demand rate and shortages. Yugoslav Journal of Operation Research, 20(2), 249-259. |
| [22] | Sana, S.S. (2010) Demand influenced by enterprises initiative –a multi item EOQ model for deteriorating ameliorating items. Mathematical and Computer Modeling, 52, 284-302. http://dx.doi.org/ 10.1016/j.mcm.2010.02.045. |
| [23] | Sarkar, B., Sana, S. and Chaudhuri, K. (2010) Optimal reliability, production lot size and safety stock. An economic manufacturing quantity model. International Journal of Management Science and Engineering Management, 5, 192-202. |
| [24] | Sana, S.S. (2010) Optimal selling price and lot size inventory model with time varying deterioration and partial backlogging. Applied Mathematics and Computation, 217, 185-194. |
| [25] | Chang, C.T. (2011) developed an inventory model for weibull deteriorating items with ramp-type demand rate and partial backlogging. Tamsui Oxford Journal of Information and Mathematical Sciences, 27(1), 61-66. |
| [26] | Wee, H.M., Lee, M.C., Yu, J.C.P. and Wang, C.E. (2011) An optimal replenishment policy for a deteriorating green product, lifecycle costing analysis. International Journal of Production Economics, 133, 603-611.http://dx.doi.org/10.1016/j.ijpe.2011.05.001. |
| [27] | Cardenas-Barron, L.E. (2011) An economic production quantity (EPQ) with shortage derived algebraically. International Journal of Production Economics, 70, 289-292. http://dx.doi.org/10.1016/S0925-5273(00)00068-2. |
| [28] | Sarkar, B. and Moon, I. (2011) An equivalent production quantity (EPQ) model with inflation in an imperfect production system. Applied Mathematics and Computation, 217, 6159-6167.http://dx.doi.org/10.1016/j.amc.2010.12.098. |
| [29] | Sett, B.K., Sarkar, B. and Goswami, A. (2012) A two warehouse inventory model with increasing demand and time varying deterioration. Scientia Iranica. E, 19, 1969-1977. http://dx.doi.org/10.1016/j.scient.2012.10.040. |
| [30] | Ahmad, M.A., Al-khana, T.A., Benkherouf, L. (2013) Inventory models with ramp-type demand rate, partial backlogging and general deterioration rate. Applied Mathematics and Computation, 219, 4288-4307. |
| [31] | Cardenas-Barron, L.E., Sarkar, B. and Trevino Garza, G. (2013) An improved solution to the replenishment policy for the EMQ model with rework and multiple shipments. Applied Mathematical Modeling, 37, 5549-5554.http://dx.doi.org/10.1016/j.apm.2012.10.017. |
| [32] | Sarkar, B. and Majumder, A. (2013) Integrated vendor buyer supply chain model with vendors setup cost reduction. Applied Mathematics and Computation, 224, 362-371. http://dx.doi.org/10.1016/j.amc.2013.08.072. |
| [33] | Cardenas-Barron, L.E., Sarkar, B. and Trevindo-Garza, G. (2013) Easy and improved algorithms to joint determination of the replenishment lot size and number of shipments for an EPQ model with rework. Mathematical and Computational Algorithms, 18, 132-138. |
| [34] | Karamakar, B. and Choudhury, K.B. (2014) proposed an inventory model for deteriorating items with ramp-type demand rate, partial backlogging and time varying holding cost. Yugoslav Journal of Operation Research, 24(2), 249-266. |
| [35] | Sarkar, B., Saren, S. and Cardenas-Barron, L.E. (2014) An inventory model with trade credit policy and variable deterioration for fixed lifetime products. Annals of Operation Research, http://dx.doi.org/10.1007/s10479-014-1745-9. |
| [36] | Sarkar, B., Mandal, P. and Sarkar, S. (2014) An EMQ model with price and time dependent demand under the effect of reliability and inflation. Applied Mathematics and Computation, 231, 414-421.http://dx.doi.org/10.1016/j.amc.2014.01.004. |
| [37] | Sarkar, B., Chaudhuri, K. and Moon, I. (2015) developed a distribution free continuous review inventory model with service level constraint for the reduction of manufacturing set up cost. Journal of Manufacturing System, 34, 74-82. http://dx.doi.org/10.1016/j.msy.2014.11.003. |
| [38] | Kumar, V., Sharma, A. and Gupta, C.B. (2015) formulated a two warehouse partial backlogging inventory model for deteriorating items with ramp-type demand. Innovative Systems Design and Engineering, 6(2), 86-97. |


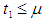 with respect to the change in deterioration parameter
with respect to the change in deterioration parameter 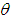 and inflation parameter
and inflation parameter 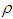 , the tables 3 and 4 show that the variation of total profit when
, the tables 3 and 4 show that the variation of total profit when 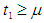 with respect to the change in deterioration parameter
with respect to the change in deterioration parameter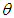 and inflation parameter
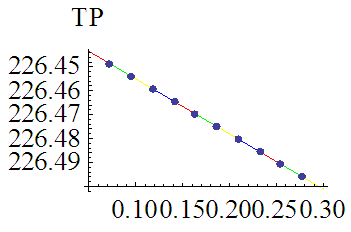
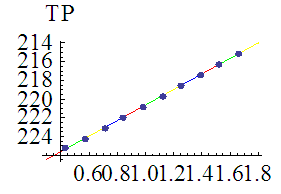
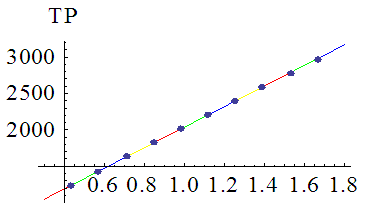
and inflation parameter 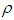 . The figures 1 and 2 are correspond to the developed model in two cases
. The figures 1 and 2 are correspond to the developed model in two cases 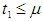 and
and 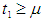 . The figures 3 and 4 show that the variation of total profit when
. The figures 3 and 4 show that the variation of total profit when 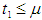 with respect to the change in deterioration parameter
with respect to the change in deterioration parameter 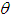 and inflation parameter
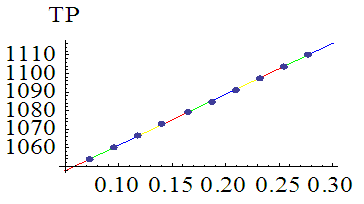
and inflation parameter 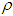 and the figures 5 and 6 show that the variation of total profit when
and the figures 5 and 6 show that the variation of total profit when 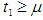 with respect to the change in deterioration parameter
with respect to the change in deterioration parameter 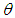 and inflation parameter
and inflation parameter 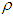 .
.
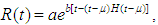 where a is the initial demand rate and b a constant governing exponential demand rate and
where a is the initial demand rate and b a constant governing exponential demand rate and  is the Heaviside unit step function of time defined by
is the Heaviside unit step function of time defined by 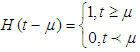 2. The selling rate is influenced by the demand rate and on hand inventory stock by,
2. The selling rate is influenced by the demand rate and on hand inventory stock by, 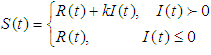 3. Where, k is a positive constant.4.
3. Where, k is a positive constant.4. 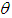 is the probabilistic deterioration rate.5.
is the probabilistic deterioration rate.5. 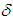 is the backlogging parameter.6.
is the backlogging parameter.6. 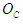 is the ordering cost per order.7.
is the ordering cost per order.7. 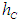 is the holding cost per unit8.
is the holding cost per unit8. 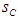 is the shortage cost.9.
is the shortage cost.9. 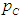 is the purchase cost per unit.10.
is the purchase cost per unit.10. 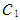 is the lost sell cost per unit.11.
is the lost sell cost per unit.11. 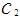 is the selling price per unit.12. r is the discount rate represent the time value of money.13. i is the inflation rate per unit time. 14.
is the selling price per unit.12. r is the discount rate represent the time value of money.13. i is the inflation rate per unit time. 14. 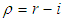 is the discount rate minus inflation rate.15.
is the discount rate minus inflation rate.15. 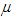 is the parameter of ramp-type demand rate.16.
is the parameter of ramp-type demand rate.16. 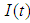 is the inventory level at any time in [0,T].17.
is the inventory level at any time in [0,T].17. 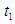 is the time of zero inventory level.18. T is the length of each ordering cycle.19. Q is the order quantity per cycle.20. The replenishment rate is infinite.21. Shortages are allowed and partially backlogged.22. The lead time is zero.23.
is the time of zero inventory level.18. T is the length of each ordering cycle.19. Q is the order quantity per cycle.20. The replenishment rate is infinite.21. Shortages are allowed and partially backlogged.22. The lead time is zero.23. 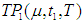 is the total profit per unit time for model I.24.
is the total profit per unit time for model I.24. 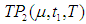 is the total profit per unit time for model II.
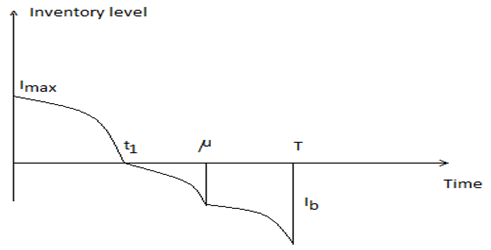
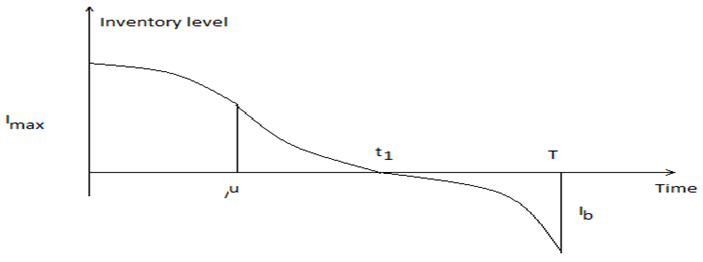
is the total profit per unit time for model II.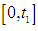 the inventory level decreases due to both demand and deterioration and becomes zero at
the inventory level decreases due to both demand and deterioration and becomes zero at 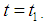 The shortage starts at
The shortage starts at 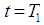 and shortage interval is the end of current order cycle. During the shortage interval
and shortage interval is the end of current order cycle. During the shortage interval 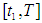 shortages are allowed and partially backlogged. The unsatisfied demand is backlogged at rate of
shortages are allowed and partially backlogged. The unsatisfied demand is backlogged at rate of 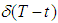 , where t is the waiting time and the positive constant
, where t is the waiting time and the positive constant 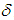 is the backlogging parameter.The instantaneous inventory level at any time t in
is the backlogging parameter.The instantaneous inventory level at any time t in 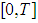 is governed by the following differential equations
is governed by the following differential equations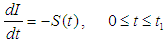
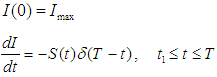
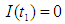 The solution of these equations is affected by the selling rate. Now we discuss the following two cases
The solution of these equations is affected by the selling rate. Now we discuss the following two cases 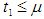 and
and 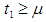 Case I When
Case I When 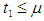 then in the interval
then in the interval 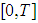 the selling rate
the selling rate 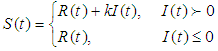 is defined as
is defined as 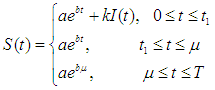 Using
Using  in equations 1 and 2
in equations 1 and 2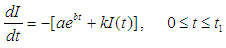
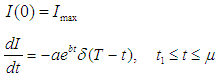
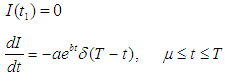
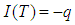 The equation (3) can also be written as
The equation (3) can also be written as 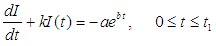 For the solution of equation (3) the integrating factor is
For the solution of equation (3) the integrating factor is 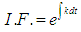 and the solution of equation (3) is
and the solution of equation (3) is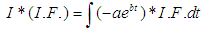 The solution of equation (3) is
The solution of equation (3) is 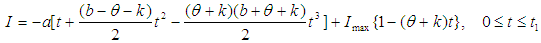
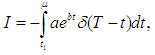 The solution of equation (4) is
The solution of equation (4) is 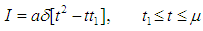
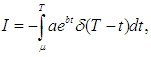 The solution of equation (5) is
The solution of equation (5) is 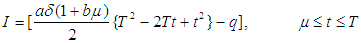
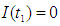 and from the equation (6) we obtain
and from the equation (6) we obtain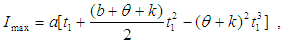
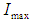 in the equation (6) we obtain the solution of equation (3)
in the equation (6) we obtain the solution of equation (3)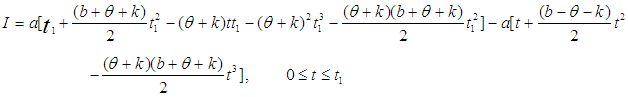
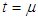 then from the equations (7) and (8)
then from the equations (7) and (8)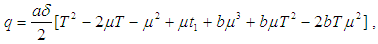
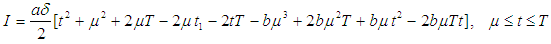
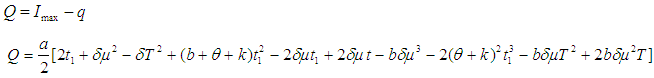
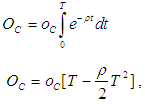
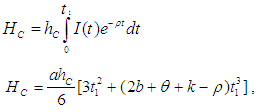
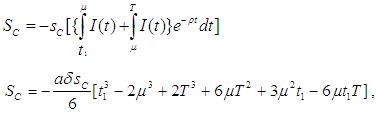
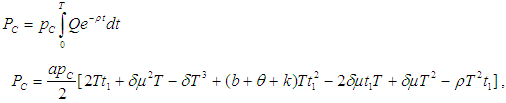
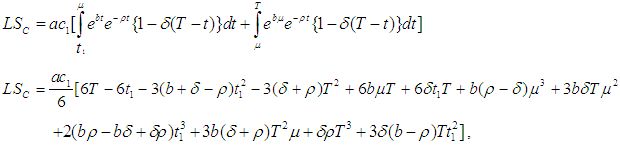
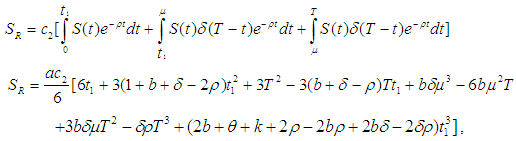
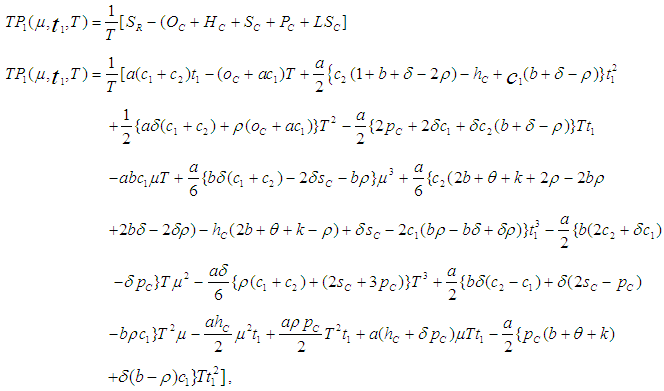
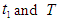 for which the total profit
for which the total profit 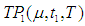 is maximum.The necessary condition for
is maximum.The necessary condition for 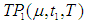 to be maximum is that
to be maximum is that 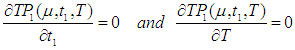 and solving these equations we find the optimum values of
and solving these equations we find the optimum values of 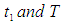 say for which profit is maximum and the sufficient condition is
say for which profit is maximum and the sufficient condition is 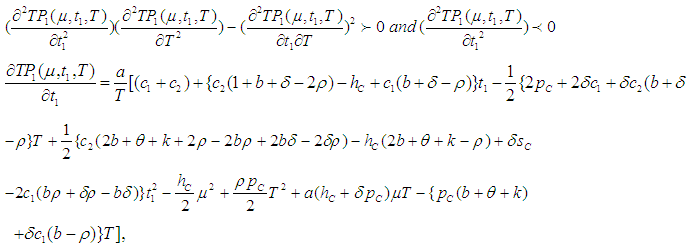
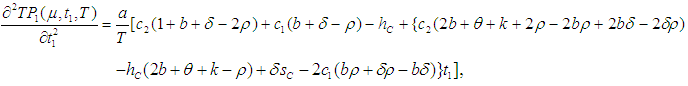
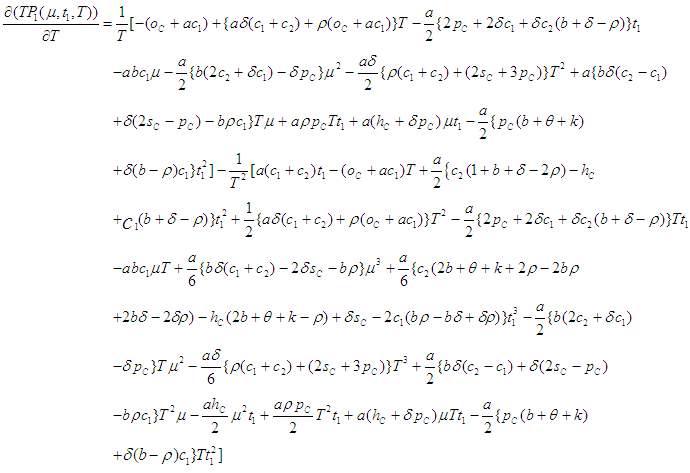
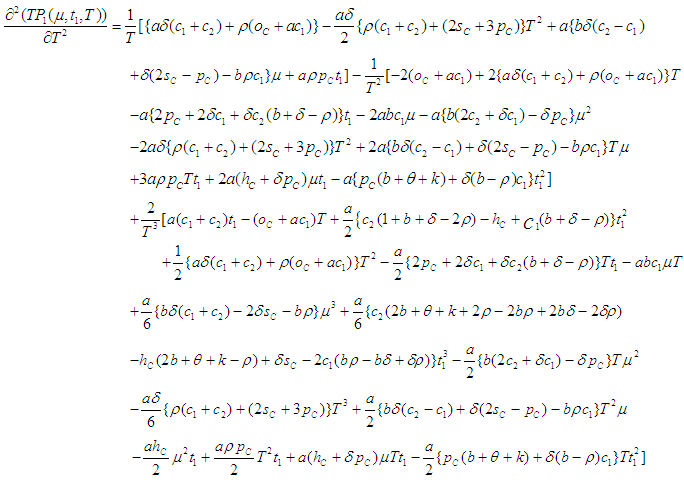
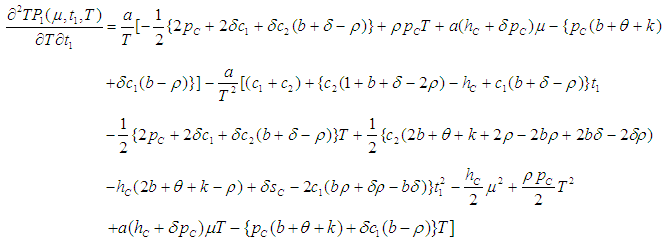
 then in the interval
then in the interval 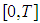 the selling rate
the selling rate 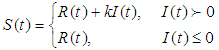 is defined as
is defined as 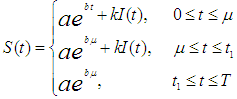 Then the instantaneous inventory level at any time
Then the instantaneous inventory level at any time 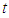 in
in 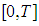 are governed by the following differential equations
are governed by the following differential equations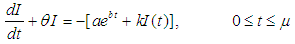
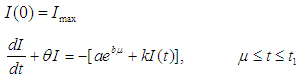
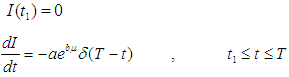
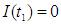 The solution of the equation (21) is
The solution of the equation (21) is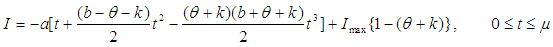
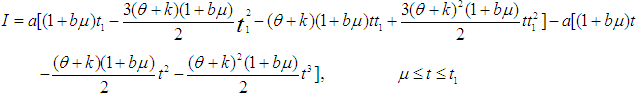
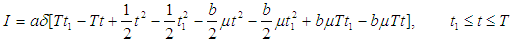
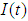 , putting
, putting 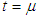 in the equation (24)
in the equation (24) 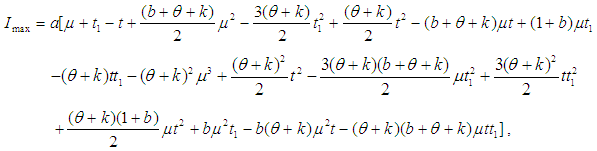
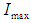 in the equation (24), the solution of the equation (21) is
in the equation (24), the solution of the equation (21) is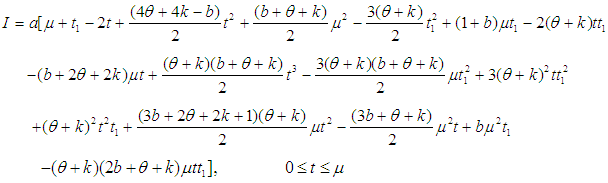
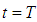 in the equation (26)
in the equation (26)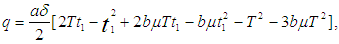
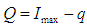
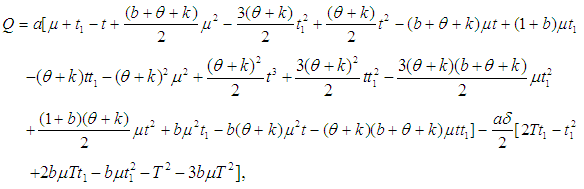
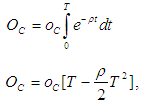
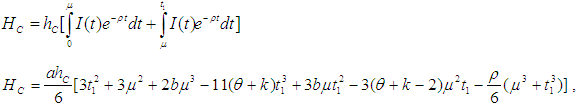
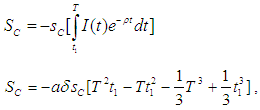
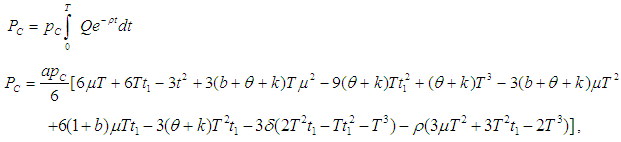
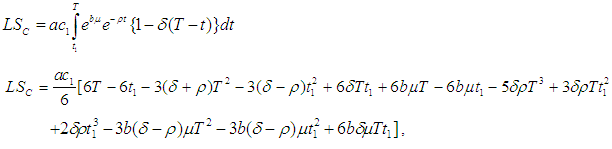
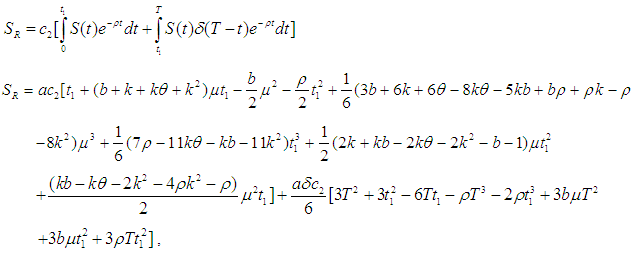
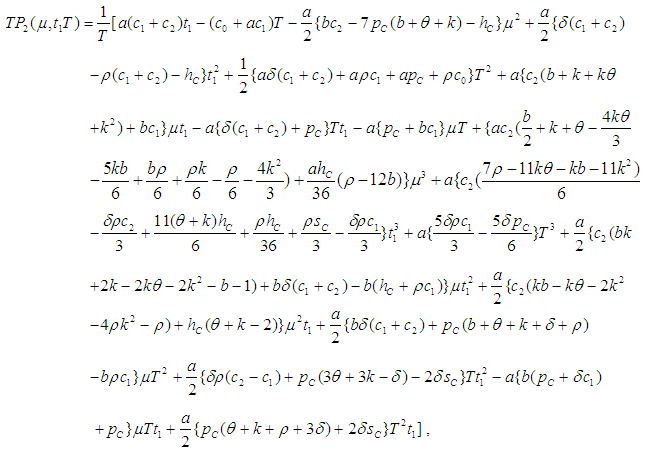
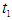 for which the total profit
for which the total profit 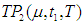 is maximum.The necessary condition for
is maximum.The necessary condition for 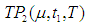 to be maximum is that
to be maximum is that 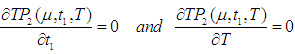 and solving these equations we find the optimum values of
and solving these equations we find the optimum values of 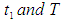 say for which profit is maximum and the sufficient condition is
say for which profit is maximum and the sufficient condition is 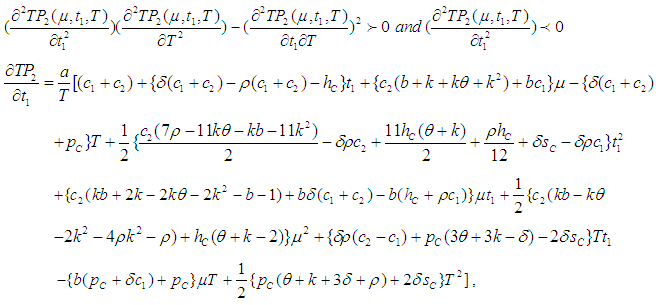
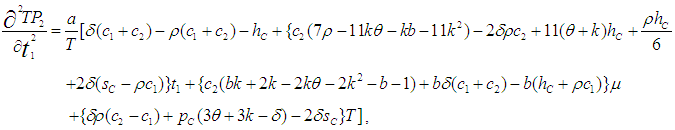
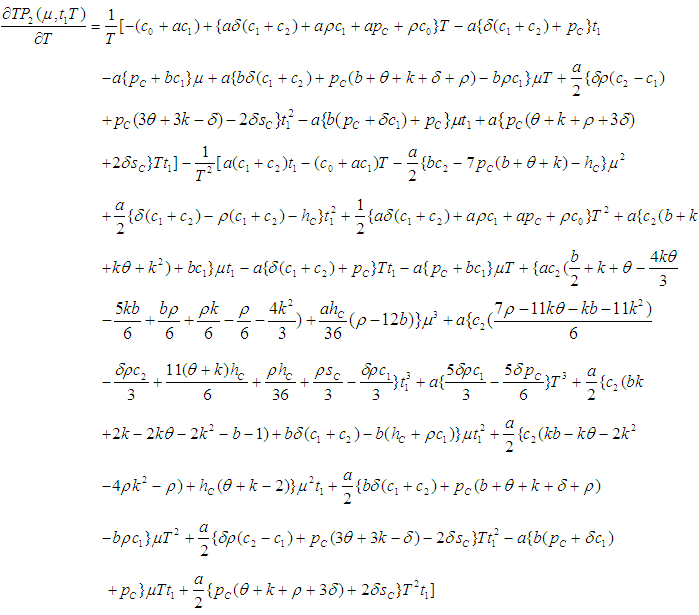

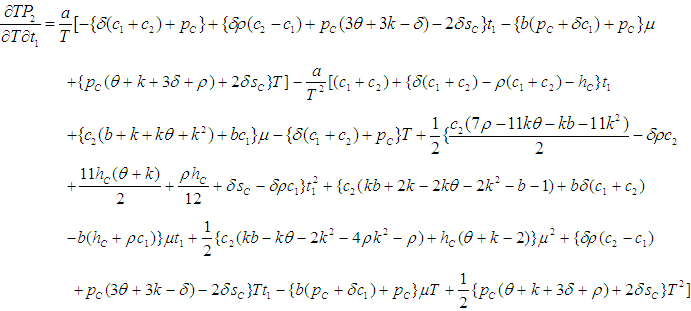
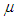
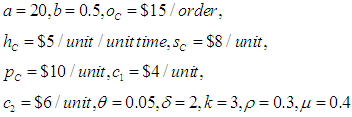 Numerical example 1- when
Numerical example 1- when 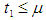 then solving the equations
then solving the equations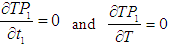 we find the optimum value of
we find the optimum value of 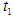 and
and 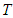 for different values of
for different values of 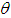 and
and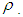
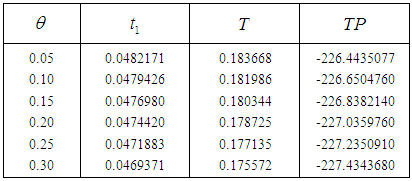
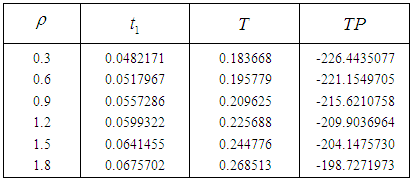
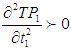 so the total profit is minimum. As we increase the deterioration parameter
so the total profit is minimum. As we increase the deterioration parameter 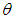 then the total profit decreases.
then the total profit decreases.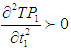 so the total profit is minimum. As we increase the inflation parameter
so the total profit is minimum. As we increase the inflation parameter 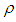 then the total profit increases.Numerical example 2- when
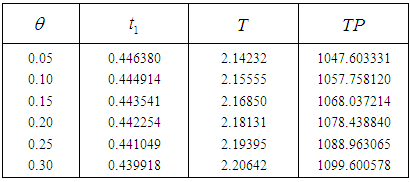
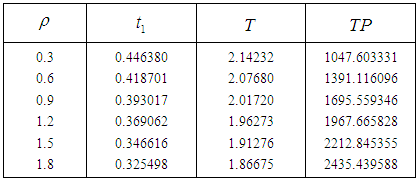
then the total profit increases.Numerical example 2- when 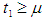 then solving the equations
then solving the equations 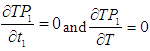 we find the optimum value of
we find the optimum value of 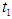 and
and 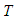 for different values of
for different values of 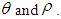
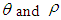 are more sensitive in case of
are more sensitive in case of 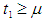 in comparison of
in comparison of 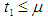 because in the case I shortage interval is greater than the shortage interval in case II and so the total profit is minimum in case I and the total profit is maximum in case II.
because in the case I shortage interval is greater than the shortage interval in case II and so the total profit is minimum in case I and the total profit is maximum in case II.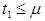 and
and 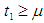 . In case I from the tables 1 and 2 we see that as we increase the parameters
. In case I from the tables 1 and 2 we see that as we increase the parameters 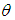 and
and 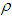 then the total profit is minimum. In case II from the tables 3 and 4 we see that as we increase the parameters
then the total profit is minimum. In case II from the tables 3 and 4 we see that as we increase the parameters 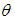 and
and 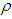 then the total profit is maximum. Thus when
then the total profit is maximum. Thus when 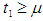 then the deterioration parameter
then the deterioration parameter 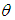 and the inflation parameter
and the inflation parameter 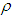 become more sensitive in comparison of deterioration parameter
become more sensitive in comparison of deterioration parameter 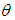 and inflation parameter
and inflation parameter 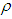 in case of
in case of 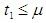 because in the case I the shortage interval is greater than the shortage interval in case II. Further this model can be generalized by considering the fuzzy type demand rate.
because in the case I the shortage interval is greater than the shortage interval in case II. Further this model can be generalized by considering the fuzzy type demand rate. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML