Subhash Kumar Yadav1, Sheela Misra2, S. S. Mishra1
1Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India
2Department of Statistics, University of Lucknow, Lucknow, U.P., India
Correspondence to: S. S. Mishra, Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Population variance is one of the important measures of dispersion. For example one is interested in knowing the estimate of variance of a particular crop, blood pressure, temperature etc. This paper deals with the estimation of population variance using auxiliary information under simple random sampling scheme. In the present paper, we have proposed an improved estimator through well known kappa technique using Yadav et al (2014) paper. The large sample properties of the estimator have been studied up to the first order of approximation that is its bias and mean square error have been obtained up to the first order of approximation. The optimum value of the characterizing scalar kappa has been obtained and for this optimum value of the kappa the minimum mean squared error has been obtained. A comparison has been made with the existing estimators of population variance using secondary data. An improvement of the proposed estimator has been shown over all existing mentioned estimators as it has lesser mean square error as compared to other estimators.
Keywords:
Ratio estimator, Quartiles, Bias, Mean squared error, Efficiency
Cite this paper: Subhash Kumar Yadav, Sheela Misra, S. S. Mishra, Efficient Estimator for Population Variance Using Auxiliary Variable, American Journal of Operational Research, Vol. 6 No. 1, 2016, pp. 9-15. doi: 10.5923/j.ajor.20160601.02.
1. Introduction
In the theory of survey sampling, the auxiliary information plays paramount role in developing and searching improved estimators of population parameters of the study variable. The auxiliary information is used at both the stages of designing and estimation. Here we have used this information at estimation stage only. The auxiliary variable (X) and the main variable (Y) under study are highly closely related with each other. When there is a close positive association between the study variable and the auxiliary variable and the line of regression of the study variable Y on the auxiliary variable X passes through origin, then the ratio type estimator is used for improvement over the parameters of the population under consideration. On the other hand the product type estimators are used for improved estimation of parameters when the auxiliary variable x and the study variable y have negative correlation between them. While the regression type estimators are used for the improved estimation of population parameters, when the line of regression does not pass through the origin.Let the population under investigation is finite and it consists of N distinct and identifiable units. Let 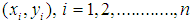 be a random sample of size n from above bivariate population (X, Y) of size N using a SRSWOR scheme. Let
be a random sample of size n from above bivariate population (X, Y) of size N using a SRSWOR scheme. Let 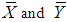 respectively are the population means of the auxiliary and the study variables, and let
respectively are the population means of the auxiliary and the study variables, and let 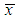 and
and 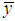 are the corresponding sample means which are unbiased estimators of population means
are the corresponding sample means which are unbiased estimators of population means 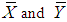 respectively. Let
respectively. Let 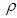 denote the correlation coefficient between the variables X and Y and
denote the correlation coefficient between the variables X and Y and 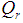 is the inter-quartile range of the auxiliary variable X. In this manuscript, we have proposed an improved ratio type estimator of population variance of study variable by suitably using the correlation coefficient
is the inter-quartile range of the auxiliary variable X. In this manuscript, we have proposed an improved ratio type estimator of population variance of study variable by suitably using the correlation coefficient 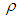 between the two variables and
between the two variables and 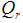 , inter-quartile range of the auxiliary variable X. Further we assume that a reliable estimate of the correlation coefficient
, inter-quartile range of the auxiliary variable X. Further we assume that a reliable estimate of the correlation coefficient 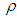 is available in advance from pilot surveys etc.
is available in advance from pilot surveys etc.
2. Variance Estimators in Literature
The sample variance is the most appropriate estimator of population variance and is given by: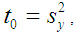 | (2.1) |
This estimator of population variance is unbiased, and it has the variance up to the first degree of approximation as: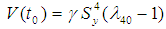 | (2.2) |
Isaki (1983) proposed the following ratio estimator of population variance using auxiliary information as: 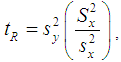 | (2.3) |
where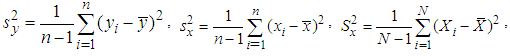
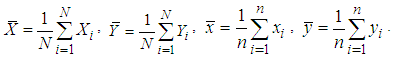 The first order of approximations for the Bias and Mean Square Error (MSE) respectively are given by
The first order of approximations for the Bias and Mean Square Error (MSE) respectively are given by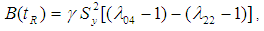 | (2.4) |
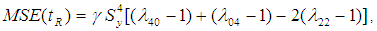 | (2.5) |
where 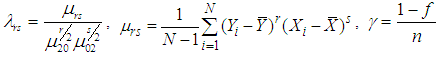 and
and 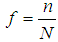 .Several authors proposed different estimators by utilizing auxiliary information in different forms. They used it in the form of different parameters of auxiliary variable for estimating the population variance of the main variable under study. Some of them from the literature are as follows, Upadhyaya and Singh (1999) utilized coefficient of kurtosis
.Several authors proposed different estimators by utilizing auxiliary information in different forms. They used it in the form of different parameters of auxiliary variable for estimating the population variance of the main variable under study. Some of them from the literature are as follows, Upadhyaya and Singh (1999) utilized coefficient of kurtosis  of auxiliary variable and proposed the following estimator of population variance as,
of auxiliary variable and proposed the following estimator of population variance as,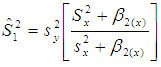 | (2.6) |
The bias and Mean Squared Error of above estimator up to the first order of approximations respectively are, 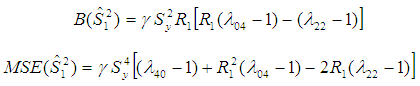 | (2.7) |
Where, 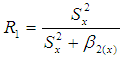 Kadilar and Cingi (2006) proposed the following estimators using different parameters of auxiliary information as,
Kadilar and Cingi (2006) proposed the following estimators using different parameters of auxiliary information as,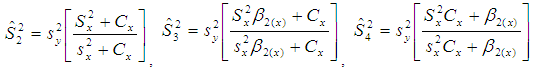 The bias and Mean Squared Error of above estimators up to the first order of approximations respectively are,
The bias and Mean Squared Error of above estimators up to the first order of approximations respectively are, 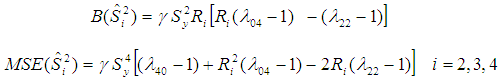 | (2.8) |
Where, 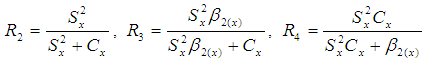 Subramani and Kumarpandiyan (2012), utilizing various population parameters of auxiliary variable proposed the following estimators of population variance as,
Subramani and Kumarpandiyan (2012), utilizing various population parameters of auxiliary variable proposed the following estimators of population variance as,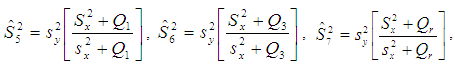
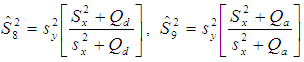 The expressions for the bias and Mean Squared Error of above estimators up to the first order of approximations respectively are,
The expressions for the bias and Mean Squared Error of above estimators up to the first order of approximations respectively are, 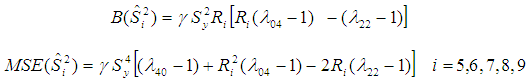 | (2.9) |
Where, 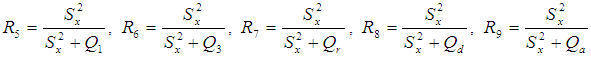 Where
Where 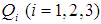 are the quartiles, the three points dividing the whole distribution into four equal parts. Further the functions of quartiles are, the inter quartile range,
are the quartiles, the three points dividing the whole distribution into four equal parts. Further the functions of quartiles are, the inter quartile range, 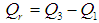 , the semi-quartile range
, the semi-quartile range 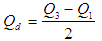 and the quartile average
and the quartile average 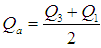 . Khan and Shabbir (2013) proposed the following estimator using correlation coefficient and the third quartile of the auxiliary variable as,
. Khan and Shabbir (2013) proposed the following estimator using correlation coefficient and the third quartile of the auxiliary variable as,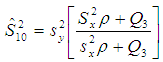 The expressions for the bias and Mean Squared Error of the estimator up to the first order of approximations respectively are,
The expressions for the bias and Mean Squared Error of the estimator up to the first order of approximations respectively are, 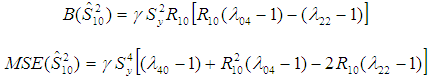 | (2.10) |
Where, 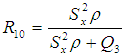 Yadav et al. (2014), utilizing the correlation coefficient of the inter-quartile range of auxiliary variable proposed the following estimator as,
Yadav et al. (2014), utilizing the correlation coefficient of the inter-quartile range of auxiliary variable proposed the following estimator as,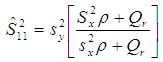 The bias and Mean Squared Error of the above estimator up to the first order of approximations respectively are,
The bias and Mean Squared Error of the above estimator up to the first order of approximations respectively are,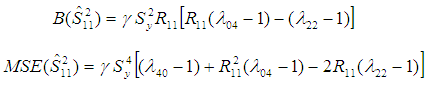 | (2.11) |
Where, 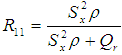 .
.
3. Proposed Estimator
Here, an improved ratio estimator of population variance is being suggested in the light of estimators proposed by Yadav et al. (2014) and Prasad (1989) as, 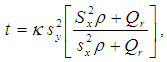 | (3.1) |
where 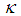 is a characterizing scalar to be determined such that the MSE of the proposed estimator t is minimized. To obtain the bias and Mean squared error of the proposed estimator, we wish to define
is a characterizing scalar to be determined such that the MSE of the proposed estimator t is minimized. To obtain the bias and Mean squared error of the proposed estimator, we wish to define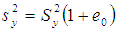 and
and 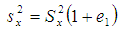 such that
such that 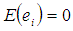 for
for 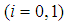 and
and 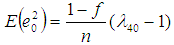 ,
, 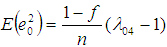 ,
, 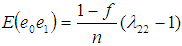 .The proposed estimator
.The proposed estimator 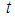 can be written in terms of
can be written in terms of 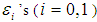 , as
, as 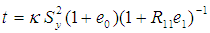 Expanding the right hand side of above equation and considering the terms in
Expanding the right hand side of above equation and considering the terms in 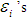 up to the first degree of approximation, we get:
up to the first degree of approximation, we get: 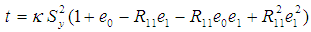 After subtracting the population variance
After subtracting the population variance 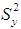 of study variable on both the sides of above equation, we have,
of study variable on both the sides of above equation, we have,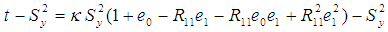 | (3.2) |
The bias of proposed estimator 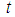 is obtained by taking expectations on both sides of (3.2) and putting the values of different expectations, as:
is obtained by taking expectations on both sides of (3.2) and putting the values of different expectations, as: 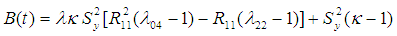 | (3.3) |
where 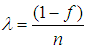 .The mean squared error of the proposed estimator
.The mean squared error of the proposed estimator 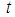 is obtained by squaring both sides of (3.2), simplifying and taking expectation on both sides, up to the first order of approximation as,
is obtained by squaring both sides of (3.2), simplifying and taking expectation on both sides, up to the first order of approximation as,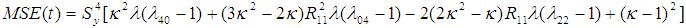 | (3.4) |
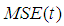 is minimum for,
is minimum for, 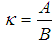 | (3.5) |
where,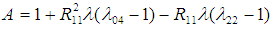 and
and 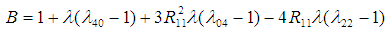 The minimum MSE of the estimator,
The minimum MSE of the estimator, 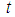 , for this optimum value of
, for this optimum value of 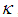 , is:
, is: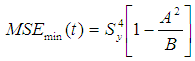 | (3.6) |
4. Efficiency Comparison
The proposed estimator 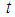 performs better than the estimator
performs better than the estimator 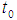 in the sense having lesser mean squared error under the condition:
in the sense having lesser mean squared error under the condition: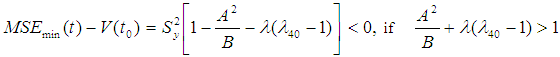 | (4.1) |
The proposed estimator in (3.1) will perform better than the estimator (2.3), under the condition if: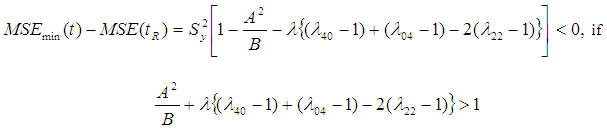 | (4.2) |
The proposed estimator 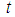 has more efficiency as compared to all other estimators
has more efficiency as compared to all other estimators 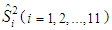 mentioned in this manuscript under the condition if:
mentioned in this manuscript under the condition if: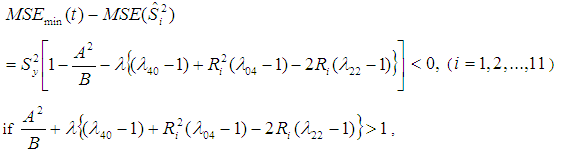 | (4.3) |
5. Numerical Illustration
Following populations have been considered to examine the performances of different estimators of population variance, Population I: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Total amount (tons) of recyclable-waste collection in Italy in 2002.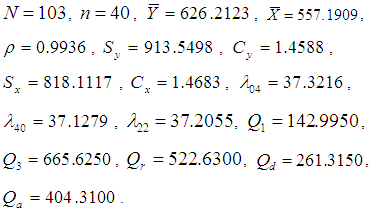 Population II: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Number of inhabitants in 2003.
Population II: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Number of inhabitants in 2003.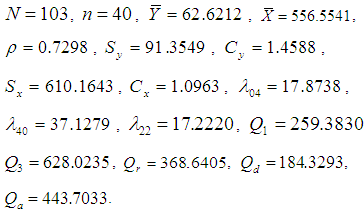 Population III: Murthy (1967) Y: Output for 80 factories in a region.X: Fixed capital.
Population III: Murthy (1967) Y: Output for 80 factories in a region.X: Fixed capital.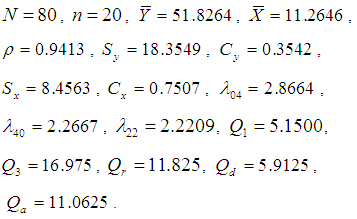 Population IV: Singh and Cahudhary The population consists of 70 wheat farms in 70 villages in certain region of India and the variables under considerations are defined as:Y = area under wheat crop (in acres) during 1974, X = area under wheat crop (in acres) during 1973,
Population IV: Singh and Cahudhary The population consists of 70 wheat farms in 70 villages in certain region of India and the variables under considerations are defined as:Y = area under wheat crop (in acres) during 1974, X = area under wheat crop (in acres) during 1973, 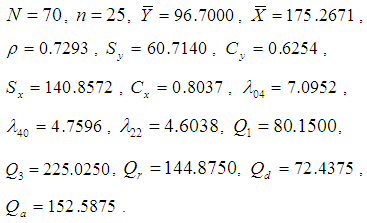
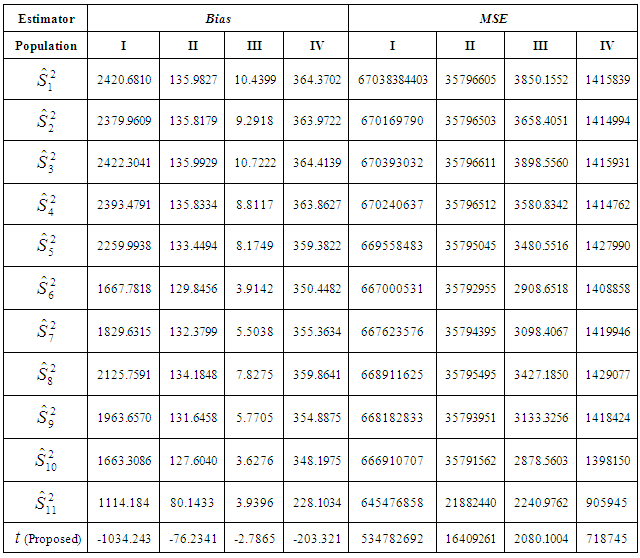
Table 1. Comparison of Bias and Mean square error of different estimators
 |
| |
|
6. Results and Conclusions
This paper deals with the estimation of population variance using improved ratio type estimator. An efficient estimator of population variance using coefficient of correlation and the inter quartile range of the auxiliary variable has been proposed. Up to the first degree of approximation, the expressions for the bias and mean square error of the proposed estimator have been obtained. The optimum value of the characterizing scalar kappa, which minimizes the mean squared error of the proposed estimator, is also obtained. Further the minimum value of the mean square error for this optimum value of kappa has also been obtained. It has been proved theoretically as well as empirically that the proposed estimator performs much better than all of the other mentioned estimators of population variance in the sense of having lesser Bias and MSE. It is of worth to be mentioned that the knowledge regarding the correlation coefficient 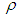 should be available in advance. This knowledge of correlation coefficient is either available in advance (generally) or it is obtained from prior studies like pilot surveys etc. In case if we do not have prior knowledge of correlation coefficient, then it in the expression of estimator is replaced by its estimate and there is no effect on the mean squared error the estimator. Therefore it is strongly recommended that the proposed estimator should be preferred over the estimators mentioned in this manuscript for the estimation of population variance under simple random sampling scheme.
should be available in advance. This knowledge of correlation coefficient is either available in advance (generally) or it is obtained from prior studies like pilot surveys etc. In case if we do not have prior knowledge of correlation coefficient, then it in the expression of estimator is replaced by its estimate and there is no effect on the mean squared error the estimator. Therefore it is strongly recommended that the proposed estimator should be preferred over the estimators mentioned in this manuscript for the estimation of population variance under simple random sampling scheme.
ACKNOWLEDGEMENTS
The authors are very much thankful to the editor in chief of AJOR and the anonymous learned referees for critically examining the manuscript and giving the valuable suggestions for further improvement in the earlier draft.
References
| [1] | Isaki, C, T., Variance estimation using auxiliary information, Journal of American Statistical Association, 78, 117- 123 (1983). |
| [2] | Kadilar, C. and Cingi, H., Improvement in variance estimation using auxiliary information, Hacettepe Journal of mathematics and Statistics, 35, 111-15 (2006). |
| [3] | Kadilar, C. and Cingi, H., Ratio estimators for population variance in simple and Stratified sampling, Applied Mathematics and Computation, 173, 1047-1058 (2006). |
| [4] | Khan, M. and Shabbir, J., A Ratio Type Estimator for the Estimation of Population Variance using Quartiles of an Auxiliary Variable, Journal of Statistics Applications & Probability, 2, 3, 319-325 (2013). |
| [5] | Murthy, M. N., Sampling Theory and Methods, Statistical Publishing Society Calcutta, India, (1967). |
| [6] | Singh, D. and Chaudhary, F. S., Theory and analysis of sample survey designs, New-Age International Publisher, (1986). |
| [7] | Subramani, J. and Kumarapandiyan, G., Variance estimation using quartiles and their functions of an auxiliary variable, International Journal of Statistics and Applications, 2, 67-72 (2012). |
| [8] | Upadhyaya, L. N. and Singh, H. P., Use of auxiliary information in the estimation of population variance, mathematical forum, 4, 33-36 (1983). |
| [9] | http://www.osservatorionalerifiuti.it/ElencoDocPub.asp?A_TipoDoc=6. |
| [10] | Yadav, S.K., Mishra, S.S. and Gupta, S., Improved Variance Estimation Utilizing Correlation Coefficient and Quartiles of an Auxiliary Variable, Communicated to American Journal of Mathematics and Mathematical Sciences, (2014). |



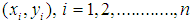 be a random sample of size n from above bivariate population (X, Y) of size N using a SRSWOR scheme. Let
be a random sample of size n from above bivariate population (X, Y) of size N using a SRSWOR scheme. Let 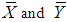 respectively are the population means of the auxiliary and the study variables, and let
respectively are the population means of the auxiliary and the study variables, and let 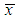 and
and 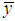 are the corresponding sample means which are unbiased estimators of population means
are the corresponding sample means which are unbiased estimators of population means 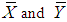 respectively. Let
respectively. Let 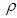 denote the correlation coefficient between the variables X and Y and
denote the correlation coefficient between the variables X and Y and 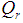 is the inter-quartile range of the auxiliary variable X. In this manuscript, we have proposed an improved ratio type estimator of population variance of study variable by suitably using the correlation coefficient
is the inter-quartile range of the auxiliary variable X. In this manuscript, we have proposed an improved ratio type estimator of population variance of study variable by suitably using the correlation coefficient 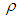 between the two variables and
between the two variables and 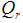 , inter-quartile range of the auxiliary variable X. Further we assume that a reliable estimate of the correlation coefficient
, inter-quartile range of the auxiliary variable X. Further we assume that a reliable estimate of the correlation coefficient 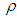 is available in advance from pilot surveys etc.
is available in advance from pilot surveys etc.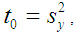
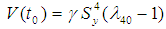
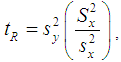
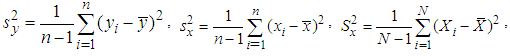
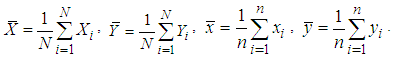 The first order of approximations for the Bias and Mean Square Error (MSE) respectively are given by
The first order of approximations for the Bias and Mean Square Error (MSE) respectively are given by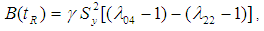
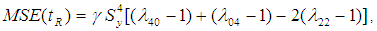
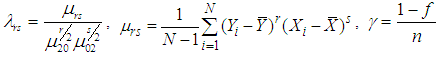 and
and 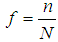 .Several authors proposed different estimators by utilizing auxiliary information in different forms. They used it in the form of different parameters of auxiliary variable for estimating the population variance of the main variable under study. Some of them from the literature are as follows, Upadhyaya and Singh (1999) utilized coefficient of kurtosis
.Several authors proposed different estimators by utilizing auxiliary information in different forms. They used it in the form of different parameters of auxiliary variable for estimating the population variance of the main variable under study. Some of them from the literature are as follows, Upadhyaya and Singh (1999) utilized coefficient of kurtosis 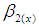 of auxiliary variable and proposed the following estimator of population variance as,
of auxiliary variable and proposed the following estimator of population variance as,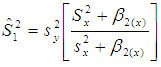
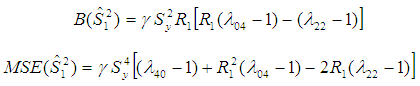
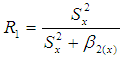 Kadilar and Cingi (2006) proposed the following estimators using different parameters of auxiliary information as,
Kadilar and Cingi (2006) proposed the following estimators using different parameters of auxiliary information as,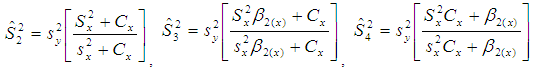 The bias and Mean Squared Error of above estimators up to the first order of approximations respectively are,
The bias and Mean Squared Error of above estimators up to the first order of approximations respectively are, 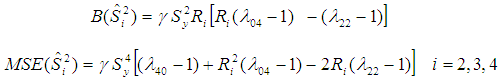
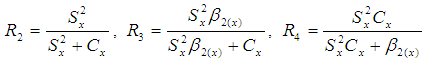 Subramani and Kumarpandiyan (2012), utilizing various population parameters of auxiliary variable proposed the following estimators of population variance as,
Subramani and Kumarpandiyan (2012), utilizing various population parameters of auxiliary variable proposed the following estimators of population variance as,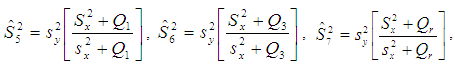
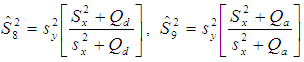 The expressions for the bias and Mean Squared Error of above estimators up to the first order of approximations respectively are,
The expressions for the bias and Mean Squared Error of above estimators up to the first order of approximations respectively are, 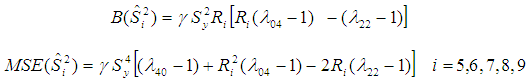
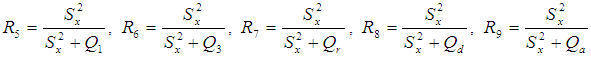 Where
Where 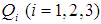 are the quartiles, the three points dividing the whole distribution into four equal parts. Further the functions of quartiles are, the inter quartile range,
are the quartiles, the three points dividing the whole distribution into four equal parts. Further the functions of quartiles are, the inter quartile range, 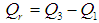 , the semi-quartile range
, the semi-quartile range 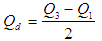 and the quartile average
and the quartile average 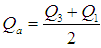 . Khan and Shabbir (2013) proposed the following estimator using correlation coefficient and the third quartile of the auxiliary variable as,
. Khan and Shabbir (2013) proposed the following estimator using correlation coefficient and the third quartile of the auxiliary variable as,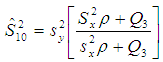 The expressions for the bias and Mean Squared Error of the estimator up to the first order of approximations respectively are,
The expressions for the bias and Mean Squared Error of the estimator up to the first order of approximations respectively are, 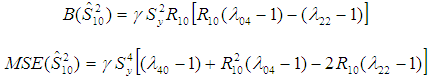
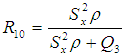 Yadav et al. (2014), utilizing the correlation coefficient of the inter-quartile range of auxiliary variable proposed the following estimator as,
Yadav et al. (2014), utilizing the correlation coefficient of the inter-quartile range of auxiliary variable proposed the following estimator as,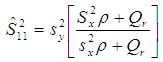 The bias and Mean Squared Error of the above estimator up to the first order of approximations respectively are,
The bias and Mean Squared Error of the above estimator up to the first order of approximations respectively are,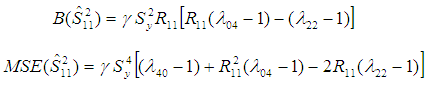
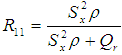 .
.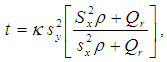
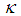 is a characterizing scalar to be determined such that the MSE of the proposed estimator t is minimized. To obtain the bias and Mean squared error of the proposed estimator, we wish to define
is a characterizing scalar to be determined such that the MSE of the proposed estimator t is minimized. To obtain the bias and Mean squared error of the proposed estimator, we wish to define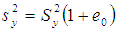 and
and 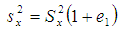 such that
such that 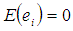 for
for 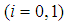 and
and 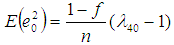 ,
, 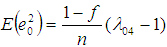 ,
, 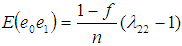 .The proposed estimator
.The proposed estimator 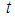 can be written in terms of
can be written in terms of 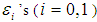 , as
, as 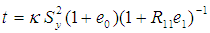 Expanding the right hand side of above equation and considering the terms in
Expanding the right hand side of above equation and considering the terms in 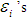 up to the first degree of approximation, we get:
up to the first degree of approximation, we get: 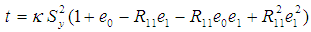 After subtracting the population variance
After subtracting the population variance 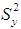 of study variable on both the sides of above equation, we have,
of study variable on both the sides of above equation, we have,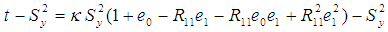
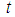 is obtained by taking expectations on both sides of (3.2) and putting the values of different expectations, as:
is obtained by taking expectations on both sides of (3.2) and putting the values of different expectations, as: 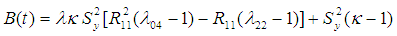
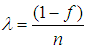 .The mean squared error of the proposed estimator
.The mean squared error of the proposed estimator 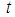 is obtained by squaring both sides of (3.2), simplifying and taking expectation on both sides, up to the first order of approximation as,
is obtained by squaring both sides of (3.2), simplifying and taking expectation on both sides, up to the first order of approximation as,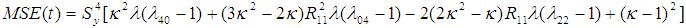
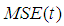 is minimum for,
is minimum for, 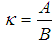
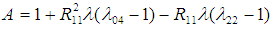 and
and 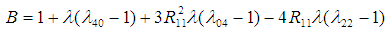 The minimum MSE of the estimator,
The minimum MSE of the estimator, 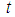 , for this optimum value of
, for this optimum value of 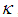 , is:
, is: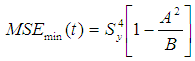
 performs better than the estimator
performs better than the estimator  in the sense having lesser mean squared error under the condition:
in the sense having lesser mean squared error under the condition: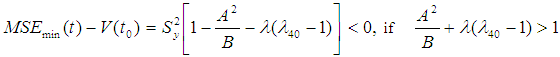
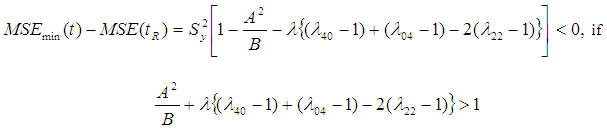
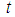 has more efficiency as compared to all other estimators
has more efficiency as compared to all other estimators 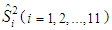 mentioned in this manuscript under the condition if:
mentioned in this manuscript under the condition if: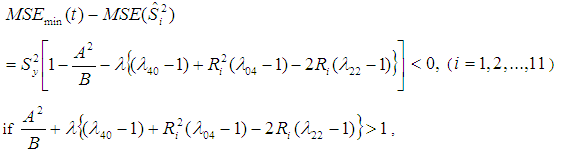
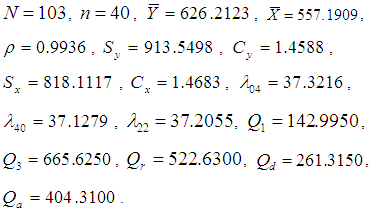 Population II: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Number of inhabitants in 2003.
Population II: Italian bureau for the environment protection-APAT Waste 2004 Y: Total amount (tons) of recyclable-waste collection in Italy in 2003.X: Number of inhabitants in 2003.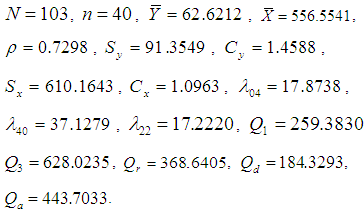 Population III: Murthy (1967) Y: Output for 80 factories in a region.X: Fixed capital.
Population III: Murthy (1967) Y: Output for 80 factories in a region.X: Fixed capital.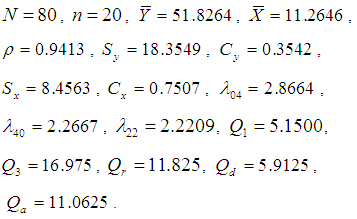 Population IV: Singh and Cahudhary The population consists of 70 wheat farms in 70 villages in certain region of India and the variables under considerations are defined as:Y = area under wheat crop (in acres) during 1974, X = area under wheat crop (in acres) during 1973,
Population IV: Singh and Cahudhary The population consists of 70 wheat farms in 70 villages in certain region of India and the variables under considerations are defined as:Y = area under wheat crop (in acres) during 1974, X = area under wheat crop (in acres) during 1973, 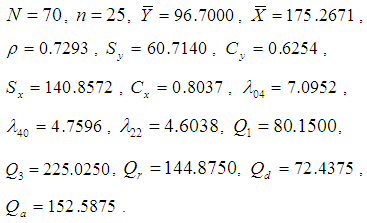
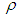 should be available in advance. This knowledge of correlation coefficient is either available in advance (generally) or it is obtained from prior studies like pilot surveys etc. In case if we do not have prior knowledge of correlation coefficient, then it in the expression of estimator is replaced by its estimate and there is no effect on the mean squared error the estimator. Therefore it is strongly recommended that the proposed estimator should be preferred over the estimators mentioned in this manuscript for the estimation of population variance under simple random sampling scheme.
should be available in advance. This knowledge of correlation coefficient is either available in advance (generally) or it is obtained from prior studies like pilot surveys etc. In case if we do not have prior knowledge of correlation coefficient, then it in the expression of estimator is replaced by its estimate and there is no effect on the mean squared error the estimator. Therefore it is strongly recommended that the proposed estimator should be preferred over the estimators mentioned in this manuscript for the estimation of population variance under simple random sampling scheme.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML