Subhash Kumar Yadav1, S. S. Mishra1, Cem Kadilar2, Alok Kumar Shukla3
1Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India
2Department of Statistics, Hacettepe University, Beytepe, Ankara, Turkey
3Department of Statistics, D.A-V College, Kanpur, U.P., India
Correspondence to: S. S. Mishra, Department of Mathematics and Statistics (A Centre of Excellence), Dr. RML Avadh University, Faizabad, U.P., India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this article, we propose an improved dual to ratio cum dual to product estimator of the population mean under the stratified random sampling scheme. The expressions for the bias and mean squared error (MSE) of the proposed estimator are found by the first degree of approximation. The optimum value of the constant, which minimizes the MSE of the proposed estimator, is also obtained. Efficiency comparisons are performed between the proposed estimator and many estimators in Literature under the stratified random sampling and the efficiency conditions of the proposed estimator are determined. Finally, an empirical study is carried out which shows the performance of the proposed estimator along with the existing estimators under the stratified random sampling.
Keywords:
Ratio and Product estimators, Stratified Random Sampling, Bias, MSE, Efficiency
Cite this paper: Subhash Kumar Yadav, S. S. Mishra, Cem Kadilar, Alok Kumar Shukla, Improved Dual to Ratio Cum Dual to Product Estimator in the Stratified Random Sampling, American Journal of Operational Research, Vol. 5 No. 3, 2015, pp. 57-63. doi: 10.5923/j.ajor.20150503.02.
1. Introduction
In practice, it is very common that the use of the auxiliary variable (x or z) improves the efficiency of the estimators for the population parameters of the study variable (y). The auxiliary information supplied by the auxiliary variables is used both at the design and estimation stages of the survey. We have used it in the estimation stage in this article. The auxiliary variable is highly correlated (positively or negatively) with the study variable. The ratio method of estimation providing ratio type estimators is used for the estimation of population parameters when the study variable and the auxiliary variables are highly positively correlated to each other; whereas, the product method of estimation giving product type estimators is used when y and x are highly negatively correlated to each other. As in practice, we find that the study variable has both positive and negative correlations with two different variables at a time. This encourages us to use both positively and negatively correlated variables in our study and we propose the dual to ratio and dual to product estimator of the population mean in the stratified random sampling. The improvement is a continuous process of research and the form of the estimator using the scalar 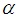 has always improved the estimators of population parameters in the simple random sampling. Being inspired from this truth, we have proposed the dual to ratio and dual to product estimator of the population mean in the stratified random sampling.As we deal with the methods in the stratified random sampling, assume that the finite population,
has always improved the estimators of population parameters in the simple random sampling. Being inspired from this truth, we have proposed the dual to ratio and dual to product estimator of the population mean in the stratified random sampling.As we deal with the methods in the stratified random sampling, assume that the finite population, 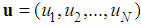 , consists of
, consists of 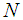 distinct and identifiable units which are heterogeneous from each other. Let the whole population be divided into
distinct and identifiable units which are heterogeneous from each other. Let the whole population be divided into 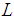 strata of sizes,
strata of sizes, 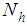
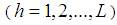 , in which units are relatively homogeneous to each other. In addition, the study variable, y, and two auxiliary variables, x and z, take the values
, in which units are relatively homogeneous to each other. In addition, the study variable, y, and two auxiliary variables, x and z, take the values 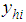 ,
, 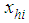 , and
, and 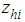
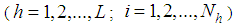 , respectively, for the
, respectively, for the 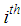 unit of the
unit of the 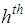 stratum. It is clear that the sub-samples of sizes,
stratum. It is clear that the sub-samples of sizes, 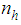
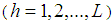 , are drawn from each stratum using the proportional allocation method, constituting of the required sample of size as
, are drawn from each stratum using the proportional allocation method, constituting of the required sample of size as 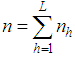 .Following common notations of the stratified random sampling, it can be given by
.Following common notations of the stratified random sampling, it can be given by 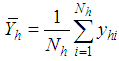 : The
: The 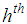 stratum population mean for the study variable,
stratum population mean for the study variable, 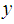 ,
,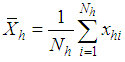 : The
: The 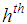 stratum population mean for the auxiliary variable,
stratum population mean for the auxiliary variable, 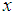 ,
,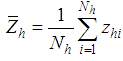 : The
: The 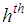 stratum population mean for the auxiliary variable,
stratum population mean for the auxiliary variable, 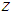 ,
,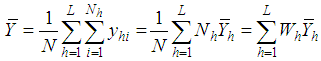 : The population mean of the study variable,
: The population mean of the study variable, 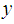 ,
,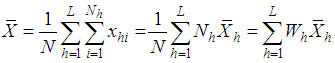 : The population mean of the auxiliary variable,
: The population mean of the auxiliary variable, 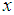 ,
,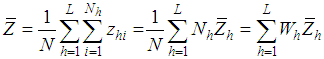 : The population mean of the auxiliary variable,
: The population mean of the auxiliary variable, 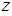 ,
,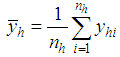 : The
: The 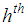 stratum sample mean of the study variable,
stratum sample mean of the study variable, 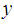 ,
, 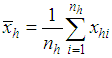 : The
: The 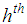 stratum sample mean of the auxiliary variable,
stratum sample mean of the auxiliary variable, 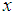 ,
, 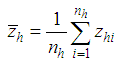 : The
: The 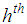 stratum sample mean of the auxiliary variable,
stratum sample mean of the auxiliary variable, 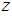 ,
, 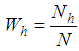 : Weight of the
: Weight of the 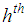 stratum.
stratum.
2. Estimators in Literature
Hansen et al. [1] proposed the classical combined ratio estimator for the population mean under the stratified random sampling as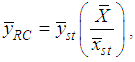 | (2.1) |
where 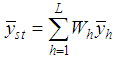 and
and 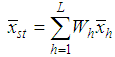 .The MSE of the combined ratio estimator in (2.1), up to the first order of approximation, is
.The MSE of the combined ratio estimator in (2.1), up to the first order of approximation, is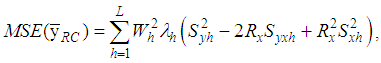 | (2.2) |
where 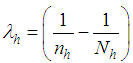 ,
, 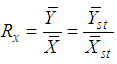 is the population ratio,
is the population ratio, 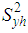 is the population variance of the study variable,
is the population variance of the study variable, 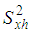 is the population variance of the auxiliary variable, and
is the population variance of the auxiliary variable, and 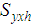 is the population covariance between the study and auxiliary variables in the
is the population covariance between the study and auxiliary variables in the 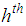 stratum.The combined product estimator of the population mean in the stratified random sampling is defined as
stratum.The combined product estimator of the population mean in the stratified random sampling is defined as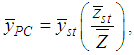 | (2.3) |
where 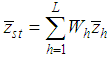 .The MSE of the combined product estimator in (2.3), up to the first order of approximation, is
.The MSE of the combined product estimator in (2.3), up to the first order of approximation, is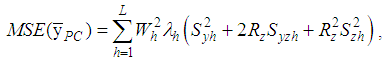 | (2.4) |
where 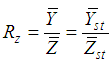 .Many authors, such as Kadilar and Cingi ([2], [3]), Shabbir and Gupta [4], Singh and Vishwakarma [5], Koyuncu and Kadilar ([6], [7], [8], [9]), Sanaullah et al. [10] have improved the ratio and product estimators, given in (2.1) and (2.3), for the population mean of the study variable in the stratified random sampling. However, in this article, we examine only dual estimators for the population mean in Literature that can be summarized as follows:Using the combined ratio and product estimators, Kushwaha et al. [11] proposed the following dual to ratio and dual to product estimators by the Srivenkataramana [12] transformation as
.Many authors, such as Kadilar and Cingi ([2], [3]), Shabbir and Gupta [4], Singh and Vishwakarma [5], Koyuncu and Kadilar ([6], [7], [8], [9]), Sanaullah et al. [10] have improved the ratio and product estimators, given in (2.1) and (2.3), for the population mean of the study variable in the stratified random sampling. However, in this article, we examine only dual estimators for the population mean in Literature that can be summarized as follows:Using the combined ratio and product estimators, Kushwaha et al. [11] proposed the following dual to ratio and dual to product estimators by the Srivenkataramana [12] transformation as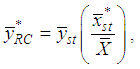 | (2.5) |
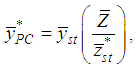 | (2.6) |
respectively, where 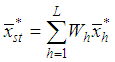 and
and 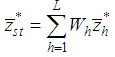 . Here, the Srivenkataramana [12] transformations are
. Here, the Srivenkataramana [12] transformations are 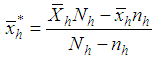 and
and 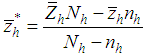 .The MSE of dual to ratio and dual to product estimators in (2.5) and (2.6), respectively, up to the first order of approximation, are, respectively, given by
.The MSE of dual to ratio and dual to product estimators in (2.5) and (2.6), respectively, up to the first order of approximation, are, respectively, given by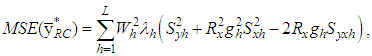 | (2.7) |
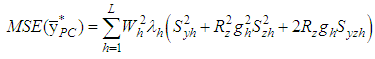 | (2.8) |
where 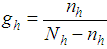 .Singh et al. [13] suggested following exponential ratio and product type estimators in the stratified random sampling based on Bahl and Tuteja [14] estimators of the population mean under the simple random sampling, respectively, as follows:
.Singh et al. [13] suggested following exponential ratio and product type estimators in the stratified random sampling based on Bahl and Tuteja [14] estimators of the population mean under the simple random sampling, respectively, as follows: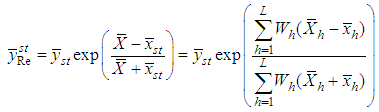 | (2.9) |
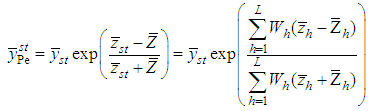 | (2.10) |
The MSE of the estimators in (2.9) and (2.10), up to the first order of approximation, are, respectively,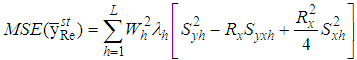 | (2.11) |
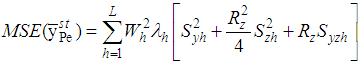 | (2.12) |
Tailor et al. [15] proposed the following dual to ratio and product type estimators using the Singh et al. [13] estimators as follows: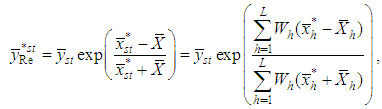 | (2.13) |
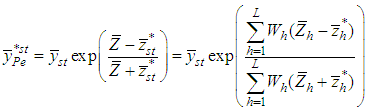 | (2.14) |
The MSE of the estimators in (2.13) and (2.14), up to the first order of approximation are, respectively,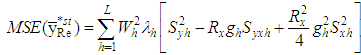 | (2.15) |
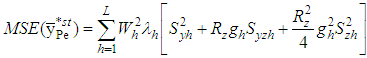 | (2.16) |
3. Proposed Estimator
Motivated by the estimators, mentioned in Section 2 and the fact that the use of a scalar in the current forms (2.13) and (2.14) always improves the estimator, we propose the following dual to ratio cum dual to product estimator of the population mean in the stratified random sampling by combining the dual to ratio and dual to product estimators as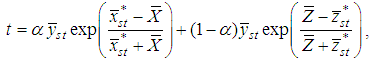 | (3.1) |
where 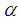 is a suitable constant to be determined such that the MSE of the proposed estimator,
is a suitable constant to be determined such that the MSE of the proposed estimator, 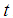 , is minimum.It is worth notable that it becomes the dual to product estimator, given in (2.14), for
, is minimum.It is worth notable that it becomes the dual to product estimator, given in (2.14), for 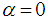 and that it reduces to dual to ratio estimator, given in (2.13), for
and that it reduces to dual to ratio estimator, given in (2.13), for 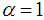 .To study the large sample properties of the proposed estimator,
.To study the large sample properties of the proposed estimator, 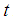 , let us define the following notations:
, let us define the following notations: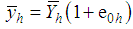 ,
, 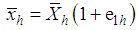 , and
, and 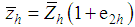 such that
such that 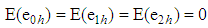 and
and 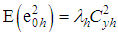 ,
, 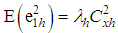 ,
, 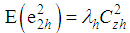 ,
, 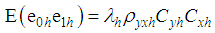 ,
, 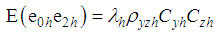 ,
, 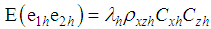 .Expressing the proposed estimator, in (3.1), in terms of
.Expressing the proposed estimator, in (3.1), in terms of 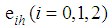 , we have
, we have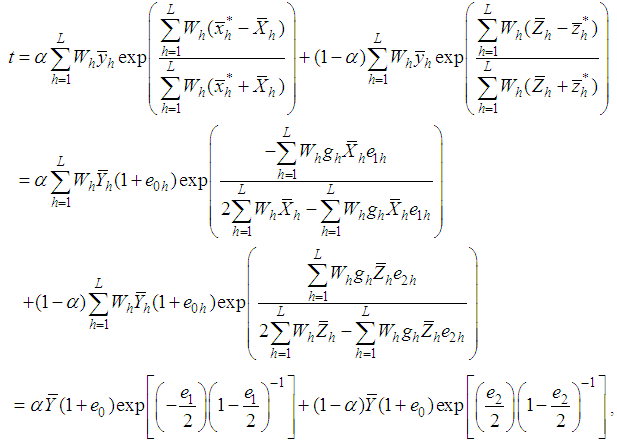 | (3.2) |
where 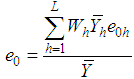 ,
, 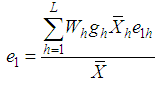 , and
, and 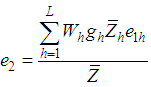 such that
such that  and
and 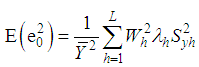 ,
, 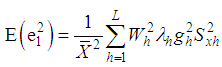 ,
, 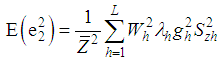 ,
, 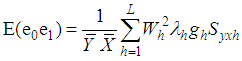 ,
, 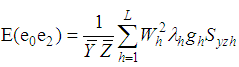 ,
, 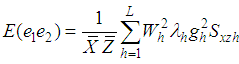 .On simplifying the expressions after the expansion on the right hand side of (3.2), up to the first order of approximation, we have
.On simplifying the expressions after the expansion on the right hand side of (3.2), up to the first order of approximation, we have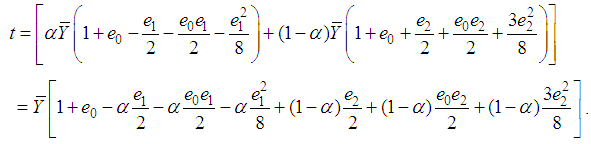 | (3.3) |
We can write (3.3) as 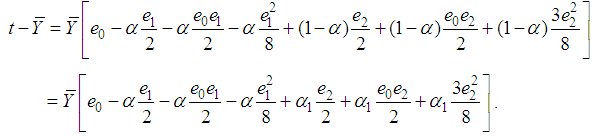 | (3.4) |
Taking the expectation on both sides of (3.4), we have the bias of the proposed estimator, up to the first order of approximation, as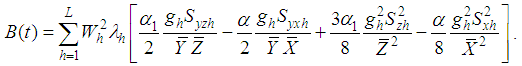 | (3.5) |
From (3.4), up to the first order of approximation, the MSE of the proposed estimator is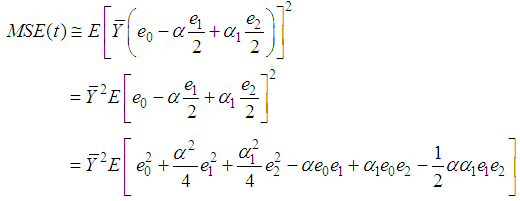 | (3.6) |
which is minimum for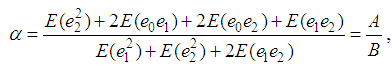 where
where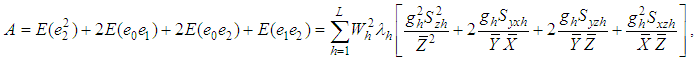
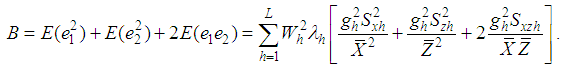 Finally, the minimum MSE of the proposed estimator is
Finally, the minimum MSE of the proposed estimator is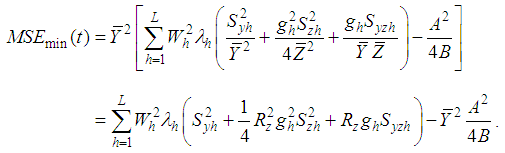 | (3.7) |
4. Efficiency Comparisons
The variance of the sample mean in the stratified random sampling, 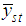 , is given by
, is given by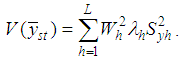 | (4.1) |
We obtain the following conditions under which the proposed dual to ratio cum dual to product type exponential estimator is better than the estimators, 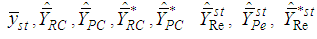 , and
, and 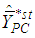 , respectively.The proposed estimator,
, respectively.The proposed estimator, 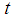 , is more efficient than
, is more efficient than 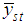 if
if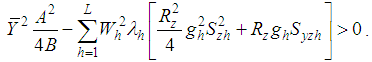 | (4.2) |
It is more efficient than the estimator, 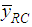 , if
, if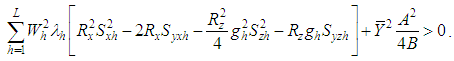 | (4.3) |
It is more efficient than the estimator, 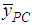 , if
, if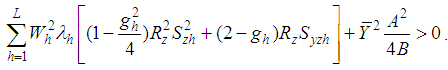 | (4.4) |
It is more efficient than the estimator, 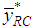 , if
, if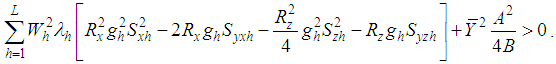 | (4.5) |
It is more efficient than the estimator,  , if
, if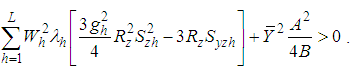 | (4.6) |
 is more efficient than
is more efficient than 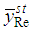 if
if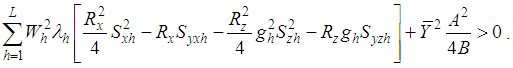 | (4.7) |
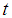 is more efficient than
is more efficient than 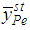 if
if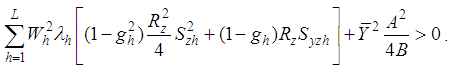 | (4.8) |
The proposed estimator,  , is more efficient than
, is more efficient than  if
if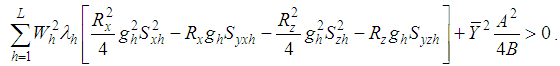 | (4.9) |
The proposed estimator, 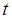 , is more efficient than
, is more efficient than 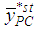 if
if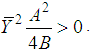 | (4.10) |
5. Empirical Study
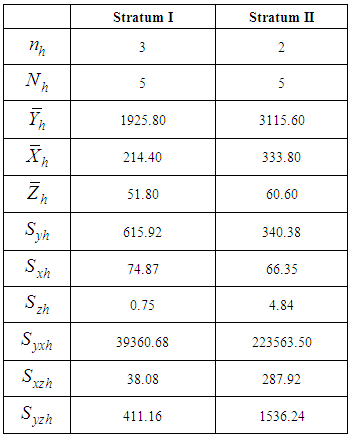
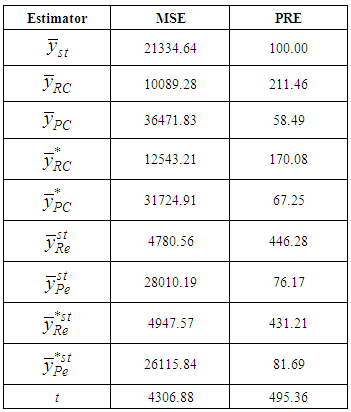
To examine the efficiency of the proposed estimator over other estimators, we consider the data set in Murthy [16] whose statistics are given in Table 1. The MSE and percent relative efficiency (PRE) values are given in Table 2. Table 1. Data Statistics
 |
| |
|
Table 2. MSE and PRE Values of Estimators
 |
| |
|
We wish to elaborate the tabulated values in various columns of the Table 1. In the first column of the table, the various parameters of main and auxiliary variables, such as population size, sample size, population means, variances and covariances of both strata, respectively, have been given. Second and third columns present respective parameter values for first and second strata. Table 2 presents the mean square error and the Percentage Relative Efficiency (PRE) for the existing and the proposed estimators. The PRE of an estimator with respect to the sample mean is defined by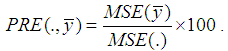
6. Conclusions
Sample surveys are legitimately considered as cost effective apparatus for estimation of the population parameter. The Statistician wishes to minimize the mean square error of the estimator to ideally infer about the parameter of the given population. In the present problem, we have proposed a dual to ratio cum dual to product estimator of population mean in stratified random sampling as in many situations we need both positively and negatively correlated information with the main variable under study. Further large sample properties of the proposed estimator have been studied up to the first order of approximation. We have also made the comparisons of desired results with previous researchers. Finally we have judged the performances of different estimators along with the proposed estimator through an empirical study under stratified random sampling. From the theoretical discussion and the numerical results from Table 2, we conclude that the proposed estimator is better than the mentioned estimators, in Section 2, under the stratified random sampling scheme as the proposed estimator has smaller mean squared error. By this numerical example, we also show that the efficiency conditions in theory for the proposed estimator, obtained in (4.2)-(4.10), are satisfied in practice, as well. Thus, the proposed estimator should be preferred for the estimation of the population mean under the stratified random sampling.
References
| [1] | Hansen, M.H., Hurwitz, W.N., and Gurney, M. (1946) Problem and Methods of the Sample Survey of Business, JASA, 41, 174-189. |
| [2] | Kadilar, C. and Cingi, H. (2003) Ratio Estimators in Stratified Random Sampling, Biometrical Journal, 45, 2, 218-225. |
| [3] | Kadilar, C. and Cingi, H. (2005) A New Ratio Estimator in Stratified Random Sampling, Communications in Statistics: Theory and Methods, 34, 3, 597-602. |
| [4] | Shabbir, J. and Gupta, S. (2006) A New Estimator of Population Mean in Stratified Sampling, Communications in Statistics: Theory and Methods, 35, 1201-1209. |
| [5] | Singh, H.P. and Vishwakarma, G.K. (2008) A Family of Estimators of Population Mean Using Auxiliary Information in Stratified Sampling, Communications in Statistics: Theory and Methods, 37, 7, 1038–1050. |
| [6] | Koyuncu, N. and Kadilar, C. (2009a) Ratio and Product Estimators in Stratified Random Sampling, Journal of Statistical Planning and Inference, 139, 8, 2552-2558. |
| [7] | Koyuncu, N. and Kadilar, C. (2009b) Family of Estimators of Population Mean Using Two Auxiliary Variables in Stratified Random Sampling, Communications in Statistics: Theory and Methods, 38, 14, 2398-2417. |
| [8] | Koyuncu, N. and Kadilar, C. (2010a) On Improvement in Estimating Population Mean in Stratified Random Sampling, Journal of Applied Statistics, 37, 6, 999-1013. |
| [9] | Koyuncu, N. and Kadilar, C. (2010b) On the Family of Estimators of Population Mean in Stratified Random Sampling, Pakistan Journal of Statistics, 26, 2, 427-443. |
| [10] | Sanaullah, A., Ali, H. A., Noor ul Amin, M., and Hanif, M. (2014) Generalized exponential chain ratio estimators under stratified two-phase random sampling, Applied Mathematics and Computation, 226, 1, 541-547. |
| [11] | Kushwaha, K.S., Upadhyaya, L.N., and Dubey, S.P. (1990) A Dual to Ratio Estimator in Stratified Random Sampling, Proc. Math. Soc., 6, 11-15. |
| [12] | Srivenkataramana, T. (1980) A Dual to Ratio Estimator in Sample Surveys, Biometrika, 67, 199-204. |
| [13] | Singh, R., Chauhan, P., and Sawan, N. (2008) On Linear Combination of Ratio-Product Type Exponential Estimator for Estimating Finite Population Mean, Statistics in Transition, 9, 1, 105-115. |
| [14] | Bahl, S. and Tuteja, R.K. (1991) Ratio and Product Type Exponential Estimator, Information and Optimization Sciences XII, I, 159-163. |
| [15] | Tailor, R., Jatwa, N.K., Tailor, R., and Garg, N. (2013) Dual to Ratio and Product Type Exponential Estimators in Stratified Random Sampling Using Two Auxiliary Variates, Journal of Reliability and Statistical Studies, 6, 2, 115-126. |
| [16] | Murthy, M.N. (1967) Sampling Theory and Methods, Statistical Publishing Society, Calcutta. |

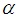 has always improved the estimators of population parameters in the simple random sampling. Being inspired from this truth, we have proposed the dual to ratio and dual to product estimator of the population mean in the stratified random sampling.As we deal with the methods in the stratified random sampling, assume that the finite population,
has always improved the estimators of population parameters in the simple random sampling. Being inspired from this truth, we have proposed the dual to ratio and dual to product estimator of the population mean in the stratified random sampling.As we deal with the methods in the stratified random sampling, assume that the finite population, 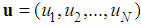 , consists of
, consists of 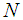 distinct and identifiable units which are heterogeneous from each other. Let the whole population be divided into
distinct and identifiable units which are heterogeneous from each other. Let the whole population be divided into 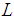 strata of sizes,
strata of sizes, 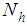
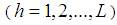 , in which units are relatively homogeneous to each other. In addition, the study variable, y, and two auxiliary variables, x and z, take the values
, in which units are relatively homogeneous to each other. In addition, the study variable, y, and two auxiliary variables, x and z, take the values 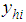 ,
, 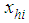 , and
, and 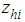
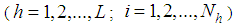 , respectively, for the
, respectively, for the 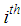 unit of the
unit of the 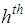 stratum. It is clear that the sub-samples of sizes,
stratum. It is clear that the sub-samples of sizes, 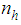
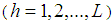 , are drawn from each stratum using the proportional allocation method, constituting of the required sample of size as
, are drawn from each stratum using the proportional allocation method, constituting of the required sample of size as 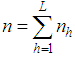 .Following common notations of the stratified random sampling, it can be given by
.Following common notations of the stratified random sampling, it can be given by 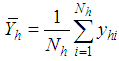 : The
: The 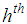 stratum population mean for the study variable,
stratum population mean for the study variable, 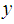 ,
,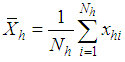 : The
: The 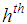 stratum population mean for the auxiliary variable,
stratum population mean for the auxiliary variable, 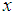 ,
,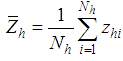 : The
: The 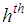 stratum population mean for the auxiliary variable,
stratum population mean for the auxiliary variable, 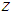 ,
,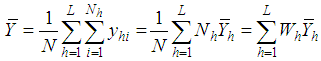 : The population mean of the study variable,
: The population mean of the study variable, 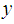 ,
,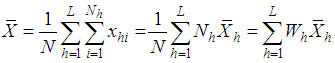 : The population mean of the auxiliary variable,
: The population mean of the auxiliary variable, 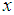 ,
,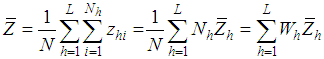 : The population mean of the auxiliary variable,
: The population mean of the auxiliary variable, 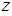 ,
,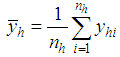 : The
: The 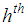 stratum sample mean of the study variable,
stratum sample mean of the study variable, 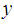 ,
, 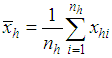 : The
: The 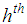 stratum sample mean of the auxiliary variable,
stratum sample mean of the auxiliary variable, 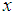 ,
, 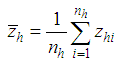 : The
: The 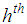 stratum sample mean of the auxiliary variable,
stratum sample mean of the auxiliary variable, 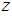 ,
, 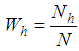 : Weight of the
: Weight of the 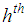 stratum.
stratum.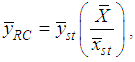
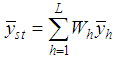 and
and 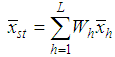 .The MSE of the combined ratio estimator in (2.1), up to the first order of approximation, is
.The MSE of the combined ratio estimator in (2.1), up to the first order of approximation, is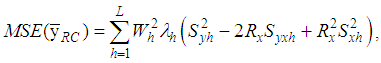
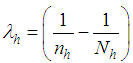 ,
, 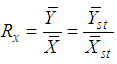 is the population ratio,
is the population ratio, 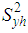 is the population variance of the study variable,
is the population variance of the study variable, 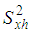 is the population variance of the auxiliary variable, and
is the population variance of the auxiliary variable, and 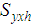 is the population covariance between the study and auxiliary variables in the
is the population covariance between the study and auxiliary variables in the 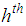 stratum.The combined product estimator of the population mean in the stratified random sampling is defined as
stratum.The combined product estimator of the population mean in the stratified random sampling is defined as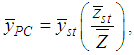
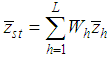 .The MSE of the combined product estimator in (2.3), up to the first order of approximation, is
.The MSE of the combined product estimator in (2.3), up to the first order of approximation, is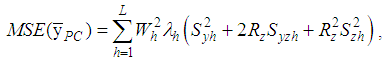
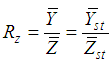 .Many authors, such as Kadilar and Cingi ([2], [3]), Shabbir and Gupta [4], Singh and Vishwakarma [5], Koyuncu and Kadilar ([6], [7], [8], [9]), Sanaullah et al. [10] have improved the ratio and product estimators, given in (2.1) and (2.3), for the population mean of the study variable in the stratified random sampling. However, in this article, we examine only dual estimators for the population mean in Literature that can be summarized as follows:Using the combined ratio and product estimators, Kushwaha et al. [11] proposed the following dual to ratio and dual to product estimators by the Srivenkataramana [12] transformation as
.Many authors, such as Kadilar and Cingi ([2], [3]), Shabbir and Gupta [4], Singh and Vishwakarma [5], Koyuncu and Kadilar ([6], [7], [8], [9]), Sanaullah et al. [10] have improved the ratio and product estimators, given in (2.1) and (2.3), for the population mean of the study variable in the stratified random sampling. However, in this article, we examine only dual estimators for the population mean in Literature that can be summarized as follows:Using the combined ratio and product estimators, Kushwaha et al. [11] proposed the following dual to ratio and dual to product estimators by the Srivenkataramana [12] transformation as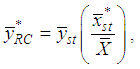
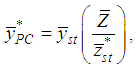
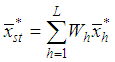 and
and 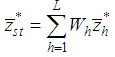 . Here, the Srivenkataramana [12] transformations are
. Here, the Srivenkataramana [12] transformations are 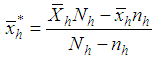 and
and 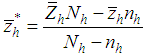 .The MSE of dual to ratio and dual to product estimators in (2.5) and (2.6), respectively, up to the first order of approximation, are, respectively, given by
.The MSE of dual to ratio and dual to product estimators in (2.5) and (2.6), respectively, up to the first order of approximation, are, respectively, given by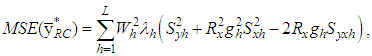
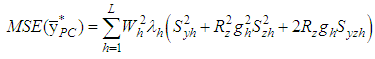
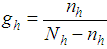 .Singh et al. [13] suggested following exponential ratio and product type estimators in the stratified random sampling based on Bahl and Tuteja [14] estimators of the population mean under the simple random sampling, respectively, as follows:
.Singh et al. [13] suggested following exponential ratio and product type estimators in the stratified random sampling based on Bahl and Tuteja [14] estimators of the population mean under the simple random sampling, respectively, as follows: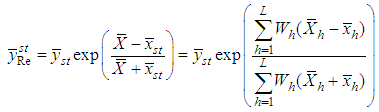
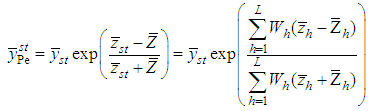
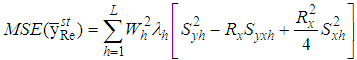
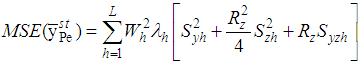
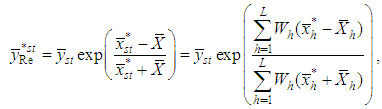
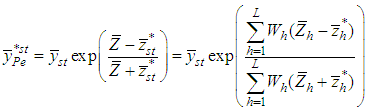
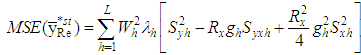
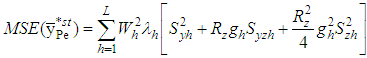
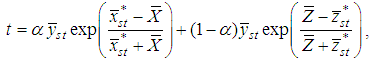
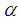 is a suitable constant to be determined such that the MSE of the proposed estimator,
is a suitable constant to be determined such that the MSE of the proposed estimator, 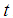 , is minimum.It is worth notable that it becomes the dual to product estimator, given in (2.14), for
, is minimum.It is worth notable that it becomes the dual to product estimator, given in (2.14), for 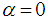 and that it reduces to dual to ratio estimator, given in (2.13), for
and that it reduces to dual to ratio estimator, given in (2.13), for 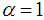 .To study the large sample properties of the proposed estimator,
.To study the large sample properties of the proposed estimator, 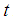 , let us define the following notations:
, let us define the following notations: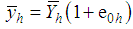 ,
, 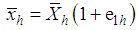 , and
, and 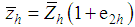 such that
such that 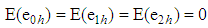 and
and 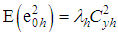 ,
, 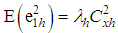 ,
, 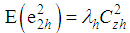 ,
, 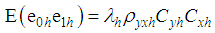 ,
, 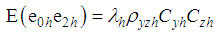 ,
, 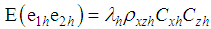 .Expressing the proposed estimator, in (3.1), in terms of
.Expressing the proposed estimator, in (3.1), in terms of 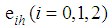 , we have
, we have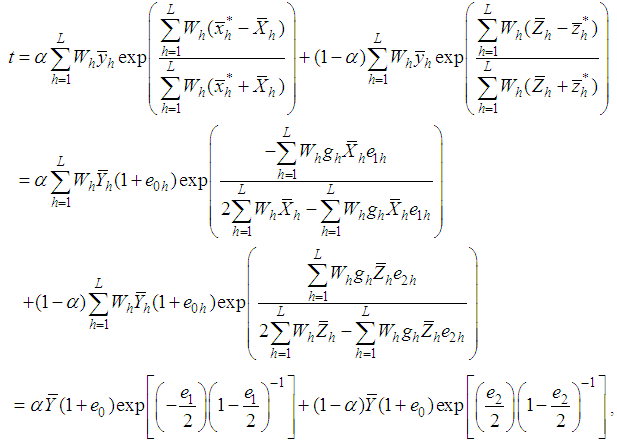
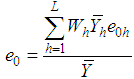 ,
, 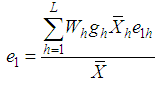 , and
, and 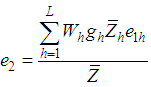 such that
such that 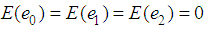 and
and 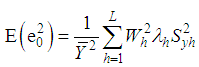 ,
, 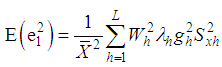 ,
, 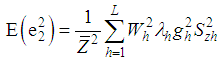 ,
, 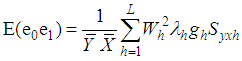 ,
, 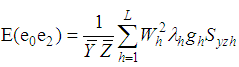 ,
, 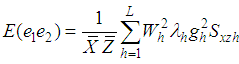 .On simplifying the expressions after the expansion on the right hand side of (3.2), up to the first order of approximation, we have
.On simplifying the expressions after the expansion on the right hand side of (3.2), up to the first order of approximation, we have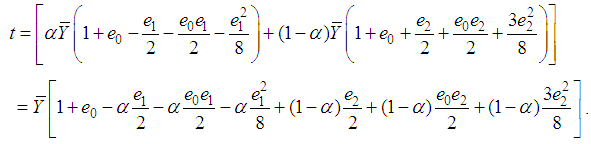
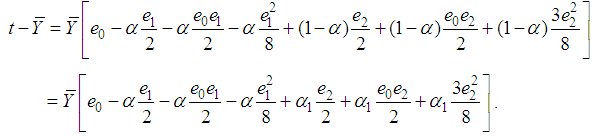
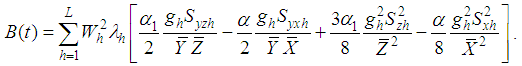
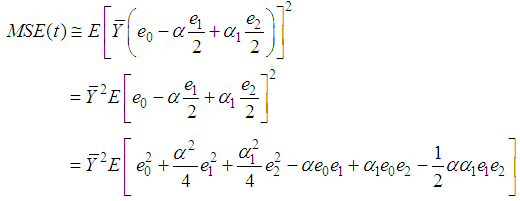
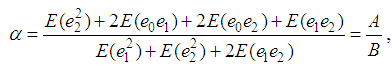 where
where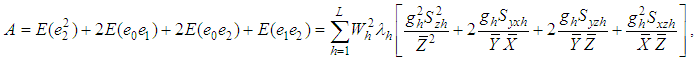
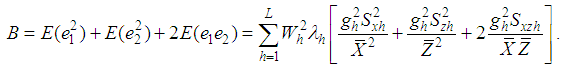 Finally, the minimum MSE of the proposed estimator is
Finally, the minimum MSE of the proposed estimator is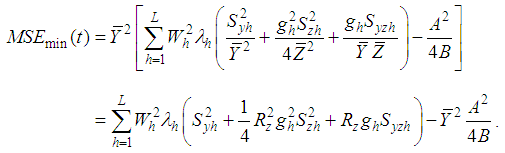
 , is given by
, is given by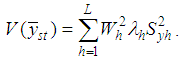
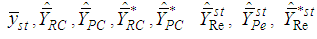 , and
, and 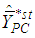 , respectively.The proposed estimator,
, respectively.The proposed estimator, 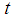 , is more efficient than
, is more efficient than 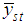 if
if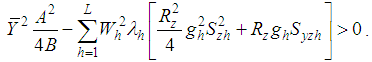
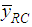 , if
, if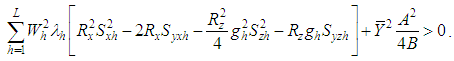
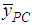 , if
, if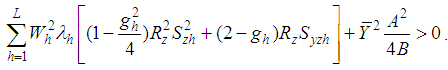
 , if
, if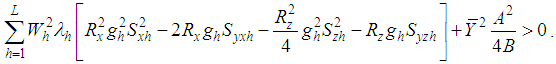
 , if
, if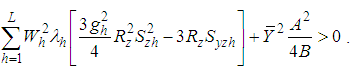
 is more efficient than
is more efficient than  if
if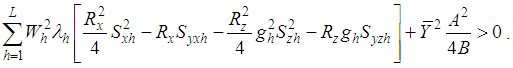
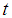 is more efficient than
is more efficient than 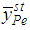 if
if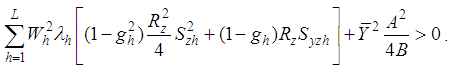
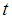 , is more efficient than
, is more efficient than 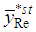 if
if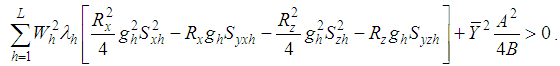
 , is more efficient than
, is more efficient than 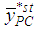 if
if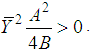
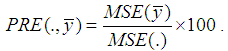
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
