| [1] | Cochran, W.G. The estimation of the yields of the cereal experiments by sampling for the Ratio of grain to total produce, Jour. Agri. Sci. 59, 1225-1226. |
| [2] | Robson, D.S. Applicationf multivariate polykays to the theory of unbiased ratio type estimation. J.Amer.stat. Assoc.,52, 411-422. |
| [3] | Upadhyaya, L.N. and Singh, H.P. Use of transformed auxiliary variable in estimating the finite population mean, Biometrical Journal 41 (5), 627-636. |
| [4] | Singh, G.N. On the improvement of product method of estimation in sample surveys. JISAS, 56, 267-275. |
| [5] | Singh, H.P. and Tailor, R. Use of known correlation co-efficient in estimating the finite population means, Statistics in Transition 6 (4), 555-560. |
| [6] | Singh, H.P., Tailor, R., Tailor, R. and Kakran, M.S. (2004): An improved estimator of population mean using power transformation, Journal of the Indian Society of Agricultural Statistics 58(2), 223-230. |
| [7] | Singh, H.P., Tailor, R. Singh, S. and Kim, J. M. A modified estimator of population mean using power transformation. Statistical Papers, 49, 37-58. |
| [8] | Singh, H.P., Tailor, R., and Tailor, R. (2010). On ratio and product methods with certain known population parameters of auxiliary variable in sample surveys. SORT, 34, 2,157-180. |
| [9] | Singh, H.P., Tailor, R., Tailor, R. and Kakran, M.S. An improved estimator of population mean using power transformation, Journal of the Indian Society of Agricultural Statistics 58(2), 223-230. |
| [10] | Kadilar, C. and Cingi, H. Ratio estimators in simple random sampling, Applied Mathematics and Computation 151, 893-902. |
| [11] | Kadilar, C. and Cingi, H. An improvement in estimating the population mean by using the correlation co-efficient, Hacettepe Journal of Mathematics and Statistics Volume 35 (1), 103-109. |
| [12] | Tailor, R. and Sharma B.K. (2009). A modified ratio-cum-product estimator of finite population mean using known coefficient of variation and coefficient of kurtosis. Statistics in Transition-New series, 10, 1, 15—24. |
| [13] | Yan, Z. and Tian, B. (2010): Ratio method to the mean estimation using co-efficient of skewness of auxiliary variable, ICICA , Part II, CCIS 106, pp. 103–110. |
| [14] | Yadav S.K. Efficient estimators for population variance using auxiliary information. Global Journal of Mathematical Sciences: Theory and Practical 3:369-376. |
| [15] | Pandey H, Yadav S K, Shukla A.K. An improved general class of estimators estimating population mean using auxiliary information. International Journal of Statistics and Systems 6:1-7. |
| [16] | Subramani, J. and Kumarapandiyan, G. (2012): Estimation of Population Mean Using Co-Efficient of Variation and Median of an Auxiliary Variable. International Journal of Probability and Statistics 1(4): 111-118. |
| [17] | Solanki RS, Singh HP, Rathour A. An alternative estimator for estimating the finite population mean using auxiliary information in sample surveys. International Scholarly Research Network: Probability and Statistics, 2012:1-14. |
| [18] | Onyeka AC (2012) Estimation of population mean in poststratified sampling using known value of some population parameter(s). Statistics in Transition-New Series 13:65-78. |
| [19] | Jeelani, M.I., Maqbool, S. and Mir, S.A. Modified Ratio Estimators of Population Mean Using Linear Combination of Co-efficient of Skewness and Quartile Deviation. International Journal of Modern Mathematical Sciences, 6, 3, 174-183. |
| [20] | Yadav, S.K. and Kadilar, C. (2013): Improved class of ratio and product estimators, Applied Mathematics and Computation, 219, 10726–10731. |
| [21] | Tailor, R., Chouhan, S. and Kim, J-M. Ratio and Product Type Exponential Estimators of Population Mean in Double Sampling for Stratification, Communications for Statistical Applications and Methods, 21, 1, 1-9. |
| [22] | Hansen, M. H., Hurwitz, W. N. and Gurney, M. Problems and methods of the sample survey of business, Journal of the American Statistical Association, 41, 173–189. |
| [23] | Ige, A. F. and Tripathi, T. P. On doubling for stratification and use of auxiliary information, J. Ind. soc. Agricul. statist., 39, p. 191-201. |
| [24] | R. Singh, P. Chauhan, N. Sawan, On linear combination of Ratio-product type exponential estimator for estimating finite population mean, Statistics in Transition,9(1),105-115. |
| [25] | S. Bahl and R.K Tuteja, Ratio and product type exponential estimator, Information and optimization Sciences, XII (I), 159-163. |
| [26] | Prasad, B. (1989): Some improved ratio type estimators of population mean and ratio in finite population sample surveys, Communications in Statistics: Theory and Methods 18, 379–392. |
| [27] | Gujrati, D.N. Basic Econometrics, Fourth Edition, McGraw-Hill. |

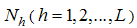 with
with 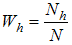 as strata weights. When these strata weights are not known, two phase sampling scheme for stratification is used. Following procedure has been followed for two phase sampling scheme for stratification as given by Tailor et.al [21],(1) A sample of size
as strata weights. When these strata weights are not known, two phase sampling scheme for stratification is used. Following procedure has been followed for two phase sampling scheme for stratification as given by Tailor et.al [21],(1) A sample of size 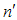 is drawn at first phase using simple random sampling without replacement technique and the observations are taken on auxiliary variable X only.(2) This sample of size
is drawn at first phase using simple random sampling without replacement technique and the observations are taken on auxiliary variable X only.(2) This sample of size 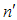 is stratified into L strata based on auxiliary variable. Let
is stratified into L strata based on auxiliary variable. Let 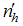 be the number of units in hth stratum
be the number of units in hth stratum 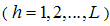 such that
such that 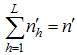 .(3) From these
.(3) From these 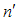 units, a sample of size
units, a sample of size 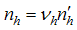 is drawn, where
is drawn, where 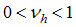 is the predetermined probability of selecting a sample of size
is the predetermined probability of selecting a sample of size 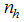 from strata of size
from strata of size 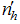 and it constitutes a sample of size
and it constitutes a sample of size 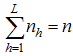 . From this sample observations on both the variables Y and X are taken.Following notations have been used in this manuscript,
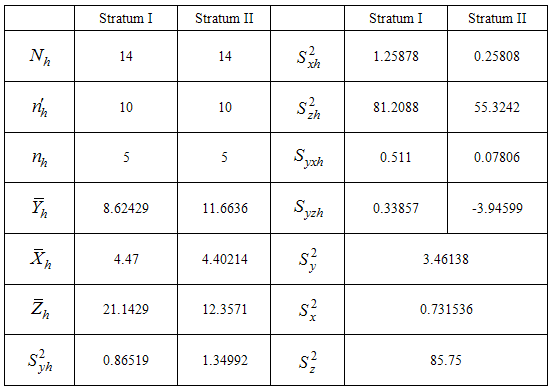
. From this sample observations on both the variables Y and X are taken.Following notations have been used in this manuscript,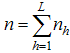 - Size of the sample at second phase
- Size of the sample at second phase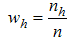 - hth stratum weight for the second phase sample
- hth stratum weight for the second phase sample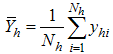 - hth stratum mean for the study variable Y
- hth stratum mean for the study variable Y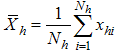 - hth stratum mean for the auxiliary variable X
- hth stratum mean for the auxiliary variable X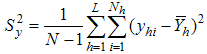 - Population mean square deviation for the study variable Y
- Population mean square deviation for the study variable Y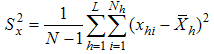 - Population mean square deviation for the auxiliary variable X
- Population mean square deviation for the auxiliary variable X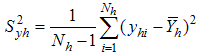 - hth stratum mean square deviation for the study variable Y
- hth stratum mean square deviation for the study variable Y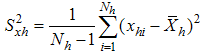 - hth stratum mean square deviation for the auxiliary variable X
- hth stratum mean square deviation for the auxiliary variable X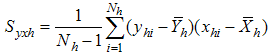 - Covariance between y and x in hth stratum
- Covariance between y and x in hth stratum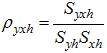 - Correlation coefficient between y and x in the hth stratum
- Correlation coefficient between y and x in the hth stratum 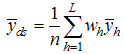 - Unbiased estimator of population mean
- Unbiased estimator of population mean 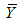 in second phase sampling
in second phase sampling 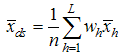 - Unbiased estimator of population mean in second phase sampling
- Unbiased estimator of population mean in second phase sampling 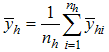 - hth stratum mean at second phase sampling for the study variable Y
- hth stratum mean at second phase sampling for the study variable Y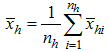 - hth stratum mean at second phase sampling for the auxiliary variable X
- hth stratum mean at second phase sampling for the auxiliary variable X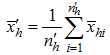 - hth stratum mean at first phase sampling for the auxiliary variable X
- hth stratum mean at first phase sampling for the auxiliary variable X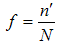 - First phase sampling fractionHansen et.al [22] proposed the classical combined ratio estimator for population mean under stratified random sampling as,
- First phase sampling fractionHansen et.al [22] proposed the classical combined ratio estimator for population mean under stratified random sampling as,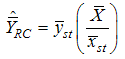
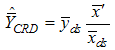
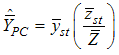
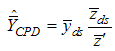
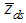 ,
, 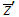 have their usual meanings.The biases and mean square errors of the estimators in (1.2) and (1.4) respectively are,
have their usual meanings.The biases and mean square errors of the estimators in (1.2) and (1.4) respectively are,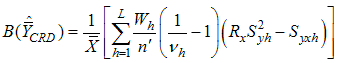
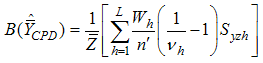
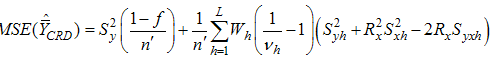
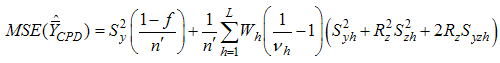
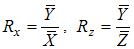 and
and 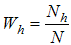 .Singh et.al [24] suggested following exponential ratio and product type estimators in stratified random sampling based on Bahl and Tuteja [25] estimators of population mean under simple random sampling as,
.Singh et.al [24] suggested following exponential ratio and product type estimators in stratified random sampling based on Bahl and Tuteja [25] estimators of population mean under simple random sampling as,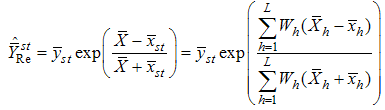
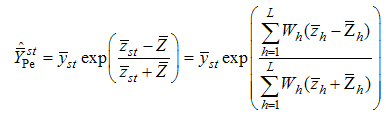
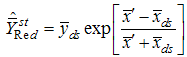
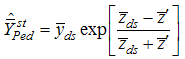
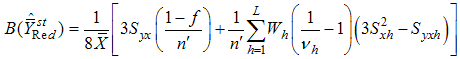
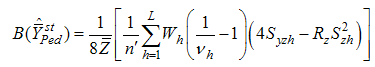
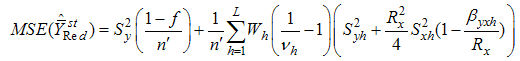
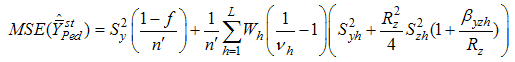
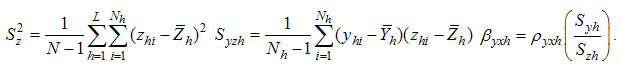
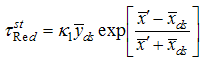
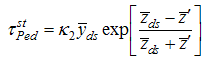
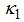 and
and 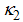 are suitably chosen constant to be determined such that the mean square errors of the estimators (3.1) and (3.2) are minimum respectively.To study the large sample properties of the proposed estimators, we define
are suitably chosen constant to be determined such that the mean square errors of the estimators (3.1) and (3.2) are minimum respectively.To study the large sample properties of the proposed estimators, we define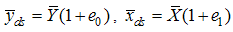 and
and 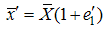 such that
such that 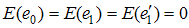 and
and 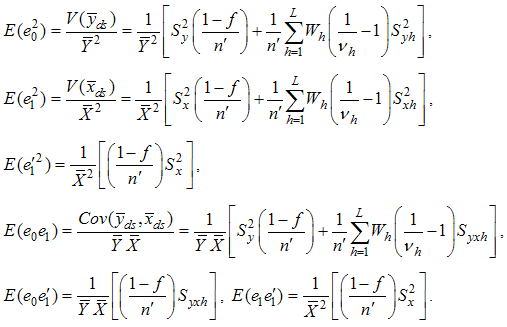 Expressing
Expressing  in terms of
in terms of  , we have
, we have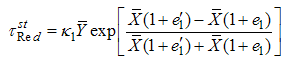 On simplification, we have
On simplification, we have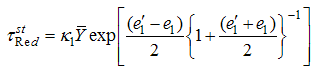 After expansion and simplification, we get
After expansion and simplification, we get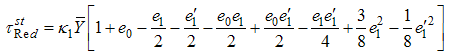
 from both the sides and taking expectation both sides, we get bias of
from both the sides and taking expectation both sides, we get bias of  as,
as,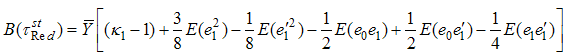
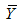 from both the of (3.3), squaring and simplifying up to the first order of approximation we have,
from both the of (3.3), squaring and simplifying up to the first order of approximation we have,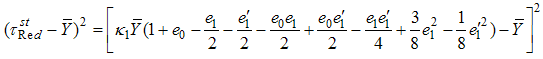 Expanding, simplifying and taking expectations on both the sides, we get the mean square error of
Expanding, simplifying and taking expectations on both the sides, we get the mean square error of 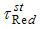 , up to the first order of approximation as,
, up to the first order of approximation as,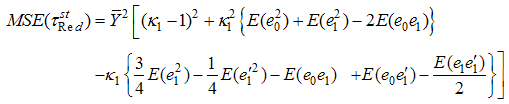
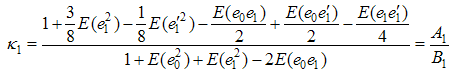
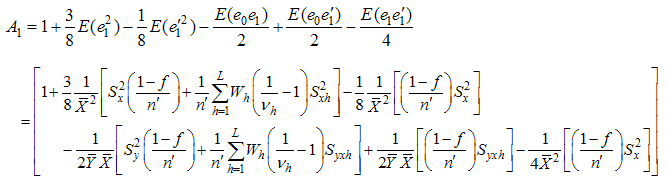
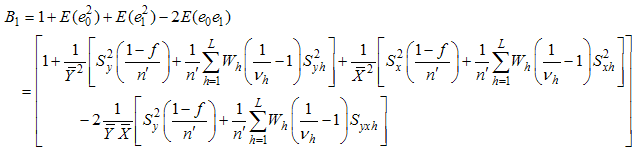 And the minimum mean square error is,
And the minimum mean square error is,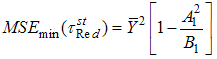
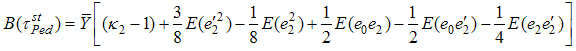
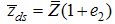 and
and 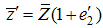 such that
such that 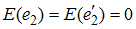 and
and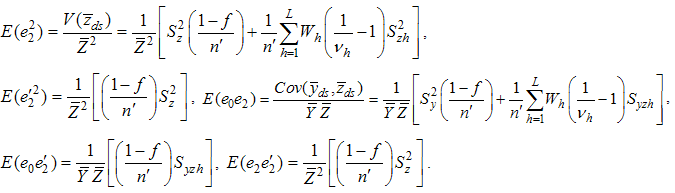
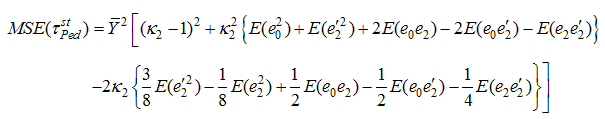
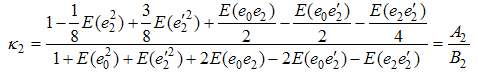
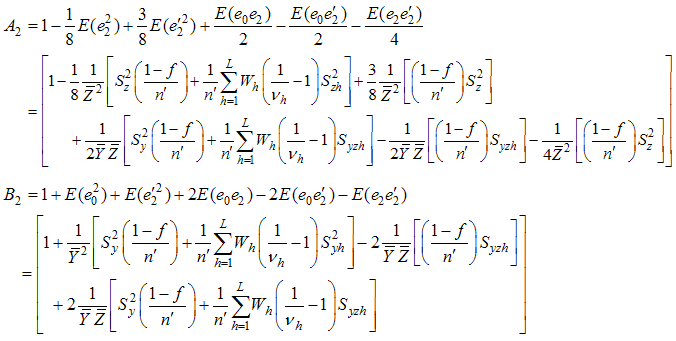 And the minimum mean square error is,
And the minimum mean square error is,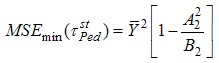
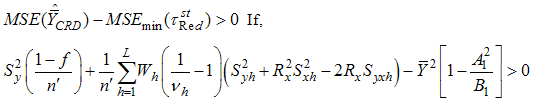
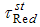 is better than the estimator
is better than the estimator 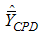 if
if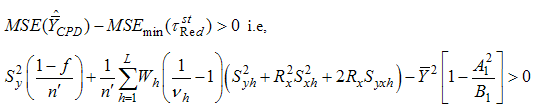
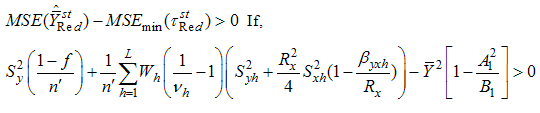
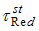 is better than the estimator
is better than the estimator 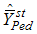 if
if 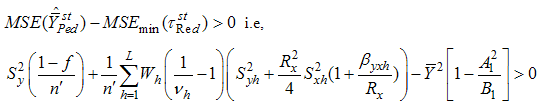
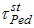 .
.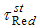 and
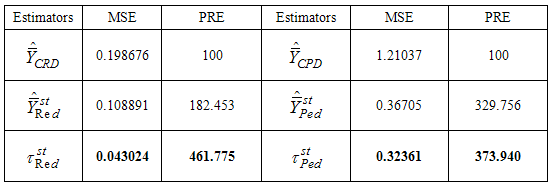
and 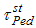 have lesser mean square errors than the other mentioned estimators of population mean under two phase sampling for stratification. It means the estimated values of the parameter (population mean) by these estimators are very close to the actual value of the parameter. The main aim of the study is to find the estimators which predict the values very close to the actual value of the parameter with minimum mean squared error. Here in the present study the major goal is obtained as the proposed estimators have the minimum mean square errors. Thus we infer that the proposed estimators should be preferred for the estimation of population mean in two phase sampling for stratification.
have lesser mean square errors than the other mentioned estimators of population mean under two phase sampling for stratification. It means the estimated values of the parameter (population mean) by these estimators are very close to the actual value of the parameter. The main aim of the study is to find the estimators which predict the values very close to the actual value of the parameter with minimum mean squared error. Here in the present study the major goal is obtained as the proposed estimators have the minimum mean square errors. Thus we infer that the proposed estimators should be preferred for the estimation of population mean in two phase sampling for stratification.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML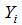 (Thousands of wildcats),
(Thousands of wildcats), 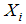 (per barrel price),
(per barrel price), 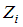 (time)
(time)