1. Introduction

Queueing with customer impatience has vast applications in computer-communications, bio-medical modelling, service systems etc. It is important to note that the prevalence of the phenomenon of customer impatience has adverse effect on the system’s performance. If we talk from business point of view, the firms lose their potential customers due to customer impatience which affects the business of the firms as a whole. If the firms employ certain customer retention strategies then there are chances that a certain fraction of impatient customers can be retained in the queueing system. An impatient customer (due to reneging) may convinced to stay in service system for his service by utilizing certain convincing mechanisms. Such customers are termed as retained customers. When a customer gets impatient, he may leave the queue with some probability, say 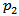and may remain in the queue for service with some complementary probability .

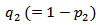Feedback in queueing literature represents customer dissatisfaction because of inappropriate quality of service. In case of feedback, after getting partial or incomplete service, customer retries for service. In computer communication, the transmission of protocol data unit is sometimes repeated due to occurrence of an error. This usually happens because of non-satisfactory quality of service. Rework in industrial operations is also an example of queues with feedback. We assume that after the completion of service, each customer may rejoin the system as a feedback customer for receiving another regular service with probability p₁ and may not join with complementary probability 1- p₁.

Queues with discouraged arrivals have applications in computers with batch job processing where job submissions are discouraged when the system is used frequently and arrivals are modelled as a Poisson process with state dependent arrival rate. The discouragement affects the arrival rate to the queueing system. Customers arrive in a Poisson fashion with rate that depends on the number of customers present in the system at that time i.e. .

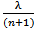Taking these concepts into consideration, a single-server, finite capacity, Markovian feedback queueing model with discouraged arrivals, reneging, and retention of reneged customers is studied. The steady-state solution of the model is derived.

Rest of the paper is structured as follows: In section 2, the literature review is presented. In section 3, queueing model is formulated. The differential-difference equations are derived and solved iteratively in section 4. Measures of effectiveness are derived in section 5. Some queuing models are derived as special cases of this model in section 6. The conclusions are presented in section 7.

2. Literature Survey

Customer impatience has become the burning problem of private as well as government sector enterprises. Queue with reneging is firstly studied by Haight [6]. He studies the problem like how to make rational decisions while waiting in the queue, the probable effect of this decision etc. Ancker and Gafarian [1] study queuing system with balking and reneging, and perform its steady state analysis. Ancker and Gafarian [2] also obtain results for a pure balking system (no reneging) by setting the reneging parameter equal to zero. Multi-server queuing systems with customer impatience find their applications in many real life situations such as in hospitals, computer-communication, retail stores etc. Kapodistria [7] study a single server Markovian queue with impatient customers and considered the situations where customers abandon the system simultaneously. She considers two abandonment scenarios. In the first one, all present customers become impatient and perform synchronized abandonments, while in the second scenario; the customer in service is excluded from the abandonment procedure. She extends this analysis to the M/M/c queue under the second abandonment scenario also. Kumar [8] investigates a correlated queuing problem with catastrophic and restorative effects with impatient customers which have special applications in agile broadband communication networks. Kumar and Sharma [9] study an M/M/1/N queuing model with balking, reneging and retention of reneged customers which has applications in supply chain management. They also perform the cost-profit analysis of the model.

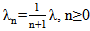Queueing models where potential customers are discouraged by queue length are studied by many researchers. Natvig [12] studies the single server birth-death queueing Procea2wv bnss with state-dependent parameters and 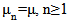. He reviews state dependent queueing models of different kind and compare his results with M/M/1, M/D/1 and D/M/1 and the single server birth-and-death queueing model with parameters 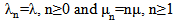numerically. Von Doorn [18] obtains exact expressions for transient state probabilities of the birth death process with parameters 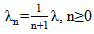and 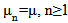. Ammer et al. [3] study single server, finite capacity, Markovian queue with discouraged arrivals and reneging using matrix method.

Takacs [16] studies queue with feedback to determine the stationary process for the queue size and the first two moments of the distribution function of the total time spent in the system by a customer. Davignon and Disney [5] study single server queues with state dependent feedback. Santhakumaran and Thangaraj [13] consider a single server feedback queue with impatient and feedback customers. They study M/M/1 queueing model for queue length at arrival epochs and obtain result for stationary distribution, mean and variance of queue length. Thangaraj and Vanitha [17] obtain transient solution of M/M/1 feedback queue with catastrophes using continued fractions. The steady-state solution, moments under steady state and busy period analysis are calculated. Ayyappan et al. [4] study M/M/1 retrial queueing system with loss and feedback under non-pre-emptive priority service by matrix geometric method.

Kumar and Sharma [10] study the retention of reneged customers in an M/M/1/N queuing model and perform the sensitivity analysis. They further study M/M/1/N queuing system with retention of reneged customers and balking, refer [11]. Sharma and Kumar [14, 15] study some Markovian queuing systems with feedback and retention of impatient customers. Bouchentouf and Belarbi [20] study some retrial queueing models with balking and feedback. Recently, Kumar and Sharma [19] study a two heterogeneous servers queueing model with reneging, discouragement and retention of reneged customers. They perform the steady-state analysis of the model.

3. Queuing Model Formulation

We consider a single-server queuing system in which the customers arrive in a Poisson fashion with rate that depends on the number of customers present in the system at that time i.e. 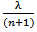and the average service rate is µ. After completion of each service, the customer can either join at the end of the queue with probability p₁ or he can leave the system with probability q₁, where p₁+q₁ = 1. The probability distributions of inter-arrival and service times are taken as exponential as most of the real life situation fit well to this distribution. The capacity of the system is taken as finite, say N. There is a single server. The customers both newly arrived and those that are fed back are served in order in which they join the tail of original queue. The queue discipline is FCFS. We do not distinguish between the regular arrival and feedback arrival. Each customer upon arriving in the queue will wait a certain length of time for his service to begin. If it has not begun by then, he will get impatient and may leave the queue without getting service with probability 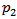and may remain in the queue for his service with probability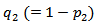. The reneging times follow exponential distribution with parameter .

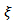4. Differential-Difference Equations and Solution of the Queuing Model

Let 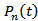be the probability that there are n customers in the system at time t.

The differential-difference equations are derived by using the general birth-death arguments. These equations are solved iteratively in steady-state in order to obtain the steady-state solution.

The differential-difference equations of the model are:

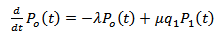(1)

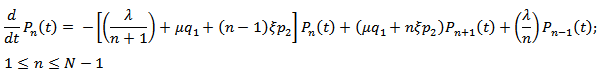(2)

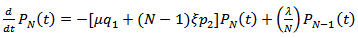(3)

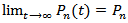In steady state, and therefore, 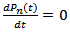as 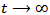and hence, the equations (1) to (3) gives the difference equations

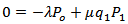(4)

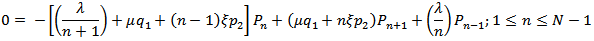(5)

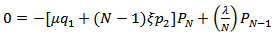(6)

Solving iteratively equations (4) – (6), we get

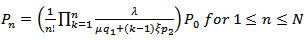(7)

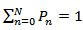Using the normalization condition, , we get

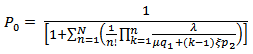(8)

Hence, the steady-state probabilities of the system size are derived explicitly.

5. Measure of Effectiveness

In this section, some important measures of effectiveness are derived. These can be used to study the performance of the queuing system under consideration.

5.1. The Expected System Size (L_s)

The expected system size provides the average number of customers in the system. This can be computed by using the formula given below.

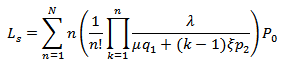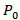Where is given in (8).

5.2. The Expected Queue Length (L_q)

The average queue length is given by;

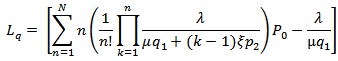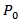Where is given in (8) and all other parameters are discussed in the previous sections.

5.3. The Expected Waiting Time in the System (W_s)

The average waiting time of a customer in the system is derived as:

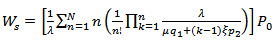
5.4. The Expected Waiting Time in the Queue (W_q)

The average waiting time of a customer in the system is derived as:

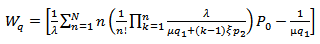
5.5. Rate of Abandonment,

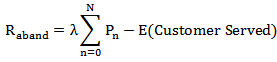
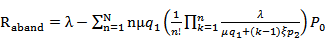
5.6. Expected Number of Waiting Customers, Who Actually Wait, E (Customer Waiting)

Average number of customers who actually wait is given by the following formula.

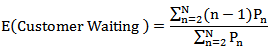
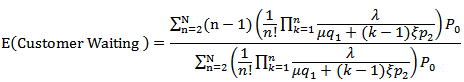
5.7. Probability Distribution of Busy Period, Prob (Busy Period)

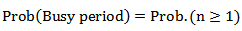
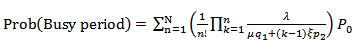where 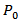has been computed in (8).

6. Special Cases

In this section we derive some derive important queueing models as special cases of this model.

6.1. When there is no Retention of Reneged Customers (i.e. q₂ = 0)

The queuing system reduces to a single server Markovian feedback queuing system with discouraged arrivals and reneging with

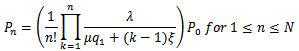Using the normalization condition, 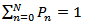, we get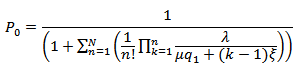

6.2. When There is No Discouragement

The model reduces to an M / M /1 / N feedback queuing system with retention of reneged customers as studied by Sharma and Kumar [14] with

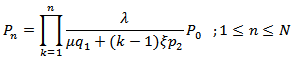Using the normalization condition, 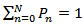, we get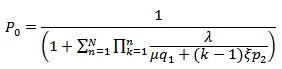

6.3. When there is no Feedback (i.e. q₁ = 1)

The queuing system reduces to a single server Markovian queuing system with discouraged arrivals and retention of reneged customers with

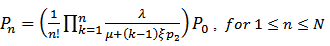Using the normalization condition, 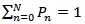, we get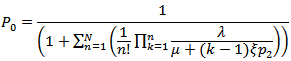

6.4. When there is no Feedback (i.e. q₁ = 1) and no Discouragement

The model reduces to an M / M /1 / N queuing system with retention of reneged customers as studied by Kumar and Sharma [10] with

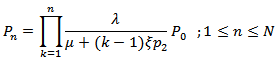Using the normalization condition, 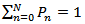, we get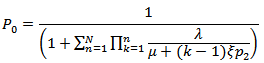

7. Conclusions and Future Work

This paper studies a single server Markovian feedback queuing model with discouraged arrivals, reneging, and retention of reneged customers. We obtain the steady-state solution and different measures of effectiveness. Some queuing models are derived as special cases of this model. This model finds its applications in businesses and industries facing the problems of customers impatience and dissatisfaction in service.

The model analysis is limited to finite capacity. The infinite capacity case of the model can also be studied. Further, the model can be solved in transient state to get time-dependent results. The cost-profit analysis of the model can also be carried to study its economic aspects. The same idea can be extended to non-Markovian queuing models.