N. K. Jain1, Rakesh Kumar2, Bhupender Kumar Som1
1Department of Statistics and Operational Research, Kurukshetra University, Kurukshetra - 136119 (India)
2School of Mathematics, Shri Mata Vaishno Devi University, Sub Post-Office, Katra – 182320 (India)
Correspondence to: Rakesh Kumar, School of Mathematics, Shri Mata Vaishno Devi University, Sub Post-Office, Katra – 182320 (India).
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we develop and introduce the concept of reverse balking in a single server Markovian queuing system having finite capacity. The concept of reverse balking evolves from its application in investment business. In such business, more number of customers associated with a firm becomes the attracting factor for investing customers and conversely. The steady-state solution of the model is obtained and different measures of effectiveness are derived. Sensitivity analysis of the model is also performed.
Keywords:
Reverse Balking, Queuing Model, Steady-State Solution, Sensitivity analysis, Finite capacity
Cite this paper: N. K. Jain, Rakesh Kumar, Bhupender Kumar Som, An M/M/1/N Queuing System with Reverse Balking, American Journal of Operational Research, Vol. 4 No. 2, 2014, pp. 17-20. doi: 10.5923/j.ajor.20140402.01.
1. Introduction
In this era of globalization and liberalization managing business has become a challenging task. Customers have become more selective. Brand switching is more frequent. Customer impatience has become a burning problem in the corporate world. Queuing theory offers various models that can be used in various service systems facing customer impatience. The notion of customer balking appears in queuing theory in the work of Haight [3]. He studies an M/M/1 queue with balking in which there is a greatest queue length at which the arrival will not balk. Ancker and Gafarian [1] study M/M/1/N queuing system with balking and reneging and derive its steady-state solution. Ancker and Gafarian [2] obtain results for a pure balking system by setting the reneging parameter equal to zero. Rao [5] studies a queuing process of M/G/1 type where the customers balk as well as renege. In the abovementioned queuing models reneging and balking are the functions of either system size or queue length. Larger is the system size more is balking and similar is the case of reneging. But when it comes to the sensitive businesses like investment, customers invest with the firms having large number of customers (investors) with them. Thus, the probability of joining of customers in such firms is high. Therefore in the businesses like customer investment, the probability of balking will be low when the system size is more and vice-versa, which is the balking in reverse sense (called as Reverse Balking).For example, in case of life insurance business where the purchase of a policy refers to the arrival of a customer into the queuing system (insurance firm), the processed policy claim refers to as the departure from the queuing system, the claim processing department is considered as a single server and the system capacity (the number of policies it can accommodate) is taken as finite. The claims are processed in order of their arrival (i.e. the queue discipline is FCFS). The probability of joining (i.e. chances of purchasing a policy) the firm is more when it has more number of insured customers with it and vice-versa (reverse balking). Modeling such a system using queuing theory may help the decision makers in knowing the average number of policies with the firm and the probability of having n (=0,1,2,…,N) number of policies.In this paper, we study an M/M/1/N queuing system with reverse balking. We present the steady-state analysis and derive some important measures of performance. Rest of the paper is arranged as follows: In section 2, the model is described. In section 3, mathematical formulation of the model is presented. In section 4, steady-state solution of the model is obtained and some measures of performance are derived. Sensitivity analysis of the model is presented in section 5 of the paper. Section 7 deals with the conclusion.
2. Description of the Model
The queuing model considered in this paper is based on following assumptions:1) The arrivals (purchase of insurance policies) to a queuing system (insurance firm) occur one by one in accordance with a Poisson process with mean rate . The inter-arrival times are independently, identically and exponentially distributed with parameter.2) There is a single-server (claim processing department) and the customers are served (policy claims are processed) one by one. The service (claim processing) times are independently, identically and exponentially distributed with parameter .3) The capacity of the system (the total number of policies the insurance firm can accommodate) is finite, say N.4) The policy claims are processed in order of their arrival, i.e. the queue discipline is First-Come, First-Served.5) (a) When the system is empty (in the case of new insurance business) customers may balk (do not purchase policy) with probability 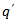 and may enter (may purchase the policy) with probability
and may enter (may purchase the policy) with probability 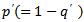 . (b) When there is at least one customer (policy holder) in the system, the customers balk with a probability
. (b) When there is at least one customer (policy holder) in the system, the customers balk with a probability 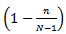 and join the system with probability
and join the system with probability 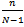 .
.
3. Mathematical Formulation of the Model
In this section we present mathematical model of the system. We define,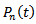 = the probability that there are n customers in the system at time t.The differential-difference equations of the model are derived by using general birth-death arguments:
= the probability that there are n customers in the system at time t.The differential-difference equations of the model are derived by using general birth-death arguments: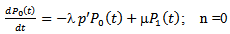 | (1) |
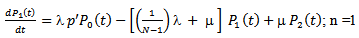 | (2) |
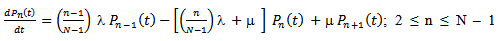 | (3) |
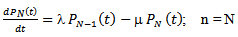 | (4) |
4. Steady-State Solution
In this section, we present the steady-state solution of the model. In steady-state, 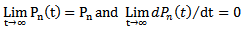 Therefore, the equations (1) to (4) become
Therefore, the equations (1) to (4) become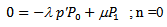 | (5) |
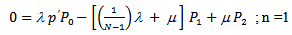 | (6) |
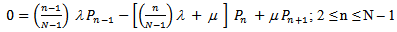 | (7) |
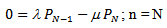 | (8) |
The equations (5) to (8) are solved iteratively to obtainTo determine 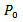 we use the condition of normality
we use the condition of normality 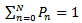
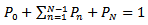
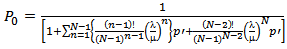 | (10) |
Measures of PerformanceIn this sub-section we present some important measures of performance. One can study the long run performance of any system using these measures.(i) Expected System Size (Average number of insurance policies with a firm), 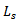 :
: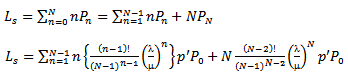 | (11) |
Using (11) one can compute an average number of policies with any insurance firm in long run.Using Little’s Law, 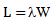 other measures can be derived as under:(ii) Expected Waiting Time of a customer in the System is given by,
other measures can be derived as under:(ii) Expected Waiting Time of a customer in the System is given by, 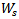 :
: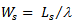 where
where 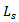 is given in (11) and
is given in (11) and 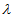 is the mean arrival rate.(iii) Expected Waiting Time of a customer in the queue,
is the mean arrival rate.(iii) Expected Waiting Time of a customer in the queue, 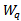 :
: 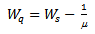 where
where 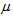 is the mean service rate.(iv) Expected Queue Length,
is the mean service rate.(iv) Expected Queue Length, 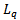
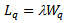
5. Sensitivity Analysis
In this section, we present sensitivity analysis of the model. We study variations in expected system size (Ls) with respect to the probability of balking (q’), the mean arrival rate 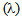 and the mean service rate
and the mean service rate 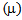 . In fig.-1, the variation in expected system size, Ls with respect to the probability of balking (q’) (when the system is empty) is shown. We can see that the expected system size is zero when
. In fig.-1, the variation in expected system size, Ls with respect to the probability of balking (q’) (when the system is empty) is shown. We can see that the expected system size is zero when 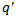 is 1, i.e. there is no arrival to the system. It increases regularly with the decrease in
is 1, i.e. there is no arrival to the system. It increases regularly with the decrease in  and attains maximum value when
and attains maximum value when  is zero. Thus, one can foresee the status of expected system size with given values of parameters with the help of fig-1.
is zero. Thus, one can foresee the status of expected system size with given values of parameters with the help of fig-1. | Figure 1. Here λ = 2, μ = 3, N = 5 |
Fig.-2 depicts the variation in expected system size, Ls with respect to mean arrival rate, 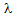 . There is a proportionate increase in Ls with the increase in
. There is a proportionate increase in Ls with the increase in 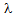 for the given values of system parameters. The reason is obvious. The arrival rate increases and service rate remains constant, therefore the average number of customers in the system increases.
for the given values of system parameters. The reason is obvious. The arrival rate increases and service rate remains constant, therefore the average number of customers in the system increases. 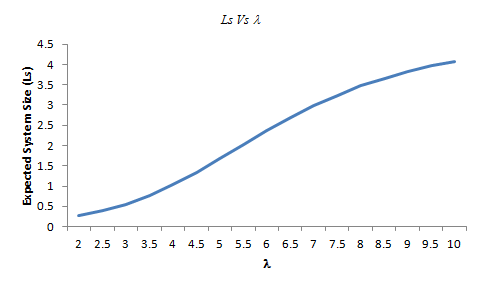 | Figure 2. Here μ = 3, q′ = 0.8, N = 5 |
If we see fig.-3, the expected system size decreases regularly with the increase in mean service rate 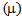 . The reason is that the arrival rate remains constant and the service rate increases.Thus, by performing such sensitivity analysis one can study and know functioning of his business under the reverse balking.
. The reason is that the arrival rate remains constant and the service rate increases.Thus, by performing such sensitivity analysis one can study and know functioning of his business under the reverse balking.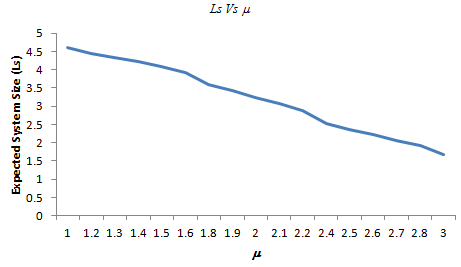 | Figure 3. Here λ = 2, q′ = 0.8, N = 5 |
6. Conclusions
In this paper, we develop and incorporate the concept of reverse balking into an M/M/1/N queuing system. An application of this model in insurance business is discussed. We obtain the steady-state solution of the model. We also derive some important performance measures and perform sensitivity analysis of the model. The model studied in this paper can also be applied in various segments of investment business like insurance, mutual funds, banking sector, telecommunication sector, automobile sector, and health care etc.
References
| [1] | Ancker Jr., C. J. and Gafarian, A.V., “Some queuing problems with balking and reneging I”, Operations Research, vol. 11, no. 1, pp. 88–100, 1963. |
| [2] | Ancker Jr., C. J. and Gafarian, A.V., “Some queuing problems with balking and reneging II”, Operations Research, vol. 11, no. 6, pp. 928–937, 1963. |
| [3] | Haight, F. A., “Queuing with balking”, Biometrika, vol. 44, no. 3-4, pp. 360-369, 1957. |
| [4] | Haight, F. A., “Queuing with reneging”, Metrika, vol. 2, no.1, pp. 186-197, 1959. |
| [5] | Rao, S. S., “Queuing models with balking, reneging and interruptions”, Operations Research, vol. 13, no. 4, pp. 596-608, 1965. |

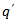 and may enter (may purchase the policy) with probability
and may enter (may purchase the policy) with probability 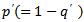 . (b) When there is at least one customer (policy holder) in the system, the customers balk with a probability
. (b) When there is at least one customer (policy holder) in the system, the customers balk with a probability 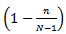 and join the system with probability
and join the system with probability 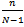 .
.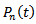 = the probability that there are n customers in the system at time t.The differential-difference equations of the model are derived by using general birth-death arguments:
= the probability that there are n customers in the system at time t.The differential-difference equations of the model are derived by using general birth-death arguments: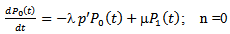
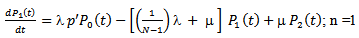
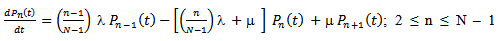
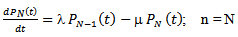
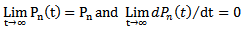 Therefore, the equations (1) to (4) become
Therefore, the equations (1) to (4) become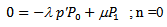
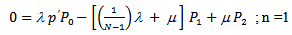
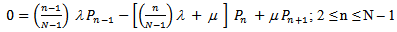
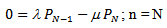
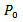 we use the condition of normality
we use the condition of normality 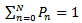
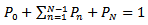
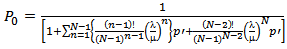
 :
: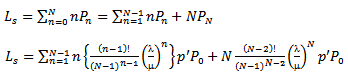
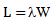 other measures can be derived as under:(ii) Expected Waiting Time of a customer in the System is given by,
other measures can be derived as under:(ii) Expected Waiting Time of a customer in the System is given by, 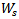 :
: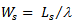 where
where 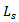 is given in (11) and
is given in (11) and 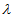 is the mean arrival rate.(iii) Expected Waiting Time of a customer in the queue,
is the mean arrival rate.(iii) Expected Waiting Time of a customer in the queue, 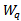 :
: 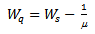 where
where 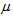 is the mean service rate.(iv) Expected Queue Length,
is the mean service rate.(iv) Expected Queue Length, 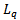
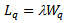
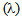 and the mean service rate
and the mean service rate 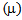 . In fig.-1, the variation in expected system size, Ls with respect to the probability of balking (q’) (when the system is empty) is shown. We can see that the expected system size is zero when
. In fig.-1, the variation in expected system size, Ls with respect to the probability of balking (q’) (when the system is empty) is shown. We can see that the expected system size is zero when 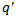 is 1, i.e. there is no arrival to the system. It increases regularly with the decrease in
is 1, i.e. there is no arrival to the system. It increases regularly with the decrease in 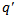 and attains maximum value when
and attains maximum value when 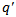 is zero. Thus, one can foresee the status of expected system size with given values of parameters with the help of fig-1.
is zero. Thus, one can foresee the status of expected system size with given values of parameters with the help of fig-1.
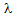 . There is a proportionate increase in Ls with the increase in
. There is a proportionate increase in Ls with the increase in 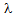 for the given values of system parameters. The reason is obvious. The arrival rate increases and service rate remains constant, therefore the average number of customers in the system increases.
for the given values of system parameters. The reason is obvious. The arrival rate increases and service rate remains constant, therefore the average number of customers in the system increases. 
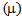 . The reason is that the arrival rate remains constant and the service rate increases.Thus, by performing such sensitivity analysis one can study and know functioning of his business under the reverse balking.
. The reason is that the arrival rate remains constant and the service rate increases.Thus, by performing such sensitivity analysis one can study and know functioning of his business under the reverse balking.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML