1. Introduction

Until the middle of the 1970s, GP applications reported in the literature were rather scarce. Since that time, and chiefly due to seminal works by Lee[1] and Ignizio[2], an impressive boom of GP applications and technical improvements have arisen. It has been applied successfully in practice for many years. However, determining precise aspiration levels for the objectives in real world problems often is a difficult task for decision maker(s) Zeleny[3], and Yaghoobi and Tamiz[4]. In fact, there are many decision making situations where the DM does not have complete information of some parameters and, in particular, the goals values in the GP model Aouni et al.[5].

One of the main approaches for considering impreciseness in decision making is fuzzy goal programming. The use of membership functions in the GP based on the Fuzzy Set Theory was first carried out by Zimmermann[6], Narasimhan[7], further extensions were provided by Hannan [8], Tiwari et al.[9], Chen and Tsai[10], Yaghoobi and Tamiz [4].

The majority of FGP formulations and applications are based on the model developed by Hannan[8]. A different approach is proposed by Tiwari et al.[9]. Based on piecewise linear approximation (PLA), Yang et al.[11] have further formulated the problem with fewer variables, which can lead the same solutions as Narasimhan’s and Hannan’s model. Kim and Whang[12] have proposed an FGP formulation where the concept of tolerances is introduced to express the fuzzy goals of the DM instead of using the conventional membership functions. Chen and Tsai[10], and Chen and Weng[13] have suggested an extension of the additive model to consider goals of different importance and preemptive priorities, where relative importance of goals are modelled by corresponding desirable achievement degrees. Recently, Yaghoobi and Tamiz[4] have proposed a more efficient formulation and they have highlighted the fact that Kim and Whang[12] model is different to Hannan[8] model.

In the reviewed models, mostly classical structure is used and the general structure of goal programming models, including crisp and fuzzy ones, remained unchanged. However, in the real world problems, there may exist situations where the decision maker is interested in setting multi aspiration levels for each goal. The classical models of decision making including GP and FGP cannot be applied directly. To solve this type of problems, it is essential to develop new decision making models. To do this, Chang[14], has recently proposed a new method called multi-choice goal programming (MCGP) for multi-objective decision problems, which allows DMs to set multi-choice aspiration levels (MCAL) for each goal (that is to say, one goal mapping multiple targets) to avert underestimation of decision making. He revised his approach to make it easier for understanding and implementation of linear programming packages Chang[15]. Also, Ustun[16] presented the formulation of (MCGP) based on the conic scalarizing function.

The earliest MCGP formulations consider the targets as precise, deterministic, and well known. Notwithstanding, in some of the decision-making problems, it may exist situations that the decision maker could not be interested in presenting his preferred targets in a precise manner, and he does not have complete information of some parameters (i.e., the parameters can be fuzzy, imprecise, or stochastic). To deal with such situation, an additive model which is called Goal Programming with Multi Fuzzy Targets and Importance (GP-MFTI) is presented in this paper to reformulate (MCGP) in an imprecise manner by using all forms of the functions in which the concept of multi-target functions (MTFs) or fuzzy satisfaction functions (FSFs) is introduced. In other words, the indifference and veto thresholds (targets ) specified by the decision maker should be introduced in all types of the membership functions for obtaining new functions called multi-target functions (MTFs) in the sense of ( fuzzy set theory), or fuzzy satisfaction functions (FSFs) in the sense of DM’s preferences. We believe that the model developed in this paper (GP-MFTI) can be regarded as more general than MCGP formulation. Therefore, (GP MFTI) is considered as an extension of MCGP in which the DMs’ preferences are taken into account.

The rest of this article is organized as follows. In Sect. 2, multi-choice goal programming (MCGP) model is described. And, in section 3 basic structure and description of a new model (GP-MFTI) is given. A numerical example is given in Sect. 4 to illustrate the efficiency and flexibility of the presented method. Finally, we conclude this study in Sect. 5.

2. Multi-Choice Goal Programming (MCGP)

In the reviewed GP, and FGP models, the decision makers (DMs) consider one aspiration level for each goal (objective). However, in real world problems, there may exist situations where the DMs would like to make a decision on the problem, with the goal that can be achieved from some aspiration levels (i.e., one goal mapping many targets). To solve this type of problems, Chang[14, 15] has recently proposed a new method called Multi-Choice Goal Programming (MCGP). The mathematical expression of MCGP is explained in detail as follows Chang[14]:

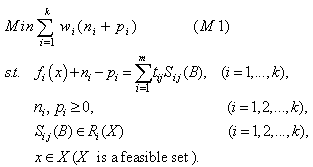where 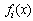is the linear function of 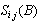represents a function of binary serial numbers that ensure only one aspiration level must be chosen in each goal, 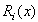is the function of resources limitations. Other variables are defined as in GP, and FGP models.

It can be seen that MCGP model is considered as an extension of GP model.

3. Goal Programming with Multi Fuzzy Targets and Importance (GP-MFTI)

In the standard MCGP formulation proposed by Chang[14, 15], and Ustun[16], the target values are assumed to be deterministic or precise, and the decision maker’s preferences are not taken into consideration, that are considered an essential element in the GP model. However, in several application situations, the manager does not have complete information of some parameters and in particular the target values (i. e. the targets of each goal can be fuzzy or imprecise). For modelling goals with imprecise nature, the authors of this paper are reformulated the standard MCGP formulation, in which the DMs have to take their preferences into account, where the concept of multi target functions (MTFs) is introduced in the new formulation. In other words, the indifference and veto thresholds (targets: 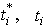) specified by the decision maker should be introduced in all types of the membership functions for obtaining new functions called multi-target functions (MTFs). The indifference, and veto thresholds concept is used for characterizing the imprecision and the preferences associated with the targets of any type of goal. The possible fuzzy multi-target goals are considered in a general form of (GP-MFTI) model as follows:

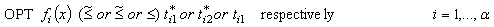(3.1)

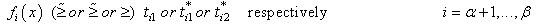(3.2)

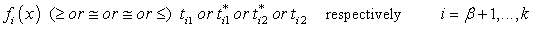(3.3)

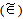where: the symbol refer to approximately belong to.

Linear multi-target functions are used in this paper to express the fuzzy multi-target goals (3.1), (3.2), and (3.3), respectively as follows:

Figure 1. Linear multi-target functions (LMTFs)

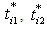In order to solve the above mentioned problem basing on the concept of deviational variables and slack variables in GP, the additive form of FGP, and MCGP techniques are used to convert (3.1)-(3.3) into (GP-MFTI) problem. For clarifying the (GP-MFTI) problem, let us consider two types of goals (3.2) and (3.3) respectively. The goal (3.3) contains four targets, , , and 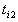in this order, such as 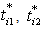, are in the first priority (indifference thresholds), and 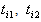, are in the second priority (veto thresholds). This is the case of FGP with an either -or selection. The target in goal (3.3) is to choose an appropriate fuzzy aspiration level from eithe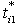r or 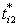or to choose an appropriate precise aspiration level from eithe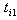r or .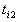

Based on the modelling of Martel and Aouni[17, 18], chang[14, 15], three extra binary variables should be added for goal (3.2), while four extra binary variables should be added to goal (3.3), in the following (GP-MFTI) model:

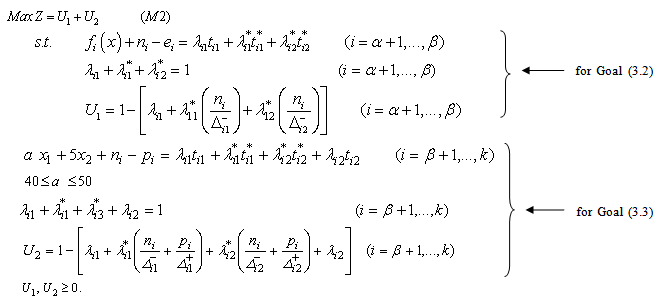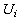where represents the multi target function or the membership function with multi-targets, which can be regarded as the achievement degrees of the fuzzy multi target goals; 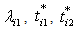, and 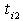are binary variables 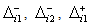and , and 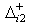are the constants of the negative and positive deviations or tolerances of the fuzzy targets of type 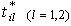from the 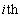goal, respectively.

The quadratic terms 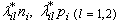can be transformed to linear form Kettani and Oral[19], Chang[14, 20].

Then the general formulation of (GP-MFTI) can be expressed of all type of multi-target goals as follows: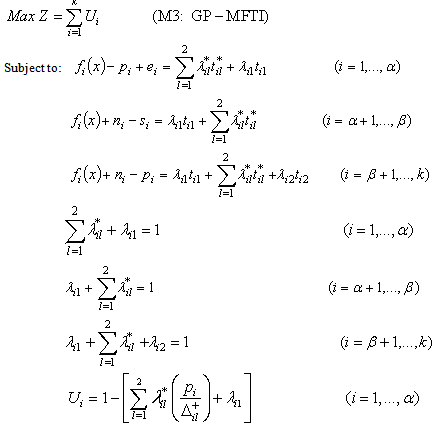

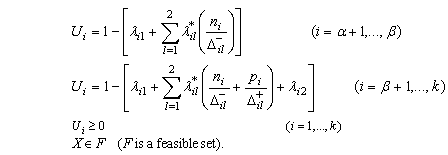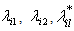where are binary variables 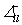and , and 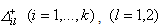are the constants of the negative and positive deviations or tolerances of the fuzzy targets of type 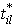from the 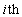goal, respectively.

Moreover, to solve the above mentioned FMTGP problems, another approach based on the Zimmermann’s formulation is proposed in this paper as follows:

It is shown that (M4) is similar to (M3).

It is shown that (GP-MFTI) model proposed by the authors is considered as an extension of MCGP with fuzzy targets in which the decision maker’s preferences are taken into consideration. In fact, the (GP-MFTI) model is based on the Multi Target Functions (MTFs) concept.

Chen and Tsai[10] made a comparison between Fuzzy additive and Fuzzy Minmax models in a numerical example; the results show that as a whole, the sum of achievement degrees in the additive model is greater than in fuzzy minmax model. This advantage makes the additive model appealing, and this model has been applied in different researchers.

Sometime in GP or FGP, the goals have different relative importance; in order to reflect the relative importance of the goals, Tiwari et al.[9] have proposed a weighted additive model that incorporates each goal’s weight into the objective function; but Chen and Tsai[10] have shown that the model may produce undesirable solutions when the weights are changed. Instead of the weighted additive model, Chen and Tsai[10] proposed a model to explicitly determine a desirable achievement degree for each fuzzy goal as the importance of the fuzzy goal. In this model, the more important the goals, the higher the desirable achievement degrees.

If desirable achievement degrees 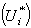for fuzzy multi-target goals are defined by the decision maker then the same method of Chen and Tsai can be introduced into the general formulation of (GP-MFTI) by adding the constraints 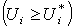which means the importance of goals.

4. An Illustrative Example

Let us consider a (GP-MFTI) problem with three goals and three constraints. The information about these goals and constraints are shown in table 1:

Table 1. Information about the three fuzzy goals

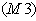Basing on the linear multi-target functions (MTFs), the above problem can be formulated using the form of as follows: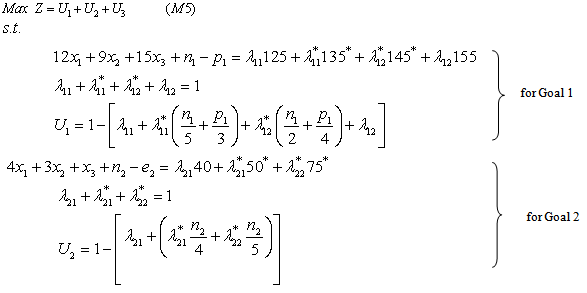

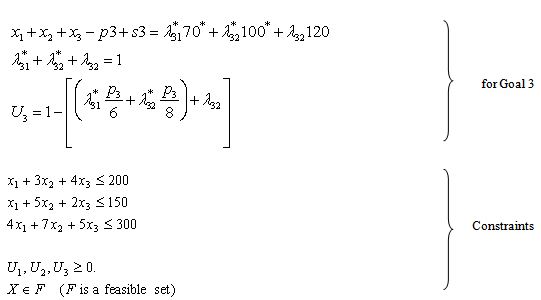where 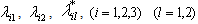are binary variables, and are considered as general variables, because they represent the quantity of products. This problem is solved using LINGO[21] to obtain the optimal solution as: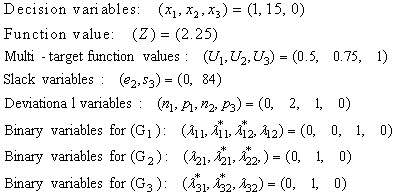

It can be seen from the optimal solution that goals 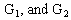are not completely satisfied, whereas goal 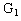is completely satisfied. According to the decision maker’s preferences, the value of 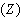could be translated in term of a realization percentage of the goals specified by the manager. This value ranges from 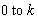(where 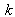represents the number of the goals). Therefore, the closer 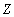in this example is to the value 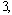the more globally satisfied the manager should be with the solution obtained.

5. Discussion and Conclusions

In this paper, the formulations of MCGP proposed by Chang, and Ustun are stated, and we have given some suggestions for their improvement. A new model for solving general goal programming with multi fuzzy-target (GP-MFTI) problems is proposed by introducing all the types of the functions which exist in the real world situations where the concept of multi-target functions is used that allow the decision maker to express explicitly his preferences. The properties of this new model are stated and proved with the reviewed models. The absolute values of deviation variables are used in this model and appeared in the optimal solutions because the decision maker is interested in using them for further analysis. The (GP-MFTI) formulation uses the concept of the indifference and veto thresholds to characterize the imprecision and the preferences related to all types of the existing goals. The (GP-MFTI) can be applied in different domains of management and economics in real decision making problems in the future researches like: Manpower planning, Project selection, Hospital administration, Academic resource allocation, Transportation problems, Portfolio selection, Determination of time standards, Multi-plant/product aggregate production loading, Quality control system, and other disciplines.

(GP-MFTI) is considered as an extension of MCGP. Therefore, the classical models of decision making including goal programming (GP), fuzzy goal programming (FGP), and MCGP are considered as special cases of the proposed model (GP-MFTI). Finally, we can qualify this model as a tool of multi-criterion decision aid.