Nejmaddin A. Suleiman, Maher A. Nawkhass
Department of Mathematics, College of Education, University of Salahaddin-Erbil-Iraq
Correspondence to: Maher A. Nawkhass, Department of Mathematics, College of Education, University of Salahaddin-Erbil-Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper uses Optimal Average maximin and minimax value techniques to transform multi-objective quadratic fractional programming problems (MOQFPP) to single QFPP. An algorithm is proposed for solvingsuch problems. We also solved the problem by Chandra Sen. technique, mean & median techniques. The resultsfrom the latter techniquesare obtained and compared to the result of maximin and minimax technique. This work has been tested through several numerical examples; only two of them are presented in this work. The numerical results in this paper indicate that our technique is promising.
Keywords:
MOQFPP, Chandra Sen, Mean, Median, Optimal Average of Maximin & Minimax Techniques
Cite this paper: Nejmaddin A. Suleiman, Maher A. Nawkhass, Transforming and Solving Multi-objective Quadratic Fractional Programming Problems by Optimal Average of Maximin & Minimax Techniques, American Journal of Operational Research, Vol. 3 No. 3, 2013, pp. 92-98. doi: 10.5923/j.ajor.20130303.03.
1. Introduction
A quadratic fractional form is a mathematical expression of the type 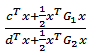 where
where 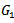 and
and 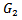 are
are 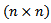 matrix of coefficients and they are symmetric matrixes. All vectors are assumed to be column vectors unless transposed
matrix of coefficients and they are symmetric matrixes. All vectors are assumed to be column vectors unless transposed 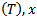 is an n-dimensional vector of decision variables, c,d-are the n-dimensional vector of constants[10]. The term Programming refers to the processof determining a particular program or plan of action. So Quadratic Fractional Programming (QFP) is one of themost important optimization (maximization / minimization) techniques developed in the field of Operations Research (OR).A new modified simplex method[9] is used to solve special case of a quadratic fractional programming, a solution can be obtained by a set of simultaneous equations. However a unique solution for a set of simultaneous equations in n-variables
is an n-dimensional vector of decision variables, c,d-are the n-dimensional vector of constants[10]. The term Programming refers to the processof determining a particular program or plan of action. So Quadratic Fractional Programming (QFP) is one of themost important optimization (maximization / minimization) techniques developed in the field of Operations Research (OR).A new modified simplex method[9] is used to solve special case of a quadratic fractional programming, a solution can be obtained by a set of simultaneous equations. However a unique solution for a set of simultaneous equations in n-variables 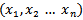 , at least one of them is non-zero, can be obtained if there are exactly n relations. When the number of relations is greater than or less than n, a unique solution cannot be exist but a number of trial solutions can be found.In various practical situations, the problems are seen in which the number of relations is notequal to the number of variables and many of the relations are in the form ofinequalities
, at least one of them is non-zero, can be obtained if there are exactly n relations. When the number of relations is greater than or less than n, a unique solution cannot be exist but a number of trial solutions can be found.In various practical situations, the problems are seen in which the number of relations is notequal to the number of variables and many of the relations are in the form ofinequalities 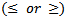 to maximize or minimize a quadratic fractional function of the variables subject to suchconditions. Such problems are known as Quadratic Fractional Programming Problem (QFPP). Quadratic Fractional programming problemhave attracted considerable research and interest, since they are useful in production planning, financial and corporative planning, health care and hospital planningThis work develops a new model of (MOQFPP) and suggested an algorithm to solve it, byusinga special case of objective function for (QFPP)as a form
to maximize or minimize a quadratic fractional function of the variables subject to suchconditions. Such problems are known as Quadratic Fractional Programming Problem (QFPP). Quadratic Fractional programming problemhave attracted considerable research and interest, since they are useful in production planning, financial and corporative planning, health care and hospital planningThis work develops a new model of (MOQFPP) and suggested an algorithm to solve it, byusinga special case of objective function for (QFPP)as a form 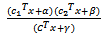 where
where 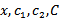 are (n × 1) column vectors, and α, β, γ are scalars and prime (T) denoted the transpose of the vector. A new technique optimal average of maximin & minimax is suggestedto solve MOQFPP withseveral method (Chandra Sen, mean, median) to compare between the results.In (1983), Chandra Sen[6] defined the multi-objective linear programming problem, and suggested an approach to construct multi-objective function under the limitation that the optimum values of individual problems are greater than zero.This technique use to solve MOLPP[7] and MOFPP[5] and apply the same technique to solve MOQFPP.Mean, median methods is used to transforms multi - objective to one combined objective function and solve it by previous ways, In (1997) a reference direction approach to multiple objective quadratic-linear programming, that studied by GuangYuan Yu and Pekka Korhonen[2], proposes an interactive procedure for solving multiple criteria problems with one quadratic objective, several linear objectives, and a set of linear constraints. The procedure is based on the use of reference directions and weighted sums.[4] Sulaiman and Sadiq (2006) studied the multi - objective function by solving the multi - objective programming problem, using mean and median value.(2006), Salwa and Emad Abass[8] studied and Construct mathematical models for solving multi-objective linear programming (MOLP) problem. Huey-Kuo Chen and Huey - Wen Chou[3] (1996) proposed a fuzzy approach, which induces some methodologies as special cases, for solving the multiple objective linear programming problem. Sulaiman & Abulrahim (2013) studied the transformation technique to solve multi-objective linear fractional programming problem [5]. (2008) Sulaiman and Hamadameen studied optimal transformation technique to solve multi-objective linear programming problem (MOLPP)[7].In this article, we aim to solve a multi objective quadratic fractional programming problem by optimal average of maximin & minimax (OAxn) which is reported in section (5.3) to minimizes cost and maximizes profit, Irrespective of the number objectives with less computational burden, Computer applications for the algorithm will been discussed by solving numerical examples.
are (n × 1) column vectors, and α, β, γ are scalars and prime (T) denoted the transpose of the vector. A new technique optimal average of maximin & minimax is suggestedto solve MOQFPP withseveral method (Chandra Sen, mean, median) to compare between the results.In (1983), Chandra Sen[6] defined the multi-objective linear programming problem, and suggested an approach to construct multi-objective function under the limitation that the optimum values of individual problems are greater than zero.This technique use to solve MOLPP[7] and MOFPP[5] and apply the same technique to solve MOQFPP.Mean, median methods is used to transforms multi - objective to one combined objective function and solve it by previous ways, In (1997) a reference direction approach to multiple objective quadratic-linear programming, that studied by GuangYuan Yu and Pekka Korhonen[2], proposes an interactive procedure for solving multiple criteria problems with one quadratic objective, several linear objectives, and a set of linear constraints. The procedure is based on the use of reference directions and weighted sums.[4] Sulaiman and Sadiq (2006) studied the multi - objective function by solving the multi - objective programming problem, using mean and median value.(2006), Salwa and Emad Abass[8] studied and Construct mathematical models for solving multi-objective linear programming (MOLP) problem. Huey-Kuo Chen and Huey - Wen Chou[3] (1996) proposed a fuzzy approach, which induces some methodologies as special cases, for solving the multiple objective linear programming problem. Sulaiman & Abulrahim (2013) studied the transformation technique to solve multi-objective linear fractional programming problem [5]. (2008) Sulaiman and Hamadameen studied optimal transformation technique to solve multi-objective linear programming problem (MOLPP)[7].In this article, we aim to solve a multi objective quadratic fractional programming problem by optimal average of maximin & minimax (OAxn) which is reported in section (5.3) to minimizes cost and maximizes profit, Irrespective of the number objectives with less computational burden, Computer applications for the algorithm will been discussed by solving numerical examples.
2. Quadratic Programming
If the optimization problem assumes the form 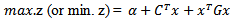 subject to:
subject to: 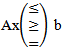
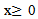 Where
Where 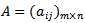 , matrix of coefficients,
, matrix of coefficients, 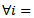
 and
and 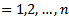 ,
, 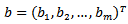 ,
, 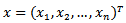 ,
, 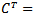
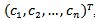 , and
, and 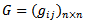 is a positive definite or positive semi-definite symmetric square matrix, moreover the constraints are linear and the objective function is quadratic. Such optimization problem is said to be a quadratic programming (QP) problem.[1]
is a positive definite or positive semi-definite symmetric square matrix, moreover the constraints are linear and the objective function is quadratic. Such optimization problem is said to be a quadratic programming (QP) problem.[1]
3. Mathematical Form of QFPP
The mathematical form of this type of problems is given as follows: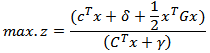
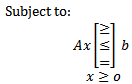 Where
Where 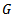 is
is 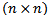 matrix of coefficients with
matrix of coefficients with 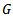 is symmetric matrixes. All vectors are assumed to be column vectors unless transposed (T). Where x is an n-dimensional vector of decision variables,
is symmetric matrixes. All vectors are assumed to be column vectors unless transposed (T). Where x is an n-dimensional vector of decision variables, 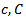 is the n-dimensional vector of constants, b is n -dimensional vector of constants.
is the n-dimensional vector of constants, b is n -dimensional vector of constants. 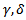 are scalars. In this work the problem that has objective function is tried to be solved has thefollowing form:
are scalars. In this work the problem that has objective function is tried to be solved has thefollowing form: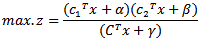
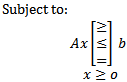 A is m × n matrix , all vectors are assumed to be column vectors unless transposed (T). where x is an n -dimensional vector of decision variables,
A is m × n matrix , all vectors are assumed to be column vectors unless transposed (T). where x is an n -dimensional vector of decision variables, 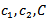 are the n -dimensional vector of constants, b is n -dimensional vector of constants,
are the n -dimensional vector of constants, b is n -dimensional vector of constants, 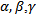 are scalars.[9]
are scalars.[9]
3.1. Solving QFPP by the Following Method
A new Modified Simplex Method is used to solve the numerical exampleto apply simplex process, first we find 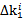 ,
, 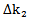 from the coefficient of numerator and denominator of objective function respectively, by using the following formula:
from the coefficient of numerator and denominator of objective function respectively, by using the following formula: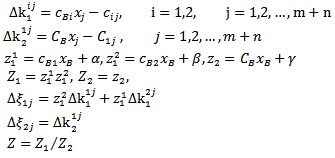 In this approach we define the formula to find
In this approach we define the formula to find 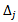 from
from 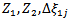 and
and 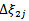 as follows:
as follows: 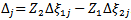 . For more detail see[9] p. 3756.
. For more detail see[9] p. 3756.
3.2. Algorithm for Solving QFPP by New Modified Simplex Method
An algorithm to solve QFPP by Modified Simplex Method is presented in reference[9] p.3756 and p. 3757.
4. Multi-Objective Quadratic Fractional Programming Problem
Multi-Objective functions are the ratio of two objective functions thathave quadratic objective function in numerator and linear objective function in denominator, this is said to be MOQFPP then can be defined: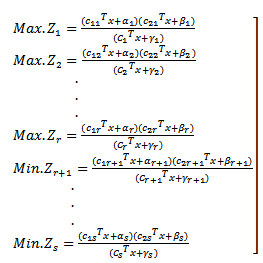 | (4.1) |
Subject to: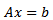 | (4.2) |
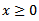 | (4.3) |
Where b is m-dimensional vector of constants, x is n-dimensional vector of decision variables, A is a m×n matrix of constants, r is number of objective functions to be maximized, s is the number of objective functions to be maximized and minimized and 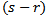 is the number of objective functions that is minimized. A is m × n matrix, all vectors are assumed to be column vectors unless transposed
is the number of objective functions that is minimized. A is m × n matrix, all vectors are assumed to be column vectors unless transposed 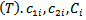 where i=1,…,s are the n-dimensional vector of constants
where i=1,…,s are the n-dimensional vector of constants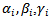 , where i =1,…,s are scalars.
, where i =1,…,s are scalars.
5. Solving MOQFPP by Using the Following Technique
5.1. Chandra Sen. Technique
The same approach which was taken by Sen. (1983)[6] is followed here to formulate the constraint objective function for the MOQFPP. Suppose we obtain a single value corresponding to each of the objective functions of the MOQFPP of equation (4.1).They are being optimized individually subject to the constraints (4.2) and (4.3) as follows: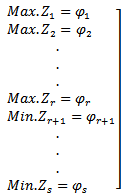 | (5.1.1) |
Where 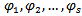 are values of the objective functions, which each objective function in 4.1 solved by section 3.3, the level of the decision variable may not necessarily be the same for all optimal solutions in presence of conflicts among objectives. But we require the common set of decision variables to be the best compromising optimal solution that we can determine for the common set of the decision variables from the following combined objective function, which formulate the MOQFPP given in following equation.
are values of the objective functions, which each objective function in 4.1 solved by section 3.3, the level of the decision variable may not necessarily be the same for all optimal solutions in presence of conflicts among objectives. But we require the common set of decision variables to be the best compromising optimal solution that we can determine for the common set of the decision variables from the following combined objective function, which formulate the MOQFPP given in following equation.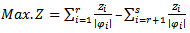 | (5.1.2) |
Where 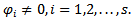 Subject to constraints (4.2) and (4.3), the optimum value of the objective functions
Subject to constraints (4.2) and (4.3), the optimum value of the objective functions 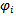
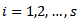 may be positive or negative. And
may be positive or negative. And 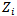 when i=1,…,r represents the max.z objective functions and when i= r+1 ,…,s min.z objective function in (4.1). Finally solve equation (5.1.2) with same constraint (4.2) and (4.3) by section 3.2.
when i=1,…,r represents the max.z objective functions and when i= r+1 ,…,s min.z objective function in (4.1). Finally solve equation (5.1.2) with same constraint (4.2) and (4.3) by section 3.2.
5.2. Mean and Median Modified Approach
We formulate the combined objective function as follows to determine the common set of decision variables,to solving the MOQFPP by modified approach (using mean and median value),[7],[5].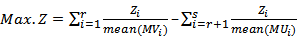 | (5.2.1) |
Subject to the same constraints (4.2), (4.3); Where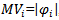 , for all
, for all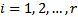 ;
; 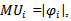 for all
for all 
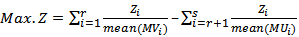 | (5.2.2) |
Subject to the same constraints (4.2), (4.3); Where 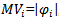 , for all
, for all 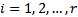 ;
;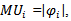 for all
for all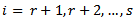
5.3. Optimal Average of Maximin & Minimax (OAxn) Techniques
We will define some definitions related with the Optimal Average (OAxn) techniques and introduce an algorithm for it.Definition1: let 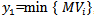 , where
, where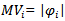 , and
, and 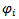 is the maximum value of
is the maximum value of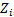 , for all
, for all 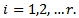 Definition 2: let
Definition 2: let 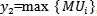 , where
, where 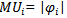 , and
, and 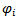 is the minimum value of
is the minimum value of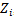 , for all
, for all 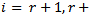
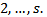 Definition 3: We denote the optimal average of maximin &minimax (OAxn), as follows:
Definition 3: We denote the optimal average of maximin &minimax (OAxn), as follows: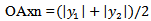 , where
, where 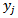 defined by definition(j), for all j=1,2 respectively
defined by definition(j), for all j=1,2 respectively
5.3.1. The Algorithm
The following algorithm is to obtain the optimal average of maximin & minimax for the multiobjective quadratic fractional programming problem and can be summarized as follows:- Step1: Write the standard form of the problem, by introducing slack and artificial variables to constraints, and write starting Simplex table. Step2: Calculate the 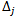 by the following formula
by the following formula 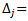
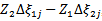 , then write it in the starting Simplex table.Step3: Find the solution of first objective problem by using Simplex process.Step4: Check the solution for feasibility in step3, if it is feasible then go to step5, otherwise use dual Simplex method to remove infeasibility.Step5: Check the solution for optimality if all
, then write it in the starting Simplex table.Step3: Find the solution of first objective problem by using Simplex process.Step4: Check the solution for feasibility in step3, if it is feasible then go to step5, otherwise use dual Simplex method to remove infeasibility.Step5: Check the solution for optimality if all 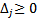 , then go to step6, otherwise back to step3. Step6: Assign a name to the optimum value of the maximum objective function
, then go to step6, otherwise back to step3. Step6: Assign a name to the optimum value of the maximum objective function 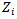 say
say 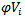 where i= i=1,2,…,r. and assign a name to the optimum value of the minimum objective function
where i= i=1,2,…,r. and assign a name to the optimum value of the minimum objective function 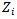 say
say 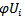 where i=
where i=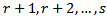 .Step7: Repeat process from the step 3; for i =2,…, s to be include all the objective problem.Step8: Select
.Step7: Repeat process from the step 3; for i =2,…, s to be include all the objective problem.Step8: Select 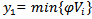 ,
, 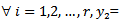
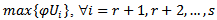 then calculate,
then calculate, 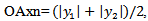 Step9: Optimize the combined objective function order the same constrains(4.2),(4.3) as:
Step9: Optimize the combined objective function order the same constrains(4.2),(4.3) as: 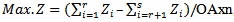 (5.3.1.1)
(5.3.1.1)
5.3.2. Program Notation
The following notations, which are used in computer program, aredefined as follows: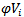 = The value of objective function which is to be maximized.
= The value of objective function which is to be maximized.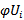 = The value of objective function which is to be minimized.
= The value of objective function which is to be minimized.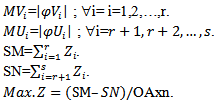
6. Numerical Examples
We solved several numerical examples, but only two of them are presented in this work.Example 1: 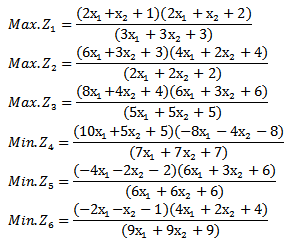
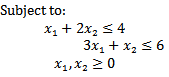 Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results are as below in table 1:
Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results are as below in table 1:Table 1. Results of example (1)
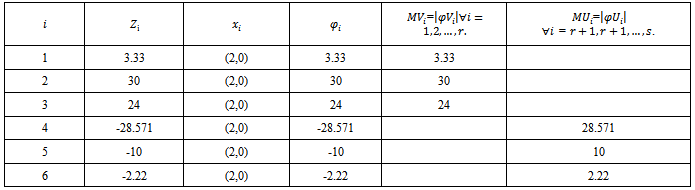 |
| |
|
(5.3.1.1) in section (5.3.1) is utilized insolving example (1) to find MOQFPP by usingoptimalaverage of maximin &minimax techniques: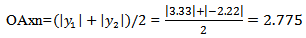 And
And 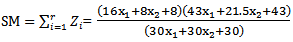 and
and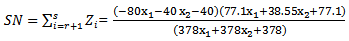 Then
Then 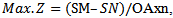
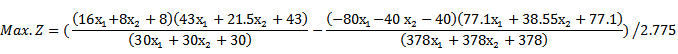 Then write the objective functions as following.
Then write the objective functions as following.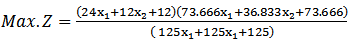 | (A1) |
Subject to given constraint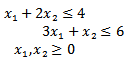 Now (A1) issolved by algorithm (3.2), then the optimal solution is found as follow
Now (A1) issolved by algorithm (3.2), then the optimal solution is found as follow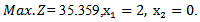 When (5.1.2) in section (5.1) is used tosolve example (1), to find MOQFPP by Chandra Sen. technique:We have
When (5.1.2) in section (5.1) is used tosolve example (1), to find MOQFPP by Chandra Sen. technique:We have 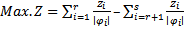 , the combined objective quadratic fractional function is
, the combined objective quadratic fractional function is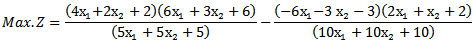 Then
Then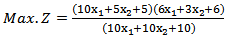 | (B1) |
Therefore. After solving (B1)by given a subjectwiththe same constraints as before, we find 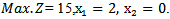 When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (1) to find MOQFPP by using mean and median respectively:First when we solve the example by using mean modified approach (5.2.1)Then the combined objective quadratic fractional function is
When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (1) to find MOQFPP by using mean and median respectively:First when we solve the example by using mean modified approach (5.2.1)Then the combined objective quadratic fractional function is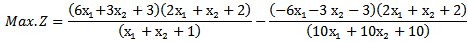 Then
Then 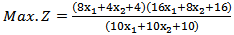 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 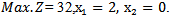 Second when we solve the example by using medianmodified approach (5.2.2) Then the combined objective quadratic fractional function is
Second when we solve the example by using medianmodified approach (5.2.2) Then the combined objective quadratic fractional function is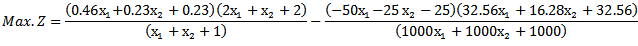 Then
Then 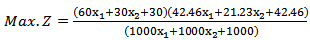 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 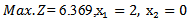 when using median modified approach
when using median modified approach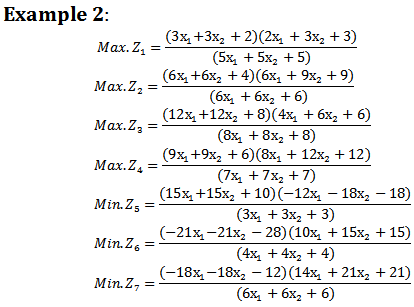
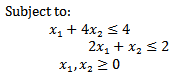 Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results as below in table 2:
Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results as below in table 2:Table 2. Results of example (2)
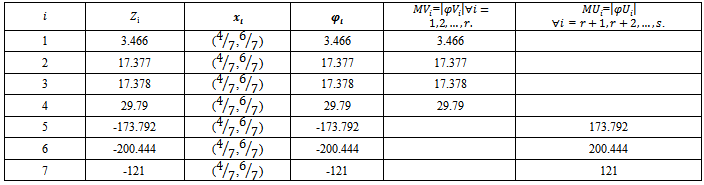 |
| |
|
(5.3.1.1) in section (5.3.1) is used tosolve the example (2) to find MOQFPP by usingoptimalaverage of maximin &minimax techniques: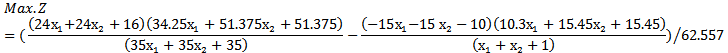 Then write the objective functions as following.
Then write the objective functions as following.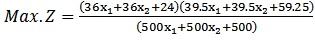 | (B1) |
Subject to 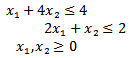 Now solving (B1) by algorithm (3.2) we get the optimal solution as follows.
Now solving (B1) by algorithm (3.2) we get the optimal solution as follows.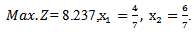 When (5.1.2) in section (5.1)is used to solve example (2),to find MOQFPP by usingChandra Sen. Technique:
When (5.1.2) in section (5.1)is used to solve example (2),to find MOQFPP by usingChandra Sen. Technique: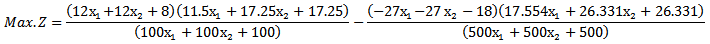 Then we have
Then we have 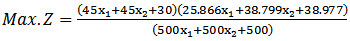 . Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
. Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 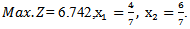 When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (2) to find MOQFPP by using mean and median respectively :First when we solve the example by using mean modified approach (5.2.1) Then the combined objective quadratic fractional function is
When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (2) to find MOQFPP by using mean and median respectively :First when we solve the example by using mean modified approach (5.2.1) Then the combined objective quadratic fractional function is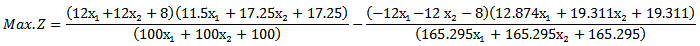 Then
Then 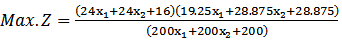 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 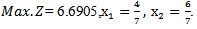 Second when we solve the example by using median modified approach (5.2.2) Then the combined objective quadratic fractional function is
Second when we solve the example by using median modified approach (5.2.2) Then the combined objective quadratic fractional function is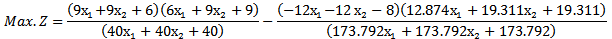 Then
Then 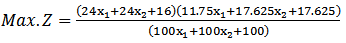 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 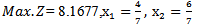
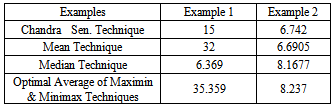
7. Comparison of the Numerical Results
Now, we are going to comparethe numerical results which are obtained of the examples above. The comparison is presented in in table 3 belowThe table 3 shows the results whichsolved by optimal Average approach was better than theResults which solved by other approaches.Table 3. Comparison between results of the numerical techniques
 |
| |
|
8. Conclusions
In This work, we have defined and discussed a number of techniques,the comparisons of these methods are based on the value of the objective function. After solving the numerical examples, we found that max.z which obtained by our technique is better than other techniques (Chandra Sen.,Mean&Median).
References
| [1] | A. Antoniou, Wu-Sheng Lu, Practical Optimization Algorithms and Engineering Applications, Department of Electrical and Computer Engineering University of Victoria, Canada. (2007). 675. |
| [2] | GuangYuan Yu, Pekka Korhonen, A reference direction approach to multiple objective quadratic-linear programming, European Journal of Operational Research 102 (1997) 601-610. |
| [3] | Huey-Kuo Chen, Huey-Wen Chou, Solving multiobjective linear programming problems - a generic approach, Fuzzy Sets and Systems, Volume 82, Issue 1, 26 August 1996, Pages 35–38. |
| [4] | Sulaiman, N.A. and Sadiq, Gulnar, W.,(2006),Solving the multi objective programming problemusing mean and median value, Ref.J. of comp & Math’s, Vol.3. |
| [5] | Sulaiman, N. A. & Abulrahim, Basiya K. March 2013,Using Transformation Technique To Solve Multi-Objective Linear Fractional Programming Problem,IJRRAS14 (3) . |
| [6] | Sen., Ch., (1983),A new approach for multi-objective rural development planning, The India Economic Journal, Vol. 30,No. 4,PP.91-96. |
| [7] | Sulaiman, N.A. and Hamadameen, Abdul-Qader O.(2008), Optimal Transformation Technique To Solve Multi - Objective Linear Programming Problem (MOLPP), Journal of Kirkuk University – Scientific Studies , vol.3, No.2. |
| [8] | Shakir, Salwa; Kuffi, Emad Abass, Construct mathematical models for solving multi-objective linear programming (MOLP) problem. (English summary), First Conference on Mathematical Sciences, 458–462, Zarqu Priv. Univ., Zarka, 2006. |
| [9] | Suleiman, N. A. and Nawkhass, M. A.(2013),A New Modified Simplex Method to Solve Quadratic Fractional Programming Problem and Compared it to a Traditional Simplex Method by Using Pseudoaffinity of Quadratic Fractional Functions, Applied Mathematical Sciences, Vol. 7, no. 76, 3749 – 3764. |
| [10] | Nejmaddin A. Suleiman, Maher A. Nawkhass, Solving Quadratic Fractional Programming Problem, International Journal of Applied Mathematical Research, 2 (2) (2013) 306. |
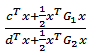 where
where 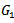 and
and 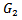 are
are 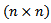 matrix of coefficients and they are symmetric matrixes. All vectors are assumed to be column vectors unless transposed
matrix of coefficients and they are symmetric matrixes. All vectors are assumed to be column vectors unless transposed 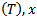 is an n-dimensional vector of decision variables, c,d-are the n-dimensional vector of constants[10]. The term Programming refers to the processof determining a particular program or plan of action. So Quadratic Fractional Programming (QFP) is one of themost important optimization (maximization / minimization) techniques developed in the field of Operations Research (OR).A new modified simplex method[9] is used to solve special case of a quadratic fractional programming, a solution can be obtained by a set of simultaneous equations. However a unique solution for a set of simultaneous equations in n-variables
is an n-dimensional vector of decision variables, c,d-are the n-dimensional vector of constants[10]. The term Programming refers to the processof determining a particular program or plan of action. So Quadratic Fractional Programming (QFP) is one of themost important optimization (maximization / minimization) techniques developed in the field of Operations Research (OR).A new modified simplex method[9] is used to solve special case of a quadratic fractional programming, a solution can be obtained by a set of simultaneous equations. However a unique solution for a set of simultaneous equations in n-variables 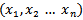 , at least one of them is non-zero, can be obtained if there are exactly n relations. When the number of relations is greater than or less than n, a unique solution cannot be exist but a number of trial solutions can be found.In various practical situations, the problems are seen in which the number of relations is notequal to the number of variables and many of the relations are in the form ofinequalities
, at least one of them is non-zero, can be obtained if there are exactly n relations. When the number of relations is greater than or less than n, a unique solution cannot be exist but a number of trial solutions can be found.In various practical situations, the problems are seen in which the number of relations is notequal to the number of variables and many of the relations are in the form ofinequalities 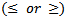 to maximize or minimize a quadratic fractional function of the variables subject to suchconditions. Such problems are known as Quadratic Fractional Programming Problem (QFPP). Quadratic Fractional programming problemhave attracted considerable research and interest, since they are useful in production planning, financial and corporative planning, health care and hospital planningThis work develops a new model of (MOQFPP) and suggested an algorithm to solve it, byusinga special case of objective function for (QFPP)as a form
to maximize or minimize a quadratic fractional function of the variables subject to suchconditions. Such problems are known as Quadratic Fractional Programming Problem (QFPP). Quadratic Fractional programming problemhave attracted considerable research and interest, since they are useful in production planning, financial and corporative planning, health care and hospital planningThis work develops a new model of (MOQFPP) and suggested an algorithm to solve it, byusinga special case of objective function for (QFPP)as a form 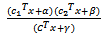 where
where 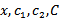 are (n × 1) column vectors, and α, β, γ are scalars and prime (T) denoted the transpose of the vector. A new technique optimal average of maximin & minimax is suggestedto solve MOQFPP withseveral method (Chandra Sen, mean, median) to compare between the results.In (1983), Chandra Sen[6] defined the multi-objective linear programming problem, and suggested an approach to construct multi-objective function under the limitation that the optimum values of individual problems are greater than zero.This technique use to solve MOLPP[7] and MOFPP[5] and apply the same technique to solve MOQFPP.Mean, median methods is used to transforms multi - objective to one combined objective function and solve it by previous ways, In (1997) a reference direction approach to multiple objective quadratic-linear programming, that studied by GuangYuan Yu and Pekka Korhonen[2], proposes an interactive procedure for solving multiple criteria problems with one quadratic objective, several linear objectives, and a set of linear constraints. The procedure is based on the use of reference directions and weighted sums.[4] Sulaiman and Sadiq (2006) studied the multi - objective function by solving the multi - objective programming problem, using mean and median value.(2006), Salwa and Emad Abass[8] studied and Construct mathematical models for solving multi-objective linear programming (MOLP) problem. Huey-Kuo Chen and Huey - Wen Chou[3] (1996) proposed a fuzzy approach, which induces some methodologies as special cases, for solving the multiple objective linear programming problem. Sulaiman & Abulrahim (2013) studied the transformation technique to solve multi-objective linear fractional programming problem [5]. (2008) Sulaiman and Hamadameen studied optimal transformation technique to solve multi-objective linear programming problem (MOLPP)[7].In this article, we aim to solve a multi objective quadratic fractional programming problem by optimal average of maximin & minimax (OAxn) which is reported in section (5.3) to minimizes cost and maximizes profit, Irrespective of the number objectives with less computational burden, Computer applications for the algorithm will been discussed by solving numerical examples.
are (n × 1) column vectors, and α, β, γ are scalars and prime (T) denoted the transpose of the vector. A new technique optimal average of maximin & minimax is suggestedto solve MOQFPP withseveral method (Chandra Sen, mean, median) to compare between the results.In (1983), Chandra Sen[6] defined the multi-objective linear programming problem, and suggested an approach to construct multi-objective function under the limitation that the optimum values of individual problems are greater than zero.This technique use to solve MOLPP[7] and MOFPP[5] and apply the same technique to solve MOQFPP.Mean, median methods is used to transforms multi - objective to one combined objective function and solve it by previous ways, In (1997) a reference direction approach to multiple objective quadratic-linear programming, that studied by GuangYuan Yu and Pekka Korhonen[2], proposes an interactive procedure for solving multiple criteria problems with one quadratic objective, several linear objectives, and a set of linear constraints. The procedure is based on the use of reference directions and weighted sums.[4] Sulaiman and Sadiq (2006) studied the multi - objective function by solving the multi - objective programming problem, using mean and median value.(2006), Salwa and Emad Abass[8] studied and Construct mathematical models for solving multi-objective linear programming (MOLP) problem. Huey-Kuo Chen and Huey - Wen Chou[3] (1996) proposed a fuzzy approach, which induces some methodologies as special cases, for solving the multiple objective linear programming problem. Sulaiman & Abulrahim (2013) studied the transformation technique to solve multi-objective linear fractional programming problem [5]. (2008) Sulaiman and Hamadameen studied optimal transformation technique to solve multi-objective linear programming problem (MOLPP)[7].In this article, we aim to solve a multi objective quadratic fractional programming problem by optimal average of maximin & minimax (OAxn) which is reported in section (5.3) to minimizes cost and maximizes profit, Irrespective of the number objectives with less computational burden, Computer applications for the algorithm will been discussed by solving numerical examples. 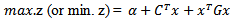 subject to:
subject to: 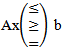
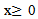 Where
Where 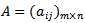 , matrix of coefficients,
, matrix of coefficients, 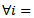
 and
and 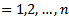 ,
, 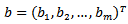 ,
, 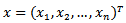 ,
, 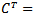
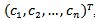 , and
, and 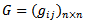 is a positive definite or positive semi-definite symmetric square matrix, moreover the constraints are linear and the objective function is quadratic. Such optimization problem is said to be a quadratic programming (QP) problem.[1]
is a positive definite or positive semi-definite symmetric square matrix, moreover the constraints are linear and the objective function is quadratic. Such optimization problem is said to be a quadratic programming (QP) problem.[1]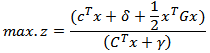
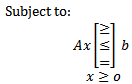 Where
Where 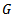 is
is 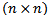 matrix of coefficients with
matrix of coefficients with 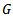 is symmetric matrixes. All vectors are assumed to be column vectors unless transposed (T). Where x is an n-dimensional vector of decision variables,
is symmetric matrixes. All vectors are assumed to be column vectors unless transposed (T). Where x is an n-dimensional vector of decision variables, 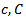 is the n-dimensional vector of constants, b is n -dimensional vector of constants.
is the n-dimensional vector of constants, b is n -dimensional vector of constants. 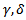 are scalars. In this work the problem that has objective function is tried to be solved has thefollowing form:
are scalars. In this work the problem that has objective function is tried to be solved has thefollowing form: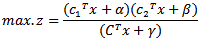
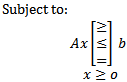 A is m × n matrix , all vectors are assumed to be column vectors unless transposed (T). where x is an n -dimensional vector of decision variables,
A is m × n matrix , all vectors are assumed to be column vectors unless transposed (T). where x is an n -dimensional vector of decision variables, 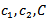 are the n -dimensional vector of constants, b is n -dimensional vector of constants,
are the n -dimensional vector of constants, b is n -dimensional vector of constants, 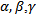 are scalars.[9]
are scalars.[9]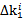 ,
, 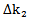 from the coefficient of numerator and denominator of objective function respectively, by using the following formula:
from the coefficient of numerator and denominator of objective function respectively, by using the following formula: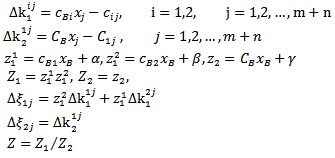 In this approach we define the formula to find
In this approach we define the formula to find 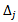 from
from 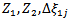 and
and 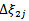 as follows:
as follows: 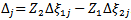 . For more detail see[9] p. 3756.
. For more detail see[9] p. 3756.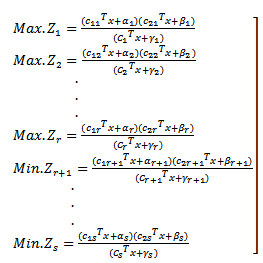
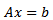
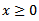
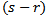 is the number of objective functions that is minimized. A is m × n matrix, all vectors are assumed to be column vectors unless transposed
is the number of objective functions that is minimized. A is m × n matrix, all vectors are assumed to be column vectors unless transposed 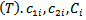 where i=1,…,s are the n-dimensional vector of constants
where i=1,…,s are the n-dimensional vector of constants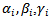 , where i =1,…,s are scalars.
, where i =1,…,s are scalars.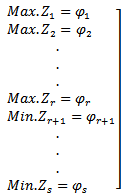
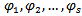 are values of the objective functions, which each objective function in 4.1 solved by section 3.3, the level of the decision variable may not necessarily be the same for all optimal solutions in presence of conflicts among objectives. But we require the common set of decision variables to be the best compromising optimal solution that we can determine for the common set of the decision variables from the following combined objective function, which formulate the MOQFPP given in following equation.
are values of the objective functions, which each objective function in 4.1 solved by section 3.3, the level of the decision variable may not necessarily be the same for all optimal solutions in presence of conflicts among objectives. But we require the common set of decision variables to be the best compromising optimal solution that we can determine for the common set of the decision variables from the following combined objective function, which formulate the MOQFPP given in following equation.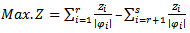
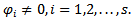 Subject to constraints (4.2) and (4.3), the optimum value of the objective functions
Subject to constraints (4.2) and (4.3), the optimum value of the objective functions 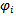
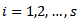 may be positive or negative. And
may be positive or negative. And 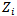 when i=1,…,r represents the max.z objective functions and when i= r+1 ,…,s min.z objective function in (4.1). Finally solve equation (5.1.2) with same constraint (4.2) and (4.3) by section 3.2.
when i=1,…,r represents the max.z objective functions and when i= r+1 ,…,s min.z objective function in (4.1). Finally solve equation (5.1.2) with same constraint (4.2) and (4.3) by section 3.2.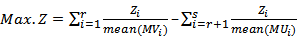
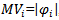 , for all
, for all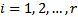 ;
; 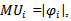 for all
for all 
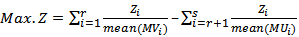
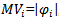 , for all
, for all 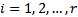 ;
;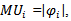 for all
for all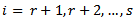
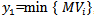 , where
, where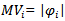 , and
, and 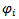 is the maximum value of
is the maximum value of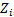 , for all
, for all 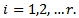 Definition 2: let
Definition 2: let 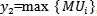 , where
, where 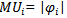 , and
, and 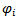 is the minimum value of
is the minimum value of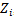 , for all
, for all 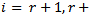
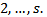 Definition 3: We denote the optimal average of maximin &minimax (OAxn), as follows:
Definition 3: We denote the optimal average of maximin &minimax (OAxn), as follows: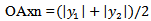 , where
, where 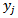 defined by definition(j), for all j=1,2 respectively
defined by definition(j), for all j=1,2 respectively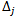 by the following formula
by the following formula 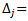
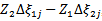 , then write it in the starting Simplex table.Step3: Find the solution of first objective problem by using Simplex process.Step4: Check the solution for feasibility in step3, if it is feasible then go to step5, otherwise use dual Simplex method to remove infeasibility.Step5: Check the solution for optimality if all
, then write it in the starting Simplex table.Step3: Find the solution of first objective problem by using Simplex process.Step4: Check the solution for feasibility in step3, if it is feasible then go to step5, otherwise use dual Simplex method to remove infeasibility.Step5: Check the solution for optimality if all 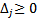 , then go to step6, otherwise back to step3. Step6: Assign a name to the optimum value of the maximum objective function
, then go to step6, otherwise back to step3. Step6: Assign a name to the optimum value of the maximum objective function 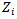 say
say 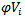 where i= i=1,2,…,r. and assign a name to the optimum value of the minimum objective function
where i= i=1,2,…,r. and assign a name to the optimum value of the minimum objective function 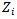 say
say 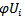 where i=
where i=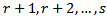 .Step7: Repeat process from the step 3; for i =2,…, s to be include all the objective problem.Step8: Select
.Step7: Repeat process from the step 3; for i =2,…, s to be include all the objective problem.Step8: Select 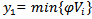 ,
, 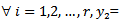
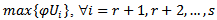 then calculate,
then calculate, 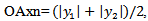 Step9: Optimize the combined objective function order the same constrains(4.2),(4.3) as:
Step9: Optimize the combined objective function order the same constrains(4.2),(4.3) as: 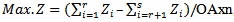 (5.3.1.1)
(5.3.1.1)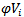 = The value of objective function which is to be maximized.
= The value of objective function which is to be maximized.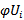 = The value of objective function which is to be minimized.
= The value of objective function which is to be minimized.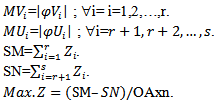
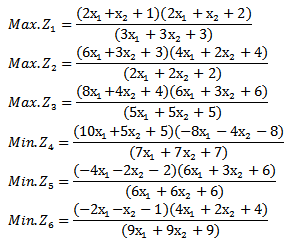
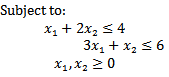 Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results are as below in table 1:
Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results are as below in table 1: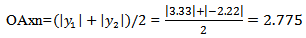 And
And 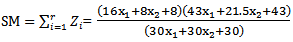 and
and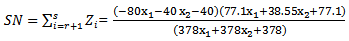 Then
Then 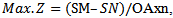
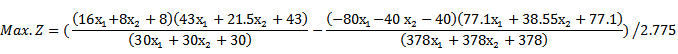 Then write the objective functions as following.
Then write the objective functions as following.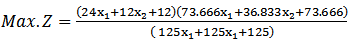
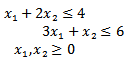 Now (A1) issolved by algorithm (3.2), then the optimal solution is found as follow
Now (A1) issolved by algorithm (3.2), then the optimal solution is found as follow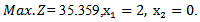 When (5.1.2) in section (5.1) is used tosolve example (1), to find MOQFPP by Chandra Sen. technique:We have
When (5.1.2) in section (5.1) is used tosolve example (1), to find MOQFPP by Chandra Sen. technique:We have 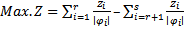 , the combined objective quadratic fractional function is
, the combined objective quadratic fractional function is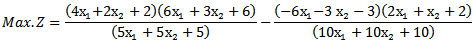 Then
Then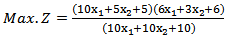
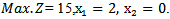 When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (1) to find MOQFPP by using mean and median respectively:First when we solve the example by using mean modified approach (5.2.1)Then the combined objective quadratic fractional function is
When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (1) to find MOQFPP by using mean and median respectively:First when we solve the example by using mean modified approach (5.2.1)Then the combined objective quadratic fractional function is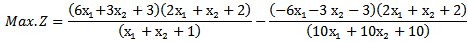 Then
Then 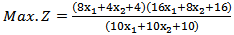 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 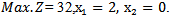 Second when we solve the example by using medianmodified approach (5.2.2) Then the combined objective quadratic fractional function is
Second when we solve the example by using medianmodified approach (5.2.2) Then the combined objective quadratic fractional function is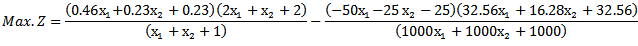 Then
Then 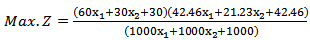 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 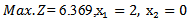 when using median modified approach
when using median modified approach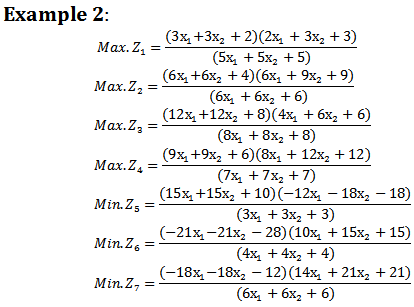
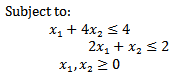 Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results as below in table 2:
Solution: After finding the value of each of individual objective functions by an algorithm of section (3.2) the results as below in table 2: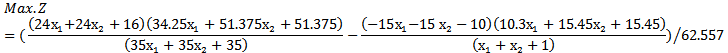 Then write the objective functions as following.
Then write the objective functions as following.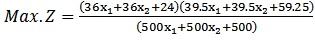
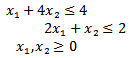 Now solving (B1) by algorithm (3.2) we get the optimal solution as follows.
Now solving (B1) by algorithm (3.2) we get the optimal solution as follows.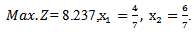 When (5.1.2) in section (5.1)is used to solve example (2),to find MOQFPP by usingChandra Sen. Technique:
When (5.1.2) in section (5.1)is used to solve example (2),to find MOQFPP by usingChandra Sen. Technique: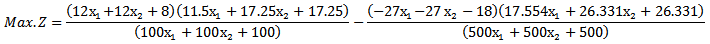 Then we have
Then we have 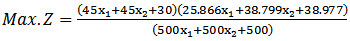 . Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
. Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 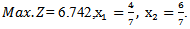 When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (2) to find MOQFPP by using mean and median respectively :First when we solve the example by using mean modified approach (5.2.1) Then the combined objective quadratic fractional function is
When (5.2.1) and (5.2.2) in section (5.2) are used to solve example (2) to find MOQFPP by using mean and median respectively :First when we solve the example by using mean modified approach (5.2.1) Then the combined objective quadratic fractional function is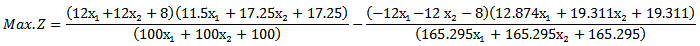 Then
Then 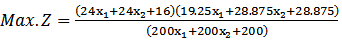 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 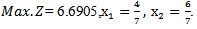 Second when we solve the example by using median modified approach (5.2.2) Then the combined objective quadratic fractional function is
Second when we solve the example by using median modified approach (5.2.2) Then the combined objective quadratic fractional function is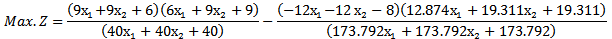 Then
Then 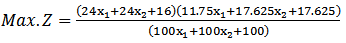 Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find
Therefore. After solving Max.Z by given a subjectwith the same constraints as before, we find 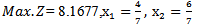
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

