P. Tirupathi Rao1, B. N. Naveen Kumar2, P. R. S. Reddy2
1Dept. of Statistics, Pondicherry University, Puducherry, 605014
2Dept. of Statistics, S.V. University, Tirupati, 517 502
Correspondence to: P. Tirupathi Rao, Dept. of Statistics, Pondicherry University, Puducherry, 605014.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, a stochastic programming problem is formulated for optimal drug administration to the cancer patients under chemotherapy. A stochastic model for three-stage cancer growth[1] has been considered for formulating the objective function and constraints. The objective of the problem is to maximize the drug efficacy subject to the constraints on the admissible protocols of healthy drug administration. The health status of the patient during drug presence and its absence can be evaluated through the developed model. Numerical illustrations were given for better understanding the model. This study will have extensive uses for health care industry in optimal chemotherapy.
Keywords:
Optimal Drug Administration, Stochastic Programming, Cancer Chemotherapy, Healthcare Management
Cite this paper: P. Tirupathi Rao, B. N. Naveen Kumar, P. R. S. Reddy, Stochastic Programming on Optimal Drug Administration for Three-Stage Cancer Chemotherapy Treatment, American Journal of Operational Research, Vol. 3 No. 2, 2013, pp. 65-74. doi: 10.5923/j.ajor.20130302.06.
1. Introduction
Cancer is a disease of division or proliferation of cells on abnormal, uninterrupted and continuous manner after formal initiation of cancer causing cell after mutant behaviour of a normal cell. The formation of malignancy is a resulting stage of transformation of normal cell division. This mechanism may be in stages, such as (i) Forming of mutant cell from normal cell (stage I); (ii) Formulation of pre malignant cell from mutant cell (stage II); and (iii) further transformation of pre-malignant cell in to malignant cell (stage-III). We will observe the faster growth rate among cell division when a normal cell is converted in to a malignant cell. It may be due to many unexplained reasons. In fact, there is no exact proposition on the cause of formation and growth of cancer cells. The genetical impacts, inactivation of alleles, formation location of cancer causing cell, the type of tissue and many more similar reasons may be the influencing factors of cancer growth. Identification of cancer at initial stages will be helpful to avoid the ultimate risk of death. The living body system has its own system of regulation and control over cell division and growth/loss processes of cells. The immunity system of the body will act as a defensive mechanism to protect the existing normal cells from invading mutant cells. This situation may leads to a considerable loss of white blood cells (WBC). Sometimes the active immune system may be responsible for the count of WBC beyond the upper threshold limit, which may cause the problems like leukemia (blood cancer). Hence the size of WBC either way at abnormal extremes is unwanted.Chemotherapy is a treatment of cancer control with a combination of drugs, usually administered in cycles with different intensified spells within the cycle. It has some considerable negative impacts also. It may harm some healthy and normal cells, though the objective of drug administration is to kill the cancer causing cells. In such cases, the WBC may come to the rescue of protecting normal and healthy cells. Consequently, there is a possibility of WBC loss. Continuous drug administration leads to health hazards due to the loss of normal cells and white blood cells. Hence, the patient needs periodic health checkups to assess the status levels of WBC. If the loss of WBC is considerably high then they have to be allowed to drug vacation to get recovery from the chemical toxicity of drugs. However, drug vacation may leads to re-aggravate the growth of mutant cell population. Therefore, both long-term drug administration and long-term drug vacation are unwanted. Regarding the drug dosage levels, drug administration above the required quantity will harm the natural immunity system by killing both normal and white blood cells. On the other hand, the drug quantity less than the required level will make the body drug resistant. Hence, there is a need of maintaining the optimal levels in drug doses for chemotherapy patient. The growth and loss behaviour of both normal and mutant cells are greatly influenced by the condition of drug administration and drug vacation. The applications of engineering optimal control theory to investigate the drug regimen for reducing an exponential tumor cell population have been studied[2,3]. The cancer chemotherapy optimization and computing models were developed by branching processes[4]. Toxicity limits are used to develop a model on optimal control for cancer chemotherapy[5,6]. The treatment of tumor over a fixed period of time by the repeated administration of a single drug is described by an optimal parameter selection model of cancer chemotherapy[7]. A protocol for drug administration to the tumor with immune resistance was mathematically modeled[8]. A single drug administration was applied for optimal cancer chemotherapy[9]. Optimized drug regimens by an efficacy-toxicity in cancer chemotherapy were modeled mathematically[10]. Stochastic model for optimal drug administration in cancer chemotherapy have been developed[11]. The problem of optimal administration of chemotherapeutic agents has been discussed for the treatment of brain tumors[12]. Treatment dependent malignancy growth was modeled with stochasticity and a stochastic programming approach is used for optimal drug administration in the treatment of two-stage cancer[13,14]. An approach of stochastic programming problem was developed for optimal drug administration for cancer chemotherapy[15].There was much emphasis on the usage of mathematical modeling on the studies of cancer growth by deterministic and stochastic assumptions. Very few available evidences are there in stochastic modeling of cancer growth during chemotherapy and also on optimization modeling of drug administration. In this study, a stochastic programming problem is developed for maximizing the drug effectiveness in 3-stage cancer chemotherapy. The phenomena of cell division, growth and loss of various stages are modeled with stochastic assumptions by Tirupathi Rao et.al[1]. Three-way Poisson process was used to develop the basic stochastic model. The mathematical formulae for the expected number of cells at stage-I, stage-II and stage-III; the variance of number of cells at stage-I, stage-II and stage-III were derived. These derived relations have been used for formulating the objective function and the constraints of the proposed programming problem. The constraint on healthy threshold limits of WBC is also considered. The decision parameters like rate of growth of mutant (stage-I) cells, premalignant (stage-II) cells, malignant (stage-III) cells; the rate of transformations from mutancy (stage-I) to pre-malignancy (stage-II), from pre-malignancy (stage-II) to malignancy (stage-III); and the death rates of mutant (stage-I) cells, premalignant (stage-II) cells, malignant (stage-III) cells in a tumor, etc are obtained with the study.
2. Stochastic Model and Statistical Components
It is assumed that a mutant (stage-I) cell may be either transformed to a premalignant (stage-II) cell or it may get death. A premalignant (stage-II) cell is either transformed to malignant (stage-III) cells or it may get death. The malignant (stage-III) cell either divided in to further malignant cells or it may get death. The behaviour of the cell division is influenced by the presence and absence of drug. The Statistical measures such as Average number of mutant (stage-I) cells; Average number of premalignant (stage-II) cells; and Average number of malignant (stage-III) cells during drug administration are denoted by E(NA), E(MA) and E(KA) respectively and Similarly the average number of cells in stage-I, stage-II and stage-III during drug vacation are denoted by E(NV), E(MV) and E(KV) respectively. The patient’s health status during presence and absence of drug are to be considered as complementary event. Therefore, the total effect of cell loss/growth is a linear combination of both drug presence and its absence. Let ‘X’ be the number of cells in a specific category. Then the expected number of cells during the drug administration and drug vacation is defined as aE(X)+(1-a)E(X); where a=1, when drug is administered; a=0, when drug is not administered.Let α1, β1, γ1 be the rates of generation of stage-I cells from normal cells; stage II cells from stage-I; stage-III cells from stage-II respectively during drug presence. Let λ1, δ1, θ1 be the rates of deaths cells from stage-I, stage-II, stage-III respectively during drug presence. Similarly the rates of generation of stage-I, stage-II and stage-III cells are α0, β0, γ0 during drug absence. λ0, δ0, θ0 are the rates of deaths of stage-I, stage-II and stage-III cells during drug absence. It is assumed that α, β, γ, λ, δ, θ are the linear combinations expressed as α = a.α0+(1-a).α1; β = b. β 0+(1-b).β 1; γ = c. γ 0+(1-c).γ 1; λ = d. λ 0+(1-d).λ 1; δ = e. δ 0+(1-e).δ 1; θ = f. θ 0+(1-f). θ 1 for a, b, c, d, e, f, g are equal to either ‘0’ or ‘1’. The schematic diagram show below shall explain the above mechanism of cell division and growth in detail.From the work of Tirupathi Rao et.al. (2012), the derived relations from the model are The expected number of mutant (stage-I) cells in a tumor at time t during drug administration is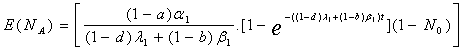 | (2.1) |
The expected number of premalignant (stage-II) cells in a tumor at time t during drug administration is 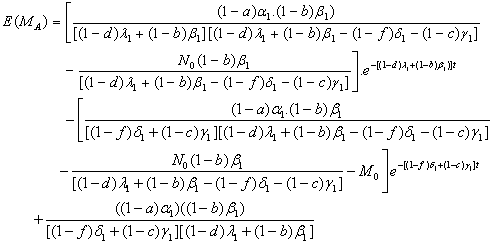 | (2.2) |
The expected number of malignant (stage-III) cells in a tumor at time t during drug administration is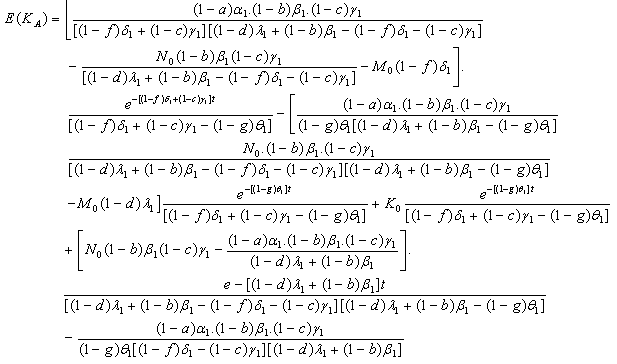 | (2.3) |
The expected number of mutant (stage-I) cells in a tumor at time t during drug vacation is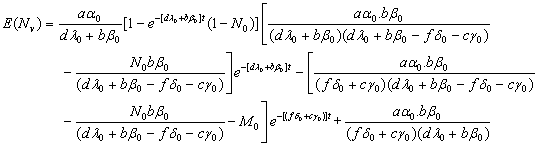 | (2.4) |
The expected number of premalignant (stage-II) cells in a tumor at time‘t’ during drug vacation is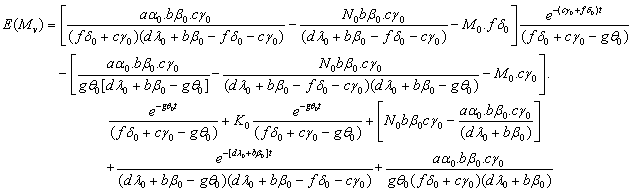 | (2.5) |
The expected number of malignant (stage-III) cells in a tumor at time‘t’ during drug vacation is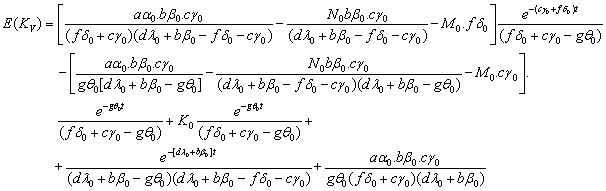 | (2.6) |
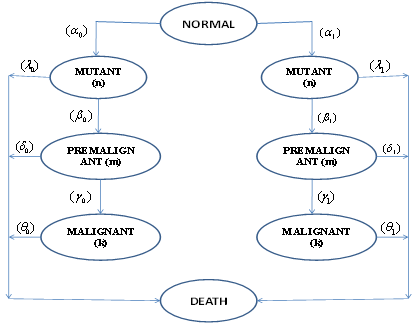 | Figure 1. The schematic diagram for the spread of 3 stage cancer |
3. Stochastic Programming Problem
in this section, the procedure for formulation of optimizations programming problem is discussed. The objective is on maximizing the drug's net effectiveness (pooling the positive, negative effectiveness) of drug on killing of cancer causing cells at all stages.
3.1. Notation and Terminology
i : Number of drug cycles in overall treatment of chemotherapy; i=1,2,… ;
;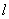 : Maximum number of drug cycles;j : Number of spells of drug administration in each cycle; j=1,2, …k; k : Maximum number of drug spells within a cycle; r : Number of drug vacation periods in the total treatment process; r=1,2, …
: Maximum number of drug cycles;j : Number of spells of drug administration in each cycle; j=1,2, …k; k : Maximum number of drug spells within a cycle; r : Number of drug vacation periods in the total treatment process; r=1,2, …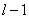 ; s : Number of days within a period of drug vacation; s=1,2, …
; s : Number of days within a period of drug vacation; s=1,2, …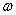 ;
;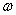 : Maximum number of days within a drug vacation period. aij: Number of units of drug doses in ith cycle and jth spell of drug administration (DA); pij : Positive (+ ve) effect of one unit DA on a mutant(stage-I) cell during ith cycle and jth spell; qij: Negative (- ve) effect of one unit DA on a mutant(stage-I)cell during ith cycle and jth spell; bij: +ve effect of one unit DA on a premalignant (stage-II) cell during ith cycle and jth spell; cij : -ve effect of one unit of DA on one premalignant (stage-II) cell during ith cycle and jth spell; uij : +ve effect of one unit DA on one malignant (stage-III) cell during ith cycle and jth spell; vij : - ve effect of one unit of DA on one malignant (stage-III) cell during ith cycle and jth spell; αij: Loss of WBC in one unit of DA for killing of one stage-I cell in ith cycle and jth spell; βij: Loss of WBC in one unit of DA for killing of one stage-II cell in ith cycle and jth spell; γij: Loss of WBC in one unit of DA for killing of one stage-III cell in ith cycle and jth spell;drs:+ve impact of one unit of drug vacation (DV) time on one "stage-I" cell in rth DV period, sth day; ers: - ve impact of one unit time of DV on one "stage-I" cell in rth DV period and sth day; frs: +ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; grs: - ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; mrs: +ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; nrs: - ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; λrs: Loss of WBC per unit time of DV due to growth of one "stage-I" cell in rth DV period, sth day; δrs: Loss of WBC per unit time of DV due to growth of one "stage-II" cell in rth DV perood, sth day; θrs: Loss of WBC per unit time of DV due to growth of one "stage-III" cell in rth DV period, sth day; trs : The number of time units in rth DV Period and sth day ; for r = 1,2, …; s = 1,2,….n Tx,y,z: Total +ve /-ve (x) effect of treatment during drug presence/absence(y) while targeting the Mutant/ Premalignant/ Malignant (z) cell population.Where x=1: If drug has positive effectiveness; x =0: If drug has negative effectivenessy=1: If Drug is present; y=0: If Drug is absentz=1: If the cell is in "stage-1" ; z=2: If the cell is in "stage-2"; z=3: If the cell is in "stage-3";WX,Y,Z: Total loss/growth(X) of WBC during drug presence/absence(Y) while targeting to destroy Mutant/ Premalignant/Malignant (Z) cell population.Where X=1: If there is Growth of WBC; X =0: If there is Loss of WBCY=1: During Drug Presence; Y=0: During Drug AbsenceZ=1: For Mutant cell; Z=2: For Premalignant cell; Z=3: For Malignant cellWU, WL: The desired optimal upper & lower limits of healthy sizes of WBC during treatment. NU, NL : The critical target upper & lower limits on size of the mutant (stage-I) cells MU, ML: The critical target limit upper & lower limits on size of the premalignant (stage-II) cells.KU, KL : The critical target upper and lower limits on size of the malignant (stage-III) cells
: Maximum number of days within a drug vacation period. aij: Number of units of drug doses in ith cycle and jth spell of drug administration (DA); pij : Positive (+ ve) effect of one unit DA on a mutant(stage-I) cell during ith cycle and jth spell; qij: Negative (- ve) effect of one unit DA on a mutant(stage-I)cell during ith cycle and jth spell; bij: +ve effect of one unit DA on a premalignant (stage-II) cell during ith cycle and jth spell; cij : -ve effect of one unit of DA on one premalignant (stage-II) cell during ith cycle and jth spell; uij : +ve effect of one unit DA on one malignant (stage-III) cell during ith cycle and jth spell; vij : - ve effect of one unit of DA on one malignant (stage-III) cell during ith cycle and jth spell; αij: Loss of WBC in one unit of DA for killing of one stage-I cell in ith cycle and jth spell; βij: Loss of WBC in one unit of DA for killing of one stage-II cell in ith cycle and jth spell; γij: Loss of WBC in one unit of DA for killing of one stage-III cell in ith cycle and jth spell;drs:+ve impact of one unit of drug vacation (DV) time on one "stage-I" cell in rth DV period, sth day; ers: - ve impact of one unit time of DV on one "stage-I" cell in rth DV period and sth day; frs: +ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; grs: - ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; mrs: +ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; nrs: - ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; λrs: Loss of WBC per unit time of DV due to growth of one "stage-I" cell in rth DV period, sth day; δrs: Loss of WBC per unit time of DV due to growth of one "stage-II" cell in rth DV perood, sth day; θrs: Loss of WBC per unit time of DV due to growth of one "stage-III" cell in rth DV period, sth day; trs : The number of time units in rth DV Period and sth day ; for r = 1,2, …; s = 1,2,….n Tx,y,z: Total +ve /-ve (x) effect of treatment during drug presence/absence(y) while targeting the Mutant/ Premalignant/ Malignant (z) cell population.Where x=1: If drug has positive effectiveness; x =0: If drug has negative effectivenessy=1: If Drug is present; y=0: If Drug is absentz=1: If the cell is in "stage-1" ; z=2: If the cell is in "stage-2"; z=3: If the cell is in "stage-3";WX,Y,Z: Total loss/growth(X) of WBC during drug presence/absence(Y) while targeting to destroy Mutant/ Premalignant/Malignant (Z) cell population.Where X=1: If there is Growth of WBC; X =0: If there is Loss of WBCY=1: During Drug Presence; Y=0: During Drug AbsenceZ=1: For Mutant cell; Z=2: For Premalignant cell; Z=3: For Malignant cellWU, WL: The desired optimal upper & lower limits of healthy sizes of WBC during treatment. NU, NL : The critical target upper & lower limits on size of the mutant (stage-I) cells MU, ML: The critical target limit upper & lower limits on size of the premalignant (stage-II) cells.KU, KL : The critical target upper and lower limits on size of the malignant (stage-III) cells
3.2. Programming Problem for Drug Administration
With the mentioned Terminology and notation,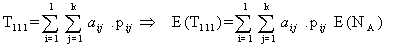 | (3.2.1) |
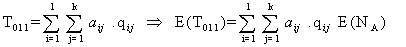 | (3.2.2) |
Implies the net effect of drug administration on one mutant (stage-I) cell is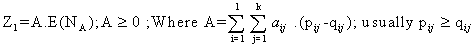 | (3.2.3) |
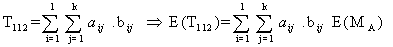 | (3.2.4) |
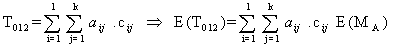 | (3.2.5) |
Implies the net effect of drug administration on a premalignant (stage-II) cell is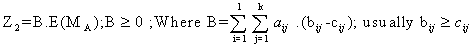 | (3.2.6) |
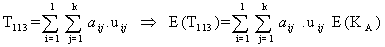 | (3.2.7) |
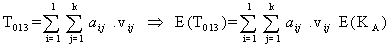 | (3.2.8) |
so as the net effect of drug administration on a malignant (stage-III) cell is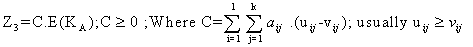 | (3.2.9) |
By considering 3.2.3, 3.2.6 and 3.2.9; the overall effect of drug administration on all the 3 types of cell population is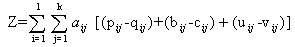 | (3.2.10) |
and Z is to be maximized.Regarding the constraints of the problem 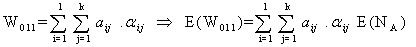 | (3.2.11) |
The constraint with respect to WBC loss count on mutant cells (stage-1) is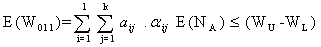 | (3.2.12) |
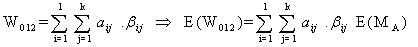 | (3.2.13) |
The constraint with respect to WBC loss count on premalignant (stage-2) cells is 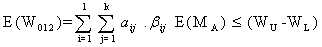 | (3.2.14) |
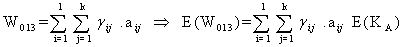 | (3.2.15) |
The constraint with respect to WBC loss count on malignant (stage-3) cells is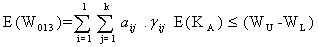 | (3.2.16) |
Putting (3.2.12), (3.2.14) and (3.16) together, the constraint with respect to the loss count of WBC is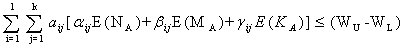 | (3.2.17) |
The constraints with minimum feasible eradicate Mutant (stage-I) cells in a tumor during drug administration at time‘t’ is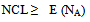 | (3.2.18) |
Similarly the constraints with Premalignant (stage-II) cell population at time t is 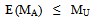 | (3.2.19) |
For Malignant (stage-III) cell population at time t is 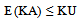 | (3.2.20) |
And the decision parameters are 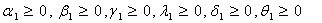 | (3.2.21) |
The resulting optimization problem for drug administration is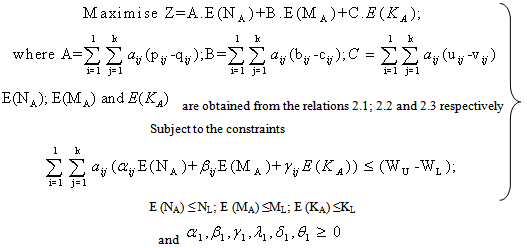 | (3.2.22) |
3.3. Programming Problem for Drug Vacation
As chemotherapy is a double-edged weapon in cancer treatment. It has its effect on the health of the patient during its administration as well as during its vacation also. Long time drug administration demands the recovery to the patient from the toxic exposure of the drug. This period will act as a stimulant to reactivate the natural immune system. The duration of drug absence should also be handled with optimal care for effective positive results in the process of chemotherapy. Hence there is a need of studying the optimal drug vacation.From the Notation and Terminology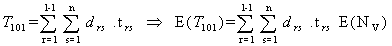 | (3.3.1) |
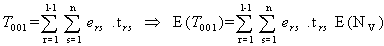 | (3.3.2) |
Which implies the net impact of drug vacation on one mutant (stage-I) cell is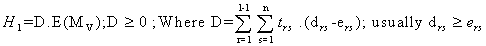 | (3.3.3) |
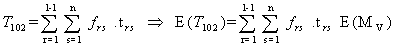 | (3.3.4) |
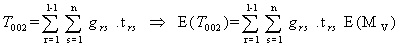 | (3.3.5) |
Which implies the net impact factor of drug vacation on a premalignant (stage-II) cell is 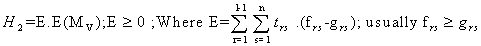 | (3.3.6) |
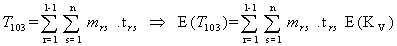 | (3.3.7) |
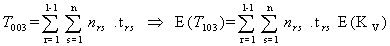 | (3.3.8) |
So as net impact of drug vacation on a malignant (stage-III) cell is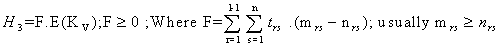 | (3.3.9) |
By considering 3.3.3, 3.3.6 and 3.3.9 the overall effect of drug vacation on all the 3 types of cell population is 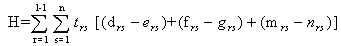 | (3.3.10) |
and H is to be maximized.Regarding the constraints of the problem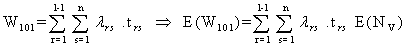 | (3.3.11) |
The constraint with respect to WBC loss count on mutant cells (Stage-I) is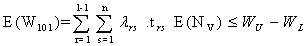 | (3.3.12) |
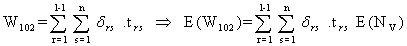 | (3.3.13) |
The constraint with respect to WBC loss count on premalignant cells (stage-II) is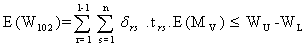 | (3.3.14) |
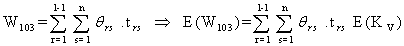 | (3.3.15) |
The constraint with respect to WBC loss count on malignant (stage-III) cells is 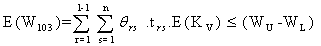 | (3.3.16) |
Putting (5.12), (5.14) and (5.16) together, the constraints with respect to the loss count of WBC is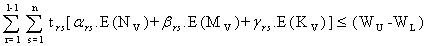 | (3.3.17) |
The constraint with mutant cell population during drug vacation at time‘t’ is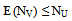 | (3.3.18) |
Similarly for premalignant cell population at time t is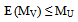 | (3.3.19) |
For malignant cells at time t is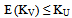 | (3.3.20) |
And the decision parameters are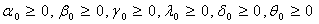 | (3.3.21) |
The resulting optimization problem for recovery of health during drug vacation is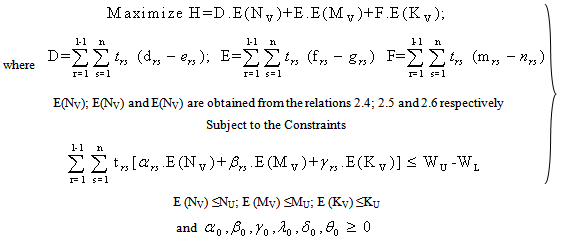 | (3.3.22) |
Table 4.1. For fixed values of t1=2; N0=7.6x107; M0=9.71x105; K0=9.8 x106; WU=5.5x106; WL=3.5x106; NU=1.5x105; NL=1.29x105; MU=11.5x105; ML=9.7x105; KU=1.2x106; KL= 10
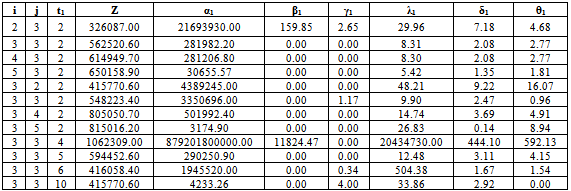 |
| |
|
Table 4.2. For fixed values of t1=2; N0=7.6x107; M0=9.71x105; K0=9.8 x106; WU=5.5x106; WL=3.5x106; NU=1.5x105; NL=1.29x105; MU=11.5x105; ML=9.7x105; KU=1.2x106; KL= 105
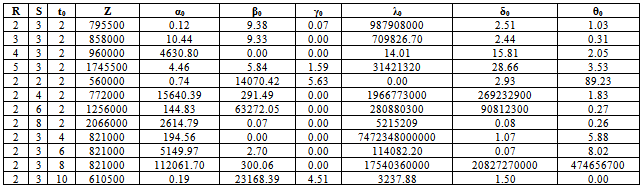 |
| |
|
4. Numerical Illustration & Sensitivity Analysis
In order to understand the model behaviour, a hypothetical data is considered. Decision parameters like growth, loss and transformation rates of cells among the 3stages, are obtained at different values of initial number of stage-1 cell (N0), Initial number of stage-2 cells (M0), and initial number of stage-3 cells (K0), WBC upper limit (WU), WBC lower limit (WL), lower and upper limits of stage-1 cells (NL,NU), lower and upper limits of stage-2 cells (ML,MU), lower and upper limits of stage-3 cells (KL,KU), etc. 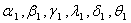 and
and 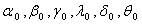 are obtained from the above non linear programming problems during drug administration and drug vacation for varying hypothetical values of i, j, r, s, t by using LINGO 8.0 and the results are presented in table – 4.1 and table-4.2.From the table 4.1 it is observed that Z (drug efficacy) is an increasing function of number of drug administration cycles and number of spells within the cycle when all other parameters are constant. It may indicate that increasing number of drug cycles and spells within a cycle will increase the drug efficacy. It is also observed that the parameters
are obtained from the above non linear programming problems during drug administration and drug vacation for varying hypothetical values of i, j, r, s, t by using LINGO 8.0 and the results are presented in table – 4.1 and table-4.2.From the table 4.1 it is observed that Z (drug efficacy) is an increasing function of number of drug administration cycles and number of spells within the cycle when all other parameters are constant. It may indicate that increasing number of drug cycles and spells within a cycle will increase the drug efficacy. It is also observed that the parameters 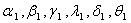 are decreasing functions of number of drug administration cycles. It may indicate that the increasing number of drug cycles will decrease the generation and transformation of the stage-I, stage-II and stage-III cells. It is also observed that the parameter
are decreasing functions of number of drug administration cycles. It may indicate that the increasing number of drug cycles will decrease the generation and transformation of the stage-I, stage-II and stage-III cells. It is also observed that the parameter 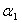 is decreasing function and
is decreasing function and 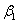 is invariant of change of number of spells within cycle. It may indicate that increasing number of spells within a cycle will decreases generation of stage-I cells and invariant of change of stage-II cells. It is further observed that Z is decreasing function of time ‘t’ when all other parameters are constant implies that longevity of drug administration above the required time may decrease drug efficacy. It is further observed that parameter
is invariant of change of number of spells within cycle. It may indicate that increasing number of spells within a cycle will decreases generation of stage-I cells and invariant of change of stage-II cells. It is further observed that Z is decreasing function of time ‘t’ when all other parameters are constant implies that longevity of drug administration above the required time may decrease drug efficacy. It is further observed that parameter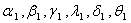 are decreasing functions and
are decreasing functions and 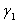 is increasing function of time ‘t’. It may be due to continuous drug administration will decrease the rate of generation of stage-I and stage-II cells but increase the transformation rate of stage-III cells from stage-II.From the table 4.2 it is observed that Z is an increasing function of number of DVP and number of days within the DVP when all other parameters are constant. It is also observed that
is increasing function of time ‘t’. It may be due to continuous drug administration will decrease the rate of generation of stage-I and stage-II cells but increase the transformation rate of stage-III cells from stage-II.From the table 4.2 it is observed that Z is an increasing function of number of DVP and number of days within the DVP when all other parameters are constant. It is also observed that 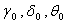 are increasing functions and
are increasing functions and 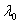 is decreasing function of number of DVP. It may indicate that increasing number of DVP during drug vacation will increase the transformation of stage-III from stage-II cells and death of stage-II and stage-III cells but decreases the death of stage-I cells. It is further observed that parameters
is decreasing function of number of DVP. It may indicate that increasing number of DVP during drug vacation will increase the transformation of stage-III from stage-II cells and death of stage-II and stage-III cells but decreases the death of stage-I cells. It is further observed that parameters 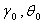 are decreasing function of number of days with in DVP. It may indicate that an increase of the number of days within DVP will decrease the transformation and death of stage-III cells. It is also observed that the Z is decreasing function of time when all other parameters are constant. It is further observed that
are decreasing function of number of days with in DVP. It may indicate that an increase of the number of days within DVP will decrease the transformation and death of stage-III cells. It is also observed that the Z is decreasing function of time when all other parameters are constant. It is further observed that 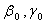 are increasing function,
are increasing function, 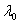 is decreasing function of time t. It may indicate that increasing the drug vacation time increases the generation of the stage-II and stage-III cell population.
is decreasing function of time t. It may indicate that increasing the drug vacation time increases the generation of the stage-II and stage-III cell population.
5. Summary and Conclusions
In cancer, chemotherapy the drug administration in spells with various quantities of mixed drugs. It is also to be implemented with drug vacation periods with various lengths of time units (say number of days). Either continuous and long spells drug administration or continuous long days of drug vacation are unwanted in a proper treatment of cancer. While developing the programming problem in two cases, during drug administration and during drug vacation separately, we have assumed that the behaviour of growth/loss of cancer cells and normal cells are complementary during these periods. Our study has explored the decision variables like threshold limits on drug administration times (minimum & maximum); duration of drug vacation periods, dosage level (quantum) of drug in each spell; number of cycles of drug administration; number of drug vacation spells; The times between two drug vacations and drug administration’s etc.
References
| [1] | P. Tirupathi Rao, BN Naveen Kumar, PRS Reddy (2013), “Three Stage Stochastic Modeling for Cancer Cell Growth under Chemotherapy”, International Journal of Advanced Computer and Mathematical Sciences, Vol4, Issue2, 2013, pp168-180 |
| [2] | Bahrami, K. and Kim, M., (1975) “Optimal control of multiplicative control system arising from cancer therapy”, IEEE. Trans. Auton., Control., 20,534-542. |
| [3] | Swan, G.W., (1977) “Some current mathematical topics in cancer research”, Edn. Univ. Microfilms. Inter, Ann Arbor |
| [4] | Ion C. Baianu (1986) , “Computer Models of Carcinogenesis and cancer chemotherapy optimization”, Mathematical Modeling , 7, PP 1513-1577. |
| [5] | Murray, J.M., (1990) “Some optimal control problems in cancer chemotherapy with toxicity limit “, Math. Biosci., 100, 49-67. |
| [6] | Murray, J.M., (1990) “Optimal control for a cancer chemotherapy”, Math. Biosci., Vol. 98, PP: 273- 287. |
| [7] | Martin , R.B., Fisher , M.E ., Minchen , R. F . and Teo , K.L., (1990) “ A mathematical model of cancer chemotherapy with an optimal selection of parameters “ , Math, Biosci, 99,205-230. |
| [8] | L.G.de Pillis and A.E. Radunskaya(2000) "A Model of Tumor Growth with Optimal Control", Argonne National Labs, Technical Report,. |
| [9] | Matreer, A.S. and Savkin, A. V. (2000), “Optimal Control applied to drug administration in cancer chemotherapy: the case of several toxicity constraints” Decision and Control, 2000. Proceedings of the 39 th IEEE Conference, 5, PP 4851, 4856. |
| [10] | Athanassios Iliadis Dominique Barbolosi (2000): Optimizing drug regimens in cancer chemotherapy by an efficacy — toxicity mathematical model Journal Computers and Biomedical Research archive Volume 33 Issue 3. |
| [11] | P. Tirupathi Rao, K. Srinivasa Rao & K. Padmalatha (2010) “Stochastic model for optimal drug administration in cancer chemotherapy”, International Journal of Engineering Science and Technology, 2(5), pp.859-865. |
| [12] | Dongning Li et. al (2010) “Optimal Catheter Placement for Chemotherapy”, Computer Aided Chemical Engineering, Volume 28, Pages 223-228 |
| [13] | P. Tirupathi Rao, D. Flora Evangel, K. Madhavi et.al (2012), “Stochastic Programming on Optimal Drug Administration for Two Stage Cancer Treatment Problem”, International Journal of Green Computing, Vol.3, No.1, pp: 1-10. |
| [14] | P. Tirupathi Rao, K.Madhavi, BN Naveen Kumar, PRS Reddy (2012), “Stochastic Modeling for Treatment Dependent Malignancy Growth”, International Journal of Advanced Scientific and Technical Research, Issue 2 Vol 4, PP 607-618 |
| [15] | K. Madhavi, P.Tirupathi Rao, PRS Reddy (2013), “Optimal Drug Administration for Cancer Chemotherapy through Stochastic Programming”, American Journal of Applied Mathematics and Mathematical Sciences, Vol.2, No.1, pp:35-45. |

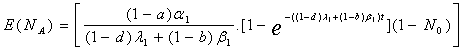
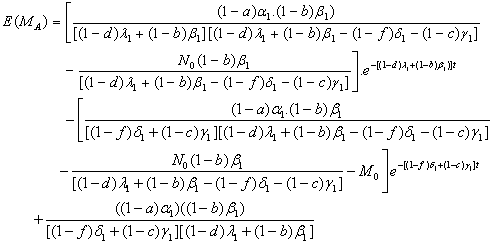
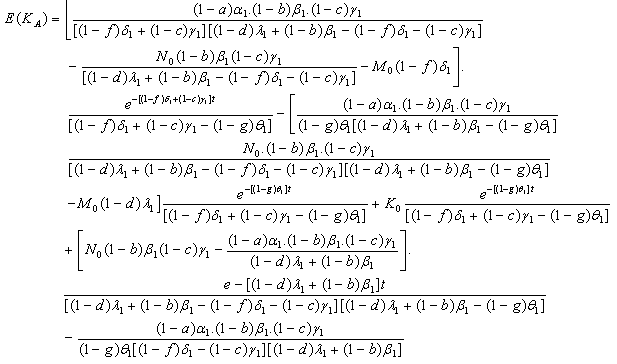
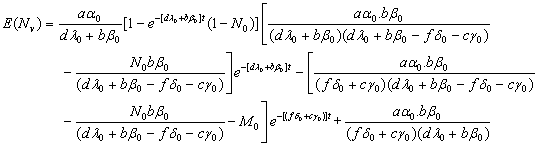
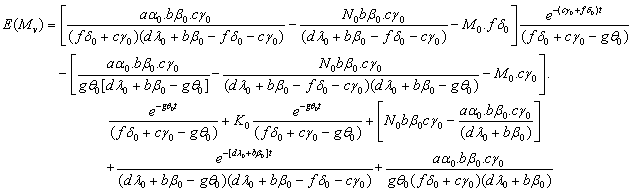
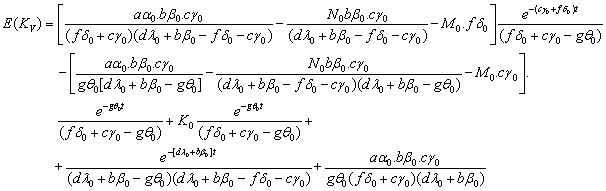

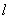 ;
;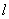 : Maximum number of drug cycles;j : Number of spells of drug administration in each cycle; j=1,2, …k; k : Maximum number of drug spells within a cycle; r : Number of drug vacation periods in the total treatment process; r=1,2, …
: Maximum number of drug cycles;j : Number of spells of drug administration in each cycle; j=1,2, …k; k : Maximum number of drug spells within a cycle; r : Number of drug vacation periods in the total treatment process; r=1,2, …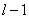 ; s : Number of days within a period of drug vacation; s=1,2, …
; s : Number of days within a period of drug vacation; s=1,2, …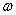 ;
;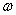 : Maximum number of days within a drug vacation period. aij: Number of units of drug doses in ith cycle and jth spell of drug administration (DA); pij : Positive (+ ve) effect of one unit DA on a mutant(stage-I) cell during ith cycle and jth spell; qij: Negative (- ve) effect of one unit DA on a mutant(stage-I)cell during ith cycle and jth spell; bij: +ve effect of one unit DA on a premalignant (stage-II) cell during ith cycle and jth spell; cij : -ve effect of one unit of DA on one premalignant (stage-II) cell during ith cycle and jth spell; uij : +ve effect of one unit DA on one malignant (stage-III) cell during ith cycle and jth spell; vij : - ve effect of one unit of DA on one malignant (stage-III) cell during ith cycle and jth spell; αij: Loss of WBC in one unit of DA for killing of one stage-I cell in ith cycle and jth spell; βij: Loss of WBC in one unit of DA for killing of one stage-II cell in ith cycle and jth spell; γij: Loss of WBC in one unit of DA for killing of one stage-III cell in ith cycle and jth spell;drs:+ve impact of one unit of drug vacation (DV) time on one "stage-I" cell in rth DV period, sth day; ers: - ve impact of one unit time of DV on one "stage-I" cell in rth DV period and sth day; frs: +ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; grs: - ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; mrs: +ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; nrs: - ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; λrs: Loss of WBC per unit time of DV due to growth of one "stage-I" cell in rth DV period, sth day; δrs: Loss of WBC per unit time of DV due to growth of one "stage-II" cell in rth DV perood, sth day; θrs: Loss of WBC per unit time of DV due to growth of one "stage-III" cell in rth DV period, sth day; trs : The number of time units in rth DV Period and sth day ; for r = 1,2, …; s = 1,2,….n Tx,y,z: Total +ve /-ve (x) effect of treatment during drug presence/absence(y) while targeting the Mutant/ Premalignant/ Malignant (z) cell population.Where x=1: If drug has positive effectiveness; x =0: If drug has negative effectivenessy=1: If Drug is present; y=0: If Drug is absentz=1: If the cell is in "stage-1" ; z=2: If the cell is in "stage-2"; z=3: If the cell is in "stage-3";WX,Y,Z: Total loss/growth(X) of WBC during drug presence/absence(Y) while targeting to destroy Mutant/ Premalignant/Malignant (Z) cell population.Where X=1: If there is Growth of WBC; X =0: If there is Loss of WBCY=1: During Drug Presence; Y=0: During Drug AbsenceZ=1: For Mutant cell; Z=2: For Premalignant cell; Z=3: For Malignant cellWU, WL: The desired optimal upper & lower limits of healthy sizes of WBC during treatment. NU, NL : The critical target upper & lower limits on size of the mutant (stage-I) cells MU, ML: The critical target limit upper & lower limits on size of the premalignant (stage-II) cells.KU, KL : The critical target upper and lower limits on size of the malignant (stage-III) cells
: Maximum number of days within a drug vacation period. aij: Number of units of drug doses in ith cycle and jth spell of drug administration (DA); pij : Positive (+ ve) effect of one unit DA on a mutant(stage-I) cell during ith cycle and jth spell; qij: Negative (- ve) effect of one unit DA on a mutant(stage-I)cell during ith cycle and jth spell; bij: +ve effect of one unit DA on a premalignant (stage-II) cell during ith cycle and jth spell; cij : -ve effect of one unit of DA on one premalignant (stage-II) cell during ith cycle and jth spell; uij : +ve effect of one unit DA on one malignant (stage-III) cell during ith cycle and jth spell; vij : - ve effect of one unit of DA on one malignant (stage-III) cell during ith cycle and jth spell; αij: Loss of WBC in one unit of DA for killing of one stage-I cell in ith cycle and jth spell; βij: Loss of WBC in one unit of DA for killing of one stage-II cell in ith cycle and jth spell; γij: Loss of WBC in one unit of DA for killing of one stage-III cell in ith cycle and jth spell;drs:+ve impact of one unit of drug vacation (DV) time on one "stage-I" cell in rth DV period, sth day; ers: - ve impact of one unit time of DV on one "stage-I" cell in rth DV period and sth day; frs: +ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; grs: - ve impact of one unit time of DV on one "stage-II" cell during rth DV period and sth day; mrs: +ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; nrs: - ve impact of one unit time of DV on one "stage-III" cell during rth DV period and sth day; λrs: Loss of WBC per unit time of DV due to growth of one "stage-I" cell in rth DV period, sth day; δrs: Loss of WBC per unit time of DV due to growth of one "stage-II" cell in rth DV perood, sth day; θrs: Loss of WBC per unit time of DV due to growth of one "stage-III" cell in rth DV period, sth day; trs : The number of time units in rth DV Period and sth day ; for r = 1,2, …; s = 1,2,….n Tx,y,z: Total +ve /-ve (x) effect of treatment during drug presence/absence(y) while targeting the Mutant/ Premalignant/ Malignant (z) cell population.Where x=1: If drug has positive effectiveness; x =0: If drug has negative effectivenessy=1: If Drug is present; y=0: If Drug is absentz=1: If the cell is in "stage-1" ; z=2: If the cell is in "stage-2"; z=3: If the cell is in "stage-3";WX,Y,Z: Total loss/growth(X) of WBC during drug presence/absence(Y) while targeting to destroy Mutant/ Premalignant/Malignant (Z) cell population.Where X=1: If there is Growth of WBC; X =0: If there is Loss of WBCY=1: During Drug Presence; Y=0: During Drug AbsenceZ=1: For Mutant cell; Z=2: For Premalignant cell; Z=3: For Malignant cellWU, WL: The desired optimal upper & lower limits of healthy sizes of WBC during treatment. NU, NL : The critical target upper & lower limits on size of the mutant (stage-I) cells MU, ML: The critical target limit upper & lower limits on size of the premalignant (stage-II) cells.KU, KL : The critical target upper and lower limits on size of the malignant (stage-III) cells 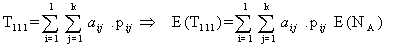
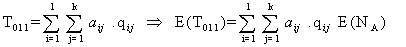
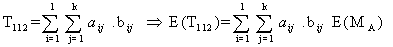
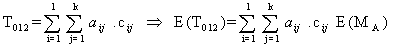
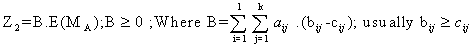
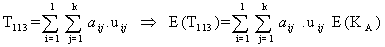
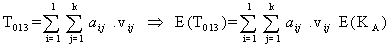
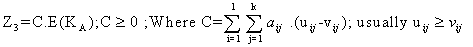
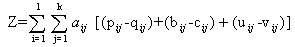
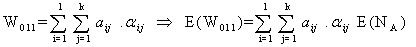
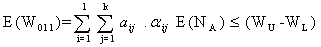
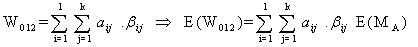
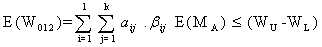
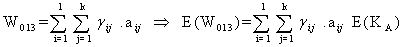
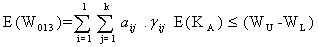
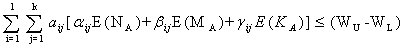
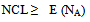
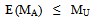
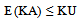
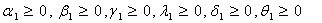
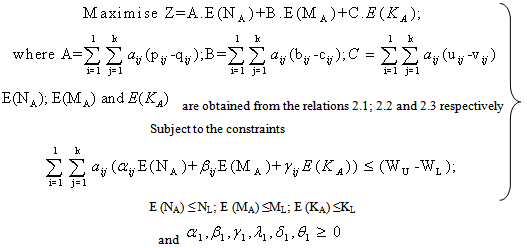
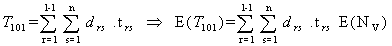
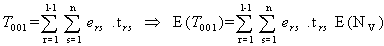
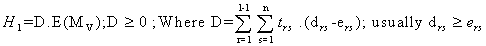
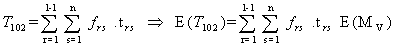
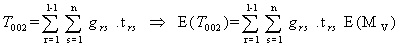
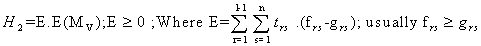
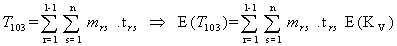
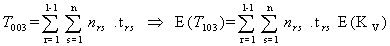
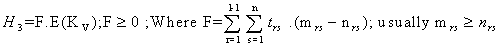
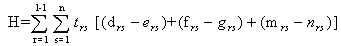
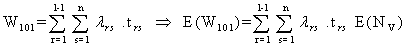
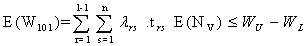
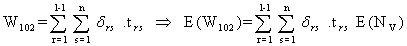
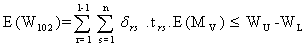
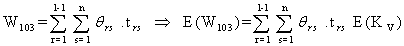
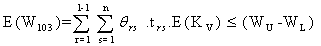
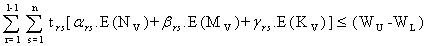
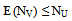
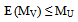
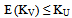
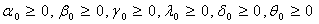
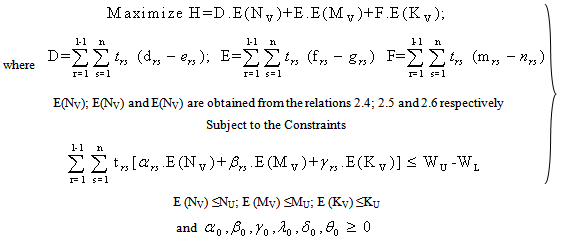
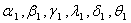 and
and 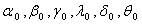 are obtained from the above non linear programming problems during drug administration and drug vacation for varying hypothetical values of i, j, r, s, t by using LINGO 8.0 and the results are presented in table – 4.1 and table-4.2.From the table 4.1 it is observed that Z (drug efficacy) is an increasing function of number of drug administration cycles and number of spells within the cycle when all other parameters are constant. It may indicate that increasing number of drug cycles and spells within a cycle will increase the drug efficacy. It is also observed that the parameters
are obtained from the above non linear programming problems during drug administration and drug vacation for varying hypothetical values of i, j, r, s, t by using LINGO 8.0 and the results are presented in table – 4.1 and table-4.2.From the table 4.1 it is observed that Z (drug efficacy) is an increasing function of number of drug administration cycles and number of spells within the cycle when all other parameters are constant. It may indicate that increasing number of drug cycles and spells within a cycle will increase the drug efficacy. It is also observed that the parameters 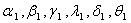 are decreasing functions of number of drug administration cycles. It may indicate that the increasing number of drug cycles will decrease the generation and transformation of the stage-I, stage-II and stage-III cells. It is also observed that the parameter
are decreasing functions of number of drug administration cycles. It may indicate that the increasing number of drug cycles will decrease the generation and transformation of the stage-I, stage-II and stage-III cells. It is also observed that the parameter 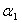 is decreasing function and
is decreasing function and 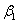 is invariant of change of number of spells within cycle. It may indicate that increasing number of spells within a cycle will decreases generation of stage-I cells and invariant of change of stage-II cells. It is further observed that Z is decreasing function of time ‘t’ when all other parameters are constant implies that longevity of drug administration above the required time may decrease drug efficacy. It is further observed that parameter
is invariant of change of number of spells within cycle. It may indicate that increasing number of spells within a cycle will decreases generation of stage-I cells and invariant of change of stage-II cells. It is further observed that Z is decreasing function of time ‘t’ when all other parameters are constant implies that longevity of drug administration above the required time may decrease drug efficacy. It is further observed that parameter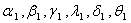 are decreasing functions and
are decreasing functions and 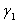 is increasing function of time ‘t’. It may be due to continuous drug administration will decrease the rate of generation of stage-I and stage-II cells but increase the transformation rate of stage-III cells from stage-II.From the table 4.2 it is observed that Z is an increasing function of number of DVP and number of days within the DVP when all other parameters are constant. It is also observed that
is increasing function of time ‘t’. It may be due to continuous drug administration will decrease the rate of generation of stage-I and stage-II cells but increase the transformation rate of stage-III cells from stage-II.From the table 4.2 it is observed that Z is an increasing function of number of DVP and number of days within the DVP when all other parameters are constant. It is also observed that 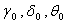 are increasing functions and
are increasing functions and 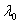 is decreasing function of number of DVP. It may indicate that increasing number of DVP during drug vacation will increase the transformation of stage-III from stage-II cells and death of stage-II and stage-III cells but decreases the death of stage-I cells. It is further observed that parameters
is decreasing function of number of DVP. It may indicate that increasing number of DVP during drug vacation will increase the transformation of stage-III from stage-II cells and death of stage-II and stage-III cells but decreases the death of stage-I cells. It is further observed that parameters 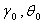 are decreasing function of number of days with in DVP. It may indicate that an increase of the number of days within DVP will decrease the transformation and death of stage-III cells. It is also observed that the Z is decreasing function of time when all other parameters are constant. It is further observed that
are decreasing function of number of days with in DVP. It may indicate that an increase of the number of days within DVP will decrease the transformation and death of stage-III cells. It is also observed that the Z is decreasing function of time when all other parameters are constant. It is further observed that 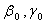 are increasing function,
are increasing function, 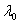 is decreasing function of time t. It may indicate that increasing the drug vacation time increases the generation of the stage-II and stage-III cell population.
is decreasing function of time t. It may indicate that increasing the drug vacation time increases the generation of the stage-II and stage-III cell population. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
