Ilgar G. Mamedov
A. I. Huseynov Institute of Cybernetics of NAS of Azerbaijan. Az 1141, Azerbaijan, Baku st. B. Vahabzade, 9
Correspondence to: Ilgar G. Mamedov, A. I. Huseynov Institute of Cybernetics of NAS of Azerbaijan. Az 1141, Azerbaijan, Baku st. B. Vahabzade, 9.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In the paper, the considered equation as a pseudoparabolic equation generalizes not only classic equations of mathematical physics (heat-conductivity equations, string vibration equation) and also many models differential equations (telegraph equation, Aller's equation , moisture transfer generalized equation, Manjeron equation, Boussinesq-Lyav equation and etc.). For this pseudoparabolic differential equation of sixth order with discontinuous coefficients we consider a problem with conditions on all the boundary. As a non-local problem this problem by its statement plays an intermediate role between the problems with boundary conditions of first kind (i.e. Dirichlet problems) and second kind(i.e. Neumann problems) and differs from them. Furthermore, it is easy to see that by its statement this non-local problem doesn't coincide with the third boundary value problems and very differs from these problems. It is grounded that the boundary condition on all the boundary in the classic and non-classic treatment are equivalent to each other, and such boundary conditions are demonstrated in geometric form. Even from geometric interpretation can see that the grounded non-classic treatment doesn't require any additional conditions of agreement type. Thus, namely in this paper, the non-classic problem with conditions on all the boundary is grounded for a pseudoparabolic equation of sixth order. For simplicity, this was demonstrated for one model case in one of S.L. Sobolev's isotropic space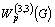 .
.
Keywords:
Non-local Boundary Problem, a Problem with Conditions on all the Boundary, Pseudoparapolic Equation, Discontinuous Coefficients Equations
Cite this paper: Ilgar G. Mamedov, On a Problem with Conditions on All Boundary for a Pseudoparabolic Equation, American Journal of Operational Research, Vol. 3 No. 2, 2013, pp. 51-56. doi: 10.5923/j.ajor.20130302.04.
1. Introduction
Urgency of investigations conducted in this field is explained by appearance of local and non-local problems for discontinuous coefficients equations connected with different applied problems. Such type problems arise for example, while studying the problems of moisture, transfer in soils, heat transfer in heterogeneous media, diffusion of thermal neutrons in inhibitors, simulation of different biological processes, phenomena and etc[1-7].Pseudoparabolic equations are attracted for sufficiently adequate description of a great deal of real processes occurring in the nature, engineering and etc. In particular, many processes arising in the theory of fluid filtration in cracked media are described by discontinuous coefficient pseudoparabolic equations [8-9]. Therewith, the important principal moment is that the considered equation possesses discontinuous coefficients that satisfy only some 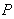 -integrability and boundednes conditions, i.e. the considered pseudoparabolic differential operator has no traditional adjoint operator. Therefore, the Riemann function for such an equation can’t be investigated by the classic method of characteristics. It should be specially noted that up to now in references, it was succeeded to construct the Riemann function for different classes of equations only for the case of sufficiently smooth coefficients.In the present paper, here consider characteristic problem with conditions, setting on all boundary, in two order space for sixth order equation with discontinuous coefficients. The coefficients in this pseudoparabolic equation are not necessarily differentiable; therefore, there does not exist a formally adjoint differential equation making a certain sense. For this reason, this question cannot be investigated by the well-known methods using classical integration by parts and Riemann functions or classical-type fundamental solutions. The theme of the present paper, devoted to the investigation of boundary-value problems for sixth order differential equations of pseudoparabolic type, according to the above-stated is very actual for the solution of theoretical and practical problems. From this point of view, the paper is devoted to the actual problems of mathematical physics and operational research.
-integrability and boundednes conditions, i.e. the considered pseudoparabolic differential operator has no traditional adjoint operator. Therefore, the Riemann function for such an equation can’t be investigated by the classic method of characteristics. It should be specially noted that up to now in references, it was succeeded to construct the Riemann function for different classes of equations only for the case of sufficiently smooth coefficients.In the present paper, here consider characteristic problem with conditions, setting on all boundary, in two order space for sixth order equation with discontinuous coefficients. The coefficients in this pseudoparabolic equation are not necessarily differentiable; therefore, there does not exist a formally adjoint differential equation making a certain sense. For this reason, this question cannot be investigated by the well-known methods using classical integration by parts and Riemann functions or classical-type fundamental solutions. The theme of the present paper, devoted to the investigation of boundary-value problems for sixth order differential equations of pseudoparabolic type, according to the above-stated is very actual for the solution of theoretical and practical problems. From this point of view, the paper is devoted to the actual problems of mathematical physics and operational research.
2. Problem Statement
Consider the equation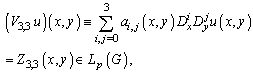 | (1) |
where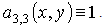 Here
Here 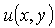 is a desired function defined on
is a desired function defined on ;
; 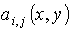 are the given measurable function on
are the given measurable function on , where
, where 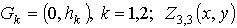 is a given measurable function on
is a given measurable function on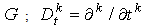 is a generalized differentiation operator in S.L.Sobolev sense
is a generalized differentiation operator in S.L.Sobolev sense 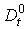 is an identity transformation operator.Equation (1) is a hyperbolic equation possessing two real characteristics
is an identity transformation operator.Equation (1) is a hyperbolic equation possessing two real characteristics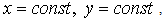 the first and second of which is three-fold. Therefore, in some sense we can consider equation (1) as a pseudoparabolic equation [10]. This equation is a generalization of the equation of thin spherical shell bending [11. p. 258].In this paper we consider equation (1) in the general case when the coefficients
the first and second of which is three-fold. Therefore, in some sense we can consider equation (1) as a pseudoparabolic equation [10]. This equation is a generalization of the equation of thin spherical shell bending [11. p. 258].In this paper we consider equation (1) in the general case when the coefficients 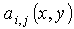 are non-smooth functions satisfying only the conditions:
are non-smooth functions satisfying only the conditions: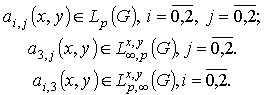 There with the important principal moment is that the equation under consideretion possesses discontinuous coefficients that satisfy only some
There with the important principal moment is that the equation under consideretion possesses discontinuous coefficients that satisfy only some 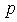 -integrability and boundedness conditions, i.e. the considered differentional operator
-integrability and boundedness conditions, i.e. the considered differentional operator 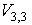 has no traditional conjugated operator.Under this conditions, the solution
has no traditional conjugated operator.Under this conditions, the solution 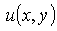 of equation (1) will be sought in S.L.Sobolev space
of equation (1) will be sought in S.L.Sobolev space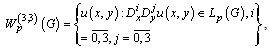 ,where
,where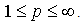 We'll define the norm in the isotropic space
We'll define the norm in the isotropic space  by the equality
by the equality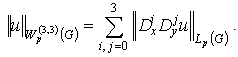
2.1. Problem Statement in Classical Form
We can give the classic form conditions on all the boundary for equation (1) as follows [12]: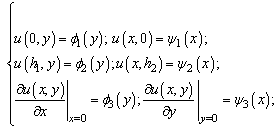 | (2) |
where 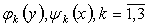 are the given measurable functions on
are the given measurable functions on Obviously, in the case of conditions (2) in addition to conditions
Obviously, in the case of conditions (2) in addition to conditions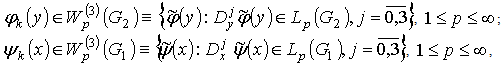 the given functions satisfy also the following agreement conditions (see. Fig. 1):
the given functions satisfy also the following agreement conditions (see. Fig. 1):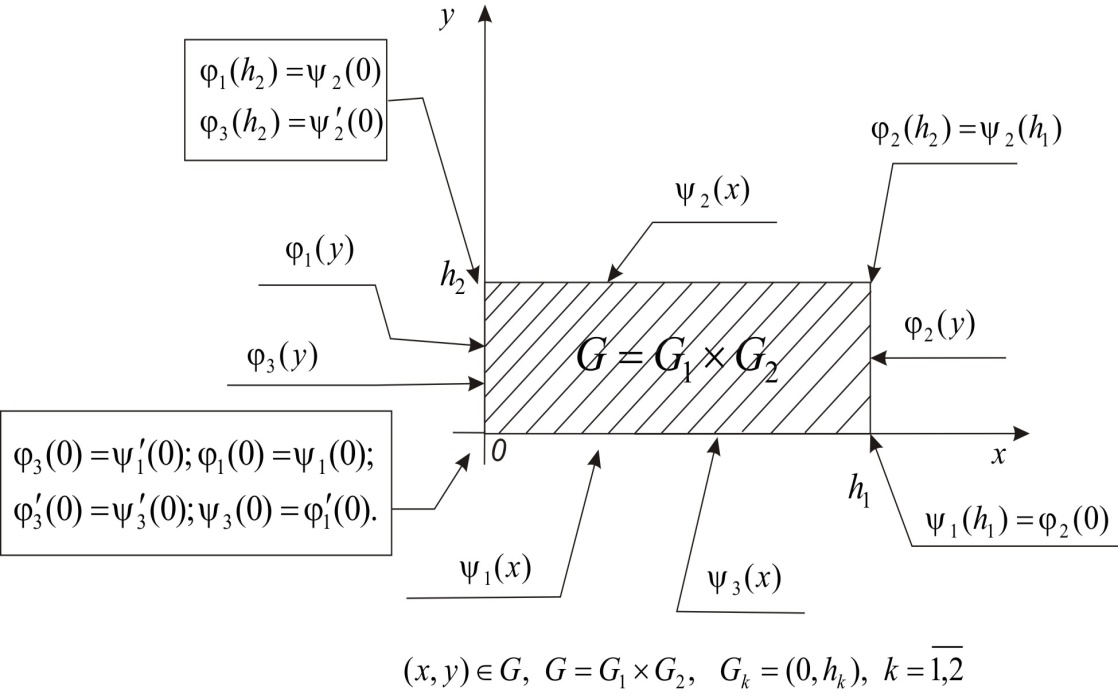 | Figure 1. Geometric interpretation of classical conditions on all the boundary |
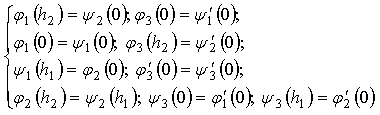 | (3) |
Obviously, conditions (2) are close to boundary conditions of the Dirichlet problem from [13].
2.2. Problem Statement in Non-classical Treatment
Consider the following non-classical boundary conditions: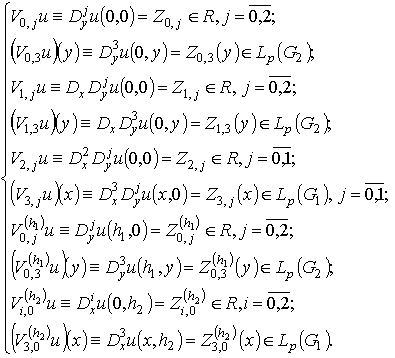 | (4) |
3. Methodology
The Riemann’s method does not work for differential equations with discontinuous coefficients.In the present paper, a method that essentially uses modern methods of the theory of functions and functional analysis is worked out for investigations of such problems. In the main, this method it requested in conformity to pseudoparabolic equations of sixth order with triple characteristics. Notice that, in this paper the considered equation is a generation of many model equations of some processes (for example, generalized equations of moisture transfer, telegraph equations, string vibrations equations and etc).
3.1. Method Agreement Conditions
If the function 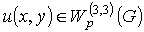 is a solution of the classical form problem (1), (2), with conditions on all the boundary then it is also a solution of problem (1),(4) for
is a solution of the classical form problem (1), (2), with conditions on all the boundary then it is also a solution of problem (1),(4) for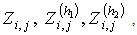 determined by the following equalities:
determined by the following equalities: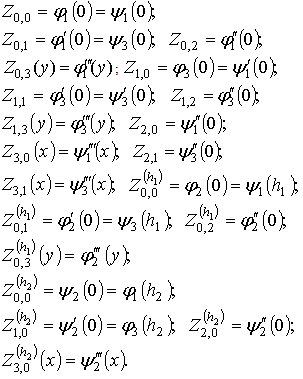
3.2. Method Integral Representation
It is easy to prove that the inverse one is also true. In other words, if the function 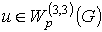 is a solution of problem (1), (4) (see. Fig. 2), then it is also a solution of problem (1), (2) for the following functions:
is a solution of problem (1), (4) (see. Fig. 2), then it is also a solution of problem (1), (2) for the following functions: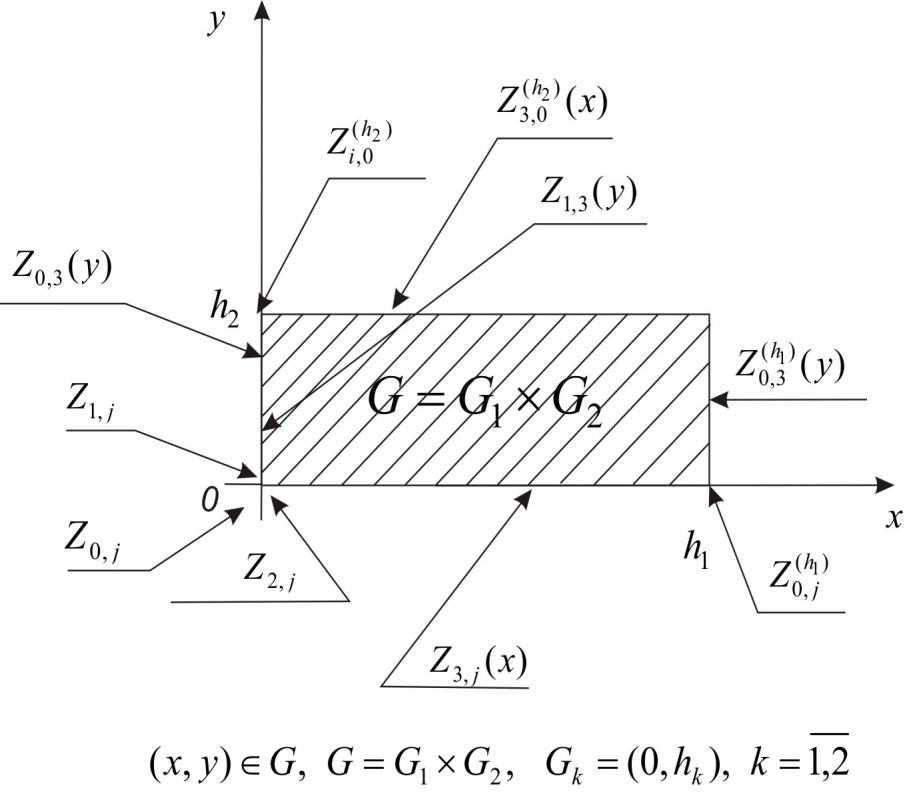 | Figure 2. Geometrical interpretation of conditions on all the boundary in non-classical treatment |
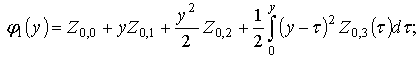 | (5) |
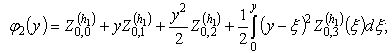 | (6) |
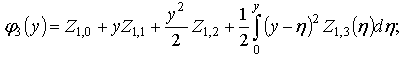 | (7) |
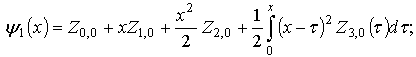 | (8) |
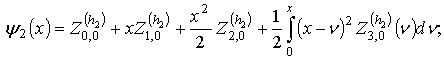 | (9) |
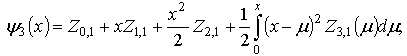 | (10) |
Note that the functions (5)-(10) possess one important property, more exactly, agreement condition (3) for all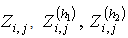 having the above-stated properties are fulfilled for them automatically. Therefore equalities (5)-(10) may be considered as a general form of all the functions
having the above-stated properties are fulfilled for them automatically. Therefore equalities (5)-(10) may be considered as a general form of all the functions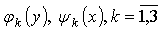 , satisfying agreement conditions (3).
, satisfying agreement conditions (3).
4. Result
So, classic type problems (1), (2) and of the form (1), (4) with conditions on all the boundary are equivalent in general case. However, the non - classic problem (1), (4) with conditions on the boundary is more natural by statement than problem (1), (2).This is connected with the fact that in the statement of problem (1), (4) with conditions on all the boundary, the right parts of boundary conditions don't require additional conditions of agreement type. Note that various boundary value problems with non classic conditions not requiring agreement conditions were substantiated in the author's papers [14-15].
5. Discussion and Conclusions
In the paper a non-classical type boundary problem is substantiated for a pseudoparabolic equation with non-smooth coefficients and with a sixth order dominating derivative. Classic boundary conditions are reduced to non-classic conditions by means of integral representations. Such statement of the problem has several advantages: 1) No additional agreement conditions are required in this statement;2) One can consider this statement as a problem formulated in terms of traces in the Sobolev space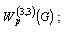 3) In this statement the considered equation is a generalization of many model equations of some processes (e.g. moisture transfer equation, telegraph equation, string vibration equations and etc.).
3) In this statement the considered equation is a generalization of many model equations of some processes (e.g. moisture transfer equation, telegraph equation, string vibration equations and etc.).
References
| [1] | Nakhushev A.M., Equations of Mathematical Biology, Moscow, 1995, 301 pp. ( in Russian) |
| [2] | Akhiev S. S. Fundamental solutions of some local and nonlocal boundary value problems and their representations. Dokl. Akad. Nauk SSSR, 271:2 (1983), 265–269 (in Russian). |
| [3] | Oruço˘glu K. and Akhiev S. S. The Riemann function for the third-order one-dimensional pseudoparabolic equation, Acta Appl. Math. 53:3 (1998), 353–370. |
| [4] | Kozhanov A.I. On a non-local boundary value problem with variable coefficients for heat-conductvity and Aller equations. Diff. Uravn. 40:6 (2004), 763-764. (in Russian) |
| [5] | Dzhokhadze O.M. On the three-dimensional generalized Goursat problem for a third-order equation, and related general two-dimensional Volterra integral equations of the first kind. Differ. Equat., 42:3 (2006), 412–421. |
| [6] | Mamedov I.G. The study of the problem with integro-multipoint boundary conditions for the generalized equation of moisture transfer. Izv. NAN Azerb. Ser. Fiz.-Tekhn. Matem. Nauk, 27:2–3 (2007),121–126 (in Russian) |
| [7] | Mamedov I.G. Optimal control problem in processes described by a non-local problem with loadings for a hyperbolic integro-differential equation. Izv. NAN Azerb. Ser. Fiz.-Tekhn. Matem. Nauk, 24:2 (2004), 74-79. (in Russian) |
| [8] | Mamedov I.G. A mixed problem with nonlocal boundary conditions of Bitsadze–Samarskiy and Samarskiy–Ionkin types that arises in modeling the filtration of a fluid in fractured media. Izv.NAN Azerb. Ser. Fiz.-Tekhn. Matem. Nauk , 26:3 (2006), 32–37(in Russian) |
| [9] | Mamedov I.G. A fundamental solution to the Cauchy problem for a fourth-order pseudoparabolic equation. Computational Mathematics and Mathematical Physics. 49:1 (2009), 93-104. |
| [10] | Soldatov A.P. , Shkhanukov M.Kh. Boundary value problems with A.A.Samarsky general non-local conditions of higher order pseudo-parabolic equations. DAN SSSR, 297:3 (1987), 547-552.(in Russian) |
| [11] | I.N.Vekua, New solution methods of elliptic equations M.: L.Gostechized, 1948. 296 pp. (in Russian) |
| [12] | Utkina E.A. A problem with conditions on all the boundary for a sixth order pseudoparabolic equation. Izv. Saratovskogo Univer. Ser. Matem. i Mekhan., Informatika, 11:2 (2011), 36-41. (in Russian) |
| [13] | Utkina E.A. Dirichlet problem for a fourth order equation. Differ. Uravn. 47:4 (2011), 600-604. (in Russian) |
| [14] | Mamedov I.G. Fundamental solution of initial-boundary value problem for fourth-order pseudoparabolic equations with nonsmooth coefficients. Vladikavkaz. Mat. Zh., 12:1 (2010), 17–32. (in Russian) |
| [15] | Mamedov I.G. Three-dimensional integro-multipoint boundary value problem for loaded Volterra-hyperbolic integro-differential equations of Bianchi type . Vestn. Samar. Gos. Tekhn. Univ. Ser. Fiz.-Mat. Nauki, 1:26 (2012), 8-20. (in Russian). |

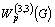 .
.
 -integrability and boundednes conditions, i.e. the considered pseudoparabolic differential operator has no traditional adjoint operator. Therefore, the Riemann function for such an equation can’t be investigated by the classic method of characteristics. It should be specially noted that up to now in references, it was succeeded to construct the Riemann function for different classes of equations only for the case of sufficiently smooth coefficients.In the present paper, here consider characteristic problem with conditions, setting on all boundary, in two order space for sixth order equation with discontinuous coefficients. The coefficients in this pseudoparabolic equation are not necessarily differentiable; therefore, there does not exist a formally adjoint differential equation making a certain sense. For this reason, this question cannot be investigated by the well-known methods using classical integration by parts and Riemann functions or classical-type fundamental solutions. The theme of the present paper, devoted to the investigation of boundary-value problems for sixth order differential equations of pseudoparabolic type, according to the above-stated is very actual for the solution of theoretical and practical problems. From this point of view, the paper is devoted to the actual problems of mathematical physics and operational research.
-integrability and boundednes conditions, i.e. the considered pseudoparabolic differential operator has no traditional adjoint operator. Therefore, the Riemann function for such an equation can’t be investigated by the classic method of characteristics. It should be specially noted that up to now in references, it was succeeded to construct the Riemann function for different classes of equations only for the case of sufficiently smooth coefficients.In the present paper, here consider characteristic problem with conditions, setting on all boundary, in two order space for sixth order equation with discontinuous coefficients. The coefficients in this pseudoparabolic equation are not necessarily differentiable; therefore, there does not exist a formally adjoint differential equation making a certain sense. For this reason, this question cannot be investigated by the well-known methods using classical integration by parts and Riemann functions or classical-type fundamental solutions. The theme of the present paper, devoted to the investigation of boundary-value problems for sixth order differential equations of pseudoparabolic type, according to the above-stated is very actual for the solution of theoretical and practical problems. From this point of view, the paper is devoted to the actual problems of mathematical physics and operational research.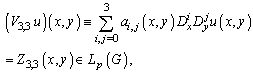
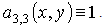 Here
Here 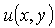 is a desired function defined on
is a desired function defined on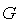 ;
; 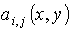 are the given measurable function on
are the given measurable function on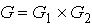 , where
, where 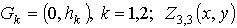 is a given measurable function on
is a given measurable function on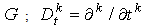 is a generalized differentiation operator in S.L.Sobolev sense
is a generalized differentiation operator in S.L.Sobolev sense 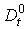 is an identity transformation operator.Equation (1) is a hyperbolic equation possessing two real characteristics
is an identity transformation operator.Equation (1) is a hyperbolic equation possessing two real characteristics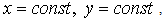 the first and second of which is three-fold. Therefore, in some sense we can consider equation (1) as a pseudoparabolic equation [10]. This equation is a generalization of the equation of thin spherical shell bending [11. p. 258].In this paper we consider equation (1) in the general case when the coefficients
the first and second of which is three-fold. Therefore, in some sense we can consider equation (1) as a pseudoparabolic equation [10]. This equation is a generalization of the equation of thin spherical shell bending [11. p. 258].In this paper we consider equation (1) in the general case when the coefficients 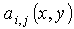 are non-smooth functions satisfying only the conditions:
are non-smooth functions satisfying only the conditions: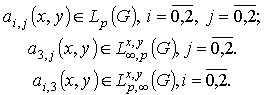 There with the important principal moment is that the equation under consideretion possesses discontinuous coefficients that satisfy only some
There with the important principal moment is that the equation under consideretion possesses discontinuous coefficients that satisfy only some 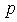 -integrability and boundedness conditions, i.e. the considered differentional operator
-integrability and boundedness conditions, i.e. the considered differentional operator 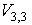 has no traditional conjugated operator.Under this conditions, the solution
has no traditional conjugated operator.Under this conditions, the solution 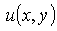 of equation (1) will be sought in S.L.Sobolev space
of equation (1) will be sought in S.L.Sobolev space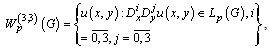 ,where
,where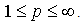 We'll define the norm in the isotropic space
We'll define the norm in the isotropic space 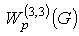 by the equality
by the equality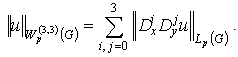
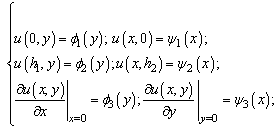
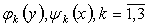 are the given measurable functions on
are the given measurable functions on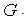 Obviously, in the case of conditions (2) in addition to conditions
Obviously, in the case of conditions (2) in addition to conditions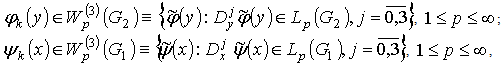 the given functions satisfy also the following agreement conditions (see. Fig. 1):
the given functions satisfy also the following agreement conditions (see. Fig. 1):
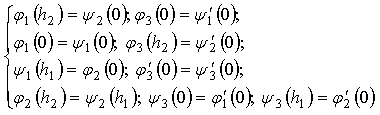
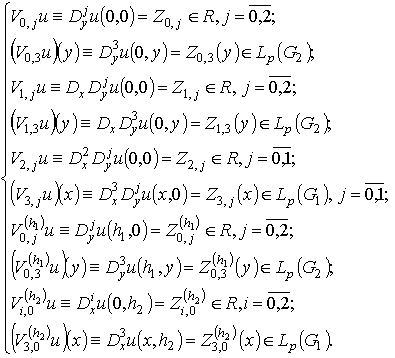
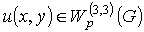 is a solution of the classical form problem (1), (2), with conditions on all the boundary then it is also a solution of problem (1),(4) for
is a solution of the classical form problem (1), (2), with conditions on all the boundary then it is also a solution of problem (1),(4) for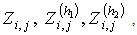 determined by the following equalities:
determined by the following equalities: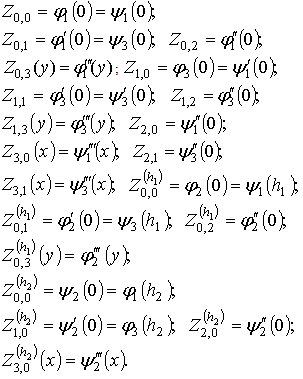
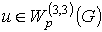 is a solution of problem (1), (4) (see. Fig. 2), then it is also a solution of problem (1), (2) for the following functions:
is a solution of problem (1), (4) (see. Fig. 2), then it is also a solution of problem (1), (2) for the following functions:
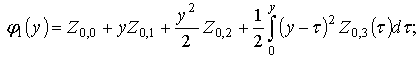
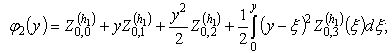
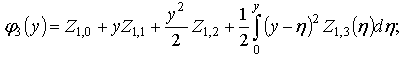
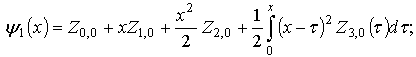
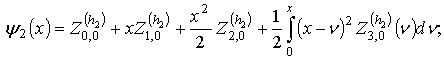
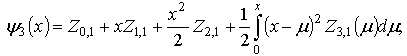
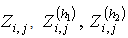 having the above-stated properties are fulfilled for them automatically. Therefore equalities (5)-(10) may be considered as a general form of all the functions
having the above-stated properties are fulfilled for them automatically. Therefore equalities (5)-(10) may be considered as a general form of all the functions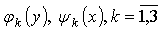 , satisfying agreement conditions (3).
, satisfying agreement conditions (3).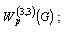 3) In this statement the considered equation is a generalization of many model equations of some processes (e.g. moisture transfer equation, telegraph equation, string vibration equations and etc.).
3) In this statement the considered equation is a generalization of many model equations of some processes (e.g. moisture transfer equation, telegraph equation, string vibration equations and etc.).  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML