1. Introduction

A supply chain consists of all parties involved, directly or indirectly fulfilling customer request. The supply chain includes not only the manufacturer and suppliers, but also transporters, warehouses, retailers and even customers. Within each organization, such as a manufacturer, the supply chain includes all functions involved in receiving and filling a customer request. These functions include but are not limited to new product development, marketing, operations, distribution, finance, and customer service. A supply chain is a sequence of processes and flows that take place within and between different stages and combine to fill a customer need for a product. In this study the replenishment cycle is used only which consists of the relationship between retailer and warehouse. The major goal of every supply chain is to maximize its profit. But in most supply chain the main target of each stage is to maximize its own profit rather than total profit and this is the main theme of decentralized decision. But in centralized decisions all the stages try to increase the total supply chain profitability. Many researches are done for single item order quantity in centralized and decentralized decisions. To reduce the lot size effectively, the source of the fixed cost must be identified. One major source of fixed costs is transportation. In several companies the array of products sold is divided into families or groups, with each group managed independently. This results in separate orders and deliveries for each product family, thus lowering the overall cycle inventory. Aggregating orders and deliveries across product families is an effective mechanism to lower cycle inventories. When considering fixed costs, one cannot ignore the receiving or loading costs. As more products are included in a single order the product variety on a truck increases. The receiving warehouse now has to update inventory records for more items per truck. In addition, the tasks of putting inventory into storage now become more expensive because each distinct item must be stocked in a separate location. Thus when attempting to reduce lot sizes it is important to focus on reducing these costs.

In the course of globalization, many enterprises change their strategies and are coupled in partnerships with suppliers, subcontractors and customers. Production planning in a supply chain is a complicated and difficult task, as it has to be optimal both for the local manufacturing units and for the whole supply chain network. Different researchers have provided models and algorithms for single-item order quantity both in centralized and decentralized cases[3],[5]. This paper represents an extension of related works found in literatures taking in account the order quantity of multi-items for a warehouse–retailer supply chain where the demands of retailer are known. This order quantity is determined by considering that all products are ordered and received jointly. So transportation cost from warehouse to retailer will be the multiplication of number of orders and transportation cost per order. Models are developed to minimize the total system cost in case of both decentralized and centralized decisions.

The organization of the paper is as follows: section 2 comprises the review of related literatures; section 3 presents the formulation of the models for both centralized and decentralized case; section 4 presents the algorithm for centralized decision; a case study is carried out in section 5; numerical results are discussed in section 6 and section 7 summarises the conclusions of the paper.

2. Literature Review

Some researchers like Axsäter ([1],[2]), Forsberg ([3],[4]), Das and Tyagi[5], Marklund[6], and Seifbarghy and Jokar[7] have considered all the stages of a supply chain as a single firm, i.e., all the sites belong to the same organization. They have studied centralized models in the inventory system of two-level supply chains with respect to the type of demand distribution function, the type of shortage (lost-sale or backorder) and the inventory replenishment policy. These models include a central warehouse and a number of retailers. The retailers face stochastic demand. They have developed an exact or an approximate method to evaluate the total system cost. The total system cost consists of the holding cost at the warehouse and at the retailers as well as the shortage cost at the retailers. Silver et al.[8] investigated a supply chain consisting of one warehouse and one retailer in which the external demand rate was known with certainty.

Parlar and Wang[9] modelled the system ofsingle-supplier and a group of homogeneous customers with linear demand function. They incorporated quantity discounts into lot-sizing and pricing decisions and showed that quantity discount schedule could be very efficient in obtaining the maximum gain the seller and the buyer can possibly obtain together.

Goyal[10] first introduced the idea of a joint total of a joint total cost for a single-vendor and a single buyer scenario, under the assumption of having an infinite production rate for the vendor and a lot for lot policy for the shipments from the vendor to the buyer. Banerjee[11] relaxed this infinite production rate assumption of[10]. Goyal[12] then contributed to the efforts of generalizing the problem by relaxing the assumption of lot for lot. He assumed that the production lot is shipped in an integer multiple of buyer’s order size. Later, Goyal[13] provided a model where the shipment size was increased by a factor equal to the ratio of production rate to demand rate. He formulated the problem and developed an optimal expression for the first shipment size as a function of the number of shipments.

Hill[14] generalized the model of[13] by taking the geometric growth factor as a decision variable. He suggested a solution method based on an exhaustive search for both the growth factor and the number of shipments in certain ranges. Later, Hill[15] relaxed the assumptions of the shipment policy and developed an optimal solution of the problem. He showed that the structure of the optimal policy included shipments increasing in size, according to a geometric series, followed by equal-sized shipments.

Abdul–Jalbar et al.[16] have compared the effect of centralization versus decentralization on the total cost. They have considered a two level supply chain consisting of one warehouse and a number of retailers. By numerical examples they have showed that as the number of retailers increases so does the number of instances in which the decentralized policy is better. However, given a number of retailers, sensitivity analysis has indicated that under specific conditions of the replenishment and holding cost at the warehouse the centralized policy is better.

Chen and Chen[17] have presented a joint replenishment arrangement with a two echelon supply chain having one supplier or manufacturer and one buyer or retailer, facing a deterministic demand and selling a number of products in the marketplace. They have considered a situation involving a major set up cost and minor processing cost. The retailer also has major set up costs due to economies of scale in transportation and distribution expenses and an item specific minor setup cost for each additional item involved in the order. They have proposed both centralized and decentralized decision models to determine the best solution to minimize costs and by a search algorithm they have numerically illustrated the benefits generated from such an arrangement.

Andersson and Marklund[18] have studied decentralized inventory control in a two level distribution system. A two level distribution system with a central warehouse and N non-identical retailers have been considered in their work. All installations have used continuous review installation stock (R, Q) policies. They have presented an approximate cost evaluation technique where the retailers replace their stochastic lead times by correct averages. They have introduced a modified cost structure at the warehouse to decompose the multi-level inventory control problem into (N+1) single level sub problems, one problem per installation. Li and Liu[19] have considered a supplier-buyer system with probabilistic customer demand. They have showed that quantity discount policy is a way to achieve coordination. They have proposed a method to divide the profit due to joint decision between the buyer and supplier and the optimal quantity discount policy is obtained by using this profit sharing method.

Baboli et al.[20] have considered a two-level supply chain consisting of one warehouse and one retailer. In their model they have determined the optimal ordering policy on the basis of inventory and transportation costs. The demand rate by the retailer has been assumed to be known and shortages have been allowed neither at the retailer nor at the warehouse. They have studied this model in two cases: decentralized and centralized. They have proposed an algorithm to find economic order quantities of individual items for both the retailer and the warehouse which have minimized the total system cost in the centralized case compared to decentralized case and in this case they have also used the saving sharing mechanism through quantity discount to motivate the retailer to accept centralized decisions. Whereas Thangam and Uthayakumar[21] have considered a single-item, two-level, continuous review inventory model for a number of identical retailers and a single supplier system with stochastic lead time for retailer’s orders and derived a total cost function to find optimal reorder points for given batch sizes in all installations.

Zhang et al.[22] have studied a two-stage multi-item inventory system consisting of material warehouses and factories where factories have stochastic demands. They have developed stochastic optimization models of the system and provided a hybrid genetic algorithm (HGA) to minimize the long-run average system costs comprising setup cost, inventory cost. However, the joint replenished policy is analysed in this paper taking into account inventory and transportation costs for a single-warehouse single-retailer supply chain in both cases of the two stages operating individually and operating as a single organization.

3. Model Formulation

Different costs concerning with warehouse and retailer are holding cost, ordering cost, transportation cost, labor cost.

3.1. Assumptions

● Demand rate is constant for the retailer.

● Ordering cost is fixed for a certain amount

● Transportation cost is considered from warehouse to retailer and the warehouse incurs this cost.

● Shortage is allowed neither at the warehouse nor at the retailer.

● The lead time for an order to arrive at the retailer from warehouse is constant.

● The lead time for the warehouse constant.

● There is no lot-splitting at the warehouse.

● Order quantity doesn’t exceed the capacity of vehicle.

● EOQ is determined for multi-items individually.

3.2. Notations

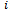●: Index of an item,

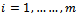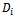●: Demand rate of the retailer for item

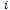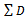●: Total demand rate of the retailer for all the items in total.

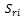●: Ordering cost of the retailer for item

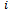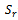●: Total ordering cost of the retailer.

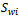●: Ordering cost of the warehouse for item

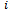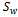●: Total ordering cost of the warehouse.

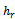●: Holding cost rate at the retailer

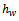●: Holding cost rate at the warehouse

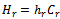●: holding cost at the retailer.

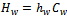●: holding cost at the warehouse.

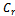●: Unit cost of items for retailer.

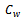●: Unit cost of items for retailer.

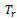●: Order cycle time of the retailer

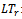●: Lead time for the retailer

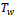●: Order cycle time of the warehouse

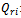●: Order quantity of the retailer for item

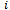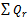●: Total order quantity of the retailer.

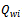●: Order quantity of the warehouse for item

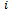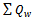●: Total order quantity of the warehouse.

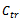●: Transportation cost from warehouse to retailer.

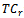●: Total cost of the retailer

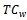●: Total cost of the warehouse

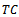●: Total system cost

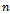● : Integer multiple of order quantity.

3.3. Cycle View of a Supply Chain

The processes in a supply chain are divided into a series of cycles as shown in Figure 1, each performed at the interface between two successive stages of a supply chain. In this study, only two stages of supply chain are considered and the corresponding cycle is replenishment cycle.

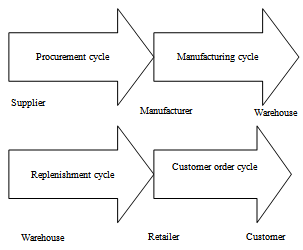Figure 1. Cycle view of a supply chain

3.4. Decentralized Case

In the decentralized case, the retailer and the warehouse intend to optimize their own costs independently. Demand rate at the retailer and transportation time to the retailer is supposed to be constant. Shortage is not allowed at the retailer therefore the retailer has a simple EOQ model and inventory level as shown in Figure 2.

The total cost of retailer is the sum of holding and ordering costs. The total cost and economic order quantity of retailer are respectively as follows:

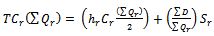(1)

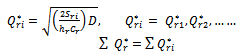(2)

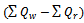Now for warehouse no shortage is allowed. We consider that the order quantity of warehouse is integer multiple of the order quantity of retailer. For warehouse the maximum level of inventory will be. Nature of inventory levels at warehouse is shown in Figure 3.

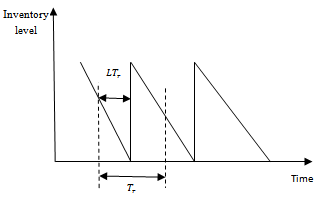Figure 2. Inventory level of retailer

In the decentralized case the total cost of warehouse is the sum of the holding and ordering costs plus the transportation cost for multi-items from warehouse to retailer. Thus the total cost of the warehouse is

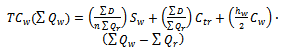(3)

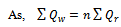(4)

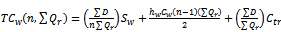(5)

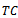Now setting the derivatives of with respect to 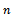equal to zero, the approximate optimal value of,

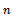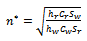(6)

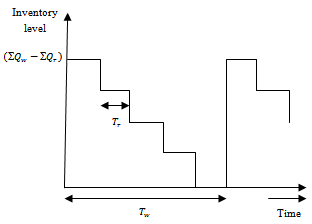Figure 3. Inventory level of warehouse

3.5. Centralized Case

In the centralized case the objective is to find the optimal cost for both the retailer and the warehouse. The total ordering cost for multi-items can be obtained by using following equation:

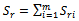(7)

The total system cost is the sum of holding and ordering cost at both the retailer and warehouse plus the transportation cost from warehouse to retailer. Thus the total system cost will be –

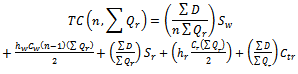(8)

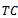If we set the derivatives of with respect to 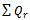and 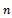equal to zero, we get

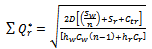(9)

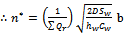(10)

We can also write n as follows:

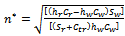(11)

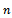From the above relation it is clear that and 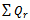is inversely related.

4. Algorithm for Centralized Case

The steps of algorithm for centralized decisions are listed below:

● Determine the total ordering cost of retailer by using equation 7.

● Set, 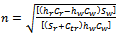for determining the value of.

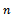● Then set, 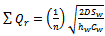for determining the value of optimum order quantity.

● Compare the total cost for centralized and decentralized decisions and find the optimum cost and economic order quantity for this cost.

5. Case Study

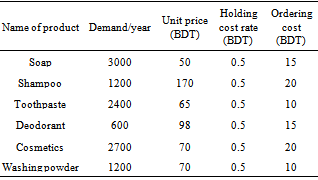
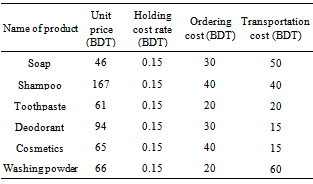
We carry out a case study implementing the developed model and the algorithm in a real situation. The study is done on six products of Unilever Bangladesh Limited considering one warehouse and one retailer. All the data are approximate values. The ordering cost for all products are collected from the company and based on this data the individual ordering cost is assumed for every product according to the volume and labor requirements. Ordering cost consists of cost per order, labor cost for loading and unloading which is obtained from equation 7. The demand of retailer per year, holding cost, ordering cost, unit cost of each product are shown in Table 1.

From warehouse of Unilever Bangladesh Limited some approximate costs are collected as shown in Table 2. Here it is found that holding cost is lower than retailer but ordering cost is twice than that of retailer. The transportation cost for these six products is 200 BDT which is then distributed over the products with respect to volume of each item.

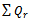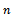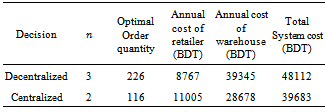
Cost analysis is done by determining the value of and n. the value of is determined from equation (6) for decentralized case and equation (11) for centralized case. For these two values we get two values of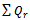. For centralized case the ordering cost for retailer reduces because per order cost include loading and unloading costs of labor but total ordering cost increases highly as a result of increase in total cost of retailer. This comparison is shown in Table 3.

Table 1. Approximate value of demands and different costs for retailer

Table 2. Approximate value of different costs for warehouse

Table 3. Cost analysis and comparison

Loss and saving in percentage for retailer and warehouse in centralized decision are summarized in Table 4.

Table 4. Loss or saving in centralized case

6. Results and Discussions

Supply chain consists of all parties who are directly or indirectly related to fulfil a customer request. It means not that all supply chain must consist of all stages. It depends on the type of product and network design of supply chain. The supply chain which is considered here only two stages are described. To find out the optimum order quantity for multi-items is the main concern. To fulfil this purpose two types of decisions are considered. One is centralized and other is decentralized. In decentralized decision, the warehouse and the retailer are concerned about only the profit of their own stage. But this is not the goal of any supply chain. To increase the total value of all stages is the goal of supply chain. This concept is used in centralized decision.

From the above numerical results the optimum order quantity and optimum cost is achieved. It is found that optimum order quantity is selected for centralized decisions. Because total supply chain profitability is obtained more in centralized decisions rather than decentralized decisions. For centralized decision the saving of warehouse is 27.12% which is more than decentralized decision and the total system saving is 1.59%. So this decision may be used by this company for practical proof.

7. Conclusions

This paper looked for the optimal ordering policy of multiple items in a two-level supply chain in two cases: centralized and decentralized. An algorithm was proposed to find out multiple item aggregated economic order quantities for both the retailer and the warehouse which minimize the total system cost in the centralized case. The case study indicated that the centralized case leads to savings for the warehouse and the whole system as compared to the decentralized case. But centralized decisions incur losses for the retailer. These losses can be covered and the retailers can be motivated if warehouse will share its saving through discount quantity.

This paper considers only two stages in a supply chain without the effect of other stages. The ordering cost of warehouse is considered twice than retailer and for centralized decision per order cost of retailer decreases for decreasing the order quantity but total ordering cost per year increases. The transportation cost is considered only from warehouse to retailer with less truck load. So there is a scope to extend this paper for multi-items, multi-suppliers condition. For multi-vehicle supply chain this paper will be one of the bases to do work.

ACKNOWLEDGEMENTS

We are particularly indebted to the company– Unilever Bangladesh Limited that provided access for this research.