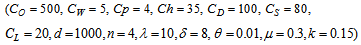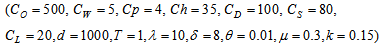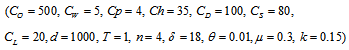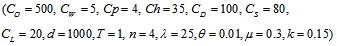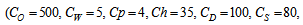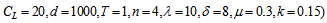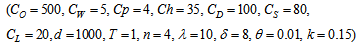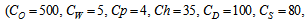-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2013; 3(2): 13-27
doi:10.5923/j.ajor.20130302.01
Partial Backlogging EOQ Model for Queued Customers with Power Demand and Quadratic Deterioration:Computational Approach
Mishra S S, Singh P K
Department of Mathematics & Statistics (Centre of Excellence on Advanced Computing) Dr.Ram Manohar Lohia Avadh University, Faizabad, 224001, UP, India
Correspondence to: Mishra S S, Department of Mathematics & Statistics (Centre of Excellence on Advanced Computing) Dr.Ram Manohar Lohia Avadh University, Faizabad, 224001, UP, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, an EOQ model for perishable items for queued customers is developed in which shortages are allowed and partially backlogged. The backlogging rate is taken to be inversely proportional to the waiting time for the next replenishment. Demand follows power pattern on time t. The model is fairly general due to dynamic nature of demand. When fresh and new items arrive in stock they begin to decay after a fixed time interval called the life period of items. The total cost function is constructed and subjected to the optimization which in turn gives us the non linear equation. Further, a computing algorithm is proposed to find the solution of the system by using the N-R method. We compute the optimal inventory period and total optimal average cost as most important performance measures for the model. Finally, numerical examples are provided to illustrate the problem and sensitivity analysis has been carried out.
Keywords: Computational Approach, Power Demand, Queued Customer, Partial Backlogging, Deterioration
Cite this paper: Mishra S S, Singh P K, Partial Backlogging EOQ Model for Queued Customers with Power Demand and Quadratic Deterioration:Computational Approach, American Journal of Operational Research, Vol. 3 No. 2, 2013, pp. 13-27. doi: 10.5923/j.ajor.20130302.01.
Article Outline
- 2000 Mathematical Classification 90Bxx, 90 B05
1. Introduction
- Kaleidoscopic pattern of inventory control system with deterioration is much more difficult to be investigated by the researchers engaged in the field. In its investigative design and framework, mathematical ideas have exceedingly shown well for dwelling upon the concern of inventory control system with aforesaid pattern of inventory. Deterioration of inventory encompasses commodities such as such as foods, vegetable, drugs, pharmaceuticals, medicine, gasoline, blood and radioactive substances deterioration takes place during the normal storage period of the units. As a result, while determining the optimal inventory policy of that type of products, the loss due to deterioration cannot be ignored. In the literature of inventory theory, the deteriorating inventory models have been continually modified so as to accumulate more practical features of the real inventory systems. A number of authors have discussed inventory models for non deteriorating items. However, there are certain substances in which deterioration plays an important role and items cannot be stored for a long time. When the items of the commodity are kept in stock as an inventory for fulfilling the future demand, there may be the deterioration of items in the inventory system. Various types of inventory models for items deteriorating at a constant rate were discussed by[1],[2],[3] and[4] etc.In practice it can be observed that constant rate of deterioration occurs rarely. Most of the items deteriorate fast as the time passes. Therefore, it is much more realistic to consider the variable deterioration rate. In a realistic product life cycle, demand is increasing with time during the growth phase.[5] investigated an inventory system with power demand pattern for items with variable rate of deterioration. [6] studied the inventory system with two-parameter exponential distributed hazardous items in which production and demand rate were constant.[7] considered an EOQ model in which inventory is depleted not only by demand, but also by deterioration at a Weibull distributed rate, assuming the demand rate with a ramp type function of time. [8] developed an inventory model for a deteriorating item having an instantaneous supply, a quadratic time-varying demand and shortages in inventory. They had taken a two-parameter Weibull distribution to represent the time to deterioration.[9] considered an inventory model for deteriorating items in which demand increases with respect to time, deterioration rate, inventory holding cost and ordering cost are all continuous functions of time. Shortages are completely backlogged. The planning horizon is finite. [10] formulated an order-level lot-size inventory model for a time-dependent deterioration and exponentially declining demand.[11] reviewed the recent studies about the deteriorating items inventory management research status. They provided a comprehensive introduction, compared with the extant reviews and proposed some key factors which should be considered in the deteriorating inventory studies. This survey provides a clear overview of the deteriorating inventory study field, which can be used as a starting point for further study. A key assumption of the basic EOQ model is that stock outs are not permitted. Relaxing the basic EOQ that stock outs are not permitted led to the development of EOQ model for the two basic stock out cases: backorders and lost sales. What took longer to develop was a model that recognized that, while some customers are willing to wait for delivery, others are not. Either these customers will cancel their orders or the supplier will have to fill them within the normal delivery time by using more expensive supply methods. While there have been a number of models developed for the EOQ model with partial backordering, most of them incorporate considerably more complicated assumption sets than the classic EOQ model do. Furthermore, when the shortage occurs, some customers are willing to wait for back order and others would turn to buy from other sellers. [12] developed economic order quantity models that focused on deteriorating items having a deterministic demand pattern with a linear trend and shortages. They assumed that the inventory deteriorates over time at a constant rate. The inventory replenishment policy was considered over a finite time-horizon.[13] considered an inventory model for items with Weibull distributed deterioration. They assumed that the demand rate is a power function of time and allowed for shortages.[14] considered the variable lead-time EPQ model with shortages. He presented a new approach, without reference to the use of derivatives but with algebraic derivation, to solve the deterministic EOQ models with/without shortages. [15] developed an inventory model with ramp type demand, starting with shortage and three – parameter Weibull distribution deterioration.[16] developed an inventory model with linear demand rate. Shortages in the inventory are allowed and were completely backlogged. They had assumed that the production rate is finite and proportional to the demand rate.[17] developing an inventory model with time dependent Weibull demand rate where shortages are allowed and are completely backlogged. The production rate is assumed to be finite and proportional to the demand rate. [18] developed an order level inventory system for time dependent linearly deteriorating items with decreasing demand rate. They assumed that the demand rate is time dependent and developed two EOQ models for without shortage case and with shortage case.[19] considered the production inventory problem in which the deterioration is Weibull distribution, production and demand are quadratic function of time. Shortages of cycle are allowed in the inventory system. Researchers such as[20],[21] and[22] considered the constant partial backlogging rates during the shortage period in their inventory models. In many cases customers are conditioned to a shipping delay and may be willing to wait for a short time in order to get their first choice. In some inventory systems, such as fashionable commodities, the length of the waiting time for the next replenishment would determine whether the backlogging will be accepted or not. Therefore, the backlogging rate should be variable and dependent on the length of the waiting time for the next replenishment. When a stock out situation occurs, only a fraction of demand occurring at a given time is backordered. And that fraction is a decreasing function of the waiting time. The approach given is revenue based and does not require specifying the backorder cost or lost sale cost which is very difficult to estimate in reality. [23] investigated optimal lot sizing for an EOQ model under conditions of perishability allowing shortage and partial backlogging. He modelled the backlogging phenomenon using a new approach in which customers are considered impatient.[24] suggested a continuous review inventory model over a finite-planning horizon with deterministic varying demand and constant deterioration rate. The model allows for shortages, which are partially backlogged at a rate which varies exponentially with time. They established an optimal replenishment policy.[25] developed the deterministic EPQ model with partial backordering when a percentage of stock outs will be backordered.Many researchers have modified inventory policies for deteriorating items by considering the time proportional partial backlogging rate such as[26],[27],[28],[29],[30],[31], [32] and so on.[33] extended model of[13] by proposing a general class time-proportional backlogging rate to make the theory more complete and provided the necessary condition to find the optimal solution.[34] proposed an EOQ inventory mathematical model for deteriorating items with exponentially decreasing demand. In the model, the shortages are allowed and partially backordered. They show that the minimized objective cost function is jointly convex and derive the optimal solution. [35] described an EOQ model with time-varying deterioration, partial backlogging which depends on the length of the waiting time for the next replenishment, linearly time-varying demand function over a finite time horizon and variable replenishment cycle.[36] developed a deterministic inventory model for infinite time-horizon incorporating partial backlogging and decrease in demand. Demand at any instant depends linearly on the on-hand inventory level at that instant. Deterioration of items begins after a certain time from the instant of their arrival in stock.[37] studied a deterministic inventory model for deteriorating items under time-dependent partial backlogging and proved that the optimal replenishment solution not only exists but is also unique. [38] considered an EOQ model for deteriorating items with exponential time varying demand. They assumed that the backlogging rate is dependent on the length of the waiting time for the next replenishment.[39] presented an optimization framework to derive optimal replenishment policy for perishable items with stock dependent demand rate. The demand rate is assumed to be a function of current level inventory and the inventory deteriorates per unit time with variable deterioration rate. The shortages are allowed and partially backlogged with a variable rate, which depends on the duration of waiting time up to arrival of next lot.[40] developed a single item perishable inventory model assuming that the demand is time dependent accelerated growth-effect of accelerated growth-steady type. The deterioration of inventory starts after a certain time. Shortages are allowed and are partially backlogged. [41] considered a deterministic inventory model in which items are subject to constant deterioration and shortages are allowed. The unsatisfied demand is backlogged which is a function of time.[42] considered an order level inventory model for seasonable/fashionable products subject to ramp type demand rate. The unsatisfied demand is partially backlogged with a time dependent backlogging rate. In addition, the product deteriorates with a time dependent deterioration rate.[43] developed a deterministic inventory model for deteriorating items in which shortages are allowed and partially backlogged. Recently, authors[44],[45] and[46] have attempted computational approach to various inventory models and discussed their applications. [47] developed a partial backlogging inventory model. They proposed the prediction method and algorithms for ordering period as well as for minimum total cost.[48] presented Economic Production Lot Size model with constant deterioration. Shortages are permitted in inventory with partial backlogging.[49] described an EOQ model for a deteriorating item considering general time-dependent demand, time-dependent partial backlogging over a finite time horizon and variable replenishment cycle.[50] developed an inventory model with time dependent two-parameter Weibull demand rate whose deterioration rate increases with time. Each cycle has shortages, which have been partially backlogged.There are a number of situations in which a customers or vendors of some sort are assumed to receive the demand in bulk of inventory are subject to put in queue at a service facility. The goal of queuing is essentially to trade-off the cost of providing a level of service capacity and the customers waiting for service.With this motivation, in the present paper an attempt is made to formulate a partial backlogging inventory model by incorporating the deterioration effect and time-dependent power pattern demand rate. Deterioration of items begins after a certain time from the instant of their arrival in stock, we name it as life time of items, and deterioration rate is a quadratic function of time. Unsatisfied demand is partially backlogged with a variable rate. To suit present day competition in the market, the backlogging rate is inversely proportional to the duration of waiting time up to arrival of next lot. The differential equations are derived and the instantaneous state of inventory is obtained analytically. The total cost function, which consists of setup cost, holding cost, backordering cost, lost sale cost, deterioration cost, waiting cost and procurement cost is constructed and subjected to the optimization which in turn gives us the system of non linear equations. Further, a computing algorithm is proposed to find the solution of the system by using the N-R method. We compute the optimal inventory period and total optimal average cost as most important performance measures for the model. Numerical demonstration and sensitivity analysis have been carried out for the model to identify the most sensibilities of various parameters involved in the system leading to interesting observations which seem to be consistent with its economic insights. This model is much useful for analysing the planning of the seasonal and fashionable products with the notion of decay or obsolete.
2. Assumptions and Notations
- In this paper we have made the following notations and assumptions in the formulation of proposed mathematical model of the inventory system.
2.1. Notations
- I (t) : the inventory level at any time t, t ≥ 0.S : the initial inventory level.μ : the life time of items.
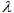 : the average arrival rate.
: the average arrival rate. : the average service rate.LS : the number of customers waiting for inventory.CO : the set up cost for each replenishment.CH : inventory holding cost per unit time.CD : deterioration cost per unit.CS : shortage cost for backlogged items.CL : the unit cost of lost sales.CW : waiting cost per customer per unit time.CP : procurement cost.T : the planning horizon.TAC (t1) : the total average cost.
: the average service rate.LS : the number of customers waiting for inventory.CO : the set up cost for each replenishment.CH : inventory holding cost per unit time.CD : deterioration cost per unit.CS : shortage cost for backlogged items.CL : the unit cost of lost sales.CW : waiting cost per customer per unit time.CP : procurement cost.T : the planning horizon.TAC (t1) : the total average cost.2.2. Assumptions
- I. A single item is considered over the fixed period T units of time. II. Customers are waiting in line for getting inventory items. They arrive on a precise schedule (deterministic) of evenly spaced intervals and service process is well scheduled.III.
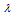 and
and 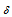 are assumed to be constant and are related by
are assumed to be constant and are related by 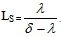 IV. Deterioration of the items takes place after the life time of items.V. The variable deterioration rate θ(t) is time dependent quadratic function such that θ(t) = θt2, 0<θ<<1.
IV. Deterioration of the items takes place after the life time of items.V. The variable deterioration rate θ(t) is time dependent quadratic function such that θ(t) = θt2, 0<θ<<1.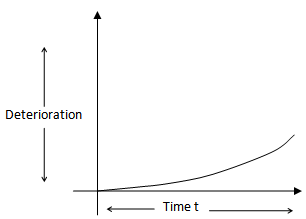 | Figure 1. Deterioration-time relationship |
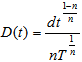 , where d is the fixed quantity, n is the parameter of power demand pattern, the value of n may be any positive number. X. Shortages are allowed and backlogging rate is
, where d is the fixed quantity, n is the parameter of power demand pattern, the value of n may be any positive number. X. Shortages are allowed and backlogging rate is 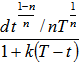 , when inventory is in shortage. The backlogging parameter k is positive constant and 0
, when inventory is in shortage. The backlogging parameter k is positive constant and 03. Mathematical Model
3.1. Model Formulation and Solution
- Let us assume that Q be the total amount of inventory produced or purchased at the beginning of each cycle. After fulfilling the backorders let we get an amount S (>0) as initial inventory. During the period (0, μ) the inventory level gradually decreases due to market demand only. After life time deterioration can take place, therefore during the period (μ, t1) the inventory level gradually abates due to market demand and deterioration of items and falls to zero at time t1. Shortages take place in the periods (t1, T) which are partially backlogged. The depletion of inventory level is shown in the following figure.The differential equations governing the inventory level
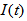 at any time t during the cycle (0, T ) are given as following,
at any time t during the cycle (0, T ) are given as following,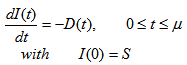 | (3.1) |
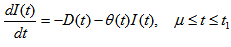 | (3.2) |
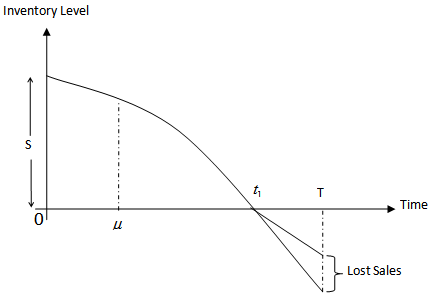 | Figure 2. Partial Backlogging Inventory Model |
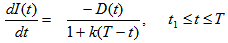 | (3.3) |
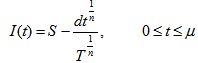 | (3.4) |
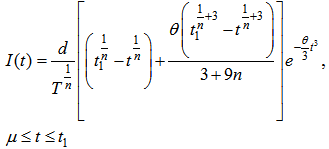 | (3.5) |
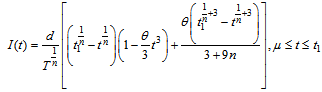 | (3.6) |
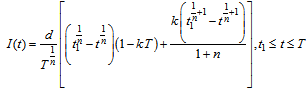 | (3.7) |
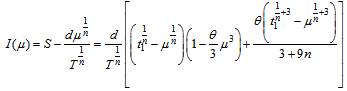 So that, the value of initial inventory level (S) is given by
So that, the value of initial inventory level (S) is given by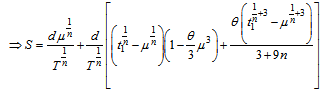 | (3.8) |
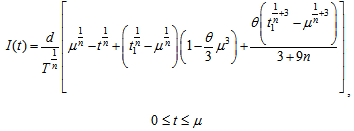
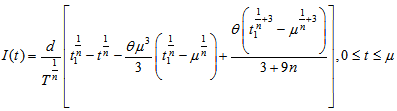 | (3.9) |
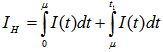 Using equation (3.9) and equation (3.6) we get
Using equation (3.9) and equation (3.6) we get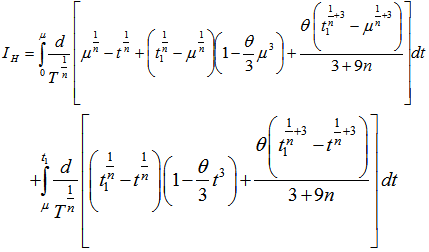 Calculating further we get
Calculating further we get 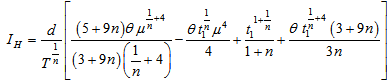 | (3.10) |
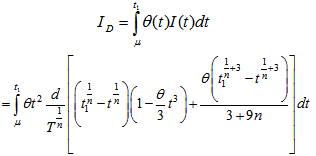 Integrating this, neglecting the term containing θ2 or higher degree of it as
Integrating this, neglecting the term containing θ2 or higher degree of it as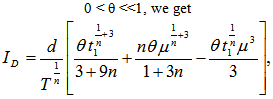 | (3.11) |
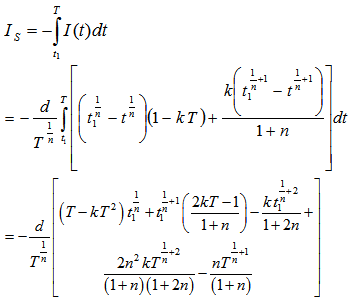 | (3.12) |
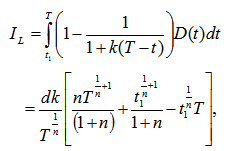 | (3.13) |
3.2. Cost Analysis and Optimization
- The total waiting cost for the customers in the system
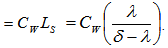 .Total average cost of the system per unit time is given by
.Total average cost of the system per unit time is given by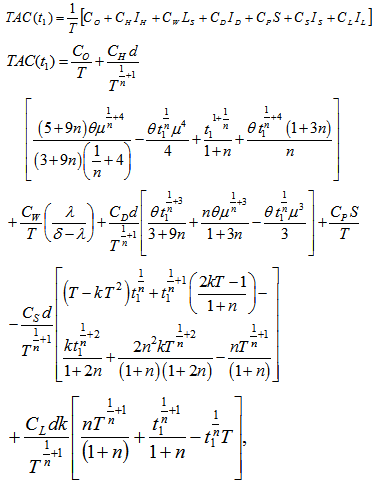 | (3.14) |
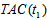 , the optimal value of t1 can be obtained by solving the following equation
, the optimal value of t1 can be obtained by solving the following equation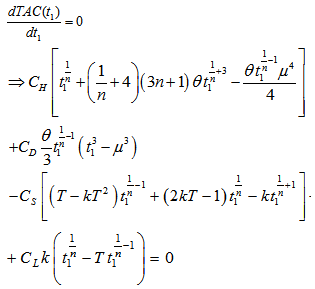 | (3.15) |
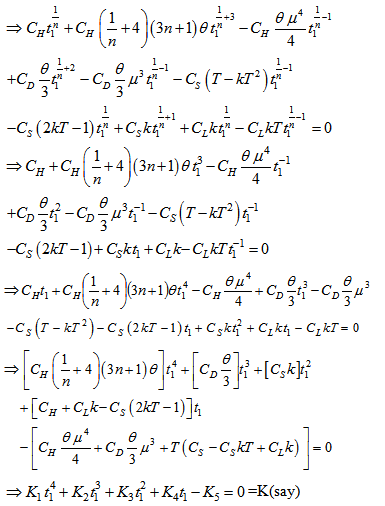 | (3.16) |
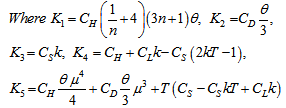 Equation (3.16) is a non-linear equation in t1 and its value is obtained by using N-R method and following algorithm by using C++ provided total cost is minimum and its second derivative is positive for being t1 optimal. The following value of second derivative in (3.17) is tested true after required parameters are computed
Equation (3.16) is a non-linear equation in t1 and its value is obtained by using N-R method and following algorithm by using C++ provided total cost is minimum and its second derivative is positive for being t1 optimal. The following value of second derivative in (3.17) is tested true after required parameters are computed 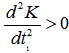 | (3.17) |
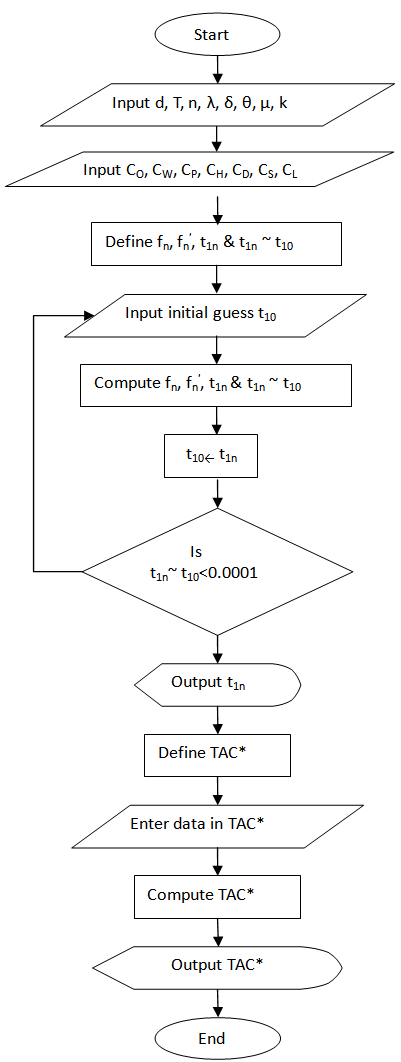 | Figure 3. Computing Algorithm |
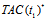 are computed finally as optimal.
are computed finally as optimal.3.3. Computing Algorithm
- Following computing algorithm is developed to find out the optimal inventory period and total optimal average cost of the inventory system.
4. Sensitivity Analysis
4.1. Numerical Example
- We have considered the following parameter values to illustrate the model numerically.
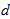 =1000 units,
=1000 units, 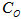 =Rs. 500 per order,
=Rs. 500 per order, 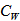 =5,
=5, 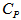 =4,
=4, 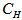 =Rs. 35 per unit per year,
=Rs. 35 per unit per year, 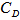 =100 per unit,
=100 per unit, 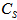 =Rs. 80 per unit per year,
=Rs. 80 per unit per year, 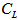 =Rs. 20 per unit,
=Rs. 20 per unit, 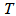 =1 year,
=1 year, 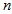 =4 units,
=4 units, 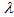 =10,
=10, 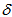 =8,
=8, 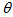 =0.01 unit,
=0.01 unit, 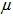 =0.3 year,
=0.3 year, 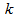 =0.15 unit. Then to minimize the total average cost, optimal values of the decision variables are obtained as
=0.15 unit. Then to minimize the total average cost, optimal values of the decision variables are obtained as 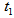 =0.766271 year,
=0.766271 year, 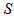 =1000.108444 units,
=1000.108444 units, 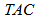 =Rs. 6933.95 per year.
=Rs. 6933.95 per year. 4.2. Tables, Graphics and Observations
- The aim of the sensitivity analysis is to demonstrate the variability of the model based on the simulations or the hypothetical data-input. In this chapter, we prefer the hypothetical data-input to run the search program of the system. It is the process of varying model parameters over a reasonable range and observing the relative changes in the model response. Remarkable are the observed changes in the optimal cycle time and total optimal average cost of the system.We wrote a program in C++ to apply a one-variable version of N-R method to compute the optimal cycle time and consequently the total optimal average cost of the system is also computed. In sensitivity analysis, variational effect of parameters on the total optimal average cost is presented.
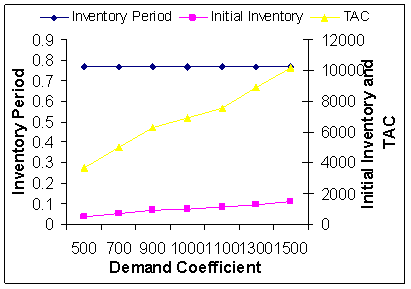 | Figure 4. Demand Coefficient d Vs. Optimal Total Average Cost |
|
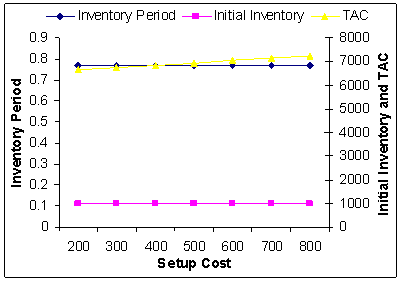 | Figure 5. Setup Cost 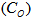 Vs. Optimal Total Average Cost (TAC*) Vs. Optimal Total Average Cost (TAC*) |
|
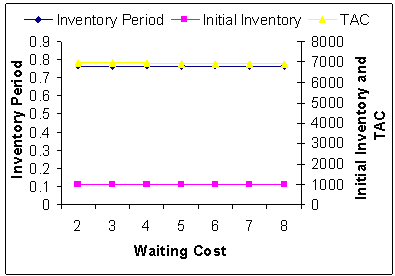 | Figure 6. Waiting Cost 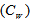 Vs. Optimal Total Average Cost (TAC*) Vs. Optimal Total Average Cost (TAC*) |
|
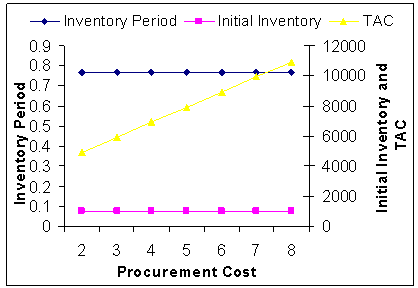 | Figure 7. Procurement Cost (Cp) Vs. Optimal Total Average Cost (TAC*) |
|
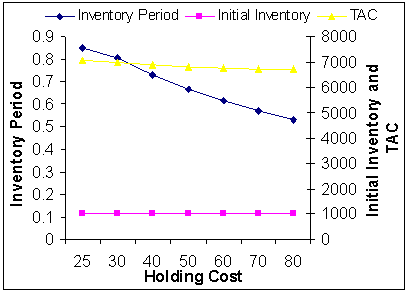 | Figure 8. Holding Cost 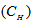 Vs. Optimal Total Average Cost (TAC*) Vs. Optimal Total Average Cost (TAC*) |
|
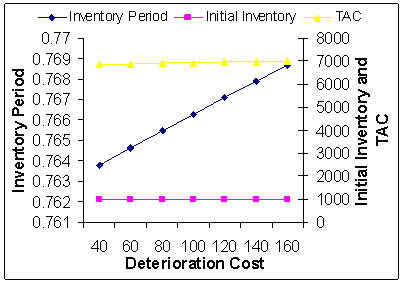 | Figure 9. Deterioration Cost (CD) Vs. Optimal Total Average Cost (TAC*) |
|
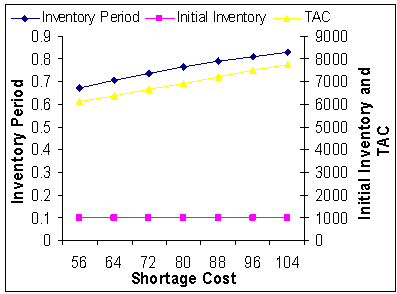 | Figure 10. Shortage Cost (Cs) Vs. Optimal Total Average Cost (TAC*) |
|
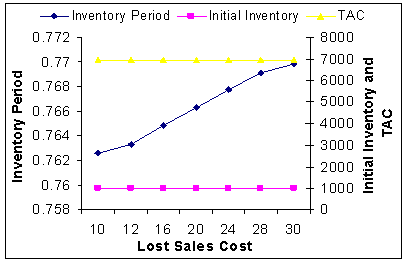 | Figure 11. Lost Sales Cost (CL) Vs. Optimal Total Average Cost (TAC*) |
|
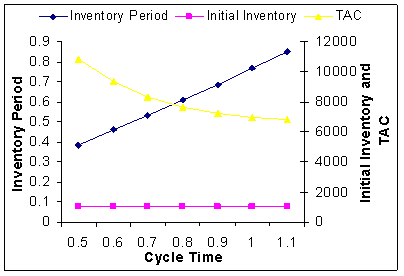 | Figure 12. Cycle Time 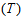 Vs. Optimal Total Average Cost (TAC*) Vs. Optimal Total Average Cost (TAC*) |
|
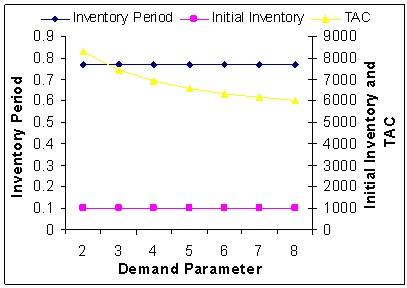 | Figure 13. Demand Parameter (n) Vs. Optimal Total Average Cost (TAC*) |
|
 | Figure 14. Average Arrival Rate(λ) Vs. Optimal Total Average Cost (TAC*) |
|
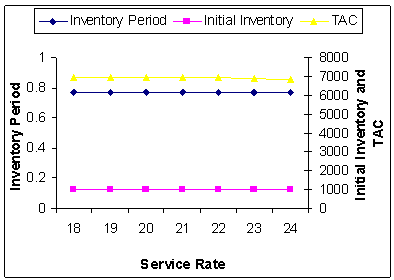 | Figure 15. Average Service Rate (δ) Vs. Optimal Total Average Cost (TAC*) |
|
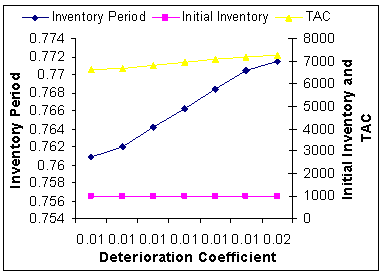 | Figure 16. Deterioration Coefficient (θ)Vs. Optimal Total Average Cost (TAC*) |
|
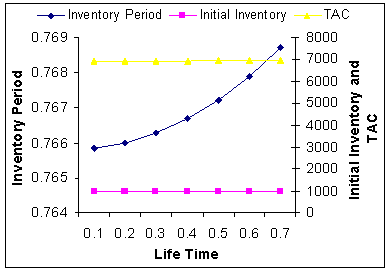 | Figure 17. Life Time (μ) Vs. Optimal Total Average Cost (TAC*) |
|
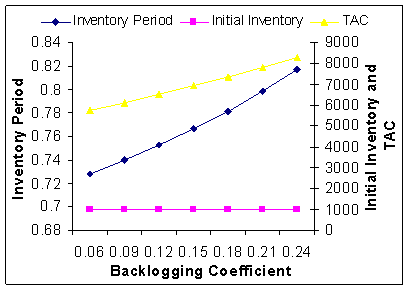 | Figure 18. Backlogging Coefficient (k)Vs. Optimal Total Average Cost (TAC*) |
5. Conclusions
- In the present paper, we have developed an inventory model for perishable items with power form time dependent demand and quadratic deterioration rate. This type of demand if occurs, then managers develop a different policy other than the conventional policy based on general ramp pattern. In cases where large portion of demand occurs at the beginning of the period we use n > 1 and if it occurs at the end of the period, we use 0 < n < 1. Constant demand rate corresponds to n = 1 and n = ∞ corresponds to instantaneous demand. Shortages are allowed and the backlogging rate is dependent on the duration of waiting time for the next replenishment and varies inversely. Shortages are partially backlogged in this model. Behaviours of different parameters have been discussed through the numerical example and sensitivity analysis. A future study will incorporate more realistic assumptions in the proposed model such as stochastic nature of demand and deterioration.
ACKNOWLEDGEMENTS
- The authors are highly thankful to the referees and editors for improving the paper in the present form and NBHM Grant 2/48(6) 2012/NBHM/R&DII/13614.
References
| [1] | Chowdhury, M.R. and Chaudhuri, K.S. (1983). An order level inventory model for deteriorating items with finite rate of replenishment. Opsearch, 20: 99-106. |
| [2] | Padmanabhan, G. and Vrat, P. (1995). EOQ models for perishable items under stock dependent selling rate. European Journal of Operational Research, 86: 281-292. |
| [3] | Balkhi, Z.T. and Benkherouf, L. (1996). A production lot size inventory model for deteriorating items and arbitrary production and demand rate. European Journal of Operational Research, 92: 302-309. |
| [4] | Yang, H.L. (2005). A comparison among various partial backlogging inventory lot-size models for deteriorating items on the basis of maximum profit. International Journal of Production Economics, 96: 119-128. |
| [5] | Dutta, T.K. and Pal, A.K. (1988). Order level inventory system with power demand pattern for items with variable rate of deterioration. Indian Journal of Pure and Applied Mathematics, 19(11): 1043-1053. |
| [6] | Baten, A. and Kamil, A.A. (2009). Inventory management systems with hazardous items of two-parameter exponential distribution. Journal of Social Sciences 5(3): 183-187. |
| [7] | Wu, J.W., Lin, C., Tan, B. and Lee, W.C. (1999). An EOQ inventory model with ramp type demand rate for items with weibull deterioration. Information and Management Sciences 10(3): 41-51. |
| [8] | Ghosh, S.K. and Chaudhuri, K.S. (2004). An order-level inventory model for a deteriorating item with weibull distribution deterioration, time-quadratic demand and shortages. Advanced Modeling and Optimization 6(1): 21-35. |
| [9] | Mehta, N.J. and Shah, N.H. (2005). Time varying increasing demand inventory model for deteriorating items. Revista Investigación Operacional 26(1): 3-9. |
| [10] | Shah, N.H. and Acharya, A.S. (2008). A time dependent deteriorating order level inventory model for exponentially declining demand. Applied Mathematical Sciences 2(56): 2795 – 2802. |
| [11] | Li, R., Lan, H. and Mawhinney, J.R. (2010). A review on deteriorating inventory study. Journal on Service Science and Management 3: 117-129. |
| [12] | Goswami, A. and Chaudhuri, K.S. (1991). An EOQ model for deteriorating items with shortages and a linear trend in demand. Journal of the Operational Research Society 42: 1105-1110. |
| [13] | Lee, W.C. and Wu, J.W. (2002). An EOQ model for items with weibull distributed deterioration, shortages and power demand pattern. Information and Management Sciences 13(2): 19-34. |
| [14] | Chang, H.C. (2004). A note on the EPQ model with shortages and variable lead time. Information and Management Sciences, 15(1): 61-67. |
| [15] | Jain, S. and Kumar, M. (2010). An EOQ inventory model for items with ramp type demand, three-parameter weibull distribution deterioration and starting with shortage. Yugoslav Journal of Operations Research 20(2): 249-259. |
| [16] | Sahoo, C.K. and Sahoo, S.K. (2010). An inventory model with linear demand rate, finite rate of production with shortages and complete backlogging. Proceedings of the International Conference on Industrial Engineering and Operations Management Dhaka, Bangladesh, January 9 – 10. |
| [17] | Tripathy, C.K. and Mishra, U. (2010). An inventory model for weibull time-dependence demand rate with completely backlogged shortages. International Mathematical Forum 5(54): 2675 – 2687. |
| [18] | Tripathy, C.K., Mishra, U. and Pradhan, L.M. (2010). An EOQ Model for Time Dependent Linearly Deteriorating Items with Shortages. International Journal of Computational and Applied Mathematics 5(2): 163–175. |
| [19] | Kalam, A., Samal, D., Sahu, S.K. and Mishra, M. (2010). A production lot-size inventory model for weibull deteriorating item with quadratic demand, quadratic production and shortages. International Journal of Computer Science and Communication 1(1): 259-262. |
| [20] | Park, K.S. (1982). Inventory models with partial backorders. International Journal of Systems Science, 13: 1313-1317. |
| [21] | Hollier, R.H. and Mak, K.L. (1983). Inventory replenishment policies for deteriorating items in a declining market. International Journal of Production Economics, 21: 813-826. |
| [22] | Wee, H.M. (1995). Joint pricing and replenishment policy for deteriorating inventory with declining market. International Journal of Production Economics, 40(2-3): 163-171. |
| [23] | Abad, P.L. (1996). Optimal pricing and lot sizing under conditions of perishability and partial backlogging. Management Science, 42(8): 1093-1104. |
| [24] | Papachristos, S. and Skouri, K. (2000). An optimal replenishment policy for deteriorating items with time-varying demand and partial exponential type backlogging. Operations Research Letters 27: 175-184. |
| [25] | Pentico, D.W., Drake, M.J. and Toews, C. (2009). The deterministic EPQ with partial backordering: a new approach. Omega 37: 624 – 636. |
| [26] | Wang, S.P. (2002). An inventory replenishment policy for deteriorating items with shortages and partial backlogging. Computers and Operational Research, 29: 2043-2051. |
| [27] | Teng, J.T. and Yang, H.L. (2004). Deterministic economic order quantity models with partial backlogging when demand and cost are fluctuating with time. Journal of the Operational Research Society, 55(5): 495-503. |
| [28] | Wu, K.S., Ouyang, L.Y. and Yang, C.T. (2006). An optimal replenishment policy for non-instantaneous deteriorating items with stock dependent demand and partial backlogging, International Journal of Production Economics, 101: 369-384. |
| [29] | Singh, S.R. and Singh, T.J. (2007). An EOQ inventory model with weibull distribution deterioration, ramp type demand and partial backlogging. Indian Journal of Mathematics and Mathematical Sciences, 3(2): 127-137. |
| [30] | Dye, C.Y., Ouyang, L.Y. and Hsieh, T.P. (2007). Deterministic inventory model for deteriorating items with capacity constraint and time-proportional backlogging rate, European Journal of Operational Research, 178 (3): 789-807. |
| [31] | Singh, T.J., Singh, S.R. and Singh, C. (2008). Perishable inventory model with quadratic demand, partial backlogging and permissible delay in payments, International Review of Pure and Applied Mathematics: 53-66. |
| [32] | Singh, T.J., Singh, S.R. and Dutt, R. (2009). An EOQ model for perishable items with power demand and partial backlogging. IJOQM, 15(1): 65-72. |
| [33] | Dye, C.Y. (2004). A note on an EOQ model for items with weibull distributed deterioration, shortages and power demand pattern. Information and Management Sciences 15(2): 81-84. |
| [34] | Ouyang, L.Y., Wu, K.S. and Cheng, M.C. (2005). An inventory model for deteriorating items with exponential declining demand and partial backlogging. Yugoslav Journal of Operations Research 15(2): 277-288. |
| [35] | Ghosh, S.K. and Chaudhuri, K.S. (2005). An EOQ model for a deteriorating item with trended demand, and variable backlogging with shortages in all cycles. Advanced Modeling and Optimization 7(1): 57-68. |
| [36] | Jain, S., Kumar, M. and Advani, P. (2008). An inventory model with inventory level-dependent demand rate, deterioration, partial backlogging and decrease in demand. International Journal of Operations Research 5(3): 154-159. |
| [37] | Valliathal, M. and Uthayakumar, R. (2009). An EOQ model for perishable items under stock and time-dependent selling rate with shortages. ARPN Journal of Engineering and Applied Sciences 4(8): 8-14. |
| [38] | Chang, H.J. and Dye, C.Y. (1999). An EOQ model for deteriorating items with exponential time varying demand and partial backlogging. Information and Management Sciences 10(1): 1-11. |
| [39] | Arya, R.K., Singh, S.R. and Shakya, S.K. (2009). An order level inventory model for perishable items with stock dependent demand and partial backlogging. International Journal of Computational and Applied Mathematics 4(1): 19–28. |
| [40] | Panda, S., Senapati, S and Basu, M. (2009). A single cycle perishable inventory model with time dependent quadratic ramp-type demand and partial backlogging. International Journal of Operational Research 5(1): 110-129. |
| [41] | Shah, N.H. and Shukla, K.T. (2009). Deteriorating inventory model for waiting time partial backlogging. Applied Mathematical Sciences 3(9): 421 – 428. |
| [42] | Skouri, K. and Konstantaras, I. (2009). Order level inventory models for deteriorating seasonable/fashionable products with time dependent demand and shortages. Mathematical Problems in Engineering, Article ID 679736: 1-24. |
| [43] | Mishra, V.K. and Singh, L.S. (2010). Deteriorating inventory model with time dependent demand and partial backlogging. Applied Mathematical Sciences 4(72): 3611-3619. |
| [44] | Mishra S S and Singh P K (2011). Computational approach to EOQ model with power form stock-dependent demand and cubic deterioration, American Journal of Operations Research, (1): p.p. 5-13 1DOI: 10.5923/j.ajor.20110101.02, 2011. |
| [45] | Mishra S S and Singh P K (2012). Computing of total optimal cost of an EOQ model with quadratic deterioration and occurrence of shortages, International journal of Management Science and Engineering Management, World Academic Press, ISSN 1750-9653, England, UK 7(4): 243-252. |
| [46] | Mishra S S and Singh P K (2012). Computational approach to an inventory model with ramp-type demand and linear deterioration, International Journal of Operations Research, p.p. 337-357, Vol. 15, No. 3. |
| [47] | Chen, M. and Zhuo, F. (2010). A partial backlogging inventory model with time-varying demand during shortage period. International Journal on Intelligent Systems and Applications 1: 23-29. |
| [48] | Kumar, M. Chauhan, A. and Kumar, P. (2011). Economic production lot size model with stochastic demand and shortage partial backlogging rate under imperfect quality items. International Journal of Advanced Science and Technology 31: 1-22. |
| [49] | Ghosh, S.K., Khanra, S. and Chaudhuri, K.S. (2011). An EOQ model for a deteriorating item with time-varying demand and time-dependent partial backlogging. International Journal of Mathematics in Operational Research 3(3): 264 – 279. |
| [50] | Tripathy, P.K. and Pradhan, S. (2011). An integrated partial backlogging inventory model having weibull demand and variable deterioration rate with the effect of trade credit. International Journal of Scientific and Engineering Research 2(4): 1-5. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML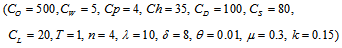
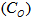 Vs. Optimal Total Average Cost (TAC*)
Vs. Optimal Total Average Cost (TAC*)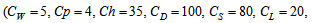
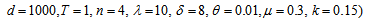
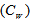 Vs. Optimal Total Average Cost (TAC*)
Vs. Optimal Total Average Cost (TAC*)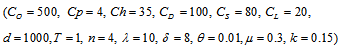

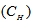 Vs. Optimal Total Average Cost (TAC*)
Vs. Optimal Total Average Cost (TAC*)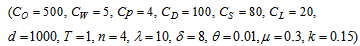
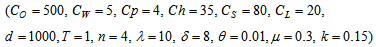
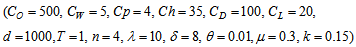
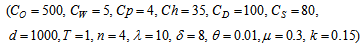
 Vs. Optimal Total Average Cost (TAC*)
Vs. Optimal Total Average Cost (TAC*)