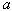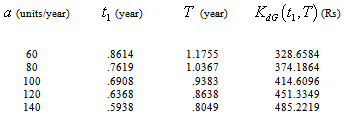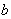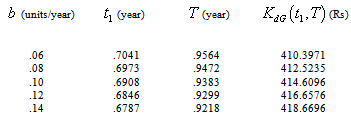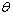-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
p-ISSN: 2324-6537 e-ISSN: 2324-6545
2012; 2(6): 81-92
doi: 10.5923/j.ajor.20120206.01
Fuzzy Inventory Model for Deteriorating Items with Time-varying Demand and Shortages
Chandra K. Jaggi1, Sarla Pareek2, Anuj Sharma1, Nidhi2
1Department of Operational Research, Faculty of Mathematical Sciences, University of Delhi, Delhi, 110007, India
2Centre for Mathematical Sciences, Banasthali University, Banasthali, 304022, Rajasthan, India
Correspondence to: Chandra K. Jaggi, Department of Operational Research, Faculty of Mathematical Sciences, University of Delhi, Delhi, 110007, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Fuzzy set theory is primarily concerned with how to quantitatively deal with imprecision and uncertainty, and offers the decision maker another tool in addition to the classical deterministic and probabilistic mathematical tools that are used in modeling real-world problems. The present study investigates a fuzzy economic order quantity model for deteriorating items in which demand increases with time. Shortages are allowed and fully backlogged. The demand, holding cost, unit cost, shortage cost and deterioration rate are taken as a triangular fuzzy numbers. Graded Mean Representation, Signed Distance and Centroid methods are used to defuzzify the total cost function and the results obtained by these methods are compared with the help of a numerical example. Sensitivity analysis is also carried out to explore the effect of changes in the values of some of the system parameters. The proposed methodology is applicable to other inventory models under uncertainty.
Keywords: Inventory, Deterioration, Shortages, Fuzzy Variable, Triangular Fuzzy Number, Graded mean representation method, Signed distance method , Centroid method
Cite this paper: Chandra K. Jaggi, Sarla Pareek, Anuj Sharma, Nidhi, "Fuzzy Inventory Model for Deteriorating Items with Time-varying Demand and Shortages", American Journal of Operational Research, Vol. 2 No. 6, 2012, pp. 81-92. doi: 10.5923/j.ajor.20120206.01.
Article Outline
1. Introduction
- In conventional inventory models, uncertainties are treated as randomness and are being handled by applying the probability theory. However, in certain situations uncertainties are due to fuzziness, and such cases are dilated in the fuzzy set theory which was demonstrated by Zadeh in[12]. Kauffmann and Gupta[1] provided an introduction to fuzzy arithmetic operation and Zimmermann[4] discussed the concept of the fuzzy set theory and its applications.Considering the fuzzy set theory in inventory modeling renders an authenticity to the model formulated since fuzziness is the closest possible approach to reality. As reality is imprecise and can only be approximated to a certain extent, same way, fuzzy theory helps one to incorporate uncertainties in the formulation of the model, thus bringing it closer to reality.Park[10] applied the fuzzy set concepts to EOQ formula by representing the inventory carrying cost with a fuzzy number and solved the economic order quantity model using fuzzy number operations based on the extension principle. Vujosevic et al.[15] used trapezoidal fuzzy number to fuzzify the order cost in the total cost of the inventory model without backorder, and got fuzzy total cost. Yao and Lee [7] introduced a backorder inventory model with fuzzy order quantity as triangular and trapezoidal fuzzy numbers and shortage cost as a crisp parameter. Gen et al.[14] expressed their input data as fuzzy numbers, and then the interval mean value concept was introduced to solve the inventory problem. Chang et al.[20] considered the backorder inventory problem with fuzzy backorder such that the backorder quantity is a triangular fuzzy number. Chang[21] discussed the fuzzy production inventory model for fuzzify the product quantity as triangular fuzzy number. Lee and Yao[5] proposed the inventory without backorder models in the fuzzy sense, where the order quantity is fuzzified as the triangular fuzzy number. Yao et al.[9] assumed to be the order quantity and the total demand rate as triangular fuzzy numbers and obtained the fuzzy inventory model without shortages. Wu and Yao[11] fuzzified the order quantity and shortage quantity into triangular fuzzy numbers in an inventory model with backorder and they obtained the membership function of the fuzzy cost and its centroid. Yao and Chiang[8] considered the total cost of inventory without backorder. They fuzzified the total demand and cost of storing one unit per day into triangular fuzzy numbers and defuzzify by the centroid and the signed distance methods. Dutta et al.[17] developed a model in presence of fuzzy random variable demand where the optimum is achieved using a graded mean integration representation. Chang et al.[3] developed the mixture inventory model involving variable lead-time with backorders and lost sales. First they fuzzify the random lead-time demand to be a fuzzy random variable and then fuzzify the total demand to be the triangular fuzzy number and derive the fuzzy total cost. By the centroid method of defuzzification, they estimate the total cost in the fuzzy sense. Wee et al.[6] developed an optimal inventory model for items with imperfect quality and shortage backordering. Lin[23] developed the inventory problem for a periodic review model with variable lead-time and fuzzified the expected demand shortage and backorder rate using signed distance method to defuzzify. Roy and Samanta[2] discussed a fuzzy continuous review inventory model without backorder for deteriorating items in which the cycle time is taken as a symmetric fuzzy number. They used the signed distance method to fuzzify the total cost. Gani and Maheswari[16] developed an EOQ model with imperfect quality items with shortages where defective rate, demand, holding cost, ordering cost and shortage cost are taken as triangular fuzzy numbers. Graded mean integration method is used for defuzzification of the total profit. Ameli et al.[13] developed a new inventory model to determine ordering policy for imperfect items with fuzzy defective percentage under fuzzy discounting and inflationary conditions. They used the signed distance method of defuzzification to estimate the value of total profit. Nezhad et al.[22] developed a periodic review model and a continuous review inventory model with fuzzy setup cost, holding cost and shortage cost. Also they considered the lead-time demand and the lead-time plus one period’s demand as random variables. They use two methods in the name of signed distance and possibility mean value to defuzzify. Uthayakumar and Valliathl[19] developed an economic production model for Weibull deteriorating items over an infinite horizon under fuzzy environment and considered some cost component as triangular fuzzy numbers and using the signed distance method to defuzzify the cost function. In this paper, an inventory model for deteriorating items with shortages is considered where demand, holding cost, unit cost, shortage cost and deterioration rate are assumed as a triangular fuzzy numbers. For defuzzification of the total cost function, Graded Mean Representation, Signed Distance and Centroid methods are used. By comparing the results obtained by these methods, we get the better one as an estimate of the total cost in the fuzzy sense.
2. Preliminaries
- In order to treat fuzzy inventory model by using graded mean representation, signed distance and centroid to defuzzify, we need the following definitions. Definition 2.1 (By Pu and Liu[18, Definition 2.1]). A fuzzy set
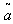 on
on  is called a fuzzy point if its membership function is
is called a fuzzy point if its membership function is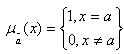 | (1) |
 .Definition 2.2 A fuzzy set
.Definition 2.2 A fuzzy set 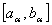 where
where  and a < b defined on
and a < b defined on 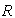 , is called a level of a fuzzy interval if its membership function is
, is called a level of a fuzzy interval if its membership function is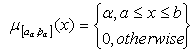 | (2) |
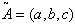 where a < b < c and defined on
where a < b < c and defined on 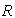 , is called a triangular fuzzy number if its membership function is
, is called a triangular fuzzy number if its membership function is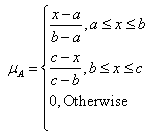 | (3) |
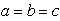 , we have fuzzy point
, we have fuzzy point 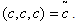 The family of all triangular fuzzy numbers on
The family of all triangular fuzzy numbers on  is denoted as
is denoted as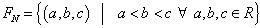 .The
.The 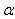 -cut of
-cut of 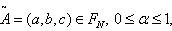 is
is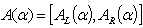 . Where
. Where 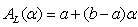 and
and 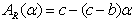 are the left and right endpoints of
are the left and right endpoints of . Definition 2.4 If
. Definition 2.4 If  is a triangular fuzzy number then the graded mean integration representation of
is a triangular fuzzy number then the graded mean integration representation of 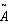 is defined as
is defined as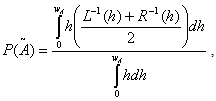 with
with 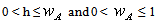 .
.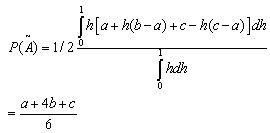 | . (4) |
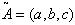 is a triangular fuzzy number then the signed distance of
is a triangular fuzzy number then the signed distance of 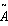 is defined as
is defined as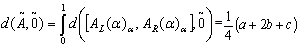 | (5) |
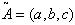 is defined as
is defined as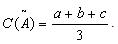 | (6) |
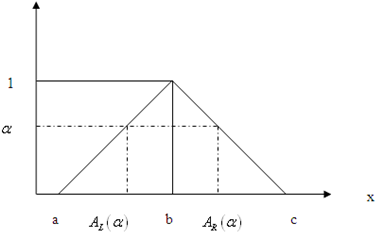 | Figure.  -cut of a triangular fuzzy number -cut of a triangular fuzzy number |
3. Assumptions and Notations
- The mathematical model in this paper is developed on the basis of the following assumptions and notations.
3.1 Notations
- (i)
 is the demand rate at any time per unit time.(ii)
is the demand rate at any time per unit time.(ii)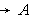 is the ordering cost per order.(iii)
is the ordering cost per order.(iii)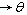 is the deterioration rate,
is the deterioration rate, 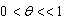 (iv)
(iv)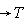 is the length of the Cycle.(v)
is the length of the Cycle.(v) 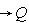 is the ordering Quantity per unit.(vi) →
is the ordering Quantity per unit.(vi) → 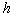 is the holding cost per unit per unit time.(vii)
is the holding cost per unit per unit time.(vii) 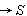 is the shortage Cost per unit time.(viii)
is the shortage Cost per unit time.(viii) 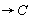 is the unit Cost per unit time.(ix) →
is the unit Cost per unit time.(ix) →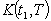 is the total inventory cost per unit time.(x)
is the total inventory cost per unit time.(x) 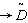 is the fuzzy demand.(xi)
is the fuzzy demand.(xi) 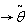 is the fuzzy deterioration rate.(xii)
is the fuzzy deterioration rate.(xii)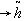 is the fuzzy holding cost per unit per unit time.(xiii)
is the fuzzy holding cost per unit per unit time.(xiii)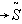 is the fuzzy shortage Cost per unit time.(xiv)
is the fuzzy shortage Cost per unit time.(xiv)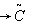 is the fuzzy unit Cost per unit time.(xv)
is the fuzzy unit Cost per unit time.(xv)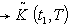 is the total fuzzy inventory cost per unit time.(xvi)
is the total fuzzy inventory cost per unit time.(xvi)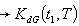 is the defuzzify value of
is the defuzzify value of 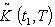 by applying Graded mean integration method(xvii)
by applying Graded mean integration method(xvii)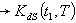 is the defuzzify value of
is the defuzzify value of 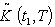 by applying Signed distance method(xviii)
by applying Signed distance method(xviii)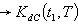 is the defuzzify value of
is the defuzzify value of 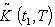 by applying Centroid method.
by applying Centroid method. 3.2 Assumptions
- (i)→Demand
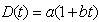 is assumed to be an increasing function of time i.e. where
is assumed to be an increasing function of time i.e. where 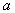 and
and 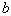 are positive constants and
are positive constants and 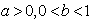 .(ii)→Replenishment is instantaneous and lead-time is zero.(iii)→Shortages are allowed and fully backlogged.
.(ii)→Replenishment is instantaneous and lead-time is zero.(iii)→Shortages are allowed and fully backlogged.4. Mathematical Model
- Let
 be the on-hand inventory at time t with initial inventory
be the on-hand inventory at time t with initial inventory 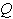 . During the period[0,
. During the period[0, 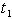 ] the on-hand inventory depletes due to demand and deterioration and exhausted at time
] the on-hand inventory depletes due to demand and deterioration and exhausted at time 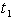 . The period[
. The period[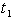 , T] is the period of shortages, which are fully backlogged. At any instant of time, the inventory level
, T] is the period of shortages, which are fully backlogged. At any instant of time, the inventory level 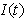 is governed by the differential equations.
is governed by the differential equations.4.1. Crisp Model
 | (4.1) |
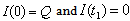 .
. | (4.2) |
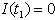 .The solution of equation (4.1) and (4.2) is given by
.The solution of equation (4.1) and (4.2) is given by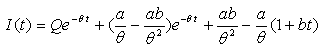 | (4.3) |
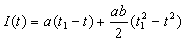 | (4.4) |
 , we have
, we have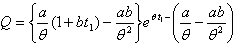 | (4.5) |
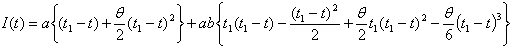 | (4.6) |
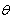 ).Total average no. of holding units (
).Total average no. of holding units (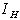 ) during period[0, T] is given by
) during period[0, T] is given by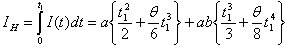 | (4.7) |
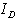 ) during period[0, T] is given by
) during period[0, T] is given by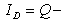 Total Demand
Total Demand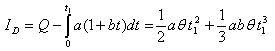 | (4.8) |
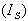 during period[0, T] is given by
during period[0, T] is given by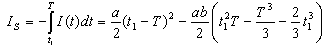 | (4.9) |
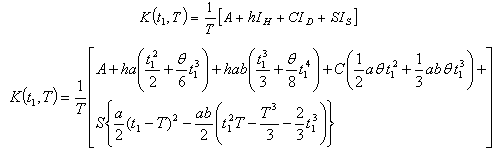 | (4.10) |
4.2. Fuzzy Model
- Due to uncertainly in the environment it is not easy to define all the parameters precisely, accordingly we assume some of these parameters namely
 may change within some limits. Let
may change within some limits. Let  are as triangular fuzzy numbers.Total cost of the system per unit time in fuzzy sense is given by
are as triangular fuzzy numbers.Total cost of the system per unit time in fuzzy sense is given by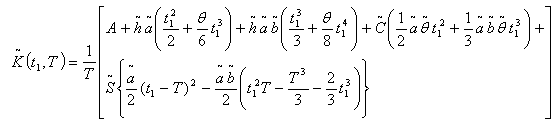 | (4.11) |
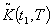 by graded mean representation, signed distance and centroid methods.(i) By Graded Mean Representation Method, Total Cost is given by
by graded mean representation, signed distance and centroid methods.(i) By Graded Mean Representation Method, Total Cost is given by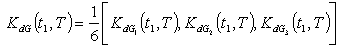 Where
Where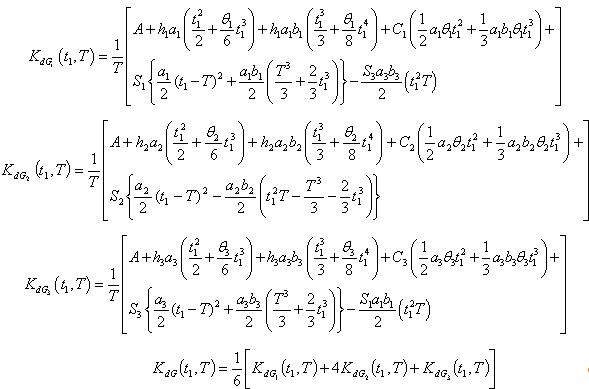 | (4.12) |
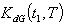 , the optimal value of
, the optimal value of 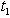 and
and 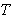 can be obtained by solving the following equations:
can be obtained by solving the following equations: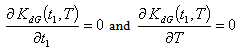 | (4.13) |
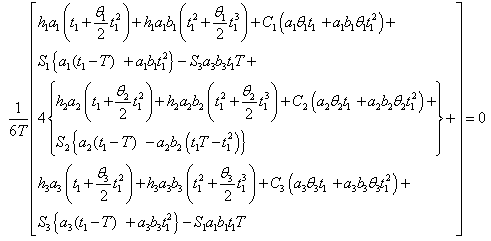 | (4.14) |
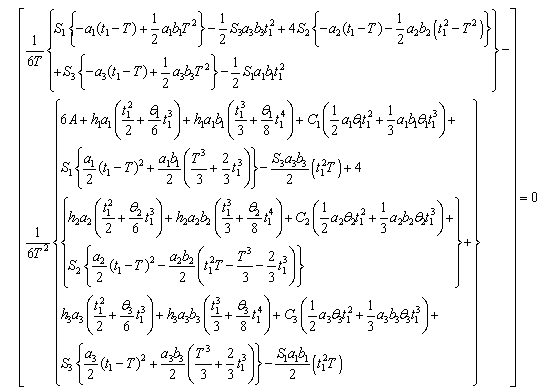 | (4.15) |
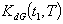 to be convex, the following conditions must be satisfied
to be convex, the following conditions must be satisfied 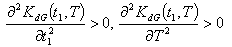 | (4.16) |
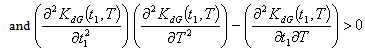 | (4.17) |
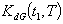 are complicated and it is very difficult to prove the convexity mathematically. Thus, the convexity of total cost function has been established graphically, (Figure (A)).(ii) By Signed Distance Method, Total cost is given by
are complicated and it is very difficult to prove the convexity mathematically. Thus, the convexity of total cost function has been established graphically, (Figure (A)).(ii) By Signed Distance Method, Total cost is given by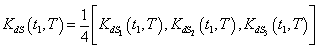 Where
Where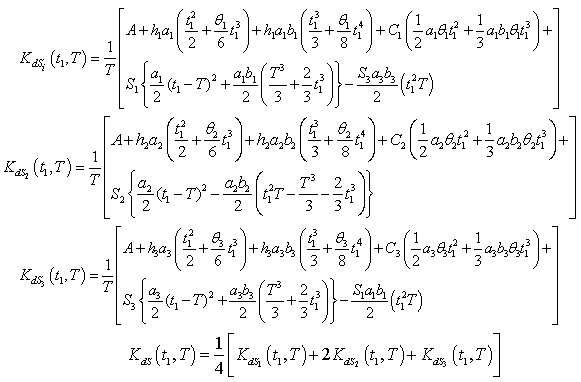 | (4.18) |
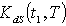 has been minimized following the same process as has been stated in case (i).To minimize total cost function per unit time
has been minimized following the same process as has been stated in case (i).To minimize total cost function per unit time 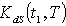 , the optimal value of
, the optimal value of 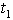 and
and 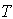 can be obtained by solving the following equations:
can be obtained by solving the following equations: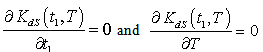 | (4.19) |
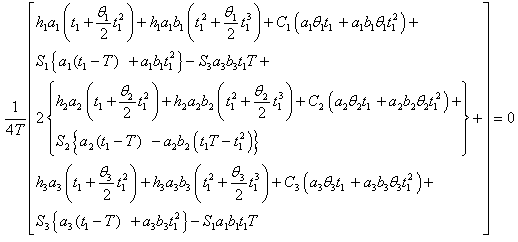 | (4.20) |
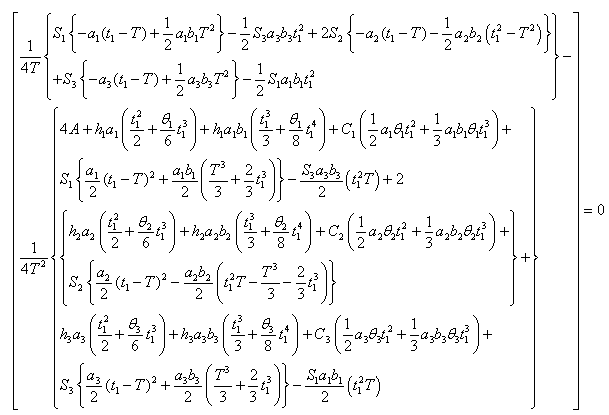 | (4.21) |
 to be convex, the following conditions must be satisfied
to be convex, the following conditions must be satisfied 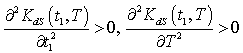 | (4.22) |
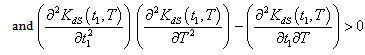 | (4.23) |
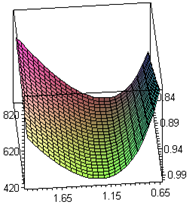
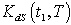 are complicated and it is very difficult to prove the convexity mathematically. Thus, the convexity of total cost function has been established graphically, (Figure (B)).(iii)By Centroid Method, Total cost is given by
are complicated and it is very difficult to prove the convexity mathematically. Thus, the convexity of total cost function has been established graphically, (Figure (B)).(iii)By Centroid Method, Total cost is given by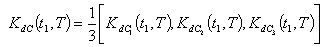 Where
Where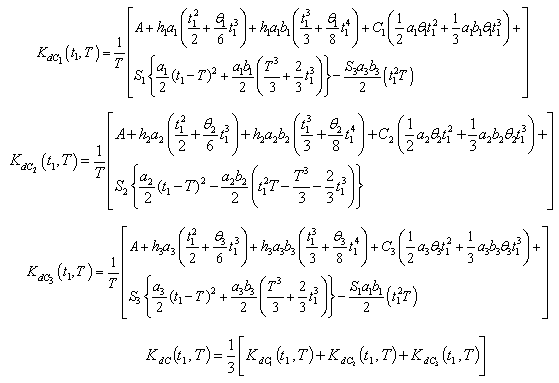 | (4.24) |
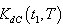 has been minimized following the same process as has been stated in case (i).To minimize total cost function per unit time
has been minimized following the same process as has been stated in case (i).To minimize total cost function per unit time 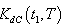 , the optimal value of
, the optimal value of 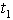 and
and 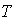 can be obtained by solving the following equations:
can be obtained by solving the following equations: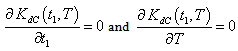 | (4.25) |
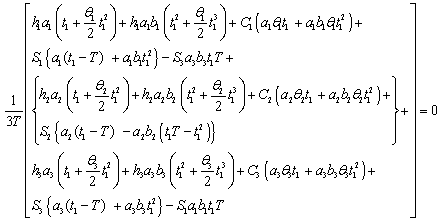 | (4.26) |
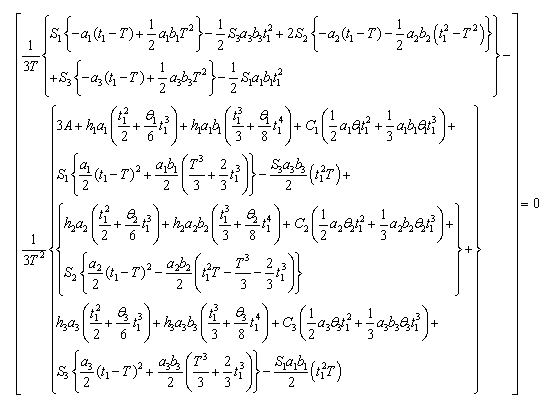 | (4.27) |
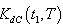 to be convex, the following conditions must be satisfied
to be convex, the following conditions must be satisfied 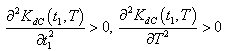 | (4.28) |
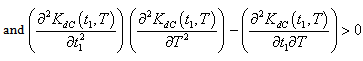 | (4.29) |
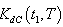 are complicated and it is very difficult to prove the convexity mathematically. Thus, the convexity of total cost function has been established graphically, (Figure (C)).
are complicated and it is very difficult to prove the convexity mathematically. Thus, the convexity of total cost function has been established graphically, (Figure (C)).5. Numerical Example
- Consider an inventory system with following parametric values.Crisp Model,
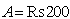 /order,
/order, 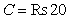 /unit,
/unit, 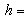 Rs. 5/unit/year,
Rs. 5/unit/year, 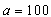 units/year,
units/year, 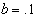 units/year,
units/year, 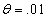 /year,
/year,  Rs 15 /unit/year.The solution of crisp model is
Rs 15 /unit/year.The solution of crisp model is 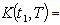 Rs 404.3429,
Rs 404.3429, 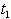 =. 7149 year, T = .9636 year.Fuzzy Model,
=. 7149 year, T = .9636 year.Fuzzy Model, 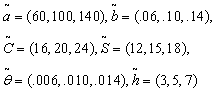 The solution of fuzzy model can be determined by following three methods. By Graded Mean Representation Method, we have1. When
The solution of fuzzy model can be determined by following three methods. By Graded Mean Representation Method, we have1. When 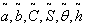 all are triangular fuzzy numbers
all are triangular fuzzy numbers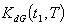 = Rs 414.6096,
= Rs 414.6096,  = .6908 year, T= .9383 year.2. When
= .6908 year, T= .9383 year.2. When 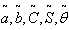 are triangular fuzzy numbers
are triangular fuzzy numbers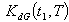 = Rs 406.9852,
= Rs 406.9852, 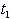 =. 7135 year, T = .9560 year.3. When
=. 7135 year, T = .9560 year.3. When 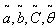 are triangular fuzzy numbers
are triangular fuzzy numbers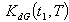 = Rs 405.5274,
= Rs 405.5274, 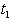 =. 7115 year, T= .9596 year.4. When
=. 7115 year, T= .9596 year.4. When 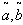 and
and 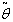 are triangular fuzzy numbers
are triangular fuzzy numbers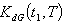 = Rs 405.2250,
= Rs 405.2250, 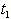 =. 7120 year, T = .9603 year.5. When
=. 7120 year, T = .9603 year.5. When 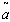 and
and 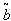 are triangular fuzzy numbers
are triangular fuzzy numbers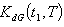 = Rs 404.8978,
= Rs 404.8978, 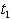 =. 7131 year, T = .9611 year.By Signed Distance Method, we have1. When
=. 7131 year, T = .9611 year.By Signed Distance Method, we have1. When 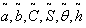 all are triangular fuzzy numbers
all are triangular fuzzy numbers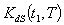 = Rs 419.6059,
= Rs 419.6059, 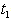 =. 6797 year, T = .9266 year.2. When
=. 6797 year, T = .9266 year.2. When 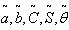 are triangular fuzzy numbers
are triangular fuzzy numbers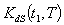 = Rs 408.2810,
= Rs 408.2810, 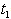 =. 7128 year, T= .9523 year.3. When
=. 7128 year, T= .9523 year.3. When 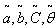 are triangular fuzzy numbers
are triangular fuzzy numbers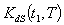 = Rs 406.1163,
= Rs 406.1163, 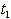 =. 7093 year, T= .9576 year.4. When
=. 7093 year, T= .9576 year.4. When 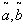 and
and 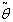 are triangular fuzzy numbers
are triangular fuzzy numbers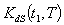 = Rs 405.6640,
= Rs 405.6640, 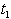 =. 7106 year, T = .9587 year.5. When
=. 7106 year, T = .9587 year.5. When 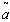 and
and 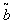 are triangular fuzzy numbers
are triangular fuzzy numbers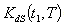 = Rs 405.1742,
= Rs 405.1742, 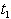 =. 7122 year, T = .9599 year.By Centroid Method, we have1. When
=. 7122 year, T = .9599 year.By Centroid Method, we have1. When 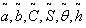 all are triangular fuzzy numbers
all are triangular fuzzy numbers 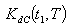 = Rs 424.5173,
= Rs 424.5173, 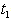 =. 6691 year, T = 9153 year.2. When
=. 6691 year, T = 9153 year.2. When 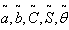 are triangular fuzzy numbers
are triangular fuzzy numbers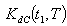 = Rs 409.5606,
= Rs 409.5606, 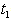 =. 7121 year, T = .9487 year.3. When
=. 7121 year, T = .9487 year.3. When 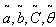 are triangular fuzzy numbers
are triangular fuzzy numbers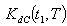 = Rs 406.7030,
= Rs 406.7030, 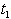 =. 7074 year, T = .9557 year.4. When
=. 7074 year, T = .9557 year.4. When 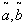 and
and 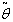 are triangular fuzzy numbers
are triangular fuzzy numbers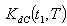 = Rs 406.1016,
= Rs 406.1016,  =. 7092 year, T = .9571 year.5. When
=. 7092 year, T = .9571 year.5. When 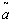 and
and 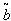 are triangular fuzzy numbers
are triangular fuzzy numbers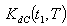 = Rs 405.4499,
= Rs 405.4499, 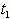 =.7113 year, T = .9587 year.
=.7113 year, T = .9587 year.6. Sensitivity Analysis
- A sensitivity analysis is performed to study the effects of changes in fuzzy parameters
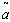 ,
, 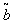 and
and 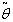 on the optimal solution by taking the defuzzify values of these parameters. The results are shown in below tables.
on the optimal solution by taking the defuzzify values of these parameters. The results are shown in below tables.
|
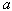 increases, fuzzy cost
increases, fuzzy cost 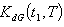 increases significantly but
increases significantly but 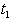 and
and 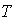 decreases drastically.
decreases drastically.
|
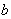 increases, fuzzy cost
increases, fuzzy cost 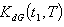 increases regularly but
increases regularly but 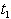 and
and 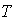 decreases gradually.
decreases gradually.
|
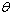 increases, fuzzy cost
increases, fuzzy cost 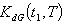 increases slightly but
increases slightly but 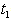 and
and 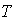 decreases gradually.If we plot the total cost function
decreases gradually.If we plot the total cost function 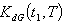 with some values of
with some values of 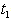 and
and 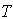 s.t.
s.t. 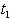 = .65 to 2 with equal interval
= .65 to 2 with equal interval 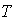 = .84 to 1, then we get strictly convex graph of total cost function
= .84 to 1, then we get strictly convex graph of total cost function 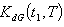 given below.
given below.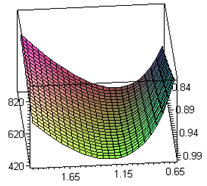 | Figure (A). Total Fuzzy Cost 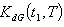 Vs. Vs. 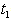 and and 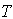 |
 | Figure (B). Total Fuzzy Cost 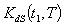 Vs. Vs. 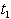 and and 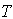 |
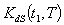 with some values of
with some values of 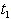 and
and 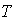 s.t.
s.t. 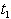 = .65 to 2 with equal interval
= .65 to 2 with equal interval 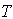 = .84 to 1, then we get strictly convex graph of total cost function
= .84 to 1, then we get strictly convex graph of total cost function 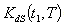 given below.If we plot the total cost function
given below.If we plot the total cost function 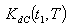 with some values of
with some values of 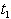 and
and 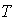 s.t.
s.t. 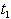 = .65 to 2 with equal interval
= .65 to 2 with equal interval 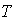 = .84 to 1, then we get strictly convex graph of total cost function
= .84 to 1, then we get strictly convex graph of total cost function 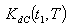 given below.
given below.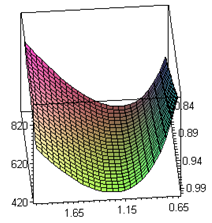 | Figure (C). Total Fuzzy Cost 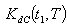 Vs. Vs. 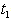 and and 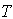 |
7. Conclusions
- This paper presents a fuzzy inventory model for deteriorating items with allowable shortages in which demand is an increasing function of time. The demand, deterioration rate, inventory holding cost, unit cost and shortage cost are represented by triangular fuzzy numbers. For defuzzification, graded mean, signed distance and centroid method are employed to evaluate the optimal time period of positive stock
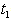 and total cycle length T which minimizes the total cost. By given numerical example it has been tested that graded mean representation method gives minimum cost as compared to signed distance method and centroid method. A sensitivity analysis is also conducted on the parameters
and total cycle length T which minimizes the total cost. By given numerical example it has been tested that graded mean representation method gives minimum cost as compared to signed distance method and centroid method. A sensitivity analysis is also conducted on the parameters 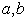 and
and 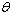 to explore the effects of fuzziness. Finding Suggest that the change in parameters
to explore the effects of fuzziness. Finding Suggest that the change in parameters 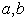 and
and 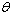 will result the change in fuzzy cost with some changes in
will result the change in fuzzy cost with some changes in 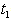 and
and 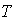 .With the increases values of these parameters will result in increase of fuzzy cost, but decreases
.With the increases values of these parameters will result in increase of fuzzy cost, but decreases 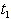 and
and 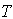 . Similarly with the decreases values of these parameters will result in decrease of fuzzy cost, but increases
. Similarly with the decreases values of these parameters will result in decrease of fuzzy cost, but increases 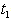 and
and 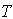 .A future study would be to extend the proposed model for finite replenishment rate, stock outs, which are partially backlogged, price dependent demand, stock dependent demand and many more.
.A future study would be to extend the proposed model for finite replenishment rate, stock outs, which are partially backlogged, price dependent demand, stock dependent demand and many more.ACKNOWLEDGEMENTS
- The authors would like to thank anonymous referees for their valuable and constructive comments and suggestions that have led to improvement on the earlier version of the paper. The first author would like to acknowledge the support of the Research Grant No.: Dean(R/R&D/2012/917), provided by the University of Delhi, Delhi, India for conducting this research. The third author would like to thank University Grants Commission for providing Junior Research Fellowship vide letter No. JRF/AA/168/2010-11, 47126.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML